2021-2022学年北师大版九年级数学下 册第三章 圆选择题与填空题培优专练(Word版含解析)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下 册第三章 圆选择题与填空题培优专练(Word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-04 23:33:18 | ||
图片预览



文档简介
北师大版九下第三章 圆选择题与填空题培优专练
一、单选题
1.(2021九上·哈尔滨月考)如图,四边形ABCD内接于 ,如果它的一个外角 ,那么 的度数为( )
A. 64° B. 128° C. 20° D. 116°
2.(2021九上·阳信期中)如图,AB是⊙O的直径,点D在AB的延长线上,DC切⊙O于点C,若∠A=25°,则∠D等于( )
A. 20° B. 30° C. 40° D. 50°
3.(2021九上·鄂尔多斯期中)已知矩形ABCD的边AB=15,BC=20,以点B为圆心作圆,使A,C,D三点至少有一点在⊙B内,且至少有一点在⊙B外,则⊙B的半径r的取值范围是( ).
A. r>15 B. 15<r<20 C. 15<r<25 D. 20<r<25
4.(2021九上·罗庄期中)如图, 的内切圆 与 分别相切于点D , E , F , 连接 , , , , ,则阴影部分的面积为( )
A. B. C. D.
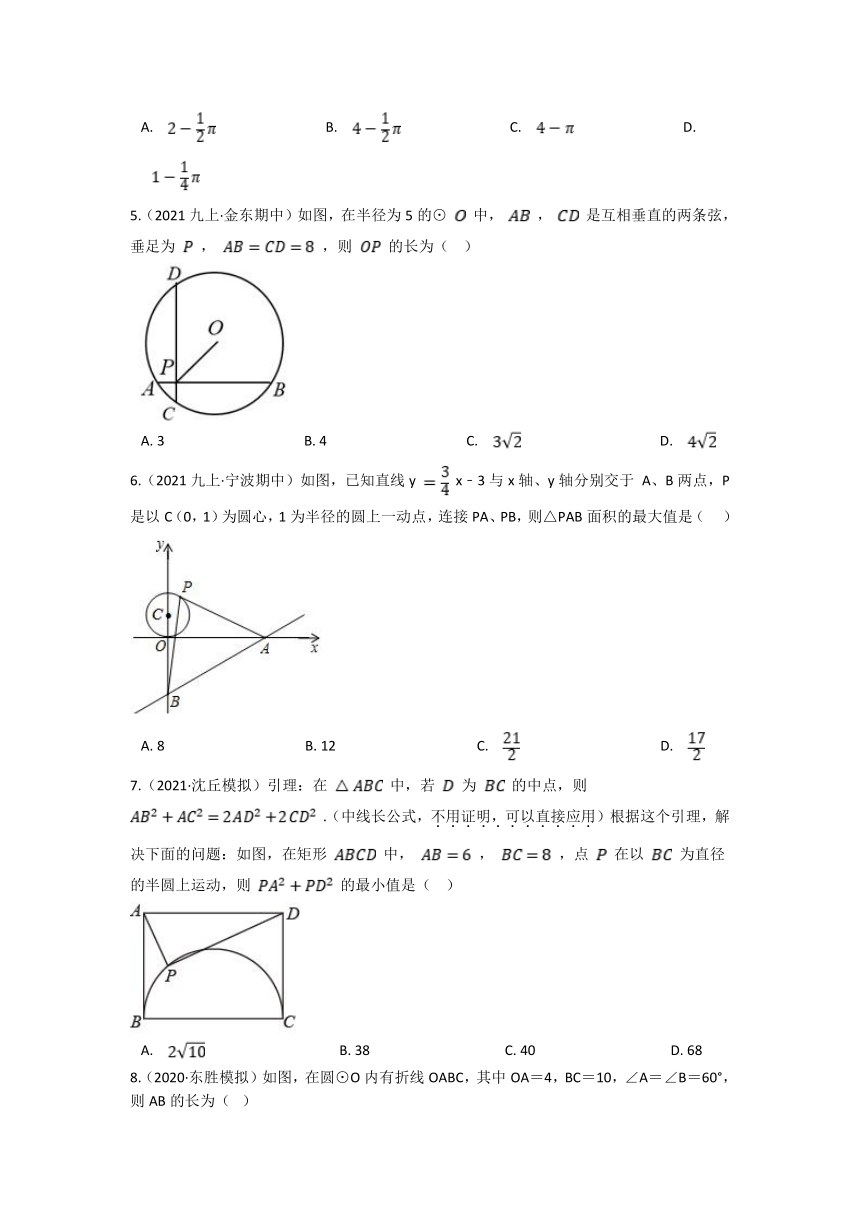
5.(2021九上·金东期中)如图,在半径为5的⊙ 中, , 是互相垂直的两条弦,垂足为 , ,则 的长为( )
A. 3 B. 4 C. D.
6.(2021九上·宁波期中)如图,已知直线y x﹣3与x轴、y轴分别交于 A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连接PA、PB,则△PAB面积的最大值是( )
A. 8 B. 12 C. D.
7.(2021·沈丘模拟)引理:在 中,若 为 的中点,则 .(中线长公式,不用证明,可以直接应用)根据这个引理,解决下面的问题:如图,在矩形 中, , ,点 在以 为直径的半圆上运动,则 的最小值是( )
A. B. 38 C. 40 D. 68
8.(2020·东胜模拟)如图,在圆⊙O内有折线OABC,其中OA=4,BC=10,∠A=∠B=60°,则AB的长为( )
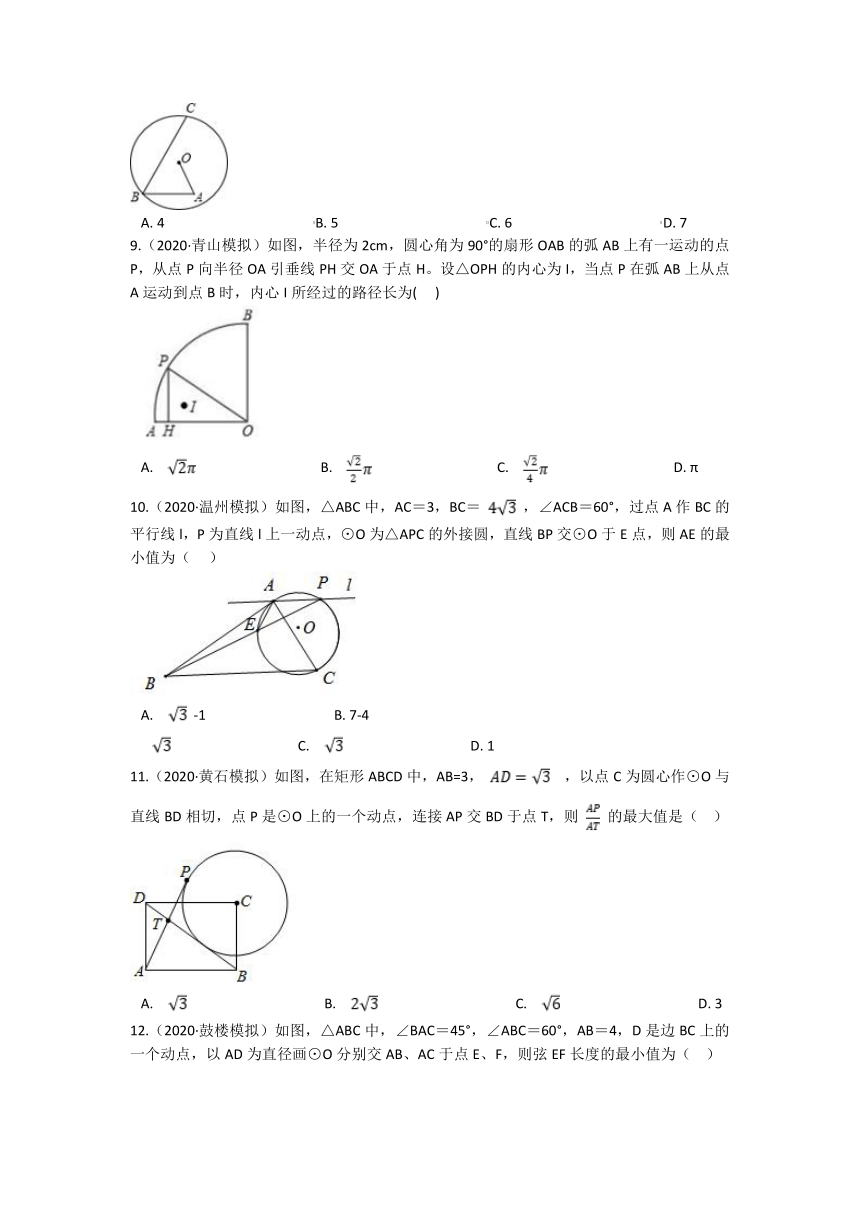
A. 4 B. 5 C. 6 D. 7
9.(2020·青山模拟)如图,半径为2cm,圆心角为90°的扇形OAB的弧AB上有一运动的点P,从点P向半径OA引垂线PH交OA于点H。设△OPH的内心为I,当点P在弧AB上从点A运动到点B时,内心I所经过的路径长为( )
A. B. C. D. π
10.(2020·温州模拟)如图,△ABC中,AC=3,BC= ,∠ACB=60°,过点A作BC的平行线l,P为直线l上一动点,⊙O为△APC的外接圆,直线BP交⊙O于E点,则AE的最小值为( )
A. -1 B. 7-4 C. D. 1
11.(2020·黄石模拟)如图,在矩形ABCD中,AB=3, ,以点C为圆心作⊙O与直线BD相切,点P是⊙O上的一个动点,连接AP交BD于点T,则 的最大值是( )
A. B. C. D. 3
12.(2020·鼓楼模拟)如图,△ABC中,∠BAC=45°,∠ABC=60°,AB=4,D是边BC上的一个动点,以AD为直径画⊙O分别交AB、AC于点E、F,则弦EF长度的最小值为( )
A. B. C. 2 D. 2
13.(2020九上·龙马潭期末)如图, 的直径 的长为 ,弦 长为 , 的平分线交 于D,则 长为( )
A. 7 B. 7 C. 8 D. 9
14.(2019九上·江都月考)如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0)直线y=kx-3k+4与 交于B、C两点,则弦BC的长的最小值为( )
A. 22 B. 24 C. D.
15.(2019九上·鼓楼月考)如图,已知直线 与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是( )
A. 8 B. 12 C. D.
16.(2019九上·无锡月考)如图,AB是⊙o直径,M,N是 上两点,C是 上任一点,∠ACB角平分线交⊙o于点D,∠BAC的平分线交CD于点E,当点C从M运动到N时,C、E两点的运动路径长之比为( )
A. B. C. D.
17.(2019·武汉模拟)如图,⊙O内切于正方形ABCD,边AD,CD分别与⊙O切于点E,F,点M、N分别在线段DE,DF上,且MN与⊙O相切,若△MBN的面积为8,则⊙O的半径为( )
A. B. 2 C. D. 2
18.以坐标原点O为圆心,作半径为2的圆,若直线y=﹣x+b与⊙O相交,则b的取值范围是( )
A. 0≤b<2 B. ﹣2 C. ﹣22 D. ﹣2 <b<2
19.如图,AB为⊙O的直径,C为⊙O上一点,其中AB=4,∠AOC=120°,P为⊙O上的动点,连AP,取AP中点Q,连CQ,则线段CQ的最大值为( )
A. 3 B. 1+ C. 1+3 D. 1+
20.如图,在△ABC中,AB=AC=10,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF= ∠A,tan∠CBF= , 则CF的长为
( )
A. B. C. D.
二、填空题
21.(2021九上·无棣期中)如图,已知圆O为 的内切圆,切点分别为D、E、F,且 , , ,则圆O的半径为 .
22.(2021九上·鹿城期中)如图, 为 的直径, 点 是弧 的中点, 过点 作 于点 , 延长 交 于点 , 若 , 则 的半径长为
23.(2021九上·衢州期中)如图,MN是⊙O的直径,MN=2,点A在⊙O上,∠AMN=40°,B为弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为 .
24.(2021九上·贵州期中)如图,△ABC内接于⊙O,∠ACB=90°,∠ACB的角平分线交⊙O于D。若AC=6,BD=5 ,则BC的长为 。
25.(2021九上·高港月考)如图,∠MON=45°,一直角三角尺△ABC的两个顶点C、A分别在OM,ON上移动,若AC=6,则点O到AC距离的最大值为 .
26.(2021九上·温州期中)如图,已知⊙O的内接四边形ABCD,AB是直径,点C是 的中点,连结AC,过点C作CE⊥AD,交AD的延长线于点E,过点D作DG⊥AB于点G,若△ABC的面积为5,△DEC的面积为1.
(1)△ACD的面积为 ;
(2)DG∶AB= .
27.(2021·阜宁模拟)如图,在直角坐称系中,半径为1的⊙A圆心A的坐标为(﹣1,0),点P为直线y=﹣ x+2上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是 .
28.(2021·岳阳模拟)如图, 内接于⊙O, 平分 交 边于点E,过点D作⊙O的切线,过点A作 于点F,设 ,⊙O的半径为R, 则下列结论正确的是 .(写出所有正确结论的序号)
① ;② ;③ ;④ .
29.(2020九上·嘉兴期中)如图,C、D是以AB为直径的圆O上的两个动点(点C、D不与A、B重合),在运动过程中弦CD始终保持不变,M是弦CD的中点,过点C作CP⊥AB于点P.若CD=3,AB=5,PM最大值是________.
30.(2020九上·麻章期中)如图,在平面直角坐标系中,⊙P的圆心是(4,a)且(a>2)半径为4,函数 的图像被⊙P截得的弦AB的长为 ,则a的值是 .
31.(2020九上·武汉月考)如图, 为 的直径,C为 上一动点,将 绕点A逆时针旋转120°得 ,若 ,则 的最大值为 .
32.(2020·潮南模拟)如图,AB是半圆O的直径,且AB=12,点C为半圆上的一点.将此半圆沿BC所在的直线折叠,若圆弧BC恰好过圆心O , 则图中阴影部分的面积是________ . (结果保留π)
33.(2020九上·长沙期末)如图, 是锐角 的外接圆, 是 的切线,切点为F, ,连结 交 于E, 的平分线 交 于D,连结 .下列结论:① 平分 ;②连接 ,点F为 的外心;③ ;④若点M,N分别是 和 上的动点,则 的最小值是 .其中一定正确的是________(把你认为正确结论的序号都填上).
34.(2020九上·龙马潭期末)如图, 内接于⊙O, ,D是⊙O上与点B关于圆心O成中心对称的点,P是 边上一点,连结 .已知 , ,Q是线段 上一动点,连结 并延长交四边形 的一边于点R,且满足 ,则 的值为________.
35.(2019·瑞安模拟)如图,已知AB为⊙O的直径,点C,E在⊙O上,且sin∠ACE= ,点D为弧BE中点,连结DE,则 的值为________.
36.(2019九上·哈尔滨月考)如图,已知AB是半圆的直径,且AB=10,弦AC=6,将半圆沿过点A的直线折叠,使点C落在直径AB上的点C′,则折痕AD的长为________.
37.(2019九下·成都开学考)如图,在矩形 中, , ,对角线 、 相交于点 ,现将一个直角三角板 的直角顶点与 重合,再绕着 点转动三角板,并过点 作 于点 ,连接 .在转动的过程中, 的最小值为________.
38.如图,AB是半圆O的直径,D是弧AB上一点,C是弧AD的中点,过点C作AB的垂线,交AB于E,与过点D的切线交于点G,连接AD,分别交CE、CB于点P、Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心.其中正确结论是________(填序号).
39.如图,在半径为5的⊙O中,弦AB=8,P是弦AB所对的优弧上的动点,连接AP,过点A作AP的垂线交射线PB于点C,当△PAB是等腰三角形时,线段BC的长为 .
40.如图,已知A,B两点的坐标分别为(2 ,0),(0,10),M是△AOB外接圆⊙C上的一点,且∠AOM=30°,则点M的坐标为 .
答案解析部分
一、单选题
1.【答案】 B
【解析】【解答】∵四边形ABCD内接于
∴∠BAD+∠DCB=180°
∵∠DCE+∠DCB=180°
∴∠BAD=∠DCE=64°
∵∠BOD、∠BAD对着圆中同一段弧
∴∠BOD=2∠BAD=2×64°=128°
故答案为:B
【分析】先求出∠BAD+∠DCB=180°,再求出∠BAD=∠DCE=64°,最后计算求解即可。
2.【答案】 C
【解析】【解答】解:连接OC,如下图:
∵ ,
∴
又∵DC切⊙O于点C,OC为半径
∴
∴ 是直角三角形
∴
∴
故答案为:C
【分析】连接OC,由于AB是直径,可知 , , 推出 是直角三角形,再利用三角形外角性质求解即可。
3.【答案】 C
【解析】【解答】要确定点与圆的位置关系,主要根据点与圆心的距离与半径的大小关系来进行判断.
当d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内.在直角△BCD中CD=AB=15,BC=20,则BD= = =25.由图可知15<r<25,
故答案为:C.
【分析】要确定点与圆的位置关系,主要根据点与圆心的距离与半径的大小关系来进行判断,当d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内.
4.【答案】 C
【解析】【解答】解:连接OD , 如图:
在 中, , , ,
由勾股定理,则
,
设半径为r , 则 ,
∴ ,
∴四边形CEOF是正方形;
由切线长定理,则 , ,
∵ ,
∴ ,
解得: ,
∴ ;
∴阴影部分的面积为: ;
故答案为:C .
【分析】连接OD , 设半径为r , 则 ,得出 ,四边形CEOF是正方形;由切线长定理,则 , ,列出方程解得出x的值即可得出答案。
5.【答案】 C
【解析】【解答】解:如图,连接 OA 过 作 垂足分别为 而
四边形 为矩形,
同理:
四边形 为正方形,
故答案为:C.
【分析】连接OA、OC,过O作OF⊥AB,OE⊥CD,垂足分别为F、E,则 四边形OEPF为矩形,由垂径定理可得AF=BF=4,结合勾股定理求出OF,同理可得OE,推出四边形OEPF为正方形,则FP=FO=3,然后由勾股定理可得OP的值.
6.【答案】 C
【解析】【解答】解:过C作CH⊥AB,延长HC交圆于P',连接AC、P'B、P'A,
当x=0时,y=-3,当y=0时,x=4,
∴A(0,-3),B(4,0),
∴AB==5,
∵BC=OB+OC=3+1=4,
∴S△ACB=BC×OA=AB×CH,
∴CH== ,
∴HP'=CH+HP'=+1= ,
∴ △PAB面积的最大值=S△P'AB=×AB×HP'=×5×= .
故答案为:C.
【分析】过C作CH⊥AB,延长HC交圆于P',连接AC、P'B、P'A, 则△PAB面积的最大值为S△P'AB ,
先求出直线AB与坐标轴交点的坐标,再利用勾股定理求出AB长,利用两点间坐标求出BC长,然后利用等积法求出CH长,则可求出HP',最后计算△P'AB的面积即可.
7.【答案】 C
【解析】【解答】解:如图,设AD中点为E,半圆圆心为O,连接OE,交半圆于P,此时PE取最小值,
∵四边形ABCD是矩形, , ,
∴AE=DE=4,OB=OC=OP=4,
∴CD=AB=OE=6,AD=BC=8,
∴PE=2,
∵点E为AD中点,
∴ =2PE2+2AE2 ,
∴ 的最小值为2PE2+2AE2=2×22+2×42=40,
故答案为:C.
【分析】设AD中点为E,半圆圆心为O,连接OE,交半圆于P,此时PE取最小值,由矩形的性质可得AE=DE,OB=OC=OP,于是由线段的构成PE=AB-OP可求得PE的值,由勾股定理可得PA2+PD2=2PE2+2AE2求解.
8.【答案】 C
【解析】【解答】延长AO交BC于点E,
∵
∴等边三角形ABE
过点O作OD BC于点D,在 中 ,
∴
设 , ,
又根据垂径定理得 ,
∵BE=AE
∴BD+DE=AO+OE
即 ,解得 ,
∴AB=BE=5+1=6.
故答案为:C.
【分析】延长AO交BC于点E,过点O作OD BC于点D,由 , 可得等边三角形ABE,设AB的长为x,由此可表示出OD、BD和DE的长;在 中 ,进而求的x的值。
9.【答案】 B
【解析】【解答】解:如图,连OI,PI,AI。
∵PH⊥OA
∴∠PHO=90°,
∴∠HOP+∠OPH=90°
又∵I为△OPH的内心
∴∠IOP=∠IOA=∠HOP,∠IPO=∠OPH
∴∠IOP+∠IPO=(∠HOP+∠OPH)=45°
∴∠PIO=180°-(∠IPO+∠IOP)=180°-45°=135°
又∵OP=OA,OI=OT,∠IOP=∠IOA
∴△OPI≌△OAI
∴∠AIO=∠PIO=135°
∴点I在以OA为弦,并且所对的圆周角为135°的一段劣弧上
过A、I、O三点作⊙O′,连O′A,O′O,在优弧AO取点P,连PA,PO。
∴∠APO=180°-∠AIO=180°-135°=45°
∴∠AO′O=90°
∴O′O=OA=×2=
∴弧OA的长=.
∴内心I所经过的路径长为。
故答案为:B.
【分析】连OI,PI,AI,先利用三角形的内心的定义求出∠PIO=135°,然后易证△OPI≌△OAI,利用相似三角形的对应角相等得到∠AIO=∠PIO=135°,所以点I在以OA为弦,并且所对的圆周角为135°的一段劣弧上;过A、I、O三点作⊙O′,连O′A,O′O,在优弧AO取点P,连PA,PO,利用圆内接四边形的性质可得∠APO=45°,进而得∠AOO=90°,则可求出O′O,然后利用弧长公式计算即可。
10.【答案】 D
【解析】【解答】解:如图,连接CE.
∵AP∥BC,
∴∠PAC=∠ACB=60°,
∴∠CEP=∠CAP=60°,
∴∠BEC=120°,
∴点E在以M为圆心,MB为半径的 上运动,
∴ 中优弧 度数为240°,劣弧 度数为120°
∴△BOC是等腰三角形,∠BOC=120°,
∵∠BCM=30°,BC= .
∴MB=MC=4,
∴连接MA交 于E′,此时AE′的值最小.
∵∠ACB=60°,∠BCO=30°,
∴∠ACM=90°,
∴MA= = ,
∴AE的最小值为=5-4=1.
故答案为:D.
【分析】如图,连接CE.首先证明∠BEC=120°,由此推出点E在以M为圆心,MB为半径的 上运动,连接MA交 于E′,此时AE′的值最小.
11.【答案】 D
【解析】【解答】解:如图,过点A作AG⊥BD于G点,
∵∠BAD=90°,
∴ ,
∵ ,
∴ ,
∴点C到BD的距离为 ,
∵BD是圆的切线,
∴圆的半径为 ,
过点P作PE⊥BD于点E,
∴∠AGT=∠PET,
∵∠ATG=∠PTE,
∴ ,
∴ ,
∴ ,
∵ ,
要使 最大,则 最大,即PE最大,
∵点P是圆上动点,BD是圆的切线,
∴PE最大为圆的直径,
即PE最大值为:3,
∴ 最大值为 ,
故答案为:D.
【分析】如图,过点A作AG⊥BD于G点,利用矩形的性质结合勾股定理求出BD,由此提高等面积法求得AG= ,从而得分析出圆的半径为 ,紧接着过点P作PE⊥BD于点E,提高证明 利用相似三角形性质得出 ,据此根据题意分析出要使 最大,则 最大,即PE最大,最后进一步分析求解即可.
12.【答案】 B
【解析】【解答】解:作AH⊥BC于H,OG⊥EF于G,连接OE、OF,如图,
∵∠EOF=2∠EAF=2×45°=90°,OE=OF,
而OE=OF,
∴EF= OE,
当OE的值最小时,EF的值最小,
此时AD最小,AD的最小值为AH的长,
在Rt△ABH中,
∵sin∠ABH==sin60°,
∴AH= ,
,∴OE的最小值为 ,
∴EF的最小值为 × = .
故答案为:B.
【分析】作AH⊥BC于H,OG⊥EF于G,连接OE、OF,如图,利用圆周角定理得∠EOF=90°,利用含30度的直角三角形三边的关系得到EF=2EG= OE,所以当⊙O的半径最小时,EF的值最小,此时AD最小,AD的最小值为AH的长,然后计算出AH的长就可得到EF的最小值.
13.【答案】 B
【解析】【解答】解:作DF⊥CA,垂足F在CA的延长线上,作DG⊥CB于点G,连接DA,DB,
∵CD平分∠ACB,
∴∠ACD=∠BCD
∴DF=DG, ,
∴DA=DB,
∵∠AFD=∠BGD=90°,
∴△AFD≌△BGD,
∴AF=BG.
易证△CDF≌△CDG,
∴CF=CG,
∵AC=6,BC=8,
∴AF=1,
∴CF=7,
∵△CDF是等腰直角三角形,
∴CD=7 ,
故答案为:B.
【分析】作DF⊥CA,交CA的延长线于点F,作DG⊥CB于点G,连接DA,DB.由CD平分∠ACB,根据角平分线的性质得出DF=DG,由HL证明△AFD≌△BGD,△CDF≌△CDG,得出CF=7,又△CDF是等腰直角三角形,从而求出CD=7 .
14.【答案】 B
【解析】【解答】根据题意可得直线经过定点D(3,4),则OD=5,当OD⊥BC时,BC取得最小值,根据垂径定理可得BC=24.
【分析】根据直线经过定点D(3,4),求出最短的弦BC是过点D且该圆直径垂直的弦,再求出OD的长,再根据以原点O为圆心过点A(13,0 ),求出OB的长,然后利用勾股定理求出BD即可.
15.【答案】 C
【解析】【解答】解:∵直线 与x轴、y轴分别交于A、B两点,
∴A点的坐标为(4,0),B点的坐标为(0,﹣3),
,即OA=4,OB=3,
由勾股定理得:AB=5,
过C作CM⊥AB于M,连接AC,
则由三角形面积公式得: ×AB×CM= ×OA×OC+ ×OA×OB,
∴5×CM=4×1+3×4,
∴CM= ,
∴圆C上点到直线 的最大距离是 = ,
∴△PAB面积的最大值是 = ,
故答案为:C.
【分析】求出A、B的坐标,根据勾股定理求出AB,求出点C到AB的距离,即可求出圆C上点到AB的最大距离,根据面积公式求出即可.
16.【答案】 A
【解析】【解答】如图,连接EB,设
∵AB是直径
∵E是 的内心,
∴点E在以D为圆心DA为半径的圆上,运动轨迹是 ,点C的运动轨迹是
∵ ,设 ,则 ,
故答案为:A
【分析】如图,连接EB,设 ,易知点E在以D为圆心DA为半径的圆上,运动轨迹是 ,点C的运动轨迹是 ,由题意 ,设 ,则 ,利用弧长公式计算后即可解决问题.
17.【答案】 B
【解析】【解答】解:设⊙O与MN相切于点K,设正方形的边长为2a.
∵AD、CD、MN是切线,
∴AE=DE=DF=CF=a,MK=ME,NK=NF,设MK=ME=x,NK=NF=y,
在Rt△DMN中,∵MN=x+y,DN=a﹣y,DM=a﹣x,
∴(x+y)2=(a﹣y)2+(a﹣x)2 ,
∴ax+ay+xy=a2 ,
∵S△BMN=S正方形ABCD﹣S△ABM﹣S△DMN﹣S△BCN=8,
∴4a2﹣ ×2a×(a+x)﹣ (a﹣x)(a﹣y)﹣ ×2a×(a+y)=8,
∴ a2﹣ (ax+ay+xy)=8,
∴a2=8,
∴a=2 ,
∴AB=2a=4 ,
∴⊙O的半径为2 ,
故答案为:B.
【分析】设⊙O与MN相切于点K,设正方形的边长为2a.因为AD、CD、MN是切线,可得AE=DE=DF=CF=a,MK=ME,NK=NF,设MK=ME=x,NK=NF=y,在Rt△DMN中,以为MN=x+y,DN=a-y,DM=a-x,看到(x+y)2=(a-y)2+(a-x)2 , 推出ax+ay+xy=a2 , 根据S△BMN=S正方形ABCD-S△ABM-S△DMN-S△BCN=8,构建方程求出a即可解决问题;
18.【答案】 D
【解析】【解答】解: 当直线y=﹣x+b与圆相切,且函数经过一、二、四象限时,如图.
在y=﹣x+b中,令x=0时,y=b,则与y轴的交点是(0,b),
当y=0时,x=b,则A的交点是(b,0),
则OA=OB,即△OAB是等腰直角三角形.
连接圆心O和切点C.则OC=2.
则OB= OC=2 .即b=2 ;
同理,当直线y=﹣x+b与圆相切,且函数经过二、三、四象限时,b=﹣2 .
则若直线y=﹣x+b与⊙O相交,则b的取值范围是﹣2 <b<2 .
故答案为:D.
【分析】求出直线y=-x+b与圆相切,且函数经过的象限分别求出此时b的值,则相交时b的值在相切时的两个b的值之间.
19.【答案】 D
【解析】【解答】解:如图,连接OQ,作CH⊥AB于H.
∵AQ=QP,
∴OQ⊥PA,
∴∠AQO=90°,
∴点Q的运动轨迹为以AO为直径的⊙K,连接CK,
当点Q在CK的延长线上时,CQ的值最大,
在Rt△OCH中,∵∠COH=60°,OC=2,
∴OH= OC=1,CH= ,
在Rt△CKH中,CK= = ,
∴CQ的最大值为1+ ,
故答案为:D.
【分析】如图,连接OQ,作CH⊥AB于H,根据垂径定理可得OQ⊥PA,即得∠AQO=90°,从而可判断点Q的运动轨迹为以AO为直径的⊙K,连接CK,可得当点Q在CK的延长线上时,CQ的值最大.在Rt△OCH中,利用直角三角形的性质可求出OH、CH的长,在Rt△CKH中利用勾股定理求出CK的长,从而求出CQ的长.
20.【答案】 A
【解析】【解答】∵AB为直径,
∴AE⊥BC,
∵AB=AC,
∴∠EAB=BAC,=∠CBF,
EB=CE=CB,
∴∠CBF=∠EAB,tan∠EAB== ,
∴∠CBF+∠ABC=∠EAB+∠ABC=90°,
∴FB是⊙O的切线,
∴FB2=FD FA,
在RT△AEB中,AB=10,
∴EB= ,
∴CB=2 , CE=,
∵CE CB=CD AC,AC=10,
∴CD=2,
∴AD=AC-CD=8,
设CF=x,则FD=x+2,FA=10+x,FB2=AF2-AB2=(10+x)2-102,
∴(10+x)2-102=(x+2)(10+x),
整理得:x= ,
∴CF= ,
答案为;A
【分析】连接AE,根据AB是直径,得出AE⊥BC,CE=EB,依据已知条件得出∠CBF=∠EAB,BF是圆的切线,进而得出BC的长,然后根据割线定理求得CD的长,最后根据切割线定理求得FC
二、填空题
21.【答案】 2
【解析】【解答】如图,连接OA、OB、OC、OD、OE、OF
∵⊙O为 的内切圆,切点分别为D、E、F
∴OD⊥AB,OE⊥AC,OF⊥BC,且OD=OE=OF
在Rt△ABC中,由勾股定理得
∴
∵
∴
即
∴OD=2
即⊙O的半径为2
故答案为:2
【分析】利用勾股求出AC,然后利用 , 得到关于半径的方程,求解即可得出答案。
22.【答案】
【解析】【解答】解:如图,连接OF.
∵DE⊥AB,
∴DE=EF, ,
∵点D是弧AC的中点
∴ ,
∴ ,
∴AC=DF=12,
∴EF= DF=6,设OA=OF=x,
在Rt△OEF中,则有x2=62+(x-3)2 ,
解得x= .
故答案为:.
【分析】连接OF,由垂径定理可得DE=EF, , 根据点D是弧AC的中点可得 , 推出 , 根据等弧所对的弦相等得AC=DF=12,由垂径定理可得EF,设OA=OF=x,然后在Rt△OEF中,应用勾股定理求解即可.
23.【答案】
【解析】【解答】解:作点B关于MN的对称点C,连接AC交MN于点P,则P点就是所求作的点.
此时PA+PB最小,且等于AC的长.
连接OA,OC,OB,作OD⊥AC于D,
∵∠AMN=40°,
∴∠AON=80°,
∵B为弧AN的中点,
∴∠AOB=∠NOB=40°,
由对称可知,∠CON=∠NOB=40°,
∴∠AOC=120°,
∵MN=2
∴OA=OC=1,
∴∠OAC=∠OCA=30°,
∴OD= ,
,
AC=2CD= .
故答案为: .
【分析】作点B关于MN的对称点C,连接AC交MN于点P,此时PA+PB最小,且等于AC的长,连接OA,OC,OB,作OD⊥AC于D,由圆周角定理可得∠AON=2∠AMN=80°,根据中点的概念可得∠AOB=∠NOB=40°,由对称可知:∠CON=∠NOB=40°,则∠AOC=120°,易得OA=OC=1,然后求出OD、CD,进而可得AC.
24.【答案】 8
【解析】【解答】解:如图,连接AD,
∵AB为直径,
∴∠ACB=∠ADB=90°,
∵CD为∠ACB的角平分线,
∴∠BCD=45°,
∴∠BAD=∠BCD=45°,
∴AB=BD= 5 ,
∴BC==8.
故答案为:8.
【分析】连接AD,由圆周角定理得出∠ACB=∠ADB=90°,然后由根据角平分线的定义求出∠BCD=45°,再由同弧所对的圆周角定理求出∠BAD=45°,则由等腰直角三角形的性质求出AB长,最后由勾股定理求BC长即可.
25.【答案】 3 +3
【解析】【解答】解:如图,作△AOC的外接圆⊙P,过点P作PQ⊥AC与Q,延长QP⊙P于O',连接PA、PC.
当点O在圆周上运动到点O',即点O与O'重合时,点O到AC距离最大.
∵∠MON=45°,
∴∠CO'A=45°,
∴∠CPA=90°,
∵PQ⊥AC,
∴QA=QC= AC=3,
∴PQ= AC=3,
PA= QA=3 ,
OP=AP=3 ,
∴O'Q=OP+PQ=3 +3.
故答案为:3 +3.
【分析】作△AOC的外接圆⊙P,过点P作PQ⊥AC与Q,延长QP⊙P于O',连接PA、PC;由题意知:当点O在圆周上运动到点O',即点O与O'重合时,点O到AC距离最大。根据O'Q=OP+PQ可求解.
26.【答案】 (1)3
(2)12:25
【解析】【解答】解:过点C作CF⊥AB于点F,
∵点C是弧DB的中点
∴弧CD=弧BC,
∴∠DAC=∠BAC,CD=BC
∴AC平分∠DAB,
∵CE⊥CD,
∴FC=CE,
在Rt△DEC和R△BFC中
∴Rt△DEC≌R△BFC(HL)
同理可证△AEC≌△ACF
∴S△DEC=S△BFC=1,S△AEC=S△ACF ,
∵S△ABC=S△ACF+S△BFC=5
∴S△AEC=S△ACF=5-1=4,
∴S△ADC=S△AEC-S△DEC=4-1=3.
故答案为:3.
(2)连接OC,BD交于点H,
∵
∴DA=3DE,
设DE=a,则DA=3a,
∵AB是圆的直径,
∴∠ADB=∠EDH=90°=∠E,
∵点C是弧BD的中点,
∴OC⊥BD
∴∠DHC=90°,
∴四边形DEHC是矩形,
∴CH=DE=a,
OH是△ADB的中位线
∴
∴OC=CH+OH=a+=
∴AB=2OC=5a,
∴ ,
∵
∴5a·DG=3a·4a
解之:DG=2.4a
∴DG∶AB=2.4a:5a=12:25.
故答案为:12:25.
【分析】 (1)过点C作CF⊥AB于点F,利用弧的中点及等弧所对圆周角相等,可知AC平分∠DAB,CD=BC,利用角平分线的性质可得到FC=CE;利用HL可证得Rt△DEC≌R△BFC,△AEC≌△ACF,利用全等三角形的面积相等可推出S△DEC=S△BFC=1,S△AEC=S△ACF , 从而可求出△AEC的面积及△ACD的面积.
(2)连接OC,BD交于点H,利用△CDE和△ADC的面积可证得DA=3DE,设DE=a,则DA=3a;利用直径所对圆周角是直角,可证得∠ADB=∠EDH=90°=∠E,利用垂径定理可证得∠DHC=90°,由此可推出四边形DEHC是矩形,可得到CH=a,利用三角形的中位线定理可求出OH的长,即可表示出圆的半径,再表示出圆的直径AB的长;再利用勾股定理求出BD的长,利用直角三角形的两个面积公式可表示出DG的长;然后求出DG∶AB的值.
27.【答案】 2
【解析】【解答】解:过点P作⊙A的切线,切点为Q,连接AP、AQ,设直线 与x、y轴的交点分别为B、C,如图所示:
∴∠AQP=90°,
令y=0时,则 ,解得 ,令x=0时,则y=2,
∴OC=2,OB=4,
∵半径为1的⊙A圆心A的坐标为(﹣1,0),
∴ ,
∴AB=5,
∴在Rt△PQA中, ,
∴当切线长PQ为最小时,则AP为最小,由此可得当AP与直线 垂直时AP取最小,连接AC,则由勾股定理可得 ,
∴ ,
∴AC⊥BC,
∴当点P与点C重合时,PQ取最小值,如图所示,
∵OA=AQ,AC=AC,∠AQP=∠AOP=90°,
∴△AQP≌△AOP(HL),
∴OP=PQ=2,
∴PQ的最小值为2;
故答案为2.
【分析】过点P作⊙A的切线,切点为Q,连接AP、AQ,设直线 与x、y轴的交点分别为B、C,可得∠AQP=90°,利用勾股定理可得 , 可知当AP最小时,PQ最小,根垂线段最短,可知当AP⊥BC时,AP最小,此时当点P与点C重合时,证明Rt△AQP≌Rt△AOP,可得OP=PQ=2,据此即得结论.
28.【答案】 ①③④
【解析】【解答】解:①连接 ,如图,
∵ 平分 ,
∴ .
∴ ,
∴ .
∵ 为⊙O的切线,
∴ .
∴MN∥BC,所以①正确;
②∵
∴∠DBC=∠CAD.
∴ .
∴只有当 或∠BED=∠BAC时,
而上述的条件不具备,所以②错误;
③过A点作直径 ,连接BG,如图,
∵ 为直径,
∴ .
∵ ,
∴ .
∴ .
∵
.
∴ .
∴ .
. 所以③正确;
④过D点作 于P, 交AC的延长线于点Q,连接DC.如图,
∵ 平分 ,
∴ , .
∴
∴ .
在 中, ,
∴ .
同理,在 中, .
在 和 中,
,
∴ .
∴ ,
即 .
∴ .
∴ .所以④正确.
故答案为:①③④.
【分析】连接OD,由角平分线的概念可得∠BAD=∠CAD,推出OD⊥BC,由切线的性质可得OD⊥MN,据此可判断①;由圆周角定理可得∠DBC=∠CAD,推出∠DBC=∠BAD,然后根据相似三角形的判定定理可判断②;过A点作直径AG,连接BG,由圆周角定理可得∠ABG=90°,由垂直的概念可得∠AFC=90°,证明△ABG∽△AFC,由相似三角形的性质可判断③;过D点作DP⊥AB于P, DQ⊥AC交AC的延长线于点Q,连接DC,易得∠BAD=∠QAD=α,DP=DQ,DB=DC,证明△DBP≌△DCQ,得到BP=CQ,即AB-AP=AQ-AC,据此判断④.
29.【答案】 2.5
【解析】【解答】解:当CD∥AB时,PM最长,连接OM,CO,
∵CD∥AB,CP⊥CD,
∴CP⊥AB
∵点M是CD的中点,OM过点O
∴OM⊥CD,
∴∠OMC=∠PCD=∠CPO=90°,
∴四边形CPOM是矩形,
∴PM=OC,
OC=AB=2.5
∴PM=2.5.
故答案为:2.5
【分析】当CD∥AB时,PM最长,连接OM,CO,利用垂径定理易证OM⊥CD,再证明∠OMC=∠PCD=∠CPO=90°,可推出四边形CPOM是矩形,利用矩形的对角线相等,可证得PM=OC,从而可求出PM的长。
30.【答案】
【解析】【解答】解:如图:过P点作PE⊥AB于E,过P点作PC⊥x轴于C,交AB于D,连接PA.
∵PE⊥AB,AB=4 ,半径为4,
∴AE= AB=2 ,PA=4,
根据勾股定理得:PE= ,
∵点A在直线y=x上,∴∠AOC=45°,
∵∠DCO=90°,∴∠ODC=45°,
∴△OCD是等腰直角三角形,∴OC=CD=4,
∴∠PDE=∠ODC=45°,∴∠DPE=∠PDE=45°,
∴DE=PE=2,∴PD=2 ∵⊙P的圆心是(4,a),
∴a=PD+DC=4+2 .
故答案为4+2
【分析】先求出AE= AB=2 ,PA=4,再求出PD=2 , 最后计算求解即可。
31.【答案】
【解析】【解答】解:将△ABD绕点A顺时针旋转120°,则D与点C重合,B′是定点,
BD的最大值即B′C的最大值,当B′,O,C三点共线时,BD最大
过点B′作B′E⊥AB,交BA的延长线于点E
由题意可得A′B=AB=4,∠EAB′=60°
∴AE=2,B′E= ,OC=OB=2
在Rt△OEB′中,B′O=
∴B′D= B′O+OC= .
故答案为: .
【分析】将△ABD绕点A顺时针旋转120°,则D与点C重合,B′是定点,BD的最大值即B′C的最大值,过点B′作B′E⊥AB,交BA的延长线于点E,由题意可得A′B=AB=4,∠EAB′=60°,求出AE、B′E、OC的值,在Rt△OEB′中,应用勾股定理求出B′O,据此求解.
32.【答案】 6π
【解析】【解答】
做出辅助线,如图所示,在Rt三角形BOD中, OB=R=6,OD=3
所以∠OBD=30°,∠AOC=60°,
∴阴影部分面积对应的圆心角为60°,代入公式可得
【分析】根据直角三角形的性质可得出角的度数的关系,利用扇形面积公式可得出阴影部分面积。
33.【答案】
【解析】【解答】解:如图 ,连接 ,
∵ 是 的切线,
∴ ,∵
∴ ,且 为半径
∴ 垂直平分
∴
∴
∴ 平分 ,故 符合题意
点 的外心,故 符合题意;
如图 ,过点C作 交 的延长线与点G
,故 符合题意;
如图 ,作点M关于 的对称点 ,
点M与点 关于 对称,
当点N在线段 上,且 时, ,
且
∴ 的最小值为 ;故 符合题意.
故答案为: .
【分析】如图1,连接 ,通过切线的性质证 ,进而由 ,即可由垂径定理得到F是 的中点,根据圆周角定理可得 ,可得 平分 ;由三角形的外角性质和同弧所对的圆周角相等可得 ,可得 ,可得点F为 得外心;如图 2 ,过点C作 交 的延长线与点G通过证明 ,可得 ;如图 3 ,作点M关于 的对称点 ,当点N在线段 上,且 时, .
34.【答案】 1或
【解析】【解答】解:因为 内接于圆, ,D是⊙O上与点B关于圆心O成中心对称的点,
∴AB=BC=CD=AD,
是正方形
①点R在线段AD上,
∵AD∥BC,
∴∠ARB=∠PBR,∠RAQ=∠APB,
∵AP=BR,
∴△BAP≌ABR,
∴AR=BP,
在△AQR与△PQB中,
,
②点R在线段CD上,此时△ABP≌△BCR,
∴∠BAP=∠CBR.
∵∠CBR+∠ABR=90°,
∴∠BAP+∠ABR=90°,
∴BQ是直角△ABP斜边上的高,
∴QR=BR-BQ=5-2.4=2.6,
.
故答案为:1或 .
【分析】首先证明四边形ABCD为正方形,即可得到AD∥BC,根据题意,由R点的位置,判断得到答案即可。
35.【答案】
【解析】【解答】解:连接OD,BD,AD,AE,BE,
∴∠ACE=∠ABE,
∵sin∠ACE= ,
∴sin∠ABE= = ,
∴设AE= x,AB=5x,
∴BE= =2 x,
∵点D为弧BE中点,
∴OD⊥BE,OD平分BE,
设OD,BE相交于H,
∴BH=EH= x,
∴OH= = x2 ,
∴DH= x2 ,
∵∠BAD=∠DBH,∠ADB=∠BHD=90°,
∴△BDH∽△ABD,
∴ ,
∴ = = ,
∴BD2= x,
∴AD2= x,
∵点D为弧BE中点,
∴BD=DE,
∴ = = ,
故答案为: .
【分析】连接OD,BD,AD,AE,BE,得到∠ACE=∠ABE,求得sin∠ABE= =
, 设AE= x,AB=5x,根据勾股定理得到BE= =2 x,根据垂径定理得到OD⊥BE,OD平分BE,设OD,BE相交于H,得到BH=EH= x,根据勾股定理得到OH= = x,求得DH= x,根据相似三角形的性质即可得到结论.
36.【答案】 .
【解析】【解答】
设圆的圆心是O,连接OD,作DE⊥AB于E,OF⊥AC于F.
根据题意知,∵OF⊥AC,∴AF= AC=3,
∵∠CAD=∠BAD,∴ ,∴点D是弧BC的中点.∴∠DOB=∠OAC=2∠BAD,
在△AOF和△OED中,∵∠OFA=∠OED,∠FAO=∠EDO,AO=DO,
∴△AOF≌△OED(AAS),∴OE=AF=3,
∵DO=5,∴DE=4,∴AD= .
故答案为 .
【分析】通过作辅助线,结合三角形全等的性质与判定,利用勾股定理求出线段的长度即可.
37.【答案】
【解析】【解答】解:∵∠OHD=90°,∴点H的运动轨迹为以OD为直径的圆上,
∵AB=4,BC=4 , ∴AC=BD=8, ∴AO=OD=4,
设OD的中点为M,则圆M的半径为2,∴AM= ,
当A、H、M三点在同一条直线上时,AH最短,则AH= .
【分析】首先根据∠OHD=90°得出点H的运动轨迹,根据直角三角形的勾股定理得出AO和OD的长度,设OD的中点为M,根据Rt△AOM的勾股定理得出AM的长度,从而得出最小值.
38.【答案】 ②③
【解析】【解答】∵在 中,AB是直径,点D是 上一点,点C是 的中点,
故①错误;
连接OD,
则OD⊥GD,∠OAD=∠ODA,
∴∠GPD=∠GDP;
∴GP=GD,故②正确;
∵弦CE⊥AB于点F,
∴A为 的中点,即
又∵C为 的中点,
∴∠CAP=∠ACP,
∴AP=CP.
∵AB为 的直径,
∴∠PCQ=∠PQC,
∴PC=PQ,
∴AP=PQ,即P为Rt△ACQ斜边AQ的中点,
∴P为Rt△ACQ的外心,故③正确;
故答案为:②③.
【分析】①由等弧所对圆周角相等可得两角相等,但弧BD与弧CD不一定相等,故①错误;②连接OD,结合切线的定义及GE⊥AB即可利用等角的余角相等证得∠GPD=∠GDP,再利用等角对等边即可得证 GP=GD ;③证P为Rt△ACQ的外心即证点P到三角形三个顶点的距离相等,又因为∠ACB是直径AB所对的圆周角,故∠ACB=90° ,即三角形ACQ为直角三角形,故只需证点P为其斜边AQ的中点即可.
39.【答案】 8, ,
【解析】【解答】解:①当BA=BP时,
易得AB=BP=BC=8,即线段BC的长为8.
②当AB=AP时,如图1,延长AO交PB于点D,过点O作OE⊥AB于点E,则AD⊥PB,AE=AB=4,
∴BD=DP,
在Rt△AEO中,AE=4,AO=5,
∴OE=3,
易得△AOE∽△ABD,
∴= ,
∴BD= ,
∴BD=PD= , 即PB= ,
∵AB=AP=8,
∴∠ABD=∠P,
∵∠PAC=∠ADB=90°,
∴△ABD∽△CPA,
∴= ,
∴CP= ,
∴BC=CP﹣BP=-=;
③当PA=PB时
如图2,连接PO并延长,交AB于点F,过点C作CG⊥AB,交AB的延长线于点G,连接OB,
则PF⊥AB,
∴AF=FB=4,
在Rt△OFB中,OB=5,FB=4,
∴OF=3,
∴FP=8,
易得△PFB∽△CGB,
∴== ,
设BG=t,则CG=2t,
易得∠PAF=∠ACG,
∵∠AFP=∠AGC=90°,
∴△APF∽△CAG,
∴= ,
∴= , 解得t= ,
在Rt△BCG中,BC=t= ,
综上所述,当△PAB是等腰三角形时,线段BC的长为8, , ,
故答案为:8, , .
【分析】①当BA=BP时,利用直角三角形斜边的中线等于斜边的一半;
②当AB=AP时,如图1,延长AO交PB于点D,过点O作OE⊥AB于点E,易得△AOE∽△ABD,利用相似三角形的性质求得BD,PB,然后利用相似三角形的判定定理△ABD∽△CPA,代入数据得出结果;
③当PA=PB时,如图2,连接PO并延长,交AB于点F,过点C作CG⊥AB,交AB的延长线于点G,连接OB,则PF⊥AB,易得AF=FB=4,利用勾股定理得OF=3,FP=8,易得△PFB∽△CGB,利用相似三角形的性质=, 设BG=t,则CG=2t,利用相似三角形的判定定理得△APF∽△CAG,利用相似三角形的性质得比例关系解得t,在Rt△BCG中,得BC.
40.【答案】 (4 ,4).
【解析】【解答】∵A,B两点的坐标分别为(2 ,0),(0,10),
∴OB=10,OA=2 ,
∴AB= =4 ,
∵∠AOB=90°,
∴AB是直径,CM=2 ,
∴Rt△AOB外接圆的圆心为AB中点,
∴C点坐标为( ,5),
过点C作CF∥OA,过点M作ME⊥OA于E交CF于F,作CN⊥OE于N,如图所示:
则ON=AN= OA= ,
设ME=x,
∵∠AOM=30°,
∴OE= x
∴∠CFM=90°,
∴MF=5﹣x,CF= x﹣ ,CM=2 ,
在△CMF中,根据勾股定理得:( x﹣ )2+(5﹣x)2=(2 )2 ,
解得:x=4或x=0(舍去),
∴OE= x=4
故答案为:(4 ,4).
【分析】过点C作CF∥OA,过点M作ME⊥OA于E交CF于F,作CN⊥OE于N;由圆周角性质易得直径AB=2;A,B两点的坐标分别为(2 ,0),(0,10)结合AB的中点O利用中位线易得C点坐标为( ,5),设ME=x,则利用前面所给条件可得MF=5﹣x,CF= x﹣ ,CM=2 ;在Rt△CFM中利用勾股定理可列方程( x﹣ )2+(5﹣x)2=(2 )2 , 解得ME=4,从而得到点M的坐标(4 ,4)。
一、单选题
1.(2021九上·哈尔滨月考)如图,四边形ABCD内接于 ,如果它的一个外角 ,那么 的度数为( )
A. 64° B. 128° C. 20° D. 116°
2.(2021九上·阳信期中)如图,AB是⊙O的直径,点D在AB的延长线上,DC切⊙O于点C,若∠A=25°,则∠D等于( )
A. 20° B. 30° C. 40° D. 50°
3.(2021九上·鄂尔多斯期中)已知矩形ABCD的边AB=15,BC=20,以点B为圆心作圆,使A,C,D三点至少有一点在⊙B内,且至少有一点在⊙B外,则⊙B的半径r的取值范围是( ).
A. r>15 B. 15<r<20 C. 15<r<25 D. 20<r<25
4.(2021九上·罗庄期中)如图, 的内切圆 与 分别相切于点D , E , F , 连接 , , , , ,则阴影部分的面积为( )
A. B. C. D.
5.(2021九上·金东期中)如图,在半径为5的⊙ 中, , 是互相垂直的两条弦,垂足为 , ,则 的长为( )
A. 3 B. 4 C. D.
6.(2021九上·宁波期中)如图,已知直线y x﹣3与x轴、y轴分别交于 A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连接PA、PB,则△PAB面积的最大值是( )
A. 8 B. 12 C. D.
7.(2021·沈丘模拟)引理:在 中,若 为 的中点,则 .(中线长公式,不用证明,可以直接应用)根据这个引理,解决下面的问题:如图,在矩形 中, , ,点 在以 为直径的半圆上运动,则 的最小值是( )
A. B. 38 C. 40 D. 68
8.(2020·东胜模拟)如图,在圆⊙O内有折线OABC,其中OA=4,BC=10,∠A=∠B=60°,则AB的长为( )
A. 4 B. 5 C. 6 D. 7
9.(2020·青山模拟)如图,半径为2cm,圆心角为90°的扇形OAB的弧AB上有一运动的点P,从点P向半径OA引垂线PH交OA于点H。设△OPH的内心为I,当点P在弧AB上从点A运动到点B时,内心I所经过的路径长为( )
A. B. C. D. π
10.(2020·温州模拟)如图,△ABC中,AC=3,BC= ,∠ACB=60°,过点A作BC的平行线l,P为直线l上一动点,⊙O为△APC的外接圆,直线BP交⊙O于E点,则AE的最小值为( )
A. -1 B. 7-4 C. D. 1
11.(2020·黄石模拟)如图,在矩形ABCD中,AB=3, ,以点C为圆心作⊙O与直线BD相切,点P是⊙O上的一个动点,连接AP交BD于点T,则 的最大值是( )
A. B. C. D. 3
12.(2020·鼓楼模拟)如图,△ABC中,∠BAC=45°,∠ABC=60°,AB=4,D是边BC上的一个动点,以AD为直径画⊙O分别交AB、AC于点E、F,则弦EF长度的最小值为( )
A. B. C. 2 D. 2
13.(2020九上·龙马潭期末)如图, 的直径 的长为 ,弦 长为 , 的平分线交 于D,则 长为( )
A. 7 B. 7 C. 8 D. 9
14.(2019九上·江都月考)如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0)直线y=kx-3k+4与 交于B、C两点,则弦BC的长的最小值为( )
A. 22 B. 24 C. D.
15.(2019九上·鼓楼月考)如图,已知直线 与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是( )
A. 8 B. 12 C. D.
16.(2019九上·无锡月考)如图,AB是⊙o直径,M,N是 上两点,C是 上任一点,∠ACB角平分线交⊙o于点D,∠BAC的平分线交CD于点E,当点C从M运动到N时,C、E两点的运动路径长之比为( )
A. B. C. D.
17.(2019·武汉模拟)如图,⊙O内切于正方形ABCD,边AD,CD分别与⊙O切于点E,F,点M、N分别在线段DE,DF上,且MN与⊙O相切,若△MBN的面积为8,则⊙O的半径为( )
A. B. 2 C. D. 2
18.以坐标原点O为圆心,作半径为2的圆,若直线y=﹣x+b与⊙O相交,则b的取值范围是( )
A. 0≤b<2 B. ﹣2 C. ﹣22 D. ﹣2 <b<2
19.如图,AB为⊙O的直径,C为⊙O上一点,其中AB=4,∠AOC=120°,P为⊙O上的动点,连AP,取AP中点Q,连CQ,则线段CQ的最大值为( )
A. 3 B. 1+ C. 1+3 D. 1+
20.如图,在△ABC中,AB=AC=10,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF= ∠A,tan∠CBF= , 则CF的长为
( )
A. B. C. D.
二、填空题
21.(2021九上·无棣期中)如图,已知圆O为 的内切圆,切点分别为D、E、F,且 , , ,则圆O的半径为 .
22.(2021九上·鹿城期中)如图, 为 的直径, 点 是弧 的中点, 过点 作 于点 , 延长 交 于点 , 若 , 则 的半径长为
23.(2021九上·衢州期中)如图,MN是⊙O的直径,MN=2,点A在⊙O上,∠AMN=40°,B为弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为 .
24.(2021九上·贵州期中)如图,△ABC内接于⊙O,∠ACB=90°,∠ACB的角平分线交⊙O于D。若AC=6,BD=5 ,则BC的长为 。
25.(2021九上·高港月考)如图,∠MON=45°,一直角三角尺△ABC的两个顶点C、A分别在OM,ON上移动,若AC=6,则点O到AC距离的最大值为 .
26.(2021九上·温州期中)如图,已知⊙O的内接四边形ABCD,AB是直径,点C是 的中点,连结AC,过点C作CE⊥AD,交AD的延长线于点E,过点D作DG⊥AB于点G,若△ABC的面积为5,△DEC的面积为1.
(1)△ACD的面积为 ;
(2)DG∶AB= .
27.(2021·阜宁模拟)如图,在直角坐称系中,半径为1的⊙A圆心A的坐标为(﹣1,0),点P为直线y=﹣ x+2上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是 .
28.(2021·岳阳模拟)如图, 内接于⊙O, 平分 交 边于点E,过点D作⊙O的切线,过点A作 于点F,设 ,⊙O的半径为R, 则下列结论正确的是 .(写出所有正确结论的序号)
① ;② ;③ ;④ .
29.(2020九上·嘉兴期中)如图,C、D是以AB为直径的圆O上的两个动点(点C、D不与A、B重合),在运动过程中弦CD始终保持不变,M是弦CD的中点,过点C作CP⊥AB于点P.若CD=3,AB=5,PM最大值是________.
30.(2020九上·麻章期中)如图,在平面直角坐标系中,⊙P的圆心是(4,a)且(a>2)半径为4,函数 的图像被⊙P截得的弦AB的长为 ,则a的值是 .
31.(2020九上·武汉月考)如图, 为 的直径,C为 上一动点,将 绕点A逆时针旋转120°得 ,若 ,则 的最大值为 .
32.(2020·潮南模拟)如图,AB是半圆O的直径,且AB=12,点C为半圆上的一点.将此半圆沿BC所在的直线折叠,若圆弧BC恰好过圆心O , 则图中阴影部分的面积是________ . (结果保留π)
33.(2020九上·长沙期末)如图, 是锐角 的外接圆, 是 的切线,切点为F, ,连结 交 于E, 的平分线 交 于D,连结 .下列结论:① 平分 ;②连接 ,点F为 的外心;③ ;④若点M,N分别是 和 上的动点,则 的最小值是 .其中一定正确的是________(把你认为正确结论的序号都填上).
34.(2020九上·龙马潭期末)如图, 内接于⊙O, ,D是⊙O上与点B关于圆心O成中心对称的点,P是 边上一点,连结 .已知 , ,Q是线段 上一动点,连结 并延长交四边形 的一边于点R,且满足 ,则 的值为________.
35.(2019·瑞安模拟)如图,已知AB为⊙O的直径,点C,E在⊙O上,且sin∠ACE= ,点D为弧BE中点,连结DE,则 的值为________.
36.(2019九上·哈尔滨月考)如图,已知AB是半圆的直径,且AB=10,弦AC=6,将半圆沿过点A的直线折叠,使点C落在直径AB上的点C′,则折痕AD的长为________.
37.(2019九下·成都开学考)如图,在矩形 中, , ,对角线 、 相交于点 ,现将一个直角三角板 的直角顶点与 重合,再绕着 点转动三角板,并过点 作 于点 ,连接 .在转动的过程中, 的最小值为________.
38.如图,AB是半圆O的直径,D是弧AB上一点,C是弧AD的中点,过点C作AB的垂线,交AB于E,与过点D的切线交于点G,连接AD,分别交CE、CB于点P、Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心.其中正确结论是________(填序号).
39.如图,在半径为5的⊙O中,弦AB=8,P是弦AB所对的优弧上的动点,连接AP,过点A作AP的垂线交射线PB于点C,当△PAB是等腰三角形时,线段BC的长为 .
40.如图,已知A,B两点的坐标分别为(2 ,0),(0,10),M是△AOB外接圆⊙C上的一点,且∠AOM=30°,则点M的坐标为 .
答案解析部分
一、单选题
1.【答案】 B
【解析】【解答】∵四边形ABCD内接于
∴∠BAD+∠DCB=180°
∵∠DCE+∠DCB=180°
∴∠BAD=∠DCE=64°
∵∠BOD、∠BAD对着圆中同一段弧
∴∠BOD=2∠BAD=2×64°=128°
故答案为:B
【分析】先求出∠BAD+∠DCB=180°,再求出∠BAD=∠DCE=64°,最后计算求解即可。
2.【答案】 C
【解析】【解答】解:连接OC,如下图:
∵ ,
∴
又∵DC切⊙O于点C,OC为半径
∴
∴ 是直角三角形
∴
∴
故答案为:C
【分析】连接OC,由于AB是直径,可知 , , 推出 是直角三角形,再利用三角形外角性质求解即可。
3.【答案】 C
【解析】【解答】要确定点与圆的位置关系,主要根据点与圆心的距离与半径的大小关系来进行判断.
当d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内.在直角△BCD中CD=AB=15,BC=20,则BD= = =25.由图可知15<r<25,
故答案为:C.
【分析】要确定点与圆的位置关系,主要根据点与圆心的距离与半径的大小关系来进行判断,当d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内.
4.【答案】 C
【解析】【解答】解:连接OD , 如图:
在 中, , , ,
由勾股定理,则
,
设半径为r , 则 ,
∴ ,
∴四边形CEOF是正方形;
由切线长定理,则 , ,
∵ ,
∴ ,
解得: ,
∴ ;
∴阴影部分的面积为: ;
故答案为:C .
【分析】连接OD , 设半径为r , 则 ,得出 ,四边形CEOF是正方形;由切线长定理,则 , ,列出方程解得出x的值即可得出答案。
5.【答案】 C
【解析】【解答】解:如图,连接 OA 过 作 垂足分别为 而
四边形 为矩形,
同理:
四边形 为正方形,
故答案为:C.
【分析】连接OA、OC,过O作OF⊥AB,OE⊥CD,垂足分别为F、E,则 四边形OEPF为矩形,由垂径定理可得AF=BF=4,结合勾股定理求出OF,同理可得OE,推出四边形OEPF为正方形,则FP=FO=3,然后由勾股定理可得OP的值.
6.【答案】 C
【解析】【解答】解:过C作CH⊥AB,延长HC交圆于P',连接AC、P'B、P'A,
当x=0时,y=-3,当y=0时,x=4,
∴A(0,-3),B(4,0),
∴AB==5,
∵BC=OB+OC=3+1=4,
∴S△ACB=BC×OA=AB×CH,
∴CH== ,
∴HP'=CH+HP'=+1= ,
∴ △PAB面积的最大值=S△P'AB=×AB×HP'=×5×= .
故答案为:C.
【分析】过C作CH⊥AB,延长HC交圆于P',连接AC、P'B、P'A, 则△PAB面积的最大值为S△P'AB ,
先求出直线AB与坐标轴交点的坐标,再利用勾股定理求出AB长,利用两点间坐标求出BC长,然后利用等积法求出CH长,则可求出HP',最后计算△P'AB的面积即可.
7.【答案】 C
【解析】【解答】解:如图,设AD中点为E,半圆圆心为O,连接OE,交半圆于P,此时PE取最小值,
∵四边形ABCD是矩形, , ,
∴AE=DE=4,OB=OC=OP=4,
∴CD=AB=OE=6,AD=BC=8,
∴PE=2,
∵点E为AD中点,
∴ =2PE2+2AE2 ,
∴ 的最小值为2PE2+2AE2=2×22+2×42=40,
故答案为:C.
【分析】设AD中点为E,半圆圆心为O,连接OE,交半圆于P,此时PE取最小值,由矩形的性质可得AE=DE,OB=OC=OP,于是由线段的构成PE=AB-OP可求得PE的值,由勾股定理可得PA2+PD2=2PE2+2AE2求解.
8.【答案】 C
【解析】【解答】延长AO交BC于点E,
∵
∴等边三角形ABE
过点O作OD BC于点D,在 中 ,
∴
设 , ,
又根据垂径定理得 ,
∵BE=AE
∴BD+DE=AO+OE
即 ,解得 ,
∴AB=BE=5+1=6.
故答案为:C.
【分析】延长AO交BC于点E,过点O作OD BC于点D,由 , 可得等边三角形ABE,设AB的长为x,由此可表示出OD、BD和DE的长;在 中 ,进而求的x的值。
9.【答案】 B
【解析】【解答】解:如图,连OI,PI,AI。
∵PH⊥OA
∴∠PHO=90°,
∴∠HOP+∠OPH=90°
又∵I为△OPH的内心
∴∠IOP=∠IOA=∠HOP,∠IPO=∠OPH
∴∠IOP+∠IPO=(∠HOP+∠OPH)=45°
∴∠PIO=180°-(∠IPO+∠IOP)=180°-45°=135°
又∵OP=OA,OI=OT,∠IOP=∠IOA
∴△OPI≌△OAI
∴∠AIO=∠PIO=135°
∴点I在以OA为弦,并且所对的圆周角为135°的一段劣弧上
过A、I、O三点作⊙O′,连O′A,O′O,在优弧AO取点P,连PA,PO。
∴∠APO=180°-∠AIO=180°-135°=45°
∴∠AO′O=90°
∴O′O=OA=×2=
∴弧OA的长=.
∴内心I所经过的路径长为。
故答案为:B.
【分析】连OI,PI,AI,先利用三角形的内心的定义求出∠PIO=135°,然后易证△OPI≌△OAI,利用相似三角形的对应角相等得到∠AIO=∠PIO=135°,所以点I在以OA为弦,并且所对的圆周角为135°的一段劣弧上;过A、I、O三点作⊙O′,连O′A,O′O,在优弧AO取点P,连PA,PO,利用圆内接四边形的性质可得∠APO=45°,进而得∠AOO=90°,则可求出O′O,然后利用弧长公式计算即可。
10.【答案】 D
【解析】【解答】解:如图,连接CE.
∵AP∥BC,
∴∠PAC=∠ACB=60°,
∴∠CEP=∠CAP=60°,
∴∠BEC=120°,
∴点E在以M为圆心,MB为半径的 上运动,
∴ 中优弧 度数为240°,劣弧 度数为120°
∴△BOC是等腰三角形,∠BOC=120°,
∵∠BCM=30°,BC= .
∴MB=MC=4,
∴连接MA交 于E′,此时AE′的值最小.
∵∠ACB=60°,∠BCO=30°,
∴∠ACM=90°,
∴MA= = ,
∴AE的最小值为=5-4=1.
故答案为:D.
【分析】如图,连接CE.首先证明∠BEC=120°,由此推出点E在以M为圆心,MB为半径的 上运动,连接MA交 于E′,此时AE′的值最小.
11.【答案】 D
【解析】【解答】解:如图,过点A作AG⊥BD于G点,
∵∠BAD=90°,
∴ ,
∵ ,
∴ ,
∴点C到BD的距离为 ,
∵BD是圆的切线,
∴圆的半径为 ,
过点P作PE⊥BD于点E,
∴∠AGT=∠PET,
∵∠ATG=∠PTE,
∴ ,
∴ ,
∴ ,
∵ ,
要使 最大,则 最大,即PE最大,
∵点P是圆上动点,BD是圆的切线,
∴PE最大为圆的直径,
即PE最大值为:3,
∴ 最大值为 ,
故答案为:D.
【分析】如图,过点A作AG⊥BD于G点,利用矩形的性质结合勾股定理求出BD,由此提高等面积法求得AG= ,从而得分析出圆的半径为 ,紧接着过点P作PE⊥BD于点E,提高证明 利用相似三角形性质得出 ,据此根据题意分析出要使 最大,则 最大,即PE最大,最后进一步分析求解即可.
12.【答案】 B
【解析】【解答】解:作AH⊥BC于H,OG⊥EF于G,连接OE、OF,如图,
∵∠EOF=2∠EAF=2×45°=90°,OE=OF,
而OE=OF,
∴EF= OE,
当OE的值最小时,EF的值最小,
此时AD最小,AD的最小值为AH的长,
在Rt△ABH中,
∵sin∠ABH==sin60°,
∴AH= ,
,∴OE的最小值为 ,
∴EF的最小值为 × = .
故答案为:B.
【分析】作AH⊥BC于H,OG⊥EF于G,连接OE、OF,如图,利用圆周角定理得∠EOF=90°,利用含30度的直角三角形三边的关系得到EF=2EG= OE,所以当⊙O的半径最小时,EF的值最小,此时AD最小,AD的最小值为AH的长,然后计算出AH的长就可得到EF的最小值.
13.【答案】 B
【解析】【解答】解:作DF⊥CA,垂足F在CA的延长线上,作DG⊥CB于点G,连接DA,DB,
∵CD平分∠ACB,
∴∠ACD=∠BCD
∴DF=DG, ,
∴DA=DB,
∵∠AFD=∠BGD=90°,
∴△AFD≌△BGD,
∴AF=BG.
易证△CDF≌△CDG,
∴CF=CG,
∵AC=6,BC=8,
∴AF=1,
∴CF=7,
∵△CDF是等腰直角三角形,
∴CD=7 ,
故答案为:B.
【分析】作DF⊥CA,交CA的延长线于点F,作DG⊥CB于点G,连接DA,DB.由CD平分∠ACB,根据角平分线的性质得出DF=DG,由HL证明△AFD≌△BGD,△CDF≌△CDG,得出CF=7,又△CDF是等腰直角三角形,从而求出CD=7 .
14.【答案】 B
【解析】【解答】根据题意可得直线经过定点D(3,4),则OD=5,当OD⊥BC时,BC取得最小值,根据垂径定理可得BC=24.
【分析】根据直线经过定点D(3,4),求出最短的弦BC是过点D且该圆直径垂直的弦,再求出OD的长,再根据以原点O为圆心过点A(13,0 ),求出OB的长,然后利用勾股定理求出BD即可.
15.【答案】 C
【解析】【解答】解:∵直线 与x轴、y轴分别交于A、B两点,
∴A点的坐标为(4,0),B点的坐标为(0,﹣3),
,即OA=4,OB=3,
由勾股定理得:AB=5,
过C作CM⊥AB于M,连接AC,
则由三角形面积公式得: ×AB×CM= ×OA×OC+ ×OA×OB,
∴5×CM=4×1+3×4,
∴CM= ,
∴圆C上点到直线 的最大距离是 = ,
∴△PAB面积的最大值是 = ,
故答案为:C.
【分析】求出A、B的坐标,根据勾股定理求出AB,求出点C到AB的距离,即可求出圆C上点到AB的最大距离,根据面积公式求出即可.
16.【答案】 A
【解析】【解答】如图,连接EB,设
∵AB是直径
∵E是 的内心,
∴点E在以D为圆心DA为半径的圆上,运动轨迹是 ,点C的运动轨迹是
∵ ,设 ,则 ,
故答案为:A
【分析】如图,连接EB,设 ,易知点E在以D为圆心DA为半径的圆上,运动轨迹是 ,点C的运动轨迹是 ,由题意 ,设 ,则 ,利用弧长公式计算后即可解决问题.
17.【答案】 B
【解析】【解答】解:设⊙O与MN相切于点K,设正方形的边长为2a.
∵AD、CD、MN是切线,
∴AE=DE=DF=CF=a,MK=ME,NK=NF,设MK=ME=x,NK=NF=y,
在Rt△DMN中,∵MN=x+y,DN=a﹣y,DM=a﹣x,
∴(x+y)2=(a﹣y)2+(a﹣x)2 ,
∴ax+ay+xy=a2 ,
∵S△BMN=S正方形ABCD﹣S△ABM﹣S△DMN﹣S△BCN=8,
∴4a2﹣ ×2a×(a+x)﹣ (a﹣x)(a﹣y)﹣ ×2a×(a+y)=8,
∴ a2﹣ (ax+ay+xy)=8,
∴a2=8,
∴a=2 ,
∴AB=2a=4 ,
∴⊙O的半径为2 ,
故答案为:B.
【分析】设⊙O与MN相切于点K,设正方形的边长为2a.因为AD、CD、MN是切线,可得AE=DE=DF=CF=a,MK=ME,NK=NF,设MK=ME=x,NK=NF=y,在Rt△DMN中,以为MN=x+y,DN=a-y,DM=a-x,看到(x+y)2=(a-y)2+(a-x)2 , 推出ax+ay+xy=a2 , 根据S△BMN=S正方形ABCD-S△ABM-S△DMN-S△BCN=8,构建方程求出a即可解决问题;
18.【答案】 D
【解析】【解答】解: 当直线y=﹣x+b与圆相切,且函数经过一、二、四象限时,如图.
在y=﹣x+b中,令x=0时,y=b,则与y轴的交点是(0,b),
当y=0时,x=b,则A的交点是(b,0),
则OA=OB,即△OAB是等腰直角三角形.
连接圆心O和切点C.则OC=2.
则OB= OC=2 .即b=2 ;
同理,当直线y=﹣x+b与圆相切,且函数经过二、三、四象限时,b=﹣2 .
则若直线y=﹣x+b与⊙O相交,则b的取值范围是﹣2 <b<2 .
故答案为:D.
【分析】求出直线y=-x+b与圆相切,且函数经过的象限分别求出此时b的值,则相交时b的值在相切时的两个b的值之间.
19.【答案】 D
【解析】【解答】解:如图,连接OQ,作CH⊥AB于H.
∵AQ=QP,
∴OQ⊥PA,
∴∠AQO=90°,
∴点Q的运动轨迹为以AO为直径的⊙K,连接CK,
当点Q在CK的延长线上时,CQ的值最大,
在Rt△OCH中,∵∠COH=60°,OC=2,
∴OH= OC=1,CH= ,
在Rt△CKH中,CK= = ,
∴CQ的最大值为1+ ,
故答案为:D.
【分析】如图,连接OQ,作CH⊥AB于H,根据垂径定理可得OQ⊥PA,即得∠AQO=90°,从而可判断点Q的运动轨迹为以AO为直径的⊙K,连接CK,可得当点Q在CK的延长线上时,CQ的值最大.在Rt△OCH中,利用直角三角形的性质可求出OH、CH的长,在Rt△CKH中利用勾股定理求出CK的长,从而求出CQ的长.
20.【答案】 A
【解析】【解答】∵AB为直径,
∴AE⊥BC,
∵AB=AC,
∴∠EAB=BAC,=∠CBF,
EB=CE=CB,
∴∠CBF=∠EAB,tan∠EAB== ,
∴∠CBF+∠ABC=∠EAB+∠ABC=90°,
∴FB是⊙O的切线,
∴FB2=FD FA,
在RT△AEB中,AB=10,
∴EB= ,
∴CB=2 , CE=,
∵CE CB=CD AC,AC=10,
∴CD=2,
∴AD=AC-CD=8,
设CF=x,则FD=x+2,FA=10+x,FB2=AF2-AB2=(10+x)2-102,
∴(10+x)2-102=(x+2)(10+x),
整理得:x= ,
∴CF= ,
答案为;A
【分析】连接AE,根据AB是直径,得出AE⊥BC,CE=EB,依据已知条件得出∠CBF=∠EAB,BF是圆的切线,进而得出BC的长,然后根据割线定理求得CD的长,最后根据切割线定理求得FC
二、填空题
21.【答案】 2
【解析】【解答】如图,连接OA、OB、OC、OD、OE、OF
∵⊙O为 的内切圆,切点分别为D、E、F
∴OD⊥AB,OE⊥AC,OF⊥BC,且OD=OE=OF
在Rt△ABC中,由勾股定理得
∴
∵
∴
即
∴OD=2
即⊙O的半径为2
故答案为:2
【分析】利用勾股求出AC,然后利用 , 得到关于半径的方程,求解即可得出答案。
22.【答案】
【解析】【解答】解:如图,连接OF.
∵DE⊥AB,
∴DE=EF, ,
∵点D是弧AC的中点
∴ ,
∴ ,
∴AC=DF=12,
∴EF= DF=6,设OA=OF=x,
在Rt△OEF中,则有x2=62+(x-3)2 ,
解得x= .
故答案为:.
【分析】连接OF,由垂径定理可得DE=EF, , 根据点D是弧AC的中点可得 , 推出 , 根据等弧所对的弦相等得AC=DF=12,由垂径定理可得EF,设OA=OF=x,然后在Rt△OEF中,应用勾股定理求解即可.
23.【答案】
【解析】【解答】解:作点B关于MN的对称点C,连接AC交MN于点P,则P点就是所求作的点.
此时PA+PB最小,且等于AC的长.
连接OA,OC,OB,作OD⊥AC于D,
∵∠AMN=40°,
∴∠AON=80°,
∵B为弧AN的中点,
∴∠AOB=∠NOB=40°,
由对称可知,∠CON=∠NOB=40°,
∴∠AOC=120°,
∵MN=2
∴OA=OC=1,
∴∠OAC=∠OCA=30°,
∴OD= ,
,
AC=2CD= .
故答案为: .
【分析】作点B关于MN的对称点C,连接AC交MN于点P,此时PA+PB最小,且等于AC的长,连接OA,OC,OB,作OD⊥AC于D,由圆周角定理可得∠AON=2∠AMN=80°,根据中点的概念可得∠AOB=∠NOB=40°,由对称可知:∠CON=∠NOB=40°,则∠AOC=120°,易得OA=OC=1,然后求出OD、CD,进而可得AC.
24.【答案】 8
【解析】【解答】解:如图,连接AD,
∵AB为直径,
∴∠ACB=∠ADB=90°,
∵CD为∠ACB的角平分线,
∴∠BCD=45°,
∴∠BAD=∠BCD=45°,
∴AB=BD= 5 ,
∴BC==8.
故答案为:8.
【分析】连接AD,由圆周角定理得出∠ACB=∠ADB=90°,然后由根据角平分线的定义求出∠BCD=45°,再由同弧所对的圆周角定理求出∠BAD=45°,则由等腰直角三角形的性质求出AB长,最后由勾股定理求BC长即可.
25.【答案】 3 +3
【解析】【解答】解:如图,作△AOC的外接圆⊙P,过点P作PQ⊥AC与Q,延长QP⊙P于O',连接PA、PC.
当点O在圆周上运动到点O',即点O与O'重合时,点O到AC距离最大.
∵∠MON=45°,
∴∠CO'A=45°,
∴∠CPA=90°,
∵PQ⊥AC,
∴QA=QC= AC=3,
∴PQ= AC=3,
PA= QA=3 ,
OP=AP=3 ,
∴O'Q=OP+PQ=3 +3.
故答案为:3 +3.
【分析】作△AOC的外接圆⊙P,过点P作PQ⊥AC与Q,延长QP⊙P于O',连接PA、PC;由题意知:当点O在圆周上运动到点O',即点O与O'重合时,点O到AC距离最大。根据O'Q=OP+PQ可求解.
26.【答案】 (1)3
(2)12:25
【解析】【解答】解:过点C作CF⊥AB于点F,
∵点C是弧DB的中点
∴弧CD=弧BC,
∴∠DAC=∠BAC,CD=BC
∴AC平分∠DAB,
∵CE⊥CD,
∴FC=CE,
在Rt△DEC和R△BFC中
∴Rt△DEC≌R△BFC(HL)
同理可证△AEC≌△ACF
∴S△DEC=S△BFC=1,S△AEC=S△ACF ,
∵S△ABC=S△ACF+S△BFC=5
∴S△AEC=S△ACF=5-1=4,
∴S△ADC=S△AEC-S△DEC=4-1=3.
故答案为:3.
(2)连接OC,BD交于点H,
∵
∴DA=3DE,
设DE=a,则DA=3a,
∵AB是圆的直径,
∴∠ADB=∠EDH=90°=∠E,
∵点C是弧BD的中点,
∴OC⊥BD
∴∠DHC=90°,
∴四边形DEHC是矩形,
∴CH=DE=a,
OH是△ADB的中位线
∴
∴OC=CH+OH=a+=
∴AB=2OC=5a,
∴ ,
∵
∴5a·DG=3a·4a
解之:DG=2.4a
∴DG∶AB=2.4a:5a=12:25.
故答案为:12:25.
【分析】 (1)过点C作CF⊥AB于点F,利用弧的中点及等弧所对圆周角相等,可知AC平分∠DAB,CD=BC,利用角平分线的性质可得到FC=CE;利用HL可证得Rt△DEC≌R△BFC,△AEC≌△ACF,利用全等三角形的面积相等可推出S△DEC=S△BFC=1,S△AEC=S△ACF , 从而可求出△AEC的面积及△ACD的面积.
(2)连接OC,BD交于点H,利用△CDE和△ADC的面积可证得DA=3DE,设DE=a,则DA=3a;利用直径所对圆周角是直角,可证得∠ADB=∠EDH=90°=∠E,利用垂径定理可证得∠DHC=90°,由此可推出四边形DEHC是矩形,可得到CH=a,利用三角形的中位线定理可求出OH的长,即可表示出圆的半径,再表示出圆的直径AB的长;再利用勾股定理求出BD的长,利用直角三角形的两个面积公式可表示出DG的长;然后求出DG∶AB的值.
27.【答案】 2
【解析】【解答】解:过点P作⊙A的切线,切点为Q,连接AP、AQ,设直线 与x、y轴的交点分别为B、C,如图所示:
∴∠AQP=90°,
令y=0时,则 ,解得 ,令x=0时,则y=2,
∴OC=2,OB=4,
∵半径为1的⊙A圆心A的坐标为(﹣1,0),
∴ ,
∴AB=5,
∴在Rt△PQA中, ,
∴当切线长PQ为最小时,则AP为最小,由此可得当AP与直线 垂直时AP取最小,连接AC,则由勾股定理可得 ,
∴ ,
∴AC⊥BC,
∴当点P与点C重合时,PQ取最小值,如图所示,
∵OA=AQ,AC=AC,∠AQP=∠AOP=90°,
∴△AQP≌△AOP(HL),
∴OP=PQ=2,
∴PQ的最小值为2;
故答案为2.
【分析】过点P作⊙A的切线,切点为Q,连接AP、AQ,设直线 与x、y轴的交点分别为B、C,可得∠AQP=90°,利用勾股定理可得 , 可知当AP最小时,PQ最小,根垂线段最短,可知当AP⊥BC时,AP最小,此时当点P与点C重合时,证明Rt△AQP≌Rt△AOP,可得OP=PQ=2,据此即得结论.
28.【答案】 ①③④
【解析】【解答】解:①连接 ,如图,
∵ 平分 ,
∴ .
∴ ,
∴ .
∵ 为⊙O的切线,
∴ .
∴MN∥BC,所以①正确;
②∵
∴∠DBC=∠CAD.
∴ .
∴只有当 或∠BED=∠BAC时,
而上述的条件不具备,所以②错误;
③过A点作直径 ,连接BG,如图,
∵ 为直径,
∴ .
∵ ,
∴ .
∴ .
∵
.
∴ .
∴ .
. 所以③正确;
④过D点作 于P, 交AC的延长线于点Q,连接DC.如图,
∵ 平分 ,
∴ , .
∴
∴ .
在 中, ,
∴ .
同理,在 中, .
在 和 中,
,
∴ .
∴ ,
即 .
∴ .
∴ .所以④正确.
故答案为:①③④.
【分析】连接OD,由角平分线的概念可得∠BAD=∠CAD,推出OD⊥BC,由切线的性质可得OD⊥MN,据此可判断①;由圆周角定理可得∠DBC=∠CAD,推出∠DBC=∠BAD,然后根据相似三角形的判定定理可判断②;过A点作直径AG,连接BG,由圆周角定理可得∠ABG=90°,由垂直的概念可得∠AFC=90°,证明△ABG∽△AFC,由相似三角形的性质可判断③;过D点作DP⊥AB于P, DQ⊥AC交AC的延长线于点Q,连接DC,易得∠BAD=∠QAD=α,DP=DQ,DB=DC,证明△DBP≌△DCQ,得到BP=CQ,即AB-AP=AQ-AC,据此判断④.
29.【答案】 2.5
【解析】【解答】解:当CD∥AB时,PM最长,连接OM,CO,
∵CD∥AB,CP⊥CD,
∴CP⊥AB
∵点M是CD的中点,OM过点O
∴OM⊥CD,
∴∠OMC=∠PCD=∠CPO=90°,
∴四边形CPOM是矩形,
∴PM=OC,
OC=AB=2.5
∴PM=2.5.
故答案为:2.5
【分析】当CD∥AB时,PM最长,连接OM,CO,利用垂径定理易证OM⊥CD,再证明∠OMC=∠PCD=∠CPO=90°,可推出四边形CPOM是矩形,利用矩形的对角线相等,可证得PM=OC,从而可求出PM的长。
30.【答案】
【解析】【解答】解:如图:过P点作PE⊥AB于E,过P点作PC⊥x轴于C,交AB于D,连接PA.
∵PE⊥AB,AB=4 ,半径为4,
∴AE= AB=2 ,PA=4,
根据勾股定理得:PE= ,
∵点A在直线y=x上,∴∠AOC=45°,
∵∠DCO=90°,∴∠ODC=45°,
∴△OCD是等腰直角三角形,∴OC=CD=4,
∴∠PDE=∠ODC=45°,∴∠DPE=∠PDE=45°,
∴DE=PE=2,∴PD=2 ∵⊙P的圆心是(4,a),
∴a=PD+DC=4+2 .
故答案为4+2
【分析】先求出AE= AB=2 ,PA=4,再求出PD=2 , 最后计算求解即可。
31.【答案】
【解析】【解答】解:将△ABD绕点A顺时针旋转120°,则D与点C重合,B′是定点,
BD的最大值即B′C的最大值,当B′,O,C三点共线时,BD最大
过点B′作B′E⊥AB,交BA的延长线于点E
由题意可得A′B=AB=4,∠EAB′=60°
∴AE=2,B′E= ,OC=OB=2
在Rt△OEB′中,B′O=
∴B′D= B′O+OC= .
故答案为: .
【分析】将△ABD绕点A顺时针旋转120°,则D与点C重合,B′是定点,BD的最大值即B′C的最大值,过点B′作B′E⊥AB,交BA的延长线于点E,由题意可得A′B=AB=4,∠EAB′=60°,求出AE、B′E、OC的值,在Rt△OEB′中,应用勾股定理求出B′O,据此求解.
32.【答案】 6π
【解析】【解答】
做出辅助线,如图所示,在Rt三角形BOD中, OB=R=6,OD=3
所以∠OBD=30°,∠AOC=60°,
∴阴影部分面积对应的圆心角为60°,代入公式可得
【分析】根据直角三角形的性质可得出角的度数的关系,利用扇形面积公式可得出阴影部分面积。
33.【答案】
【解析】【解答】解:如图 ,连接 ,
∵ 是 的切线,
∴ ,∵
∴ ,且 为半径
∴ 垂直平分
∴
∴
∴ 平分 ,故 符合题意
点 的外心,故 符合题意;
如图 ,过点C作 交 的延长线与点G
,故 符合题意;
如图 ,作点M关于 的对称点 ,
点M与点 关于 对称,
当点N在线段 上,且 时, ,
且
∴ 的最小值为 ;故 符合题意.
故答案为: .
【分析】如图1,连接 ,通过切线的性质证 ,进而由 ,即可由垂径定理得到F是 的中点,根据圆周角定理可得 ,可得 平分 ;由三角形的外角性质和同弧所对的圆周角相等可得 ,可得 ,可得点F为 得外心;如图 2 ,过点C作 交 的延长线与点G通过证明 ,可得 ;如图 3 ,作点M关于 的对称点 ,当点N在线段 上,且 时, .
34.【答案】 1或
【解析】【解答】解:因为 内接于圆, ,D是⊙O上与点B关于圆心O成中心对称的点,
∴AB=BC=CD=AD,
是正方形
①点R在线段AD上,
∵AD∥BC,
∴∠ARB=∠PBR,∠RAQ=∠APB,
∵AP=BR,
∴△BAP≌ABR,
∴AR=BP,
在△AQR与△PQB中,
,
②点R在线段CD上,此时△ABP≌△BCR,
∴∠BAP=∠CBR.
∵∠CBR+∠ABR=90°,
∴∠BAP+∠ABR=90°,
∴BQ是直角△ABP斜边上的高,
∴QR=BR-BQ=5-2.4=2.6,
.
故答案为:1或 .
【分析】首先证明四边形ABCD为正方形,即可得到AD∥BC,根据题意,由R点的位置,判断得到答案即可。
35.【答案】
【解析】【解答】解:连接OD,BD,AD,AE,BE,
∴∠ACE=∠ABE,
∵sin∠ACE= ,
∴sin∠ABE= = ,
∴设AE= x,AB=5x,
∴BE= =2 x,
∵点D为弧BE中点,
∴OD⊥BE,OD平分BE,
设OD,BE相交于H,
∴BH=EH= x,
∴OH= = x2 ,
∴DH= x2 ,
∵∠BAD=∠DBH,∠ADB=∠BHD=90°,
∴△BDH∽△ABD,
∴ ,
∴ = = ,
∴BD2= x,
∴AD2= x,
∵点D为弧BE中点,
∴BD=DE,
∴ = = ,
故答案为: .
【分析】连接OD,BD,AD,AE,BE,得到∠ACE=∠ABE,求得sin∠ABE= =
, 设AE= x,AB=5x,根据勾股定理得到BE= =2 x,根据垂径定理得到OD⊥BE,OD平分BE,设OD,BE相交于H,得到BH=EH= x,根据勾股定理得到OH= = x,求得DH= x,根据相似三角形的性质即可得到结论.
36.【答案】 .
【解析】【解答】
设圆的圆心是O,连接OD,作DE⊥AB于E,OF⊥AC于F.
根据题意知,∵OF⊥AC,∴AF= AC=3,
∵∠CAD=∠BAD,∴ ,∴点D是弧BC的中点.∴∠DOB=∠OAC=2∠BAD,
在△AOF和△OED中,∵∠OFA=∠OED,∠FAO=∠EDO,AO=DO,
∴△AOF≌△OED(AAS),∴OE=AF=3,
∵DO=5,∴DE=4,∴AD= .
故答案为 .
【分析】通过作辅助线,结合三角形全等的性质与判定,利用勾股定理求出线段的长度即可.
37.【答案】
【解析】【解答】解:∵∠OHD=90°,∴点H的运动轨迹为以OD为直径的圆上,
∵AB=4,BC=4 , ∴AC=BD=8, ∴AO=OD=4,
设OD的中点为M,则圆M的半径为2,∴AM= ,
当A、H、M三点在同一条直线上时,AH最短,则AH= .
【分析】首先根据∠OHD=90°得出点H的运动轨迹,根据直角三角形的勾股定理得出AO和OD的长度,设OD的中点为M,根据Rt△AOM的勾股定理得出AM的长度,从而得出最小值.
38.【答案】 ②③
【解析】【解答】∵在 中,AB是直径,点D是 上一点,点C是 的中点,
故①错误;
连接OD,
则OD⊥GD,∠OAD=∠ODA,
∴∠GPD=∠GDP;
∴GP=GD,故②正确;
∵弦CE⊥AB于点F,
∴A为 的中点,即
又∵C为 的中点,
∴∠CAP=∠ACP,
∴AP=CP.
∵AB为 的直径,
∴∠PCQ=∠PQC,
∴PC=PQ,
∴AP=PQ,即P为Rt△ACQ斜边AQ的中点,
∴P为Rt△ACQ的外心,故③正确;
故答案为:②③.
【分析】①由等弧所对圆周角相等可得两角相等,但弧BD与弧CD不一定相等,故①错误;②连接OD,结合切线的定义及GE⊥AB即可利用等角的余角相等证得∠GPD=∠GDP,再利用等角对等边即可得证 GP=GD ;③证P为Rt△ACQ的外心即证点P到三角形三个顶点的距离相等,又因为∠ACB是直径AB所对的圆周角,故∠ACB=90° ,即三角形ACQ为直角三角形,故只需证点P为其斜边AQ的中点即可.
39.【答案】 8, ,
【解析】【解答】解:①当BA=BP时,
易得AB=BP=BC=8,即线段BC的长为8.
②当AB=AP时,如图1,延长AO交PB于点D,过点O作OE⊥AB于点E,则AD⊥PB,AE=AB=4,
∴BD=DP,
在Rt△AEO中,AE=4,AO=5,
∴OE=3,
易得△AOE∽△ABD,
∴= ,
∴BD= ,
∴BD=PD= , 即PB= ,
∵AB=AP=8,
∴∠ABD=∠P,
∵∠PAC=∠ADB=90°,
∴△ABD∽△CPA,
∴= ,
∴CP= ,
∴BC=CP﹣BP=-=;
③当PA=PB时
如图2,连接PO并延长,交AB于点F,过点C作CG⊥AB,交AB的延长线于点G,连接OB,
则PF⊥AB,
∴AF=FB=4,
在Rt△OFB中,OB=5,FB=4,
∴OF=3,
∴FP=8,
易得△PFB∽△CGB,
∴== ,
设BG=t,则CG=2t,
易得∠PAF=∠ACG,
∵∠AFP=∠AGC=90°,
∴△APF∽△CAG,
∴= ,
∴= , 解得t= ,
在Rt△BCG中,BC=t= ,
综上所述,当△PAB是等腰三角形时,线段BC的长为8, , ,
故答案为:8, , .
【分析】①当BA=BP时,利用直角三角形斜边的中线等于斜边的一半;
②当AB=AP时,如图1,延长AO交PB于点D,过点O作OE⊥AB于点E,易得△AOE∽△ABD,利用相似三角形的性质求得BD,PB,然后利用相似三角形的判定定理△ABD∽△CPA,代入数据得出结果;
③当PA=PB时,如图2,连接PO并延长,交AB于点F,过点C作CG⊥AB,交AB的延长线于点G,连接OB,则PF⊥AB,易得AF=FB=4,利用勾股定理得OF=3,FP=8,易得△PFB∽△CGB,利用相似三角形的性质=, 设BG=t,则CG=2t,利用相似三角形的判定定理得△APF∽△CAG,利用相似三角形的性质得比例关系解得t,在Rt△BCG中,得BC.
40.【答案】 (4 ,4).
【解析】【解答】∵A,B两点的坐标分别为(2 ,0),(0,10),
∴OB=10,OA=2 ,
∴AB= =4 ,
∵∠AOB=90°,
∴AB是直径,CM=2 ,
∴Rt△AOB外接圆的圆心为AB中点,
∴C点坐标为( ,5),
过点C作CF∥OA,过点M作ME⊥OA于E交CF于F,作CN⊥OE于N,如图所示:
则ON=AN= OA= ,
设ME=x,
∵∠AOM=30°,
∴OE= x
∴∠CFM=90°,
∴MF=5﹣x,CF= x﹣ ,CM=2 ,
在△CMF中,根据勾股定理得:( x﹣ )2+(5﹣x)2=(2 )2 ,
解得:x=4或x=0(舍去),
∴OE= x=4
故答案为:(4 ,4).
【分析】过点C作CF∥OA,过点M作ME⊥OA于E交CF于F,作CN⊥OE于N;由圆周角性质易得直径AB=2;A,B两点的坐标分别为(2 ,0),(0,10)结合AB的中点O利用中位线易得C点坐标为( ,5),设ME=x,则利用前面所给条件可得MF=5﹣x,CF= x﹣ ,CM=2 ;在Rt△CFM中利用勾股定理可列方程( x﹣ )2+(5﹣x)2=(2 )2 , 解得ME=4,从而得到点M的坐标(4 ,4)。
