四川省成都市蓉城名校联盟2021-2022学年高一上学期期末联考数学试题(Word版含答案)
文档属性
| 名称 | 四川省成都市蓉城名校联盟2021-2022学年高一上学期期末联考数学试题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 516.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-03 15:41:24 | ||
图片预览



文档简介
蓉城名校联盟2021~202学年度上期高中2021级期末联考
数学
考试时间120分钟,满分150分
注意事项:
1.答题前,考生务必在答题卡上将自己的学校、姓名、班级、准考证号用0.5毫米黑色签字笔填写清楚,考生考试条形码由监考老师粘贴在答题卡上的“条形码粘贴处”。
2.选择题使用2B铅笔填涂在答题卡上对应题目标号的位置上,如需改动,用橡皮擦擦干净后再填涂其它答案;非选择题用0.5毫米黑色签字笔在答题卡的对应区域内作答,超出答题区域答题的答案无效;在草稿纸上、试卷上答题无效。
3.考试结束后由监考老师将答题卡收回。
一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合,,则( )
A. B. C. D.
2.下列函数表示同一函数的是( )
A.与 B.与
C.与 D.与
3.已知角的顶点为坐标原点,始边为x轴的非负半轴,若是角终边上的一点,且,则y的值为( )
A. B. C. D.
4.设函数则的值为( )
A.1 B.2 C.3 D.4
5.已知某扇形的圆心角为,面积为,则该扇形的弧长为( )
A. B. C. D.
6.函数的零点所在的区间可以是( )
A. B. C. D.
7.已知函数,则函数的单调递减区间是( )
A. B.
C. D.
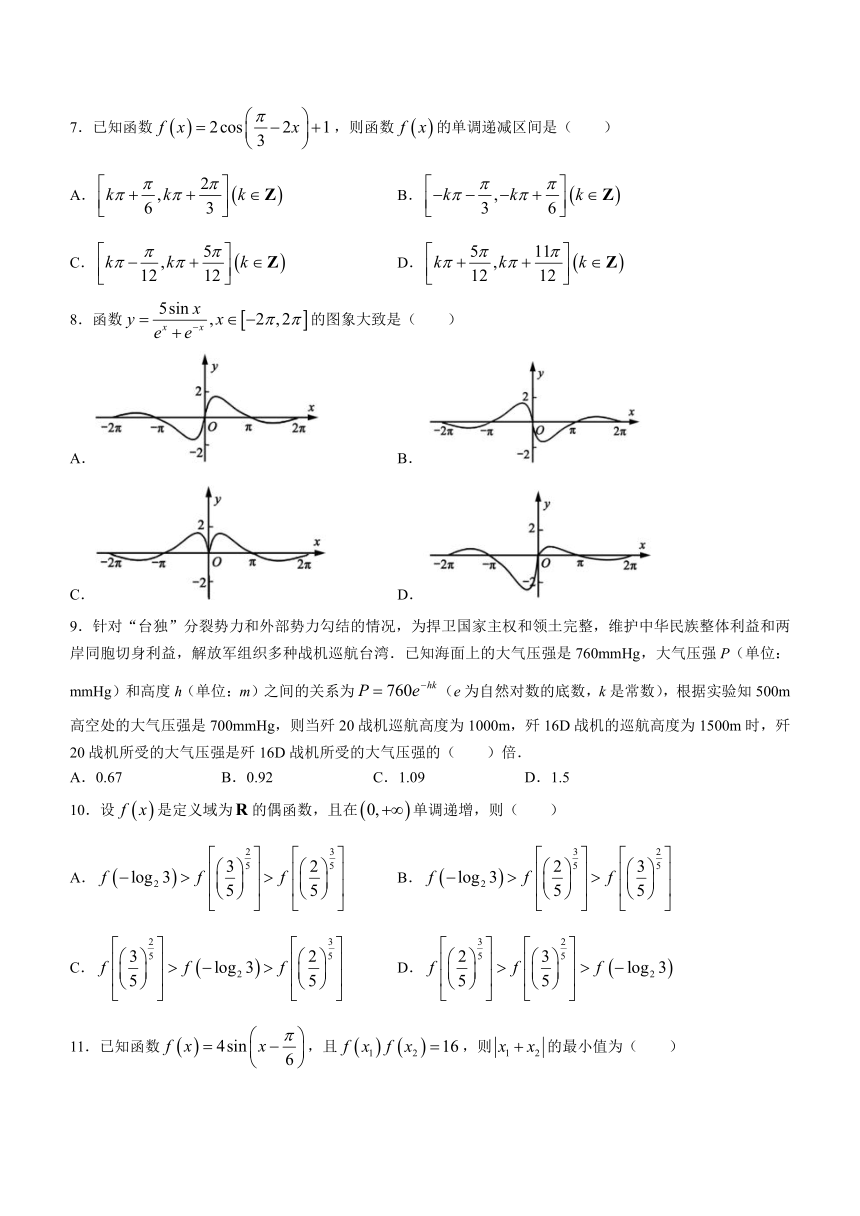
8.函数的图象大致是( )
A. B.
C. D.
9.针对“台独”分裂势力和外部势力勾结的情况,为捍卫国家主权和领土完整,维护中华民族整体利益和两岸同胞切身利益,解放军组织多种战机巡航台湾.已知海面上的大气压强是760mmHg,大气压强P(单位:mmHg)和高度h(单位:m)之间的关系为(e为自然对数的底数,k是常数),根据实验知500m高空处的大气压强是700mmHg,则当歼20战机巡航高度为1000m,歼16D战机的巡航高度为1500m时,歼20战机所受的大气压强是歼16D战机所受的大气压强的( )倍.
A.0.67 B.0.92 C.1.09 D.1.5
10.设是定义域为的偶函数,且在单调递增,则( )
A. B.
C. D.
11.已知函数,且,则的最小值为( )
A. B. C. D.
12.若,则( )
A. B. C. D.
二、填空题:本题共4小题,每小题5分,共20分。
13.已知,则______。
14.已知幂函数的图象过点,则______。
15.定义在上的函数满足:对于任意的,,都有恒成立,且对于任意,都有,同时,则不等式的解集为______。
16.已知函数,,,,对任意,总存在,使得成立,则实数m的取值范围为______。
三、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(10分)
计算求值:
(1).
(2).
18.(12分)
已知,其中且.
(1)判断的奇偶性并证明;
(2)解不等式:.
19.(12分)
集合,,.
(1)求;
(2)请从①,②,③这三个条件中任选一个作为已知条件,求实数a的取值范围.
20.(12分)
已知.
(1)化简;
(2)若,且,求的值;
(3)若,求的值.
21.(12分)
已知二次函数同时满足以下条件:①,②,③.
(1)求函数的解析式;
(2)若,,求:
①的最小值;
②讨论关于m的方程的解的个数.
22.(12分)
已知函数,,与互为反函数.
(1)求的解析式;
(2)若函数在区间内有最小值,求实数m的取值范围;
(3)若函数,关于方程有三个不同的实数解,求实数a的取值范围.
蓉城名校联盟2021~2022学年度上期高中2021级期末联考
数学参考答案及评分标准
一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1~5CDBAB 6~10AAACA 11~12BB
二、填空题:本题共4小题,每小题5分,共20分。
13. 14.1 15. 16.
三、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(10分)
解:(1)原式.
(2)原式.
18.(12分)
解:(1)为奇函数.
证明如下:
要使函数有意义,则有,
∴的定义域为,(注:不求定义域扣2分)
∵,∴为奇函数.
(2),即,当时,,即,
当时,,即,
综上:
当时,解集为;当时,解集为.
19.(12分)
解:(1),解得:,∴
,解得:,∴,
∴.
(2)选①:∵,∴
当,即时,满足题意;
当,即时,;满足,
∴综上:.
选②:当,即时,满足题意;
当,即时,或,解得或.
所以:或,
综上:.
选③:由题知:,当,即时,满足题意;
当,即时,;满足,
∴综上:.
20.(12分)
解:(1).
(2)由可知:
,
又∵,∴,则.
(3)∵,
∴.
21.(12分)
解:(1)由得,对称轴为,
设,
∴,得,
∴.
(2)①,,对称轴,
ⅰ当即时,在单调递增,
,
ⅱ即时,在单调递减,在单调递增,
∴,
ⅲ当即时,在单调递减,
,
综上:
②当时,方程无解;当时,方程有4个解;当或时,方程有2个解;
当时,有3个解.(注:每写出一种情况即得1分)
22.(12分)
解:(1).(注:未写定义域不扣分)
(2)函数在区间内有最小值,
∴在内先减后增,且,
∴∴.
(3)∵,∴,∴
∴的图象如下:
因为有三个不同的实数解,设,
即有两个根,且一个在上,一个根为0,
或有两个根,且一个在上,一个在上,
①有两个根,且一个在上,一个根为0,
∴一个根为0,解得,此时,,舍去;
②有两个根,且一个在上,一个在上,
令,ⅰ当一个根在上,一个在上,
则∴∴.
ⅱ当一个根在上,一个根为2,则,解得.
此时的两根为,,满足题意.综上:a的取值范围为.
解析:
9.C
解析:设,,则,又,故答案为C.
12.B
解析:,设,则原式等价于,而显然是单调递增的函数,则.
16.
解析:当,,当,,对任意,总存在,使得成立,则,∴∴或.
数学
考试时间120分钟,满分150分
注意事项:
1.答题前,考生务必在答题卡上将自己的学校、姓名、班级、准考证号用0.5毫米黑色签字笔填写清楚,考生考试条形码由监考老师粘贴在答题卡上的“条形码粘贴处”。
2.选择题使用2B铅笔填涂在答题卡上对应题目标号的位置上,如需改动,用橡皮擦擦干净后再填涂其它答案;非选择题用0.5毫米黑色签字笔在答题卡的对应区域内作答,超出答题区域答题的答案无效;在草稿纸上、试卷上答题无效。
3.考试结束后由监考老师将答题卡收回。
一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合,,则( )
A. B. C. D.
2.下列函数表示同一函数的是( )
A.与 B.与
C.与 D.与
3.已知角的顶点为坐标原点,始边为x轴的非负半轴,若是角终边上的一点,且,则y的值为( )
A. B. C. D.
4.设函数则的值为( )
A.1 B.2 C.3 D.4
5.已知某扇形的圆心角为,面积为,则该扇形的弧长为( )
A. B. C. D.
6.函数的零点所在的区间可以是( )
A. B. C. D.
7.已知函数,则函数的单调递减区间是( )
A. B.
C. D.
8.函数的图象大致是( )
A. B.
C. D.
9.针对“台独”分裂势力和外部势力勾结的情况,为捍卫国家主权和领土完整,维护中华民族整体利益和两岸同胞切身利益,解放军组织多种战机巡航台湾.已知海面上的大气压强是760mmHg,大气压强P(单位:mmHg)和高度h(单位:m)之间的关系为(e为自然对数的底数,k是常数),根据实验知500m高空处的大气压强是700mmHg,则当歼20战机巡航高度为1000m,歼16D战机的巡航高度为1500m时,歼20战机所受的大气压强是歼16D战机所受的大气压强的( )倍.
A.0.67 B.0.92 C.1.09 D.1.5
10.设是定义域为的偶函数,且在单调递增,则( )
A. B.
C. D.
11.已知函数,且,则的最小值为( )
A. B. C. D.
12.若,则( )
A. B. C. D.
二、填空题:本题共4小题,每小题5分,共20分。
13.已知,则______。
14.已知幂函数的图象过点,则______。
15.定义在上的函数满足:对于任意的,,都有恒成立,且对于任意,都有,同时,则不等式的解集为______。
16.已知函数,,,,对任意,总存在,使得成立,则实数m的取值范围为______。
三、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(10分)
计算求值:
(1).
(2).
18.(12分)
已知,其中且.
(1)判断的奇偶性并证明;
(2)解不等式:.
19.(12分)
集合,,.
(1)求;
(2)请从①,②,③这三个条件中任选一个作为已知条件,求实数a的取值范围.
20.(12分)
已知.
(1)化简;
(2)若,且,求的值;
(3)若,求的值.
21.(12分)
已知二次函数同时满足以下条件:①,②,③.
(1)求函数的解析式;
(2)若,,求:
①的最小值;
②讨论关于m的方程的解的个数.
22.(12分)
已知函数,,与互为反函数.
(1)求的解析式;
(2)若函数在区间内有最小值,求实数m的取值范围;
(3)若函数,关于方程有三个不同的实数解,求实数a的取值范围.
蓉城名校联盟2021~2022学年度上期高中2021级期末联考
数学参考答案及评分标准
一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1~5CDBAB 6~10AAACA 11~12BB
二、填空题:本题共4小题,每小题5分,共20分。
13. 14.1 15. 16.
三、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(10分)
解:(1)原式.
(2)原式.
18.(12分)
解:(1)为奇函数.
证明如下:
要使函数有意义,则有,
∴的定义域为,(注:不求定义域扣2分)
∵,∴为奇函数.
(2),即,当时,,即,
当时,,即,
综上:
当时,解集为;当时,解集为.
19.(12分)
解:(1),解得:,∴
,解得:,∴,
∴.
(2)选①:∵,∴
当,即时,满足题意;
当,即时,;满足,
∴综上:.
选②:当,即时,满足题意;
当,即时,或,解得或.
所以:或,
综上:.
选③:由题知:,当,即时,满足题意;
当,即时,;满足,
∴综上:.
20.(12分)
解:(1).
(2)由可知:
,
又∵,∴,则.
(3)∵,
∴.
21.(12分)
解:(1)由得,对称轴为,
设,
∴,得,
∴.
(2)①,,对称轴,
ⅰ当即时,在单调递增,
,
ⅱ即时,在单调递减,在单调递增,
∴,
ⅲ当即时,在单调递减,
,
综上:
②当时,方程无解;当时,方程有4个解;当或时,方程有2个解;
当时,有3个解.(注:每写出一种情况即得1分)
22.(12分)
解:(1).(注:未写定义域不扣分)
(2)函数在区间内有最小值,
∴在内先减后增,且,
∴∴.
(3)∵,∴,∴
∴的图象如下:
因为有三个不同的实数解,设,
即有两个根,且一个在上,一个根为0,
或有两个根,且一个在上,一个在上,
①有两个根,且一个在上,一个根为0,
∴一个根为0,解得,此时,,舍去;
②有两个根,且一个在上,一个在上,
令,ⅰ当一个根在上,一个在上,
则∴∴.
ⅱ当一个根在上,一个根为2,则,解得.
此时的两根为,,满足题意.综上:a的取值范围为.
解析:
9.C
解析:设,,则,又,故答案为C.
12.B
解析:,设,则原式等价于,而显然是单调递增的函数,则.
16.
解析:当,,当,,对任意,总存在,使得成立,则,∴∴或.
同课章节目录
