北师大版八下数学第六章 综合实践--平面图形的镶嵌课件(19张ppt)
文档属性
| 名称 | 北师大版八下数学第六章 综合实践--平面图形的镶嵌课件(19张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-04 20:28:27 | ||
图片预览




文档简介
(共19张PPT)
平面图形的镶嵌
北师大版八年级下册
第六章《综合与实践》活动
美丽的镶嵌图案
欣 赏
美丽的镶嵌图案
欣 赏
欣赏 美丽的镶嵌图案
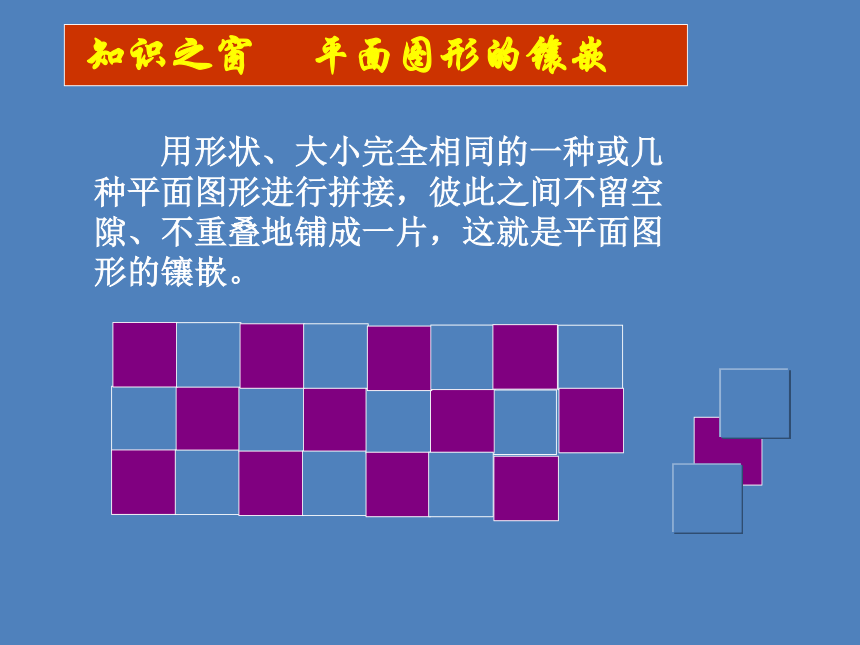
用形状、大小完全相同的一种或几
种平面图形进行拼接,彼此之间不留空
隙、不重叠地铺成一片,这就是平面图
形的镶嵌。
知识之窗 平面图形的镶嵌
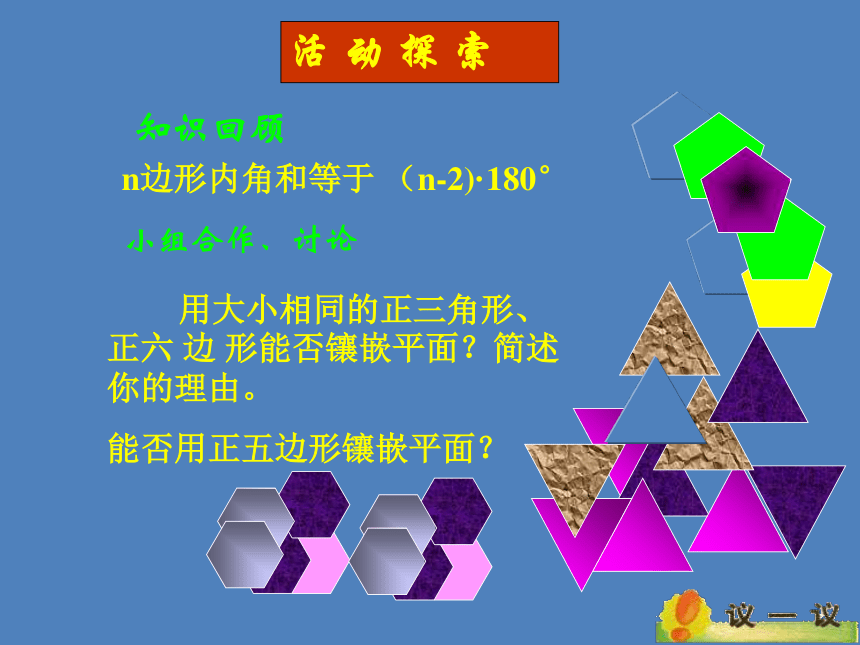
活 动 探 索
n边形内角和等于 (n-2)·180°
用大小相同的正三角形、正六 边 形能否镶嵌平面?简述你的理由。
能否用正五边形镶嵌平面?
小组合作、讨论
知识回顾
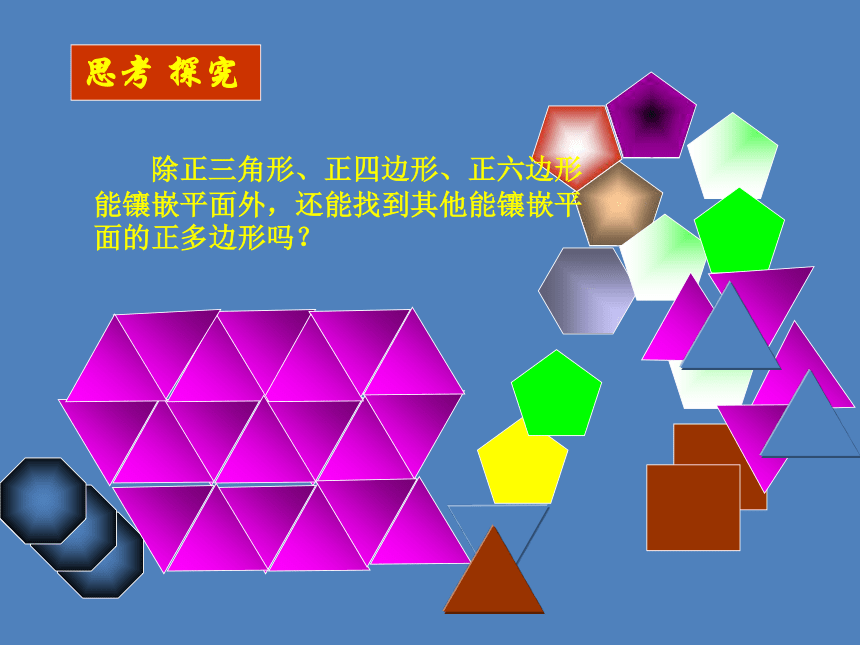
思考 探究
除正三角形、正四边形、正六边形能镶嵌平面外,还能找到其他能镶嵌平面的正多边形吗?
正方形的镶嵌
实践之窗
活 动 探 索
正五边形能否镶嵌平面
正八边形呢?
小组合作、讨论
1、用形状、大小完全相同的三角形能否
镶嵌平面?如果能,观察每个拼接点处有几个
角,它们与这种三角形的三个内角有什么关系。
如果不能,说明为什么。
2、用同一种四边形能否镶嵌平面呢?
? ?
?
?
实践活动
同桌合作拼拼摆摆
?
实践之窗
任意三角形的镶嵌
?
?
实践之窗 任意四边形的镶嵌
?
交流归纳
2.用大小相同的正 三角形、正四边形、正六边形都 可以镶嵌平面,其他正多边形都不可以镶嵌平面。
1.同一种正多边形
是否可以镶嵌平面
的关键是:一种正
多边形的一个内角
的倍数是否360°。
在每个拼结点处,设可以将m个内角彼
此无重叠、无缝隙地拼结在一起,则
× m =360° ,
整理得: (m-2)(n-2)=4,
m ,n是正整数 ,因此m-2, n-2都是4的因数, m,n的取值有三种可能:
m=6时,n=3;
m=4时,n=4 ;
m=3时,n=6。
所以正多边形边数为3、4、6时可以镶嵌平面
(n--2)×180°
n
实践心得
用同一种三角形可以镶嵌平面
用同一种四边形可以镶嵌平面
1
2
3
平面图形能镶嵌平面的条件是,每个拼接点处
的多边形各内角之和能组合成 180°或360°
美丽的镶嵌图案
收获与评价
本节课你有什么收获和感受?
本节课你有什么疑惑和问题?
你能给自己设计房子的墙壁和地面吗?
课堂小结
镶嵌的含义
镶嵌的条件
镶嵌的应用
思想方法
观察、实验、探究、合作、比较、归纳
解决问题
}
{
探索平面图形的镶嵌
实践活动
同时用边长相同的正八边形和正
方形, 能否镶嵌平面?用硬纸板为材料
进行实验验证。
你能设计一个用边长相同的其它两
种正多边形进行镶嵌的方案吗 ?
(各小组写出实践总结报告)
小组合作
数学,就在身边
平面图形的镶嵌
北师大版八年级下册
第六章《综合与实践》活动
美丽的镶嵌图案
欣 赏
美丽的镶嵌图案
欣 赏
欣赏 美丽的镶嵌图案
用形状、大小完全相同的一种或几
种平面图形进行拼接,彼此之间不留空
隙、不重叠地铺成一片,这就是平面图
形的镶嵌。
知识之窗 平面图形的镶嵌
活 动 探 索
n边形内角和等于 (n-2)·180°
用大小相同的正三角形、正六 边 形能否镶嵌平面?简述你的理由。
能否用正五边形镶嵌平面?
小组合作、讨论
知识回顾
思考 探究
除正三角形、正四边形、正六边形能镶嵌平面外,还能找到其他能镶嵌平面的正多边形吗?
正方形的镶嵌
实践之窗
活 动 探 索
正五边形能否镶嵌平面
正八边形呢?
小组合作、讨论
1、用形状、大小完全相同的三角形能否
镶嵌平面?如果能,观察每个拼接点处有几个
角,它们与这种三角形的三个内角有什么关系。
如果不能,说明为什么。
2、用同一种四边形能否镶嵌平面呢?
? ?
?
?
实践活动
同桌合作拼拼摆摆
?
实践之窗
任意三角形的镶嵌
?
?
实践之窗 任意四边形的镶嵌
?
交流归纳
2.用大小相同的正 三角形、正四边形、正六边形都 可以镶嵌平面,其他正多边形都不可以镶嵌平面。
1.同一种正多边形
是否可以镶嵌平面
的关键是:一种正
多边形的一个内角
的倍数是否360°。
在每个拼结点处,设可以将m个内角彼
此无重叠、无缝隙地拼结在一起,则
× m =360° ,
整理得: (m-2)(n-2)=4,
m ,n是正整数 ,因此m-2, n-2都是4的因数, m,n的取值有三种可能:
m=6时,n=3;
m=4时,n=4 ;
m=3时,n=6。
所以正多边形边数为3、4、6时可以镶嵌平面
(n--2)×180°
n
实践心得
用同一种三角形可以镶嵌平面
用同一种四边形可以镶嵌平面
1
2
3
平面图形能镶嵌平面的条件是,每个拼接点处
的多边形各内角之和能组合成 180°或360°
美丽的镶嵌图案
收获与评价
本节课你有什么收获和感受?
本节课你有什么疑惑和问题?
你能给自己设计房子的墙壁和地面吗?
课堂小结
镶嵌的含义
镶嵌的条件
镶嵌的应用
思想方法
观察、实验、探究、合作、比较、归纳
解决问题
}
{
探索平面图形的镶嵌
实践活动
同时用边长相同的正八边形和正
方形, 能否镶嵌平面?用硬纸板为材料
进行实验验证。
你能设计一个用边长相同的其它两
种正多边形进行镶嵌的方案吗 ?
(各小组写出实践总结报告)
小组合作
数学,就在身边
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
