指数函数
图片预览










文档简介
课件39张PPT。3.1. 2 指数函数
?第1课时 指数函数
学习目标
学习导航重点难点
重点:指数函数的概念.
难点:性质的应用.函数____________________________叫做指数函数,其中x是自变量,a 为常数.1.指数函数的定义y=ax(a>0且a≠1,x∈R)想一想
1.y=2.5x是指数函数吗?
提示:是.做一做
1.指出下列函数中,哪些是指数函数.
(1)y=(-4)x;
(2)y=x4;
(3)y=(a2+2)-x;
(4)y=2·3x+a(a≠0);
(5)y=4x2.(4)y=2·3x+a(a≠0),3x前面系数为2≠1,故它不是指数函数;
(5)y=4x2,底数是自变量,且前面系数为4,故它不是指数函数.
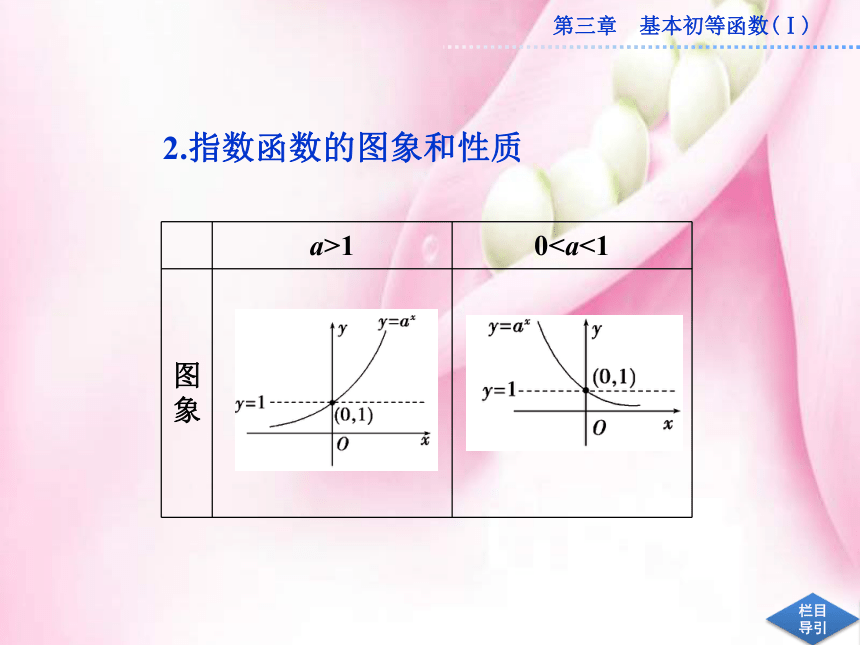
故(3)为指数函数.2.指数函数的图象和性质(0,1)01增函数减函数想一想
提示:关于y轴对称.
做一做
2.函数y=ax-1+2012(a>0且a≠1)中,无论a取何值恒经过一个定点,则这个定点的坐标为________.
答案:(1,2013) 函数y=(a2-3a+3)ax是指数函数,求a的值.【名师点评】 判断一个函数是否为指数函数只需判定其解析式是否符合y=ax(a>0,且a≠1)这一形式,否则就不是指数函数.变式训练
1.下列函数中,哪些是指数函数?
(1)y=10x;
(2)y=10x+1;
(3)y=-4x;
(4)y=xx;
(5)y=xα(α是常数).解:(1)y=10x符合定义,是指数函数;
(2)y=10x+1中指数是x+1而非x,不是指数函数;
(3)y=-4x中系数为-1而非1,不是指数函
数;
(4)y=xx中底数和指数均是自变量x,不符合指数函数定义,不是指数函数.
(5)y=xα中底数是自变量,不是指数函数. 【名师点评】 求定义域要根据函数自身的要求,找出关于x的不等式,解不等式或不等式组可得定义域.求值域要根据函数的定义域及单调性.变式训练
名师微博
1是常用的中间量,通过中间量比较大小是数学中常用的方法.【名师点评】 比较指数式的大小应根据所给指数式的形式,运用单调性法或中间量法来求解.变式训练
3.比较大小:
(1)1.72.5,1.73; (2)0.8-0.1,1.250.2;
(3)1.70.3,0.93.1; (4)0.30.2,0.20.3.
解:(1)∵函数y=1.7x在R上是增函数,
又∵2.5<3,∴1.72.5<1.73.
2.若集合 M={y|y=2x,x∈R},N={y|y=x2, x∈R},则集合 M,N 的关系为( )
A.M? N B.M?N
C.N? M D.M=N
解析:选A.x∈R,y=2x>0,y=x2≥0,即
M={y|y>0},N={y|y≥0},所以M N.方法技巧
1.指数函数的结构特征
判断一个函数是否是指数函数,关键是看解析是否符合y=ax(a>0,a≠1,x∈R)这一结构形式.指数函数具有以下特征:(1)底数a为大于0且不等于1的常数,不含有自变量x;
(2)指数位置是自变量x,且x的系数是1;
(3)ax的系数是1.2.比较幂的大小的常用方法
(1)对于底数相同,指数不同的两个幂的大小比较,可以利用指数函数的单调性来判断;
(2)对于底数不同,指数相同的两个幂的大小比较,可以利用指数函数图象的变化规律来判断;(3)对于底数不同,且指数也不同的幂的大小比较,则应通过中间值来比较;
(4)对于三个(或三个以上)的数的大小比较,则应先根据值的大小(特别是与 0、1 大小)进行分组,再比较各组数的大小即可.
失误防范
求函数的值域时一定要考虑定义域,否则易出错.本部分内容讲解结束按ESC键退出全屏播放
?第1课时 指数函数
学习目标
学习导航重点难点
重点:指数函数的概念.
难点:性质的应用.函数____________________________叫做指数函数,其中x是自变量,a 为常数.1.指数函数的定义y=ax(a>0且a≠1,x∈R)想一想
1.y=2.5x是指数函数吗?
提示:是.做一做
1.指出下列函数中,哪些是指数函数.
(1)y=(-4)x;
(2)y=x4;
(3)y=(a2+2)-x;
(4)y=2·3x+a(a≠0);
(5)y=4x2.(4)y=2·3x+a(a≠0),3x前面系数为2≠1,故它不是指数函数;
(5)y=4x2,底数是自变量,且前面系数为4,故它不是指数函数.
故(3)为指数函数.2.指数函数的图象和性质(0,1)01增函数减函数想一想
提示:关于y轴对称.
做一做
2.函数y=ax-1+2012(a>0且a≠1)中,无论a取何值恒经过一个定点,则这个定点的坐标为________.
答案:(1,2013) 函数y=(a2-3a+3)ax是指数函数,求a的值.【名师点评】 判断一个函数是否为指数函数只需判定其解析式是否符合y=ax(a>0,且a≠1)这一形式,否则就不是指数函数.变式训练
1.下列函数中,哪些是指数函数?
(1)y=10x;
(2)y=10x+1;
(3)y=-4x;
(4)y=xx;
(5)y=xα(α是常数).解:(1)y=10x符合定义,是指数函数;
(2)y=10x+1中指数是x+1而非x,不是指数函数;
(3)y=-4x中系数为-1而非1,不是指数函
数;
(4)y=xx中底数和指数均是自变量x,不符合指数函数定义,不是指数函数.
(5)y=xα中底数是自变量,不是指数函数. 【名师点评】 求定义域要根据函数自身的要求,找出关于x的不等式,解不等式或不等式组可得定义域.求值域要根据函数的定义域及单调性.变式训练
名师微博
1是常用的中间量,通过中间量比较大小是数学中常用的方法.【名师点评】 比较指数式的大小应根据所给指数式的形式,运用单调性法或中间量法来求解.变式训练
3.比较大小:
(1)1.72.5,1.73; (2)0.8-0.1,1.250.2;
(3)1.70.3,0.93.1; (4)0.30.2,0.20.3.
解:(1)∵函数y=1.7x在R上是增函数,
又∵2.5<3,∴1.72.5<1.73.
2.若集合 M={y|y=2x,x∈R},N={y|y=x2, x∈R},则集合 M,N 的关系为( )
A.M? N B.M?N
C.N? M D.M=N
解析:选A.x∈R,y=2x>0,y=x2≥0,即
M={y|y>0},N={y|y≥0},所以M N.方法技巧
1.指数函数的结构特征
判断一个函数是否是指数函数,关键是看解析是否符合y=ax(a>0,a≠1,x∈R)这一结构形式.指数函数具有以下特征:(1)底数a为大于0且不等于1的常数,不含有自变量x;
(2)指数位置是自变量x,且x的系数是1;
(3)ax的系数是1.2.比较幂的大小的常用方法
(1)对于底数相同,指数不同的两个幂的大小比较,可以利用指数函数的单调性来判断;
(2)对于底数不同,指数相同的两个幂的大小比较,可以利用指数函数图象的变化规律来判断;(3)对于底数不同,且指数也不同的幂的大小比较,则应通过中间值来比较;
(4)对于三个(或三个以上)的数的大小比较,则应先根据值的大小(特别是与 0、1 大小)进行分组,再比较各组数的大小即可.
失误防范
求函数的值域时一定要考虑定义域,否则易出错.本部分内容讲解结束按ESC键退出全屏播放
