华东师大版数学九年级上册 23.4 中位线 课件(共17张PPT)
文档属性
| 名称 | 华东师大版数学九年级上册 23.4 中位线 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 240.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-04 20:11:28 | ||
图片预览

文档简介
(共17张PPT)
23.4 中位线
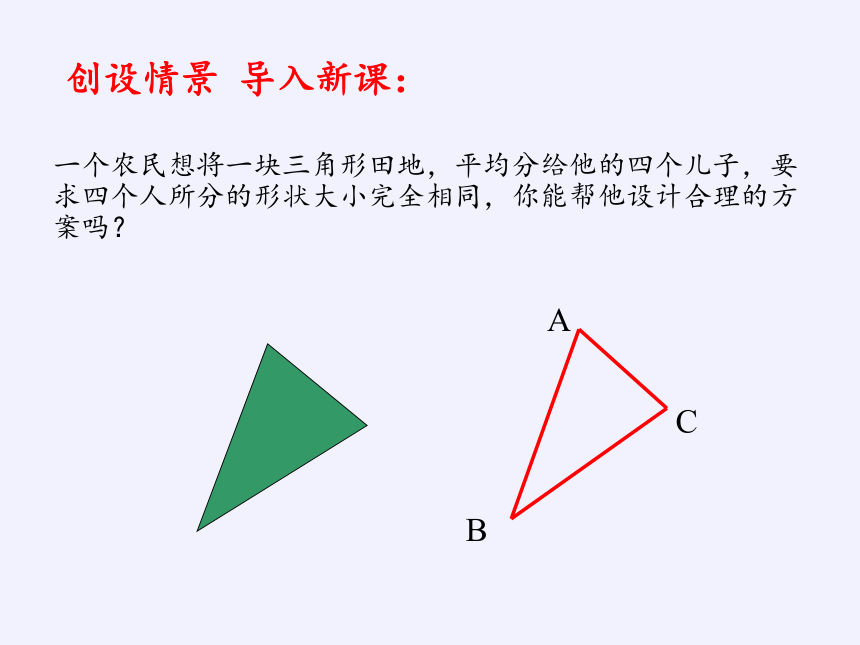
创设情景 导入新课:
一个农民想将一块三角形田地,平均分给他的四个儿子,要求四个人所分的形状大小完全相同,你能帮他设计合理的方案吗?
C
B
A
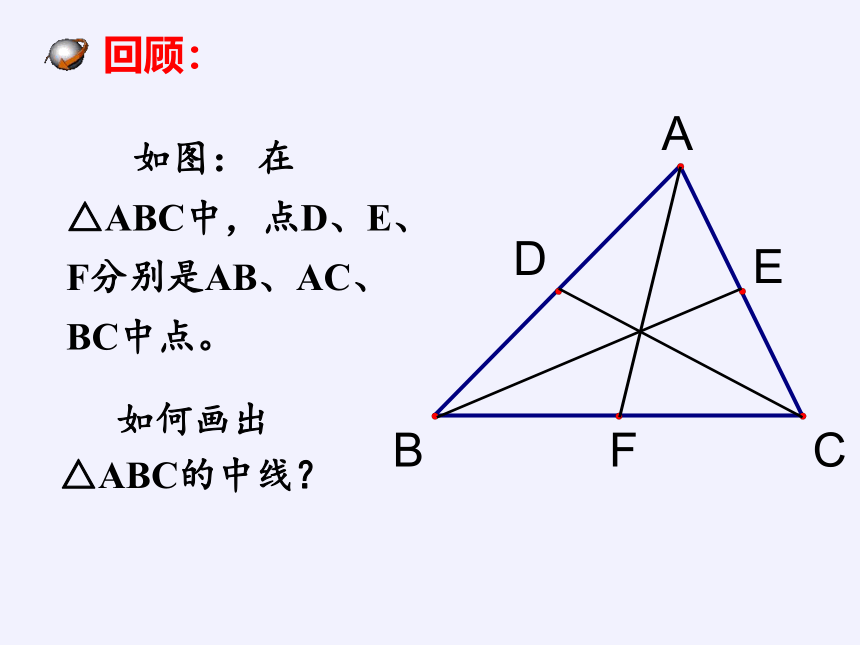
如图: 在△ABC中,点D、E、F分别是AB、AC、BC中点。
回顾:
如何画出△ABC的中线?
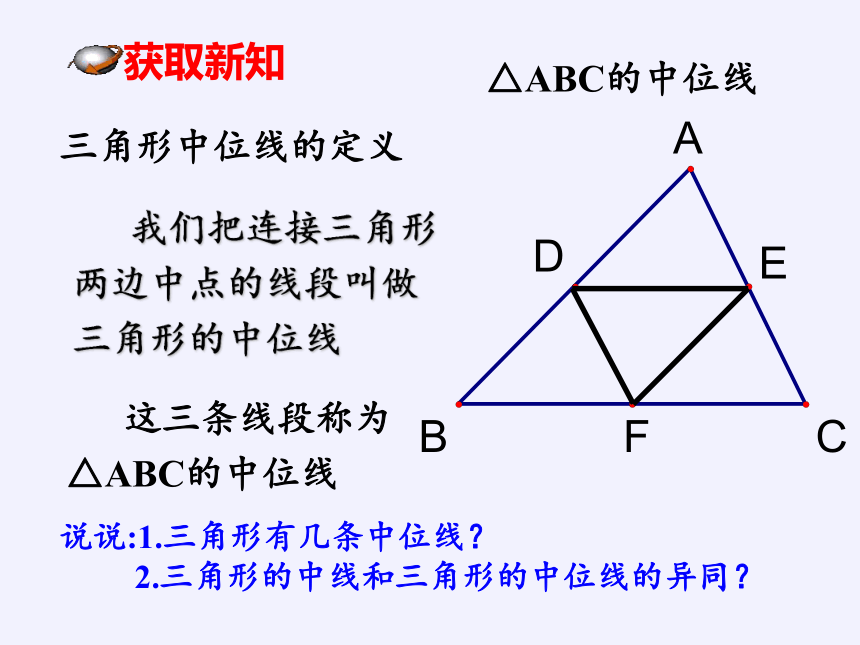
△ABC的中位线
这三条线段称为△ABC的中位线
三角形中位线的定义
我们把连接三角形两边中点的线段叫做三角形的中位线
获取新知
说说:1.三角形有几条中位线?
2.三角形的中线和三角形的中位线的异同?
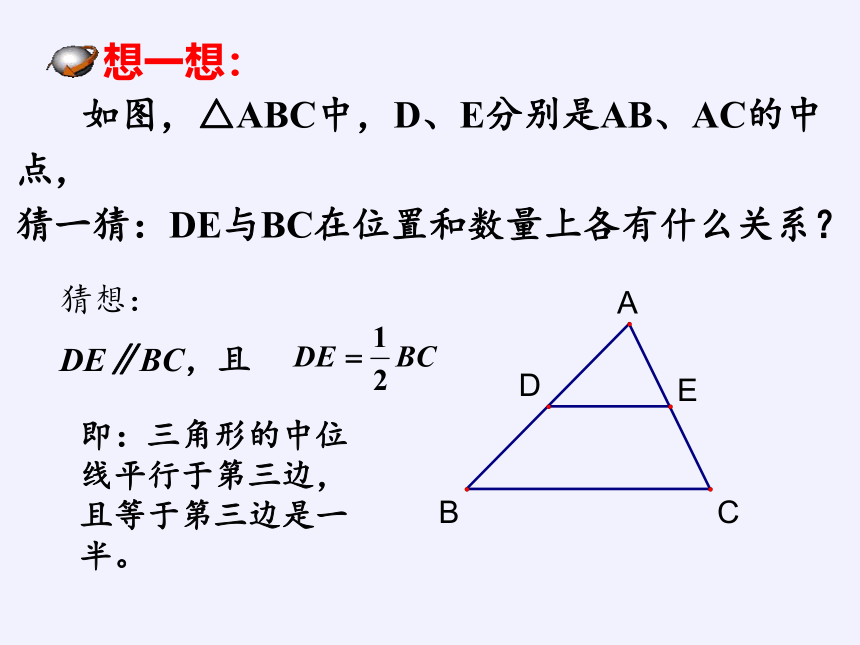
如图,△ABC中,D、E分别是AB、AC的中点,
猜一猜:DE与BC在位置和数量上各有什么关系?
想一想:
猜想:
DE∥BC,且
即:三角形的中位线平行于第三边,且等于第三边是一半。
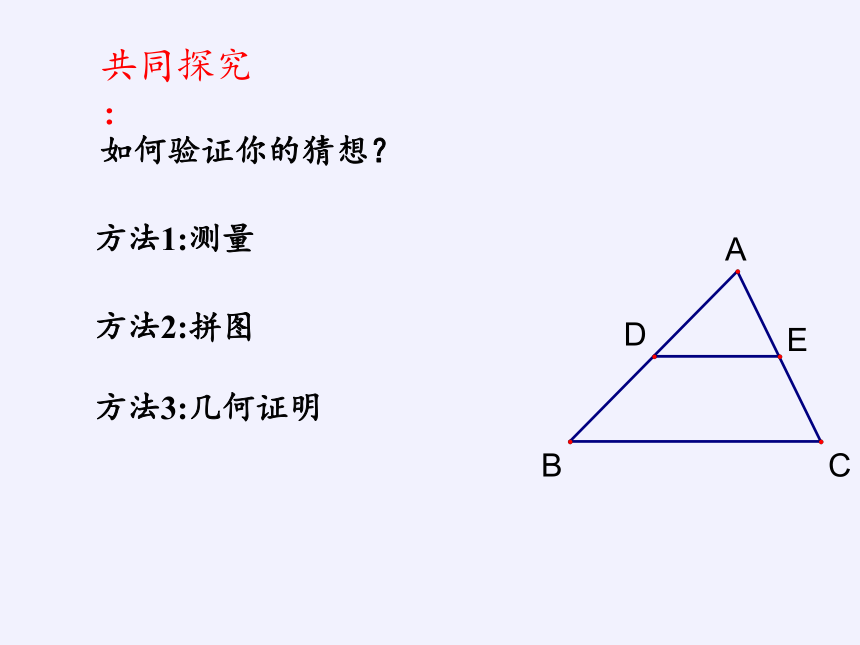
如何验证你的猜想?
共同探究:
方法1:测量
方法2:拼图
方法3:几何证明
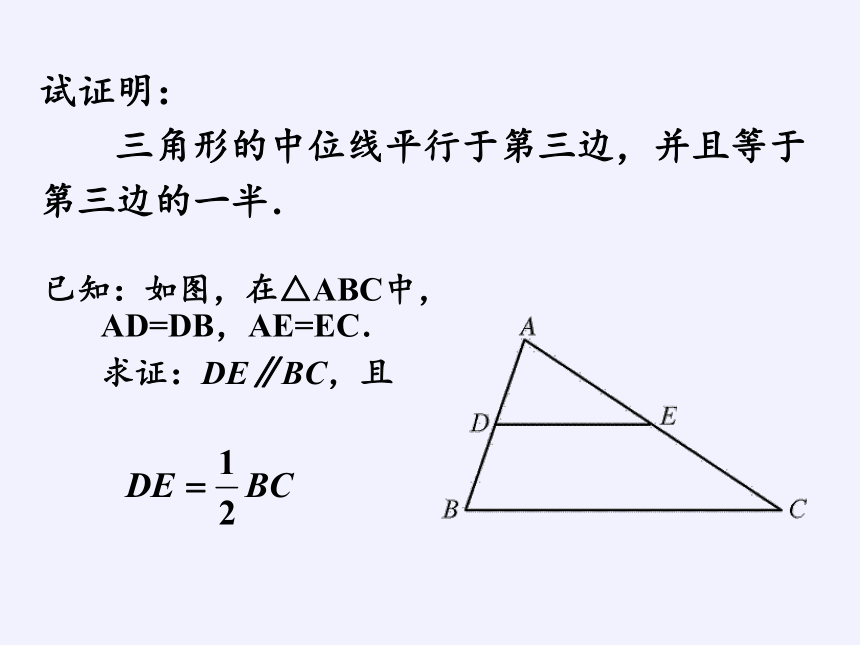
试证明:
三角形的中位线平行于第三边,并且等于第三边的一半.
已知:如图,在△ABC中,AD=DB,AE=EC.
求证:DE∥BC,且
DE∥BC,DE= BC
.
已知:如图,在△ABC中,AD=DB,AE=EC.
求证:
三角形的中位线性质:
三角形的中位线平行于第三边,且等于第三边是一半。
在△ABC中,∵AD=DB,AE=EC.
∴DE= BC,
几何语言:
∥
2
1
1.已知:如果,点D、E、F分别是△ABC的三边的中点.
(1)若AB=8cm,求EF的长;
(2)若DE=5cm,求BC的长.
(3)若增加M、N分别是BD、BF的中点,
问:MN与AC有什么关系?
为什么?
M
N
试一试:
2.如图1: 在△ABC中,点D、E、分别是AB、AC中点。若AB=6,AC=4,BC=8,则△ADE的周长为 ?
3.如图2: 在△ABC中,点D、E、F分别是AB、AC、BC中点。若△ABC的周长为24,面积为16 ,则△DEF的周长为 ?面积为
图1
图2
F
三角形三条中线围成的三角形的周长与原周长有什么关系?面积有与原面积什么关系?
探究:
9
4
12
结论:
如果三角形的周长为C,那么顺次连接各边中点所得的三角形周长为
如果角形的面积为S,那么顺次连接各边中点所得的三角形面积为
2
1
C
4
1
S
设计方案:
E(中点)
F(中点)
(中点)D
C
A
B
4.已知:如图,在△ABC中, AD=DB,BE=EC, AF=FC
求证:AE、DF互相平分
思考:
A
B
D
C
E
F
证明 连结DE、EF.
∵ AD=DB,BE=EC,
∴ DE∥AC(三角形的中位线平行于第三边并且等于第三边的一半).
同理EF∥AB.
∴四边形ADEF是平行四边形.
∴ AE、DF互相平分(平行四边形的对角线互相平分).
2.三角形的中位线性质:
三角形的中位线平行与第三边且等于第三边的一半.
小结
1.三角形的中位线定义:
连接三角形两边中点的线段叫做三角形的中位线。
谢 谢
23.4 中位线
创设情景 导入新课:
一个农民想将一块三角形田地,平均分给他的四个儿子,要求四个人所分的形状大小完全相同,你能帮他设计合理的方案吗?
C
B
A
如图: 在△ABC中,点D、E、F分别是AB、AC、BC中点。
回顾:
如何画出△ABC的中线?
△ABC的中位线
这三条线段称为△ABC的中位线
三角形中位线的定义
我们把连接三角形两边中点的线段叫做三角形的中位线
获取新知
说说:1.三角形有几条中位线?
2.三角形的中线和三角形的中位线的异同?
如图,△ABC中,D、E分别是AB、AC的中点,
猜一猜:DE与BC在位置和数量上各有什么关系?
想一想:
猜想:
DE∥BC,且
即:三角形的中位线平行于第三边,且等于第三边是一半。
如何验证你的猜想?
共同探究:
方法1:测量
方法2:拼图
方法3:几何证明
试证明:
三角形的中位线平行于第三边,并且等于第三边的一半.
已知:如图,在△ABC中,AD=DB,AE=EC.
求证:DE∥BC,且
DE∥BC,DE= BC
.
已知:如图,在△ABC中,AD=DB,AE=EC.
求证:
三角形的中位线性质:
三角形的中位线平行于第三边,且等于第三边是一半。
在△ABC中,∵AD=DB,AE=EC.
∴DE= BC,
几何语言:
∥
2
1
1.已知:如果,点D、E、F分别是△ABC的三边的中点.
(1)若AB=8cm,求EF的长;
(2)若DE=5cm,求BC的长.
(3)若增加M、N分别是BD、BF的中点,
问:MN与AC有什么关系?
为什么?
M
N
试一试:
2.如图1: 在△ABC中,点D、E、分别是AB、AC中点。若AB=6,AC=4,BC=8,则△ADE的周长为 ?
3.如图2: 在△ABC中,点D、E、F分别是AB、AC、BC中点。若△ABC的周长为24,面积为16 ,则△DEF的周长为 ?面积为
图1
图2
F
三角形三条中线围成的三角形的周长与原周长有什么关系?面积有与原面积什么关系?
探究:
9
4
12
结论:
如果三角形的周长为C,那么顺次连接各边中点所得的三角形周长为
如果角形的面积为S,那么顺次连接各边中点所得的三角形面积为
2
1
C
4
1
S
设计方案:
E(中点)
F(中点)
(中点)D
C
A
B
4.已知:如图,在△ABC中, AD=DB,BE=EC, AF=FC
求证:AE、DF互相平分
思考:
A
B
D
C
E
F
证明 连结DE、EF.
∵ AD=DB,BE=EC,
∴ DE∥AC(三角形的中位线平行于第三边并且等于第三边的一半).
同理EF∥AB.
∴四边形ADEF是平行四边形.
∴ AE、DF互相平分(平行四边形的对角线互相平分).
2.三角形的中位线性质:
三角形的中位线平行与第三边且等于第三边的一半.
小结
1.三角形的中位线定义:
连接三角形两边中点的线段叫做三角形的中位线。
谢 谢
