华东师大版数学九年级上册 24.4 解直角三角形 课件(共17张PPT)
文档属性
| 名称 | 华东师大版数学九年级上册 24.4 解直角三角形 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-04 20:12:42 | ||
图片预览





文档简介
(共16张PPT)
解直角三角形
在直角三角形中,除直角外的已知元素求出所有未知元素的过程叫做解直角三角形。
复习回顾
1、解直角三角形
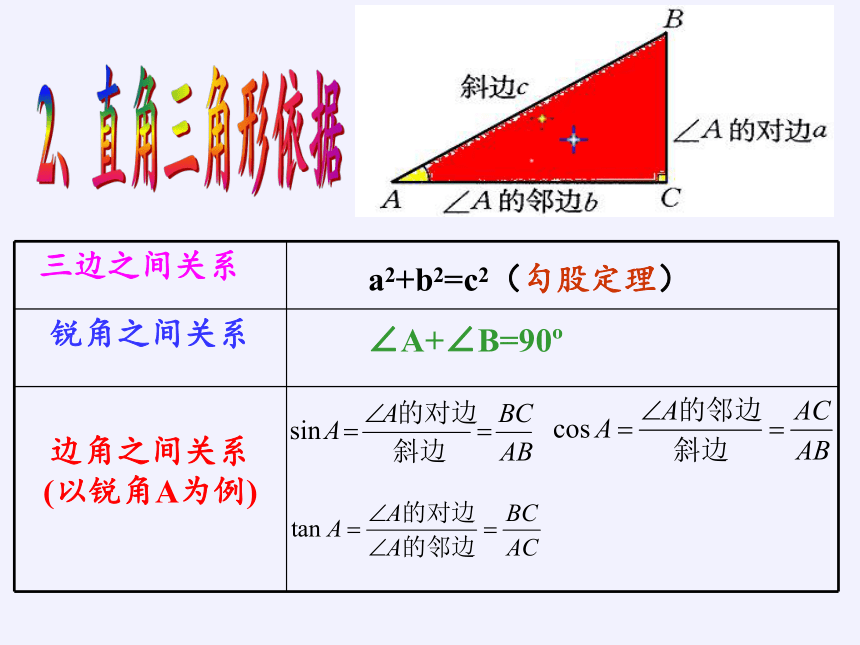
三边之间关系
锐角之间关系
边角之间关系 (以锐角A为例)
a2+b2=c2(勾股定理)
∠A+∠B=90
2、直角三角形依据
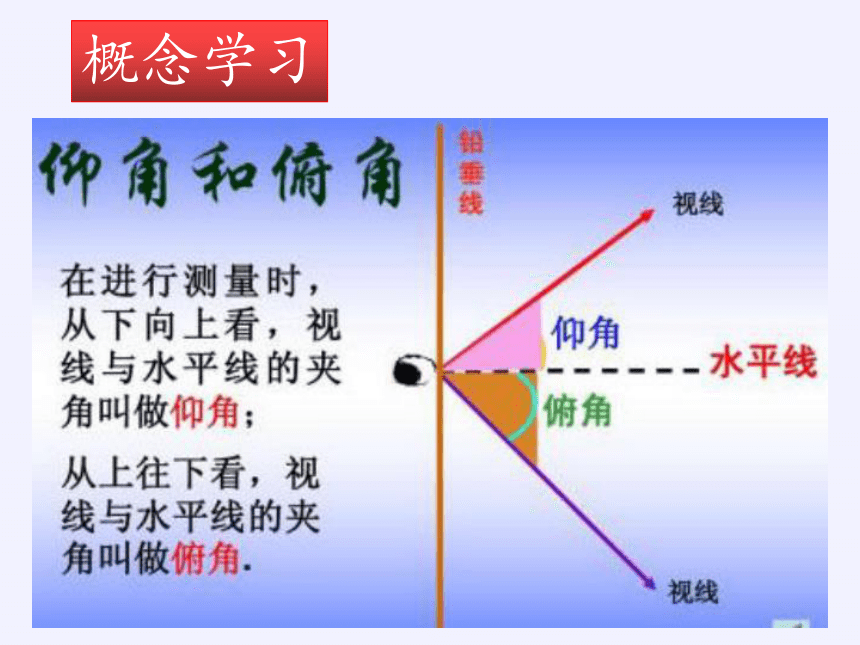
仰角
知识实用性
概念学习
1200
2400
Sin sin30
AC
AB
B
= =
o
创设情境 导入新课
例1:如图,某敌机我国领空飞过,此时探测敌机飞行高度为AC=1200米,若从B处发射地对空导弹,以仰角α=300发射,试求发射点B到飞机A的距离.(精确到1米)
α
A
B
C
α
C
B
A
解 在Rt△ABC中,∠ B =α
答:飞机A到控制点B的距离约2400米
)30°
解 在Rt△CDE中,α=52°
CE=DE×tanα
=AB×tanα
=10×tan 52°
≈12.80
BC=BE+CE
=DA+CD
=1.50+12.80
≈14.3(米)
答:旗杆BC的高度约为14.3米.
∵
∴
例2、如图,为了测量旗杆的高度BC,在离旗杆10米的A处,C用高1.50米的测角仪DA测得旗杆顶端C的仰角α=52°,求旗杆BC的高.(tan52°=1.2799;结果精确到0.1米)
10m
52°
练习
1、如图4,为测量某物体AB的高度,在D点测得A
点的仰角为30°,朝物体AB方向前进100m到达
点C,再次测得A点的仰角为60°,则物体AB的
高度为:
水平线
地面
2、如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看地平面控制点B的俯角 =370,求飞机A到控制点B的距离。(Sin37°≈0.6)
练习
解 在Rt△ABC中, AC=1200, =370
由
所以
AB=
1200
Sin37°
所以飞机A到控制点B的距离约2000米.
AB=
1200
0.6
AB=2000(米)
2、如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看地平面控制点B的俯角 =370,求飞机A到控制点B的距离。(Sin37°≈0.6)
37°
1200m
3、小玲家对面新造了一幢图书大厦,小玲在自家窗口测得大厦顶部的仰角和大厦底部的俯角(如图所示),量得两幢楼之间的距离为30m,问大厦有多高?
30m
小玲家
解:在ΔABC中,∠ACB =900
∵ ∠CAB =450
∴
在ΔADC中 ∠ACD=900
∵ ∠CAD=300
30m
AC=30m
答:大厦高BD约为51m.
AC=30m
30
tan
×
o
∴
=
AC
DC
小结
1.学习了俯角、仰角的概念,明确各术语与示意图中的什么元素对应,只有明确这些概念,才能恰当地把实际问题转化为数学问题
2.认真分析题意、将实际问题转化并构造直角三角形来解决.
3.选择合适的边角关系式,运用勾股定理或三角函数等相关知识点解决问题。
祝学习进步
课本P114练习1,第2题 。
完成同步练习册P97
第三题1、2
作业
谢 谢
解直角三角形
在直角三角形中,除直角外的已知元素求出所有未知元素的过程叫做解直角三角形。
复习回顾
1、解直角三角形
三边之间关系
锐角之间关系
边角之间关系 (以锐角A为例)
a2+b2=c2(勾股定理)
∠A+∠B=90
2、直角三角形依据
仰角
知识实用性
概念学习
1200
2400
Sin sin30
AC
AB
B
= =
o
创设情境 导入新课
例1:如图,某敌机我国领空飞过,此时探测敌机飞行高度为AC=1200米,若从B处发射地对空导弹,以仰角α=300发射,试求发射点B到飞机A的距离.(精确到1米)
α
A
B
C
α
C
B
A
解 在Rt△ABC中,∠ B =α
答:飞机A到控制点B的距离约2400米
)30°
解 在Rt△CDE中,α=52°
CE=DE×tanα
=AB×tanα
=10×tan 52°
≈12.80
BC=BE+CE
=DA+CD
=1.50+12.80
≈14.3(米)
答:旗杆BC的高度约为14.3米.
∵
∴
例2、如图,为了测量旗杆的高度BC,在离旗杆10米的A处,C用高1.50米的测角仪DA测得旗杆顶端C的仰角α=52°,求旗杆BC的高.(tan52°=1.2799;结果精确到0.1米)
10m
52°
练习
1、如图4,为测量某物体AB的高度,在D点测得A
点的仰角为30°,朝物体AB方向前进100m到达
点C,再次测得A点的仰角为60°,则物体AB的
高度为:
水平线
地面
2、如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看地平面控制点B的俯角 =370,求飞机A到控制点B的距离。(Sin37°≈0.6)
练习
解 在Rt△ABC中, AC=1200, =370
由
所以
AB=
1200
Sin37°
所以飞机A到控制点B的距离约2000米.
AB=
1200
0.6
AB=2000(米)
2、如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看地平面控制点B的俯角 =370,求飞机A到控制点B的距离。(Sin37°≈0.6)
37°
1200m
3、小玲家对面新造了一幢图书大厦,小玲在自家窗口测得大厦顶部的仰角和大厦底部的俯角(如图所示),量得两幢楼之间的距离为30m,问大厦有多高?
30m
小玲家
解:在ΔABC中,∠ACB =900
∵ ∠CAB =450
∴
在ΔADC中 ∠ACD=900
∵ ∠CAD=300
30m
AC=30m
答:大厦高BD约为51m.
AC=30m
30
tan
×
o
∴
=
AC
DC
小结
1.学习了俯角、仰角的概念,明确各术语与示意图中的什么元素对应,只有明确这些概念,才能恰当地把实际问题转化为数学问题
2.认真分析题意、将实际问题转化并构造直角三角形来解决.
3.选择合适的边角关系式,运用勾股定理或三角函数等相关知识点解决问题。
祝学习进步
课本P114练习1,第2题 。
完成同步练习册P97
第三题1、2
作业
谢 谢
