华东师大版数学九年级上册 23.3.1 相似三角形 课件(共20张PPT)
文档属性
| 名称 | 华东师大版数学九年级上册 23.3.1 相似三角形 课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-05 09:09:53 | ||
图片预览






文档简介
(共20张PPT)
相似三角形
5
8
7
94
40
46
20
32
28
94
40
46
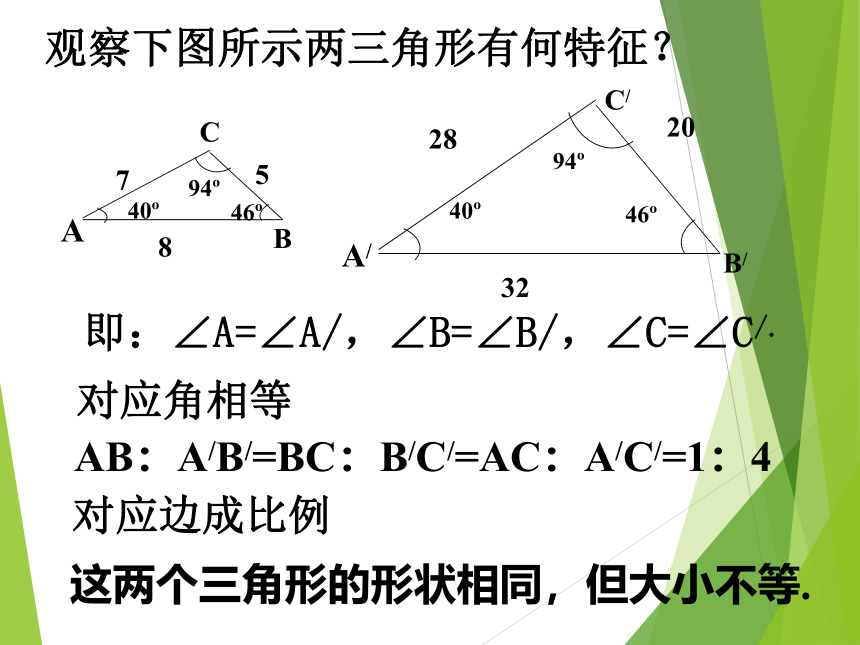
观察下图所示两三角形有何特征?
A/
A
B/
B
C/
C
即:∠A=∠A/,∠B=∠B/,∠C=∠C/.
AB:A/B/=BC:B/C/=AC:A/C/=1:4
对应角相等
对应边成比例
这两个三角形的形状相同,但大小不等.
对应角相等、对应边成比例的两个三角形叫做相似三角形。 ABC与 DEF相似,记作 ABC ∽ DEF。
相似三角形
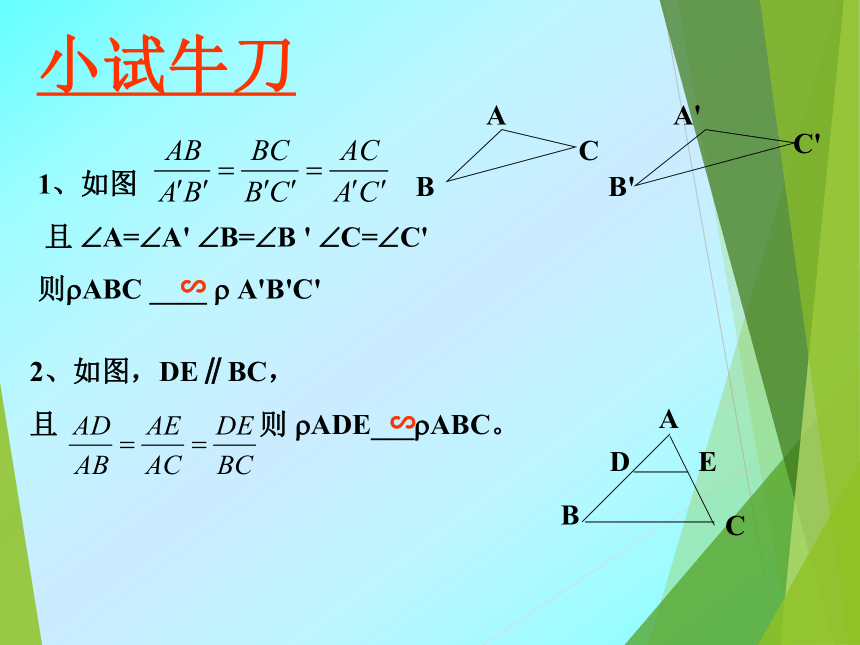
1、如图
且 A= A' B= B ' C= C'
则 ABC ____ A'B'C'
2、如图,DE∥BC,
且 则 ADE___ ABC。
B
A
C
B'
A'
C'
A
B
C
D
E
小试牛刀
∽
∽
由上面 结论完成下列各题:
1、若 ABC∽ DEF, 则 A=____,
____= E, C= ____,
2、若 A1B1C1 ∽ A2B2C2 ,且A1C1 =2,A2C2 =6,
则 A1B1C1 与 A2B2C2 的相似比是_____。
如果 ABC∽ DEF,那么哪些角是对应角?哪些边是对应边?对应角有什么关系 ?对应边呢?什么是相似比?
相似三角形对应角相等,对应边成比例。对应边的比为相似比。
∠D
∠B
∠F
DE
AC
EF
想 一想
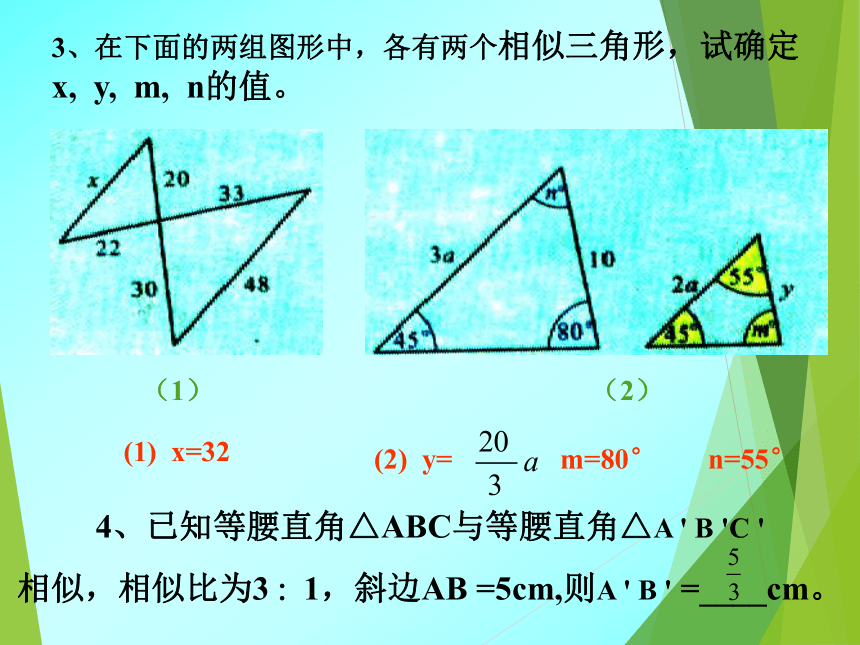
4、已知等腰直角△ABC与等腰直角△A ' B 'C '
相似,相似比为3 1,斜边AB =5cm,则A ' B ' =____cm。
3、在下面的两组图形中,各有两个相似三角形,试确定 x, y, m, n的值。
(1)
(2)
(1) x=32
(2) y= m=80° n=55°
(1)两个全等三角形一定相似吗?为什么?
(2)两个直角三角形一定相似吗?两个等腰
直角三角形呢?为什么?
(3)两个等腰三角形一定相似吗?两个等边
三角形呢?为什么?
议一议:
实践应用:
例1 、如图,有一块三角形形状的草坪,其中一边的长是20m。在这个草坪的图纸上,这条边长5cm,其他两边的长都是3 5cm,求该草坪其他两边的实际长度。
解:草坪的形状与其图纸上相应的形状相似,他们的相似比是 2000:5=400:1
如果设其他两边的实际长度都是x cm,那么
x=3.5×400=1400(cm)
1400cm=14m
所以草坪其他两边的实际长度都是14m。
5cm
3.5cm
3.5cm
20m
练一练,你会了吗?
1、有 一块三角形形状的土地 ,其中最长一边长20m ,在这块土地的 图纸上,这三边分别长5cm,2cm,4cm,则该土地其他两边的实际长度 分别为______、______。
2、已知 ABC ∽ A ‘ B ’C ‘ , 若 ABC三边长分别为3,4,5,则 A ’ B ‘C ’ 的形状 是__________,若 A ‘ B ’C ‘的最长边为15,则 S A ’ B ‘C ’ = _____。
8m
16m
直角三角形
54
例2 如图,已知 ABC ∽ ADE,AE=50,EC=30,
BC=70, BAC=45°, ACB=40°。
(1)求 AED和 ADE的大小;
(2)求DE的长。
解:(1)因为 ABC ∽ ADE,
所以由相似三角形对应角相等,得
AED= ACB=40°。在 ADE中, AED+ ADE+ A=180°
所以 ADE=180°-40°-45°=95°
(2)因为 ABC ∽ ADE,所以由相似三角形对应边 成比
例,得 即
A
E
D
C
B
50
30
70
所以 DE=43.75
想一想:
在例2的条件下图中有哪些线段成比例?图中有互相平行的线段吗?
A
E
D
C
B
1、已知:如图AB是斜靠的长梯,
梯脚B距墙根C1 6米,梯上点D距离
墙1 4米,已知BD=0.5米,且
ADE∽ ABC,那么
AD=_____米,梯子的长度
为______米。
2、如图,已知 ADE∽ ABC,
AB=10,AD=6,BC=12, A=56°,
ADE=40°,则 ACB=____度,
DE=_____。
A
D
B
E
C
A
E
B
D
C
4
3.5
54
7.2
跟踪练习:
例3:如图,在△ABC中,DE∥BC,D,E分别在AB,AC上,求证:△ADE∽△ABC
F
证明:在△ADE和△ABC中,∠A=∠A,∵DE∥BC∴∠ADE=∠B∠AED=∠C,
过点E作EF∥AB,交BC于F,
则四边形BFED是平行四边形。
∴DE=BF.又∵EF∥AB,
∴
∴
∴
△ADE∽△ABC
相似三角形判定预备定理:
平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。
A型图
X型图
练习:如图D为△ABC的边AC上一点,过点D作DE∥AB,交BC于E.已知
BE:EC=1:2,AB=6,求DE的长。
相似比k(对应边的比值)
k 1 两三角形形状 相同而大小不同 k=1 两三角形全等
课堂小结
对应角相等
对应边成比例
定义
表示法
“ ∽”
相似三角形
相似三角形判定预备定理:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.
1、若 ABC∽ A ' B 'C ',相似比为k (k 1),则k的值应是( )
(A) A: A' (B)BC : B ' C ' (C) A ' : A (D)A ' B ' : AB
2、若两个相似三角形的相似比为1,则这两个三角形必________.
3、已知 ABC∽ A ' B ' C ',如果 A=55° , B=100°,则
C'=_______.
4、已知 ABC∽ A ' B ' C '且相似比k= ,若AB=10,
则A ' B ' =______.
5 、已知 A1B1C1 与 A2B2C2 的相似比是k,则 A2B2C2与 A1B1C1
的相似比是________.
B
全等
25°
20
7、 ABC的三边长分别为 、 、2,
A B C 的两边长为 1和 ,若
ABC ∽ A B C ,则 A B C 的第三边长应为_____。
6、如图, ABO ∽ CDO则AB与CD的位置
关系是_________。
A
B
C
D
O
AB ∥ CD
ABC ∽ DEF若 ABC的三边长分别为5cm、6cm、7cm、而4cm是 DEF中一边的长度,你能求出 DEF的另外两边的长度吗?试说明理由。
谢谢大家
再见
相似三角形
5
8
7
94
40
46
20
32
28
94
40
46
观察下图所示两三角形有何特征?
A/
A
B/
B
C/
C
即:∠A=∠A/,∠B=∠B/,∠C=∠C/.
AB:A/B/=BC:B/C/=AC:A/C/=1:4
对应角相等
对应边成比例
这两个三角形的形状相同,但大小不等.
对应角相等、对应边成比例的两个三角形叫做相似三角形。 ABC与 DEF相似,记作 ABC ∽ DEF。
相似三角形
1、如图
且 A= A' B= B ' C= C'
则 ABC ____ A'B'C'
2、如图,DE∥BC,
且 则 ADE___ ABC。
B
A
C
B'
A'
C'
A
B
C
D
E
小试牛刀
∽
∽
由上面 结论完成下列各题:
1、若 ABC∽ DEF, 则 A=____,
____= E, C= ____,
2、若 A1B1C1 ∽ A2B2C2 ,且A1C1 =2,A2C2 =6,
则 A1B1C1 与 A2B2C2 的相似比是_____。
如果 ABC∽ DEF,那么哪些角是对应角?哪些边是对应边?对应角有什么关系 ?对应边呢?什么是相似比?
相似三角形对应角相等,对应边成比例。对应边的比为相似比。
∠D
∠B
∠F
DE
AC
EF
想 一想
4、已知等腰直角△ABC与等腰直角△A ' B 'C '
相似,相似比为3 1,斜边AB =5cm,则A ' B ' =____cm。
3、在下面的两组图形中,各有两个相似三角形,试确定 x, y, m, n的值。
(1)
(2)
(1) x=32
(2) y= m=80° n=55°
(1)两个全等三角形一定相似吗?为什么?
(2)两个直角三角形一定相似吗?两个等腰
直角三角形呢?为什么?
(3)两个等腰三角形一定相似吗?两个等边
三角形呢?为什么?
议一议:
实践应用:
例1 、如图,有一块三角形形状的草坪,其中一边的长是20m。在这个草坪的图纸上,这条边长5cm,其他两边的长都是3 5cm,求该草坪其他两边的实际长度。
解:草坪的形状与其图纸上相应的形状相似,他们的相似比是 2000:5=400:1
如果设其他两边的实际长度都是x cm,那么
x=3.5×400=1400(cm)
1400cm=14m
所以草坪其他两边的实际长度都是14m。
5cm
3.5cm
3.5cm
20m
练一练,你会了吗?
1、有 一块三角形形状的土地 ,其中最长一边长20m ,在这块土地的 图纸上,这三边分别长5cm,2cm,4cm,则该土地其他两边的实际长度 分别为______、______。
2、已知 ABC ∽ A ‘ B ’C ‘ , 若 ABC三边长分别为3,4,5,则 A ’ B ‘C ’ 的形状 是__________,若 A ‘ B ’C ‘的最长边为15,则 S A ’ B ‘C ’ = _____。
8m
16m
直角三角形
54
例2 如图,已知 ABC ∽ ADE,AE=50,EC=30,
BC=70, BAC=45°, ACB=40°。
(1)求 AED和 ADE的大小;
(2)求DE的长。
解:(1)因为 ABC ∽ ADE,
所以由相似三角形对应角相等,得
AED= ACB=40°。在 ADE中, AED+ ADE+ A=180°
所以 ADE=180°-40°-45°=95°
(2)因为 ABC ∽ ADE,所以由相似三角形对应边 成比
例,得 即
A
E
D
C
B
50
30
70
所以 DE=43.75
想一想:
在例2的条件下图中有哪些线段成比例?图中有互相平行的线段吗?
A
E
D
C
B
1、已知:如图AB是斜靠的长梯,
梯脚B距墙根C1 6米,梯上点D距离
墙1 4米,已知BD=0.5米,且
ADE∽ ABC,那么
AD=_____米,梯子的长度
为______米。
2、如图,已知 ADE∽ ABC,
AB=10,AD=6,BC=12, A=56°,
ADE=40°,则 ACB=____度,
DE=_____。
A
D
B
E
C
A
E
B
D
C
4
3.5
54
7.2
跟踪练习:
例3:如图,在△ABC中,DE∥BC,D,E分别在AB,AC上,求证:△ADE∽△ABC
F
证明:在△ADE和△ABC中,∠A=∠A,∵DE∥BC∴∠ADE=∠B∠AED=∠C,
过点E作EF∥AB,交BC于F,
则四边形BFED是平行四边形。
∴DE=BF.又∵EF∥AB,
∴
∴
∴
△ADE∽△ABC
相似三角形判定预备定理:
平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。
A型图
X型图
练习:如图D为△ABC的边AC上一点,过点D作DE∥AB,交BC于E.已知
BE:EC=1:2,AB=6,求DE的长。
相似比k(对应边的比值)
k 1 两三角形形状 相同而大小不同 k=1 两三角形全等
课堂小结
对应角相等
对应边成比例
定义
表示法
“ ∽”
相似三角形
相似三角形判定预备定理:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.
1、若 ABC∽ A ' B 'C ',相似比为k (k 1),则k的值应是( )
(A) A: A' (B)BC : B ' C ' (C) A ' : A (D)A ' B ' : AB
2、若两个相似三角形的相似比为1,则这两个三角形必________.
3、已知 ABC∽ A ' B ' C ',如果 A=55° , B=100°,则
C'=_______.
4、已知 ABC∽ A ' B ' C '且相似比k= ,若AB=10,
则A ' B ' =______.
5 、已知 A1B1C1 与 A2B2C2 的相似比是k,则 A2B2C2与 A1B1C1
的相似比是________.
B
全等
25°
20
7、 ABC的三边长分别为 、 、2,
A B C 的两边长为 1和 ,若
ABC ∽ A B C ,则 A B C 的第三边长应为_____。
6、如图, ABO ∽ CDO则AB与CD的位置
关系是_________。
A
B
C
D
O
AB ∥ CD
ABC ∽ DEF若 ABC的三边长分别为5cm、6cm、7cm、而4cm是 DEF中一边的长度,你能求出 DEF的另外两边的长度吗?试说明理由。
谢谢大家
再见
