沪科版数学九年级上册 22.3 相似三角形的性质(课件)(共16张PPT)
文档属性
| 名称 | 沪科版数学九年级上册 22.3 相似三角形的性质(课件)(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 255.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-05 09:09:42 | ||
图片预览






文档简介
(共16张PPT)
22.3 相似三角形的性质
温故知新
相似三角形的性质定理
相似三角形性质定理1:相似三角形对应高的比,对应中线的比
和对应角平分线的比都等于相似比.
相似三角形性质定理2:相似三角形周长的比,等于相似比.
相似三角形性质定理3:相似三角形面积的比,等于相似比的平方.
4cm
1. 已知:△ABC∽△A B C ,BC=3.6cm,B C =6cm, AE
是△ABC的一条中线,AE=2.4cm, 则△A B C 中对应中
线A E 的长是 .
′
′
′
′
′
′
′
′
′
′
温故知新
2.已知△ABC和△DEF的面积比是9∶4,则△ABC和△DEF
的相似比是 .
3∶2
3.如果两个相似三角形的周长分别是1和4,那么这两个三角
形的面积之比是 .
1∶16
相似三角形周长的比=对应高的比=对应中线的比
=对应角平分线的比=相似比(对应边的比).
相似三角形的相似比等于面积比的算术平方根.
例题解析
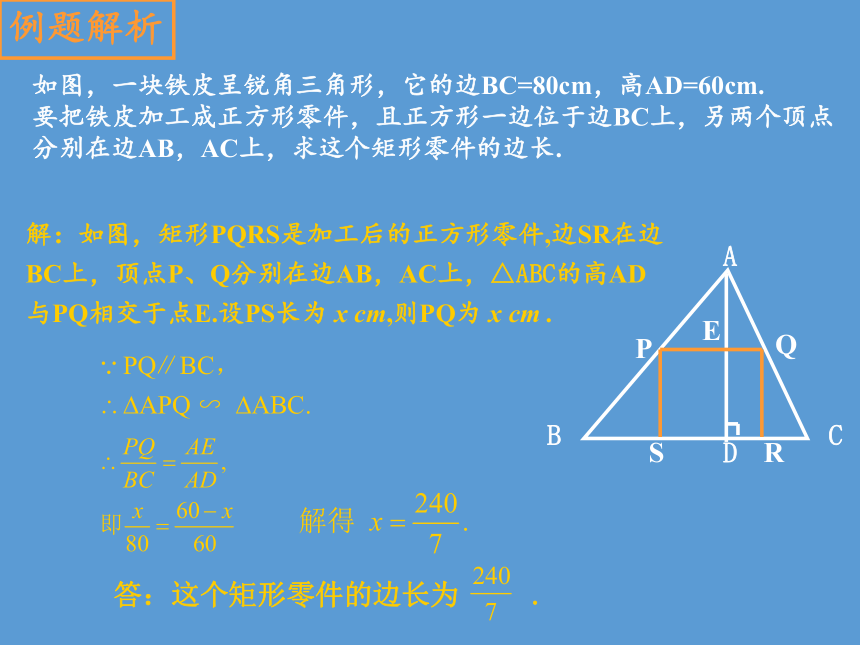
如图,一块铁皮呈锐角三角形,它的边BC=80cm,高AD=60cm.
要把铁皮加工成正方形零件,且正方形一边位于边BC上,另两个顶点
分别在边AB,AC上,求这个矩形零件的边长.
解:如图,矩形PQRS是加工后的正方形零件,边SR在边BC上,顶点P、Q分别在边AB,AC上,△ABC的高AD与PQ相交于点E.设PS长为 x cm,则PQ为 x cm .
E
P
Q
S
R
D
B
A
C
答:这个矩形零件的边长为 .
拓展延伸
(变式1)如图,一块铁皮呈锐角三角形,它的边BC=80cm,高AD=60cm.要把铁皮加工成矩形零件,使矩形的两边之比是2:1,且矩形的一边位于边BC上,另两个顶点分别在边AB,AC上,求这个矩形零件的边长.
B
A
C
D
[解析]
条件中没有指明矩形的哪一边位于边BC上,
有可能是长,也有可能是宽,所以有两种方案.
拓展延伸
方案(1)矩形长的一边位于边BC上.
解:如图,矩形PQRS是加工后的矩形零件,边SR在边BC上,顶点P、Q分别在边AB,AC上,△ABC的高AD与PQ相交于点E.设PS长为x cm,则PQ为2x cm .
B
A
C
D
E
P
Q
S
R
答:这个矩形零件的边长分别为48cm和24cm.
拓展延伸
B
A
D
C
E
P
Q
S
R
解:如图,矩形PQRS是加工后的矩形零件,边SR在边BC上,顶点P、Q分别在边AB,AC上,△ABC的高AD与PQ相交于点E.设PQ长为x cm,则PS为2x cm .
答:这个矩形零件的边长分别为 cm和 cm.
方案(2)矩形短的一边位于边BC上.
(变式2)一块铁皮呈直角三角形,直角边AB=1.5cm,面积为1.5m .
现要把它加工成一个面积最大的正方形零件,有甲乙两种加工方案:
分别如图①,图②.你认为哪种设计
方案好?试着说明理由.(加工损耗忽略不计)
拓展延伸
图①
D
B
C
A
E
图②
D
C
B
A
E
G
F
[解析] 利用正方形的对边平行寻找相似三角形,由“相似三角形对应边的比等于对应边上高的比”的性质,列出等量关系式,计算正方形的边长x、y,比较大小,选择合理方案.
解决此问题的关键是在正确理解题意的基础上建立数学模型,把实际问题转化为数学问题.利用相似三角形对应边上的高之比等于对应边之比列方程求解.
B
A
C
D
E
P
Q
S
R
B
A
D
C
E
P
Q
S
R
图①
D
B
C
A
E
图②
D
C
B
A
E
G
F
归 纳
如图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.
若测得BD=120米,DC=60米,EC=50米,求两岸间距离AB.
A
D
E
B
C
测量应用
解: ∵ AB ∥CE ,∴△ABD ∽△ECD,
答:两岸间距离100米.
我们还可以在河对岸选定一目标点A,再在河的一边选点D和 E,使DE⊥AD,然后,再选点B,作BC∥DE,与视线EA相交于点C。此时,测得DE , BC, BD, 就可以求两岸间的大致距离AB了。
A
D
E
B
C
你能解释此方案的合理性吗?
测量应用
(变式) 有一条河的两岸某一段是平行的,在该河岸的这一段每隔5米有一棵树,河的对岸每隔50米有一电线杆,在河岸离开岸边25米处看对岸,看到对岸相邻的两根电线杆恰好被河岸的两棵树遮住,且这两棵树之间还有3棵树,求河宽.
[解析] 依据题意画出示意图,人站在A处,D,E为对岸的两电线杆,B,C为这岸的两棵树,且B,C之间还有3棵树,AM为人到这岸的距离,DE=50米,BC=20米,AM⊥BC,且AM=25米.
测量应用
解:如图,由BC∥DE可得△ABC∽△ADE.
[归纳] 本题利用相似三角形的性质解决实际问题,关键是画出图形,建立相似三角形的模型.
测量应用
小结
实际问题转化为数学模型
“转化”思想
应用相似三角形的性质解决实际问题时(如测量问题),
一般分为以下三个步骤:
①审题 ②构建图形 ③利用相似解决问题
作业
课本 P90页:
习题22.3:题 10、11、12、13.
谢 谢
22.3 相似三角形的性质
温故知新
相似三角形的性质定理
相似三角形性质定理1:相似三角形对应高的比,对应中线的比
和对应角平分线的比都等于相似比.
相似三角形性质定理2:相似三角形周长的比,等于相似比.
相似三角形性质定理3:相似三角形面积的比,等于相似比的平方.
4cm
1. 已知:△ABC∽△A B C ,BC=3.6cm,B C =6cm, AE
是△ABC的一条中线,AE=2.4cm, 则△A B C 中对应中
线A E 的长是 .
′
′
′
′
′
′
′
′
′
′
温故知新
2.已知△ABC和△DEF的面积比是9∶4,则△ABC和△DEF
的相似比是 .
3∶2
3.如果两个相似三角形的周长分别是1和4,那么这两个三角
形的面积之比是 .
1∶16
相似三角形周长的比=对应高的比=对应中线的比
=对应角平分线的比=相似比(对应边的比).
相似三角形的相似比等于面积比的算术平方根.
例题解析
如图,一块铁皮呈锐角三角形,它的边BC=80cm,高AD=60cm.
要把铁皮加工成正方形零件,且正方形一边位于边BC上,另两个顶点
分别在边AB,AC上,求这个矩形零件的边长.
解:如图,矩形PQRS是加工后的正方形零件,边SR在边BC上,顶点P、Q分别在边AB,AC上,△ABC的高AD与PQ相交于点E.设PS长为 x cm,则PQ为 x cm .
E
P
Q
S
R
D
B
A
C
答:这个矩形零件的边长为 .
拓展延伸
(变式1)如图,一块铁皮呈锐角三角形,它的边BC=80cm,高AD=60cm.要把铁皮加工成矩形零件,使矩形的两边之比是2:1,且矩形的一边位于边BC上,另两个顶点分别在边AB,AC上,求这个矩形零件的边长.
B
A
C
D
[解析]
条件中没有指明矩形的哪一边位于边BC上,
有可能是长,也有可能是宽,所以有两种方案.
拓展延伸
方案(1)矩形长的一边位于边BC上.
解:如图,矩形PQRS是加工后的矩形零件,边SR在边BC上,顶点P、Q分别在边AB,AC上,△ABC的高AD与PQ相交于点E.设PS长为x cm,则PQ为2x cm .
B
A
C
D
E
P
Q
S
R
答:这个矩形零件的边长分别为48cm和24cm.
拓展延伸
B
A
D
C
E
P
Q
S
R
解:如图,矩形PQRS是加工后的矩形零件,边SR在边BC上,顶点P、Q分别在边AB,AC上,△ABC的高AD与PQ相交于点E.设PQ长为x cm,则PS为2x cm .
答:这个矩形零件的边长分别为 cm和 cm.
方案(2)矩形短的一边位于边BC上.
(变式2)一块铁皮呈直角三角形,直角边AB=1.5cm,面积为1.5m .
现要把它加工成一个面积最大的正方形零件,有甲乙两种加工方案:
分别如图①,图②.你认为哪种设计
方案好?试着说明理由.(加工损耗忽略不计)
拓展延伸
图①
D
B
C
A
E
图②
D
C
B
A
E
G
F
[解析] 利用正方形的对边平行寻找相似三角形,由“相似三角形对应边的比等于对应边上高的比”的性质,列出等量关系式,计算正方形的边长x、y,比较大小,选择合理方案.
解决此问题的关键是在正确理解题意的基础上建立数学模型,把实际问题转化为数学问题.利用相似三角形对应边上的高之比等于对应边之比列方程求解.
B
A
C
D
E
P
Q
S
R
B
A
D
C
E
P
Q
S
R
图①
D
B
C
A
E
图②
D
C
B
A
E
G
F
归 纳
如图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.
若测得BD=120米,DC=60米,EC=50米,求两岸间距离AB.
A
D
E
B
C
测量应用
解: ∵ AB ∥CE ,∴△ABD ∽△ECD,
答:两岸间距离100米.
我们还可以在河对岸选定一目标点A,再在河的一边选点D和 E,使DE⊥AD,然后,再选点B,作BC∥DE,与视线EA相交于点C。此时,测得DE , BC, BD, 就可以求两岸间的大致距离AB了。
A
D
E
B
C
你能解释此方案的合理性吗?
测量应用
(变式) 有一条河的两岸某一段是平行的,在该河岸的这一段每隔5米有一棵树,河的对岸每隔50米有一电线杆,在河岸离开岸边25米处看对岸,看到对岸相邻的两根电线杆恰好被河岸的两棵树遮住,且这两棵树之间还有3棵树,求河宽.
[解析] 依据题意画出示意图,人站在A处,D,E为对岸的两电线杆,B,C为这岸的两棵树,且B,C之间还有3棵树,AM为人到这岸的距离,DE=50米,BC=20米,AM⊥BC,且AM=25米.
测量应用
解:如图,由BC∥DE可得△ABC∽△ADE.
[归纳] 本题利用相似三角形的性质解决实际问题,关键是画出图形,建立相似三角形的模型.
测量应用
小结
实际问题转化为数学模型
“转化”思想
应用相似三角形的性质解决实际问题时(如测量问题),
一般分为以下三个步骤:
①审题 ②构建图形 ③利用相似解决问题
作业
课本 P90页:
习题22.3:题 10、11、12、13.
谢 谢
