沪科版数学九年级上册 21.1 二次函数 教案
文档属性
| 名称 | 沪科版数学九年级上册 21.1 二次函数 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 352.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-04 19:39:09 | ||
图片预览



文档简介
教学目标:
1. 掌握二次函数图像和性质
会求二次函数解析式
二次函数的综合运用
教学重难点:
重点:二次函数的图像和性质
难点:二次函数的综合应用
教学方法:讲练结合
教具准备:多媒体
教学过程:
二次函数的定义
1.定义:一般地,形如 y=ax +bx+c(a,b,c是常数,a≠0)的函数叫做二次函数.
2.定义要点:
(1)关于x的代数式一定是整式,a,b,c为常数,且a≠0.
(2)等式的右边最高次数为2,可以没有一次项和常数项,但不能没有二次项.
如: y=-x2, y=2x2-4x+3 , y=100-5x2,y=-2x2+5x-3 等等都是二次函数。
(
解:根据题意,
得
)
由①得,K≠0.5
由②得,K=0.5或-1
所以K=-1
小结
生小结师补充
作业
二次函数专项试卷
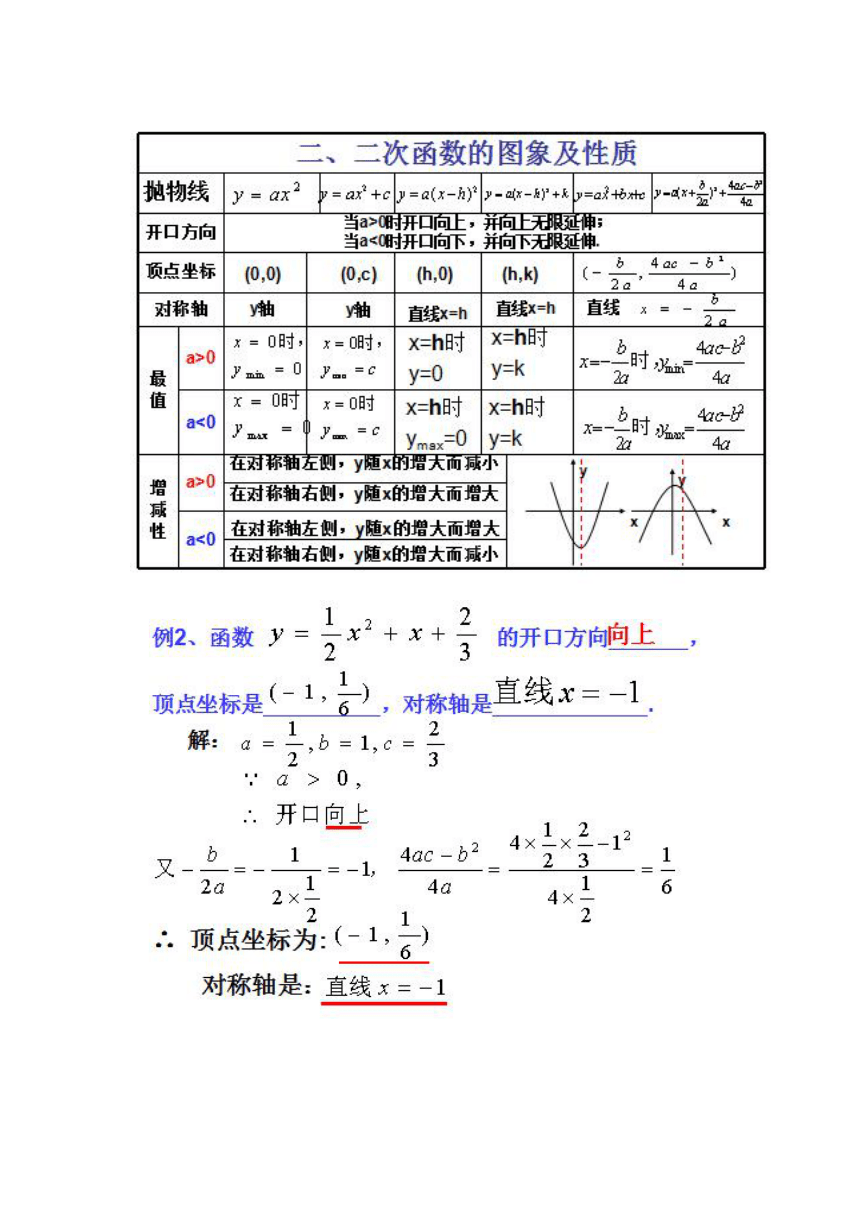
例2、函数
的开口方向向上,
顶点坐标
对称轴
顶点坐标为
对称轴是:直线
的图象和性质
的系数a,b,c与图象的关系
‖定开口力向:a>0时开囗向上,a练习
无论k取什么实数
图象顶点必在
直线
直线y
y
轴
若所求的
数的图象与抛物线
有相同的顶点,并且在对称轴左侧,y随x的增
增大,在对称轴右侧,y随x的增大而减
所求
的二次函数的解析式
3、二次函数
0)的图象如
图所示,则
c的符号为
a>0.b=0
b=0.c
=0.c<
4、二次函数y=a
(a≠
次函数
在同一坐标系内的大致图象是(
练
次函数y=a
(a≠0)的图象如图所示
b、c的符
B、a<0.b>0
函数y=a
a≠0)的图象
如图所示
c的符号为
B
练习
次函数
的图象
如上图所示,那么下列判断正确的有(填
序号)
次函数解析式的几种基本形式
般式
知
点坐标
点式
(配方式)
知顶点坐标、对称轴或最值
练习
根据下列条件选择合适的方法求二次函数解析式
抛物线经过(2
2)(2,3)
2、抛物线的顶点坐标是
2),且与X轴的
交点的横坐标是8
抛物线经过点(4,3),且x=3时y的最大值是4
函数图象上的点的坐标求
求下列条件下的二次函数的解析式
已知
数的图象经过
已知二次函数的图象的顶点坐标为
且图象过点
已知
数的图象与x轴交
和(6,0),并且
经过点
数形结
如图直线经过点A(4,0)和B(0,4)两点,它与
函数y=ax2的图像在第一象限内相交于P点若
△AOP的面积为6、(1)求二次函数的解析式
解;由已知A(4,0,B(,4)得直线AB的解
析式为y=x+4,
时3x+4
在抛物线
把x=1,y=3代入y=ax2,得a
1. 掌握二次函数图像和性质
会求二次函数解析式
二次函数的综合运用
教学重难点:
重点:二次函数的图像和性质
难点:二次函数的综合应用
教学方法:讲练结合
教具准备:多媒体
教学过程:
二次函数的定义
1.定义:一般地,形如 y=ax +bx+c(a,b,c是常数,a≠0)的函数叫做二次函数.
2.定义要点:
(1)关于x的代数式一定是整式,a,b,c为常数,且a≠0.
(2)等式的右边最高次数为2,可以没有一次项和常数项,但不能没有二次项.
如: y=-x2, y=2x2-4x+3 , y=100-5x2,y=-2x2+5x-3 等等都是二次函数。
(
解:根据题意,
得
)
由①得,K≠0.5
由②得,K=0.5或-1
所以K=-1
小结
生小结师补充
作业
二次函数专项试卷
例2、函数
的开口方向向上,
顶点坐标
对称轴
顶点坐标为
对称轴是:直线
的图象和性质
的系数a,b,c与图象的关系
‖定开口力向:a>0时开囗向上,a
无论k取什么实数
图象顶点必在
直线
直线y
y
轴
若所求的
数的图象与抛物线
有相同的顶点,并且在对称轴左侧,y随x的增
增大,在对称轴右侧,y随x的增大而减
所求
的二次函数的解析式
3、二次函数
0)的图象如
图所示,则
c的符号为
a>0.b=0
b=0.c
=0.c<
4、二次函数y=a
(a≠
次函数
在同一坐标系内的大致图象是(
练
次函数y=a
(a≠0)的图象如图所示
b、c的符
B、a<0.b>0
函数y=a
a≠0)的图象
如图所示
c的符号为
B
练习
次函数
的图象
如上图所示,那么下列判断正确的有(填
序号)
次函数解析式的几种基本形式
般式
知
点坐标
点式
(配方式)
知顶点坐标、对称轴或最值
练习
根据下列条件选择合适的方法求二次函数解析式
抛物线经过(2
2)(2,3)
2、抛物线的顶点坐标是
2),且与X轴的
交点的横坐标是8
抛物线经过点(4,3),且x=3时y的最大值是4
函数图象上的点的坐标求
求下列条件下的二次函数的解析式
已知
数的图象经过
已知二次函数的图象的顶点坐标为
且图象过点
已知
数的图象与x轴交
和(6,0),并且
经过点
数形结
如图直线经过点A(4,0)和B(0,4)两点,它与
函数y=ax2的图像在第一象限内相交于P点若
△AOP的面积为6、(1)求二次函数的解析式
解;由已知A(4,0,B(,4)得直线AB的解
析式为y=x+4,
时3x+4
在抛物线
把x=1,y=3代入y=ax2,得a
