沪科版数学九年级上册 23.2 解直角三角形 课件(共14张PPT)
文档属性
| 名称 | 沪科版数学九年级上册 23.2 解直角三角形 课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 315.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-05 00:00:00 | ||
图片预览


文档简介
(共14张PPT)
解直角三角形
复习
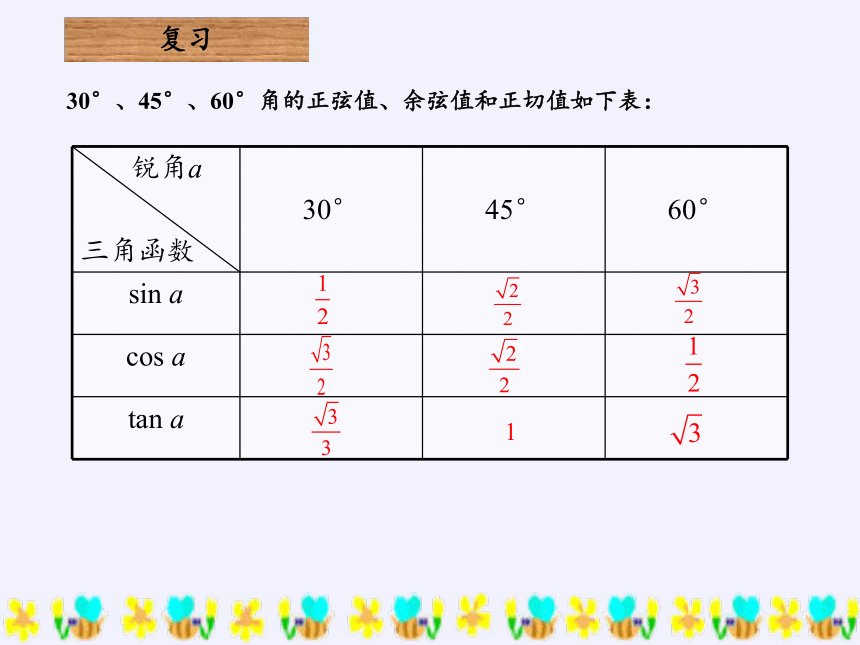
30°、45°、60°角的正弦值、余弦值和正切值如下表:
锐角a 三角函数 30° 45° 60°
sin a
cos a
tan a
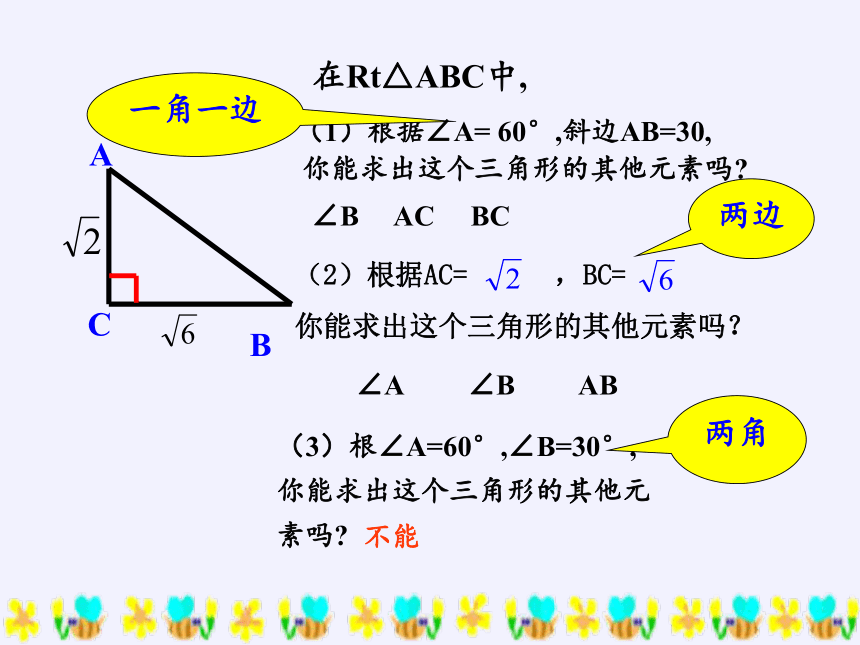
在Rt△ABC中,
(1)根据∠A= 60°,斜边AB=30,
A
B
C
∠B AC BC
∠A ∠B AB
一角一边
两边
(2)根据AC= ,BC=
你能求出这个三角形的其他元素吗?
两角
(3)根∠A=60°,∠B=30°,
你能求出这个三角形的其他元 素吗
不能
你能求出这个三角形的其他元素吗
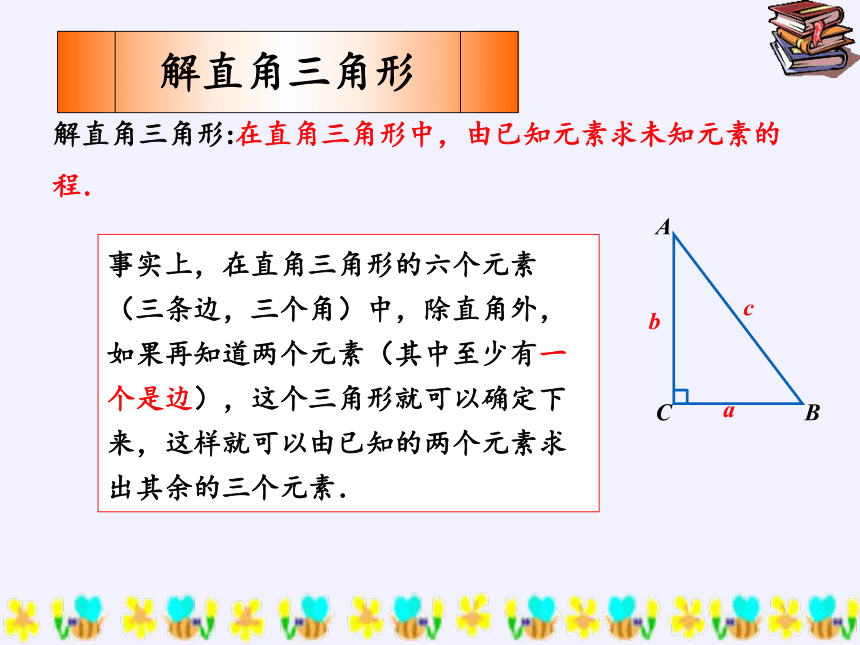
事实上,在直角三角形的六个元素(三条边,三个角)中,除直角外,如果再知道两个元素(其中至少有一个是边),这个三角形就可以确定下来,这样就可以由已知的两个元素求出其余的三个元素.
解直角三角形:在直角三角形中,由已知元素求未知元素的
程.
解直角三角形
A
B
a
b
c
C
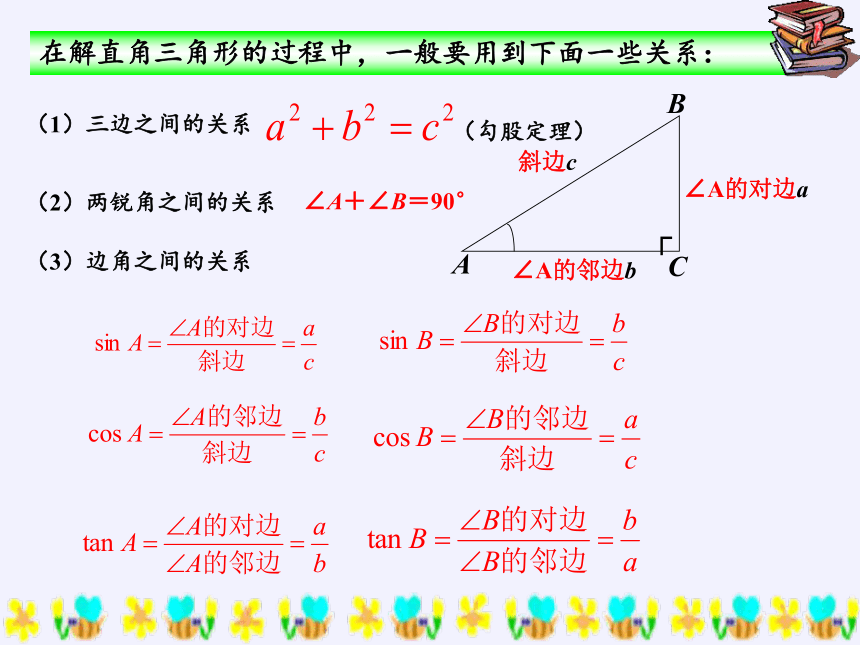
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
(勾股定理)
在解直角三角形的过程中,一般要用到下面一些关系:
A
B
∠A的对边a
C
∠A的邻边b
┌
斜边c
例1、 如图,在Rt△ABC中,∠C=90°,AC=6, ∠BAC的平分线 ,解这个直角三角形ABC.
D
A
B
C
6
解:
因为AD平分∠BAC
典型例题
典型例题3
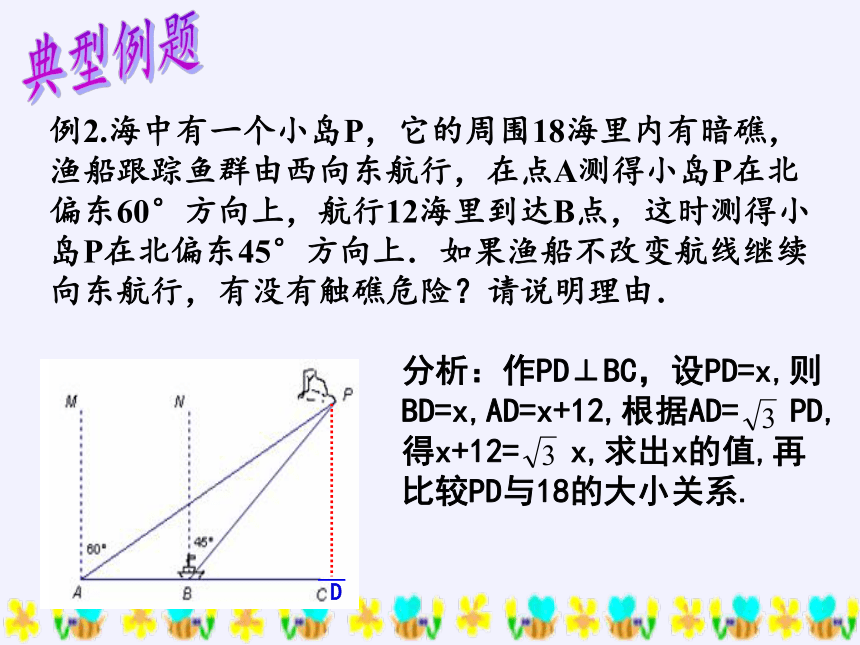
例2.海中有一个小岛P,它的周围18海里内有暗礁,渔船跟踪鱼群由西向东航行,在点A测得小岛P在北偏东60°方向上,航行12海里到达B点,这时测得小岛P在北偏东45°方向上.如果渔船不改变航线继续向东航行,有没有触礁危险?请说明理由.
D
分析:作PD⊥BC,设PD=x,则BD=x,AD=x+12,根据AD= PD,得x+12= x,求出x的值,再比较PD与18的大小关系.
典型例题
D
理由:过点P作PD⊥AC于D.设PD为x,
在Rt△PBD中,∠PBD=90°-45°=45°.
∴BD=PD=x,AD=12+x.
∴渔船不改变航线继续向东航行,有触礁危险.
有触礁危险
解:
在Rt△PAD中,∵∠PAD=90°-60°=30°
A
B
C
m
1.小明为了测量其所在位置,A点到河对岸B点之间的距离,沿着与AB垂直的方向走了m米,到达点C,测得∠ACB=α,那么AB等于( )
(A) m·sinα米 (B) m·tanα米
(C) m·cosα米 (D) 米
B
2. 边长为6cm的等边三角形中,其一边上高的长度为________cm.
【解析】一边上的高=6×sin60°=
巩固练习
3、如图,在等腰直角三角形ABC中,∠C=90°,AC=6,D是
AC上一点,
若tan∠DBA=1/ 5,
求AD的长。
点拨:解三角函数题目最关键的是要构造合适的直角三角形,把已知角放在所构造的直角三角形中。本题已知tan∠DBA= 1/ 5 ,所以可以过点D作DE⊥AB于E,把∠ DBA放于Rt△DBE中,然后根据正切函数的定义,即可弄清DE与BE的长度关系,再结合等腰Rt△的性质,此题就不难解答了。
C
D
A B
E
解:(1)如图,作AD⊥BC于点D,
在Rt△ABD中,AD=AB·sin45°=4× = .
在Rt△ACD中,∵∠ACD=30°
∴AC=2AD= ≈5.6.即新传送带AC的长度约为5.6米.
(2)结论:货物MNQP应挪走.
理由:在Rt△ABD中,BD=AB·cos45°=4× = .
在Rt△ACD中,CD=AC·cos30°= × = .
∴CB=CD-BD= ≈2.1.
∵PC=PB-CB≈4-2.1=1.9<2,
∴货物MNQP应挪走.
解直角
三角形
∠A+ ∠ B=90°
a2+b2=c2
三角函数
关系式
归纳小结
解直角三角形:
由已知元素求未知元素的过程
直角三角形中,
A
B
∠A的对边a
C
∠A的邻边b
┌
斜边c
谢 谢
解直角三角形
复习
30°、45°、60°角的正弦值、余弦值和正切值如下表:
锐角a 三角函数 30° 45° 60°
sin a
cos a
tan a
在Rt△ABC中,
(1)根据∠A= 60°,斜边AB=30,
A
B
C
∠B AC BC
∠A ∠B AB
一角一边
两边
(2)根据AC= ,BC=
你能求出这个三角形的其他元素吗?
两角
(3)根∠A=60°,∠B=30°,
你能求出这个三角形的其他元 素吗
不能
你能求出这个三角形的其他元素吗
事实上,在直角三角形的六个元素(三条边,三个角)中,除直角外,如果再知道两个元素(其中至少有一个是边),这个三角形就可以确定下来,这样就可以由已知的两个元素求出其余的三个元素.
解直角三角形:在直角三角形中,由已知元素求未知元素的
程.
解直角三角形
A
B
a
b
c
C
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
(勾股定理)
在解直角三角形的过程中,一般要用到下面一些关系:
A
B
∠A的对边a
C
∠A的邻边b
┌
斜边c
例1、 如图,在Rt△ABC中,∠C=90°,AC=6, ∠BAC的平分线 ,解这个直角三角形ABC.
D
A
B
C
6
解:
因为AD平分∠BAC
典型例题
典型例题3
例2.海中有一个小岛P,它的周围18海里内有暗礁,渔船跟踪鱼群由西向东航行,在点A测得小岛P在北偏东60°方向上,航行12海里到达B点,这时测得小岛P在北偏东45°方向上.如果渔船不改变航线继续向东航行,有没有触礁危险?请说明理由.
D
分析:作PD⊥BC,设PD=x,则BD=x,AD=x+12,根据AD= PD,得x+12= x,求出x的值,再比较PD与18的大小关系.
典型例题
D
理由:过点P作PD⊥AC于D.设PD为x,
在Rt△PBD中,∠PBD=90°-45°=45°.
∴BD=PD=x,AD=12+x.
∴渔船不改变航线继续向东航行,有触礁危险.
有触礁危险
解:
在Rt△PAD中,∵∠PAD=90°-60°=30°
A
B
C
m
1.小明为了测量其所在位置,A点到河对岸B点之间的距离,沿着与AB垂直的方向走了m米,到达点C,测得∠ACB=α,那么AB等于( )
(A) m·sinα米 (B) m·tanα米
(C) m·cosα米 (D) 米
B
2. 边长为6cm的等边三角形中,其一边上高的长度为________cm.
【解析】一边上的高=6×sin60°=
巩固练习
3、如图,在等腰直角三角形ABC中,∠C=90°,AC=6,D是
AC上一点,
若tan∠DBA=1/ 5,
求AD的长。
点拨:解三角函数题目最关键的是要构造合适的直角三角形,把已知角放在所构造的直角三角形中。本题已知tan∠DBA= 1/ 5 ,所以可以过点D作DE⊥AB于E,把∠ DBA放于Rt△DBE中,然后根据正切函数的定义,即可弄清DE与BE的长度关系,再结合等腰Rt△的性质,此题就不难解答了。
C
D
A B
E
解:(1)如图,作AD⊥BC于点D,
在Rt△ABD中,AD=AB·sin45°=4× = .
在Rt△ACD中,∵∠ACD=30°
∴AC=2AD= ≈5.6.即新传送带AC的长度约为5.6米.
(2)结论:货物MNQP应挪走.
理由:在Rt△ABD中,BD=AB·cos45°=4× = .
在Rt△ACD中,CD=AC·cos30°= × = .
∴CB=CD-BD= ≈2.1.
∵PC=PB-CB≈4-2.1=1.9<2,
∴货物MNQP应挪走.
解直角
三角形
∠A+ ∠ B=90°
a2+b2=c2
三角函数
关系式
归纳小结
解直角三角形:
由已知元素求未知元素的过程
直角三角形中,
A
B
∠A的对边a
C
∠A的邻边b
┌
斜边c
谢 谢
