人教版数学七年级下册 6.2 立方根课件(共25张PPT)
文档属性
| 名称 | 人教版数学七年级下册 6.2 立方根课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-05 00:00:00 | ||
图片预览







文档简介
(共25张PPT)
若一个数的立方等于a,那么这个数叫做 a 的立方根或三次方根。
1、什么是立方根?
2、正数的立方根是一个______,负数的立方根是一个_______,0 的立方根是____;立方根是它本身的数是______.平方根是它本身的数是__算术平方根是它本身的数是______.
正数
负数
0
1、-1、0
0
0、1
回顾
a
1、立方和开立方是互逆运算
平方和开平方是互逆运算
(a≥0)
2.立方根与平方根的异同
相同点: ①0的平方根、立方根都有一个是0
②平方根、立方根都是开方的结果。
不同点:
①定义不同 ②个数不同
③表示方法不同 ④被开方数的取值范围不同
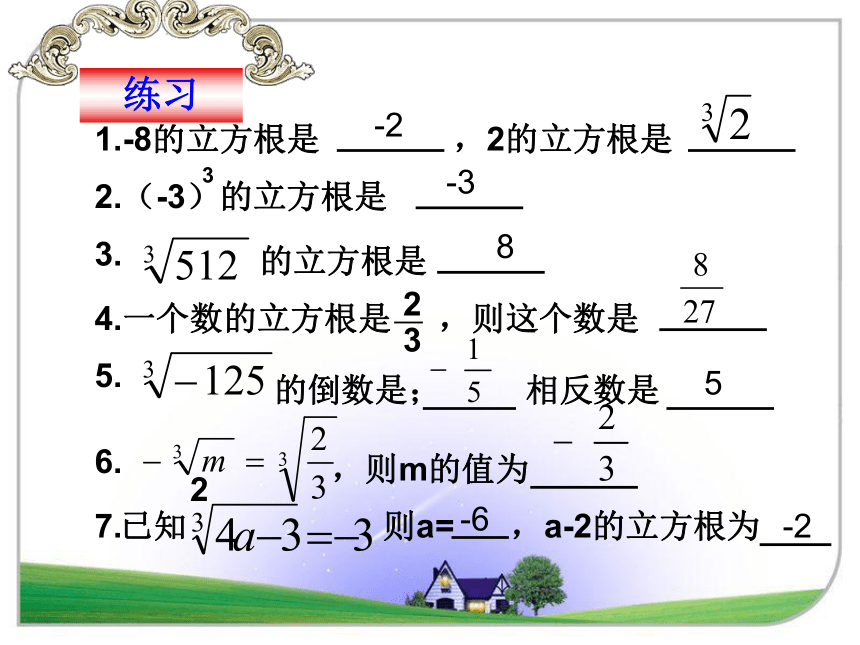
已知 则a= ,a-2的立方根为
1.-8的立方根是
2.(-3)的立方根是
的立方根是
4.一个数的立方根是 ,则这个数是
,2的立方根是
的倒数是; 相反数是
3
3
3.
2
2
5.
,则m的值为
6.
7.
-2
-3
8
5
-6
-2
练习
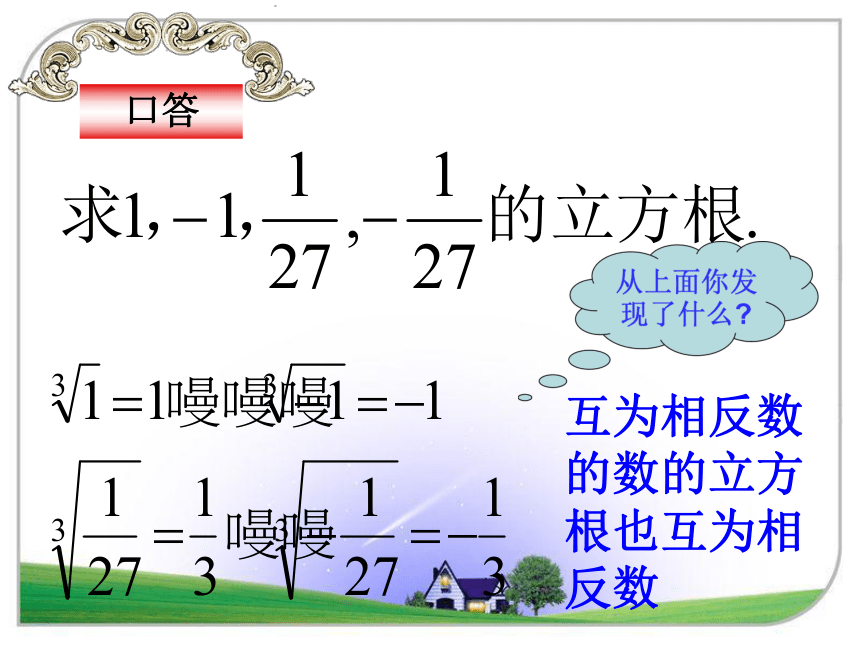
互为相反数的数的立方根也互为相反数
口答
1.求下列数的立方根
2、求下列各式的值
4、求下列各式中x的值
5、当x_________时, 有意义
取任意值
6、将一个立方体的体积扩大到原来的8倍,则它的棱长扩大到原来的_____倍。
2
1.任何有理数都有立方根,它不是正数就
是负数
2.非负数的立方根还是非负数
3.一个数的平方根与其立方根相同,则这
个数是1
不可能是负数
一个数的立方根有两个,它们互为相反
数
6. 27的立方根的平方根是
7.若 ,则
+
x
√
x
x
x
√
√
问题:如果一个立方体的体积是2㎝ ,则这个立方体的棱长是多少呢?
实际上,很多有理数的立方根是无限不循环小数,
,
要求一个数的立方根(或近似值),我们可以利用
键来计算。
如
等都是无限不循环小数。
计算器中的
例1、用计算器求1845的立方根。
依次按键
1845
=
显示:12.264 940 82
练习:用计算器求下列各式的值.
.
0587
.
3
)
6
(
;
5248
.
0
)
5
(
;
69
.
87
4
352
.
0
3
369
.
1
2
09
.
4
1
3
3
3
3
3
3
)
(
;
)
(
;
)
(
;
)
(
例2.用计算器求 的值(计算结果保留4位有效数字).
1.354
=
按 键
显 示
2ndF
0.
1.354
1.106299938
解:用计算器求 的步骤如下:
因为计算结果要求保留4位有效数字,所以
练习:用计算器求下列各数的立方根(保留三位小数)
1728
15625
2197
… …
… …
用计算器计算下列数值,并发现规律
0.06
归纳:被开方数的小数点每向右(或左)移动三位,开方后立方根的小数点就向右(或左)移动一位。
0.6
6
60
观察下面的运算,请你找出其中的规律
规律是:
①被开方数每扩大 倍,其结果就扩大 倍;
②被开方数每缩小 倍,其结果就缩小 倍。
反之也成立。
1
10
0.1
1000
10
1000
10
1.1
110
60
0.6
2
——————。
——————。
——————。
=
=
=
0.06993
-324.6
-0.1507
2280
328000
2、一个正方体的水晶砖,体积为100cm ,
它的棱长大约在 ( )
A、4㎝~5㎝之间
C、6㎝~7㎝之间
B、5cm~6cm之间
D、7㎝~8㎝之间
1、估计68的立方根的大小在( )
A、2与3之间
B、3与4之间
C、4与5之间
D、5与6之间
C
A
3、下列各组数中互为相反数的一组是( )
4、要使 成立,则a必须满足
A
( D )
的整数部分是( ),小数部分是( )
的整数部分是( ),小数部分是( )
6.
7、比较大小
例3:
如图,底面半径为r,高为h的圆柱体的体积
,且圆柱的底面半径与高相等。若
,求这个圆柱的半径
它的体积为2930π
(结果精确到0.1)
h
,
。
解: 由题意,得
答:圆柱的底面半径为14.3
1.354
=
按 键
显 示
2ndF
0.
1.354
1.106299938
解:用计算器求 的步骤如下:
因为计算结果要求保留4位有效数字,所以
若一个数的立方等于a,那么这个数叫做 a 的立方根或三次方根。
1、什么是立方根?
2、正数的立方根是一个______,负数的立方根是一个_______,0 的立方根是____;立方根是它本身的数是______.平方根是它本身的数是__算术平方根是它本身的数是______.
正数
负数
0
1、-1、0
0
0、1
回顾
a
1、立方和开立方是互逆运算
平方和开平方是互逆运算
(a≥0)
2.立方根与平方根的异同
相同点: ①0的平方根、立方根都有一个是0
②平方根、立方根都是开方的结果。
不同点:
①定义不同 ②个数不同
③表示方法不同 ④被开方数的取值范围不同
已知 则a= ,a-2的立方根为
1.-8的立方根是
2.(-3)的立方根是
的立方根是
4.一个数的立方根是 ,则这个数是
,2的立方根是
的倒数是; 相反数是
3
3
3.
2
2
5.
,则m的值为
6.
7.
-2
-3
8
5
-6
-2
练习
互为相反数的数的立方根也互为相反数
口答
1.求下列数的立方根
2、求下列各式的值
4、求下列各式中x的值
5、当x_________时, 有意义
取任意值
6、将一个立方体的体积扩大到原来的8倍,则它的棱长扩大到原来的_____倍。
2
1.任何有理数都有立方根,它不是正数就
是负数
2.非负数的立方根还是非负数
3.一个数的平方根与其立方根相同,则这
个数是1
不可能是负数
一个数的立方根有两个,它们互为相反
数
6. 27的立方根的平方根是
7.若 ,则
+
x
√
x
x
x
√
√
问题:如果一个立方体的体积是2㎝ ,则这个立方体的棱长是多少呢?
实际上,很多有理数的立方根是无限不循环小数,
,
要求一个数的立方根(或近似值),我们可以利用
键来计算。
如
等都是无限不循环小数。
计算器中的
例1、用计算器求1845的立方根。
依次按键
1845
=
显示:12.264 940 82
练习:用计算器求下列各式的值.
.
0587
.
3
)
6
(
;
5248
.
0
)
5
(
;
69
.
87
4
352
.
0
3
369
.
1
2
09
.
4
1
3
3
3
3
3
3
)
(
;
)
(
;
)
(
;
)
(
例2.用计算器求 的值(计算结果保留4位有效数字).
1.354
=
按 键
显 示
2ndF
0.
1.354
1.106299938
解:用计算器求 的步骤如下:
因为计算结果要求保留4位有效数字,所以
练习:用计算器求下列各数的立方根(保留三位小数)
1728
15625
2197
… …
… …
用计算器计算下列数值,并发现规律
0.06
归纳:被开方数的小数点每向右(或左)移动三位,开方后立方根的小数点就向右(或左)移动一位。
0.6
6
60
观察下面的运算,请你找出其中的规律
规律是:
①被开方数每扩大 倍,其结果就扩大 倍;
②被开方数每缩小 倍,其结果就缩小 倍。
反之也成立。
1
10
0.1
1000
10
1000
10
1.1
110
60
0.6
2
——————。
——————。
——————。
=
=
=
0.06993
-324.6
-0.1507
2280
328000
2、一个正方体的水晶砖,体积为100cm ,
它的棱长大约在 ( )
A、4㎝~5㎝之间
C、6㎝~7㎝之间
B、5cm~6cm之间
D、7㎝~8㎝之间
1、估计68的立方根的大小在( )
A、2与3之间
B、3与4之间
C、4与5之间
D、5与6之间
C
A
3、下列各组数中互为相反数的一组是( )
4、要使 成立,则a必须满足
A
( D )
的整数部分是( ),小数部分是( )
的整数部分是( ),小数部分是( )
6.
7、比较大小
例3:
如图,底面半径为r,高为h的圆柱体的体积
,且圆柱的底面半径与高相等。若
,求这个圆柱的半径
它的体积为2930π
(结果精确到0.1)
h
,
。
解: 由题意,得
答:圆柱的底面半径为14.3
1.354
=
按 键
显 示
2ndF
0.
1.354
1.106299938
解:用计算器求 的步骤如下:
因为计算结果要求保留4位有效数字,所以
