2021-2022学年北师大版九年级数学上册《第三章概率的进一步认识》期末综合复习训练 (word版含解析)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学上册《第三章概率的进一步认识》期末综合复习训练 (word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 579.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-05 12:30:41 | ||
图片预览



文档简介
2021-2022学年北师大版九年级数学上册《概率的进一步认识》
期末综合复习训练(附答案)
1.在一个不透明的口袋中装有3个红球和若干个白球,他们除颜色外其他完全相同,通过多次摸球试验后发现,摸到红球的频率稳定在20%附近,则口袋中白球可能有( )
A.6个 B.15个 C.13个 D.12个
2.书架上放着三本古典名著和两本外国小说,小明从中随机抽取两本,两本都是古典名著的概率是( )
A. B. C. D.
3.小红上学要经过两个十字路口,每个路口遇到红、绿灯的机会都相同,小红希望上学时经过每个路口都是绿灯,但实际这样的机会是( )
A. B. C. D.
4.如图电路中,随机闭合开关S1,S2,S3,S4中的两个,能够点亮灯泡的概率为 .
5.投掷一枚质地均匀的骰子两次,向上一面的点数依次记为a,b.那么方程x2+ax+b=0有解的概率是 .
6.如图,有A、B、C三类长方形(或正方形)卡片(a>b),其中甲同学持有A、B类卡片各一张,乙同学持有B、C类卡片各一张,丙同学持有A、C类卡片各一张,现随机选取两位同学手中的卡片共四张进行拼图,则能拼成一个正方形的概率是 .
7.如图,在菱形ABCD四个顶点的字母中,任取两个字母相互交换它们的位置,交换后能使字母A、B在同一条对角线上的概率是 .
8.在一个不透明的袋中装有若干个红球,为了估计袋中红球的个数,小明在袋中放入3个黑球(每个球除颜色外其余都与红球相同),摇匀后每次随机从袋中摸出一个球,记下颜色后放回袋中,通过大量重复摸球试验后发现,摸到红球的频率稳定在0.85左右,则袋中红球约有 个.
9.在试制某种洗发液新品种时,需要选用两种不同的添加剂.现有芳香度分别为0,1,2,3,4,5的六种添加剂可供选用.根据试验设计原理,通常要先从芳香度为0,1,2的三种添加剂中随机选取一种,再从芳香度为3,4,5的三种添加剂中随机选取一种,进行搭配试验,则芳香度之和等于5的概率为 .
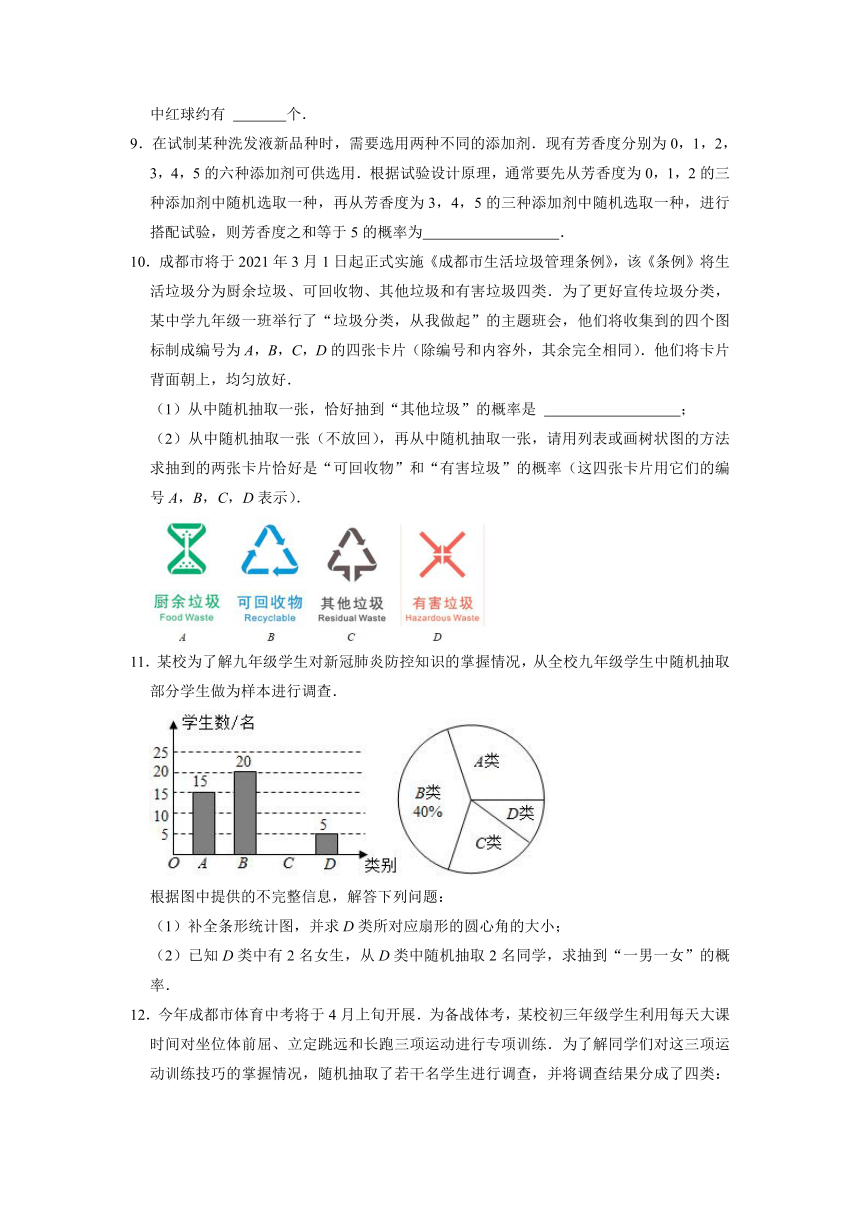
10.成都市将于2021年3月1日起正式实施《成都市生活垃圾管理条例》,该《条例》将生活垃圾分为厨余垃圾、可回收物、其他垃圾和有害垃圾四类.为了更好宣传垃圾分类,某中学九年级一班举行了“垃圾分类,从我做起”的主题班会,他们将收集到的四个图标制成编号为A,B,C,D的四张卡片(除编号和内容外,其余完全相同).他们将卡片背面朝上,均匀放好.
(1)从中随机抽取一张,恰好抽到“其他垃圾”的概率是 ;
(2)从中随机抽取一张(不放回),再从中随机抽取一张,请用列表或画树状图的方法求抽到的两张卡片恰好是“可回收物”和“有害垃圾”的概率(这四张卡片用它们的编号A,B,C,D表示).
11.某校为了解九年级学生对新冠肺炎防控知识的掌握情况,从全校九年级学生中随机抽取部分学生做为样本进行调查.
根据图中提供的不完整信息,解答下列问题:
(1)补全条形统计图,并求D类所对应扇形的圆心角的大小;
(2)已知D类中有2名女生,从D类中随机抽取2名同学,求抽到“一男一女”的概率.
12.今年成都市体育中考将于4月上旬开展.为备战体考,某校初三年级学生利用每天大课时间对坐位体前屈、立定跳远和长跑三项运动进行专项训练.为了解同学们对这三项运动训练技巧的掌握情况,随机抽取了若干名学生进行调查,并将调查结果分成了四类:掌握3项技巧的为A类,掌握2项技巧的为B类,掌握1项技巧的为C类,掌握0项技巧的为D类,并绘制成两幅不完整的统计图.请结合统计图中的信息,解决下列问题:
(1)本次被调查的学生共有 人,请补全条形统计图;
(2)若该校初三年级共有1500名学生,请估计该校初三年级大约有多少名学生掌握了3项训练项目技巧;
(3)D类的4名同学中有且仅有2名来自同一个班,现从D类的4名同学中随机抽取2名同学进行强化训练,请用树状图或表格法求抽到的两个人恰好来自同一个班的概率.
13.最近,学校掀起了志愿服务的热潮,教育处也号召各班学生积极参与,为了解甲、乙两班学生一周服务情况,从这两个班级中各随机抽取40名学生,分别对他们一周的志愿服务时长(单位:分钟)进行收集、整理、分析,给出了部分信息:
a.甲班40名学生一周的志愿服务时长的扇形统计图如图(数据分成6组):
A.20≤x<40,B.40≤x<60,C.60≤x<80,D.80≤x<100,E.100≤x<120,F.120≤x<140);
b.甲班40名学生一周志愿服务时长在60≤x<80这一组的是:
60 60 62 63 65 68 70 72 73 75 75 76 78 78
c.甲、乙两班各抽取的40名学生一周志愿服务时长的平均数、中位数、众数如表:
学校 平均数 中位数 众数
甲 75 m 90
乙 75 76 85
根据以上信息,回答下列问题:
(1)上面图表中的m= ,扇形统计图中“C组”所对应的圆心角的度数为 度;
(2)根据上面的统计结果,你认为 班学生志愿服务工作做得好(填“甲”或“乙”),理由是 ;
(3)小江和小北两位同学都参加了水井坊街道的志愿者服务项目,该街道志愿者服务工作一共设置了三个岗位,请用列表或画树状图的方法,求小江、小北恰好被分配到同一岗位进行志愿者服务的概率.
14.为帮助学生在体育锻炼中享受乐趣、增强体质、健全人格、锤炼意志,某校开展了“一人一球”的体育选修课活动.学生根据自己的喜好选择一门球类项目(A:篮球,B:足球,C:排球,D:羽毛球,E:乒乓球),王老师随机对该校部分学生的选课情况进行调查后;制成了两幅不完整的统计图(如图所示).
(1)王老师调查的学生人数是 ,请将条形统计图补充完整;
(2)若该校共有学生1500名,请估计有多少学生选修乒乓球?
(3)现有4名学生,2人选修篮球,1人选修足球,1人选修排球,王老师要从这4人中任选2人了解他们对体育选修课的看法,请用列表或画树状图的方法,求出所选2人都是选修篮球的概率.
15.我市某中学艺术节期间,向学校学生征集书画作品.九年级美术李老师从全年级14个班中随机抽取了A、B、C、D 4个班,对征集到的作品的数量进行了分析统计,制作了如下两幅不完整的统计图.
(1)李老师采取的调查方式是 (填“普查”或“抽样调查”),李老师所调查的4个班征集到作品共 件,其中B班征集到作品 ,请把图2补充完整.
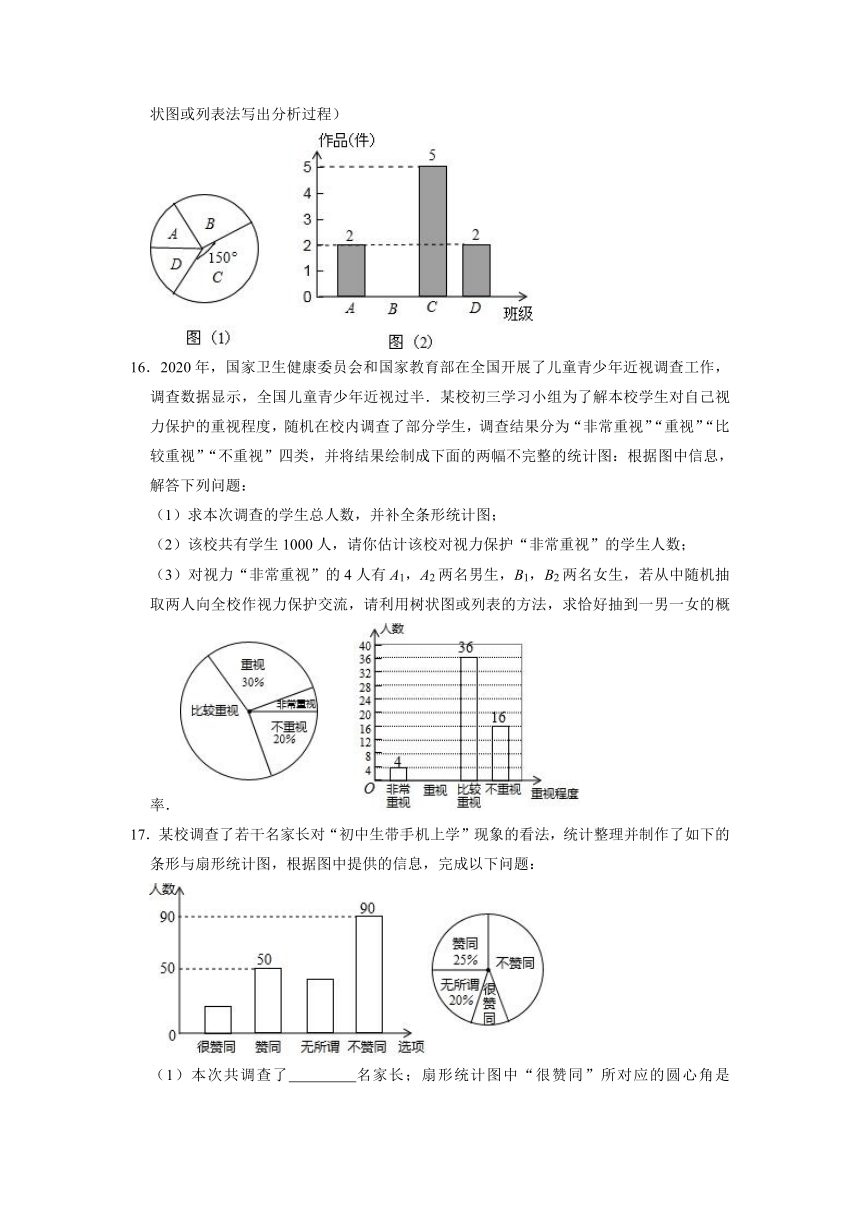
(2)如果全年级参展作品中有4件获得一等奖,其中有2名作者是男生,2名作者是女生.现在要抽两人去参加学校总结表彰座谈会,求恰好抽中一男一女的概率.(要求用树状图或列表法写出分析过程)
16.2020年,国家卫生健康委员会和国家教育部在全国开展了儿童青少年近视调查工作,调查数据显示,全国儿童青少年近视过半.某校初三学习小组为了解本校学生对自己视力保护的重视程度,随机在校内调查了部分学生,调查结果分为“非常重视”“重视”“比较重视”“不重视”四类,并将结果绘制成下面的两幅不完整的统计图:根据图中信息,解答下列问题:
(1)求本次调查的学生总人数,并补全条形统计图;
(2)该校共有学生1000人,请你估计该校对视力保护“非常重视”的学生人数;
(3)对视力“非常重视”的4人有A1,A2两名男生,B1,B2两名女生,若从中随机抽取两人向全校作视力保护交流,请利用树状图或列表的方法,求恰好抽到一男一女的概率.
17.某校调查了若干名家长对“初中生带手机上学”现象的看法,统计整理并制作了如下的条形与扇形统计图,根据图中提供的信息,完成以下问题:
(1)本次共调查了 名家长;扇形统计图中“很赞同”所对应的圆心角是 度.已知该校共有1600名家长,则“不赞同”的家长约有 名;请补全条形统计图;
(2)从“不赞同”的五位家长中(两女三男),随机选取两位家长对全校家长进行“学生使用手机危害性”的专题讲座,请用树状图或列表法求出选中“1男1女”的概率.
18.2019年9月10日是我国第35个教师节,某中学德育处发起了感恩小学恩师的活动,德育处要求每位同学从以下三种方式中选择一种方式表达感恩:A.信件感恩,B.信息感恩,C.当面感恩.为了解同学们选择以上三种感恩方式的情况,德育处随机对本校部分学生进行了调查,并根据调查结果绘制成了如下两幅不完整的统计图.
根据图中信息解答下列问题:
(1)扇形统计图中C部分所对应的扇形圆心角的度数为 ,并补全条形统计图;
(2)本次调查在选择A方式的学生中有两名男生和两名女生来自于同一所小学,德育处打算从他们四个人中选择两位在主题升旗仪式上发言,请用画树状图或列表的方法求恰好选到一男一女的概率.
19.随着经济的快速发展,环境问题越来越受到人们的关注.某校学生会为了了解垃圾分类知识的普及情况,随机调查了部分学生,调查结果分为“非常了解”“了解”“了解较少”“不了解”四类,并将调查结果绘制成下面两幅统计图.
(1)求:本次被调查的学生有多少名?补全条形统计图.
(2)估计该校1200名学生中“非常了解”与“了解”的人数和是多少.
(3)被调查的“非常了解”的学生中有2名男生,其余为女生,从中随机抽取2人在全校做垃圾分类知识交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率.
20.新学期开学初我国中小学生迎来了新版“教育部统编义务教育语文教科书”,本次“统编本”教材最引人关注的变化之一是强调对传统文化经典著作的阅读,某校对A《三国演义》、B《红楼梦》、C《西游记》、D《水浒传》四大名著开展“最受欢迎的传统文化经典著作”调查,随机调查了若干学生(每名学生必选且只能选这四大名著中的一部)并将得到的信息绘制了下面两幅不完整的统计图:
(1)本次一共调查了 名学生;
(2)请将条形统计图补充完整;
(3)某班语文老师想从这四大名著(A、B、C、D)中随机选取两部作为学生暑期必读书籍,请用树状图或列表的方法求恰好选中A和B的概率.
21.一个不透明的口袋里装有分别标有汉字“优”、“教”、“郫”、“都”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀.
(1)若从中任取一个球,球上的汉字刚好是“优”的概率为多少?
(2)从中任取一球,不放回,再从中任取一球,请用树状图或列表的方法,求取出两个球上的汉字能组成“优教”或“郫都”的概率.
参考答案
1.解:设袋中白球的个数为x,
根据题意,得:=20%,
解得x=12,
经检验x=12是分式方程的解,
所以口袋中白球可能有12个,
故选:D.
2.解:用列表法列出所有可能出现的情况如下:
共有20种等可能的情况,其中两本都是古典名著的有6种,
∴P(两本古典名著)==,
故选:C.
3.解:共4种情况,有1种情况每个路口都是绿灯,所以概率为.
故选:A.
4.解:用列表法表示所有可能出现的情况如下:
共有12种可能出现的情况,其中能够点亮灯泡的有8种,
∴P(点亮灯泡)==,
故答案为:.
5.解:画树状图为:
共有36种等可能的结果数,其中使a2﹣4b≥0,即a2≥4b的有19种,
∴方程x2+ax+b=0有解的概率是,
故答案为:.
6.解:由题可得,随机选取两位同学,可能的结果如下:
甲乙、甲丙、乙丙,
∵a2+2ab+b2=(a+b)2,
∴选择乙丙手中的卡片共四张进行拼图,则能拼成一个边长为(a+b)的正方形,
∴能拼成一个正方形的概率为,
故答案为:.
7.解:共有AB互换,AC互换,BC互换,AD互换,CD互换,BD互换6种情况,
符合条件的是BC互换,AD互换2种情况,
所以交换后能使字母A、B在同一条对角线上的概率是=;
故答案为:.
8.解:通过大量重复摸球试验后发现,摸到红球的频率稳定在0.85左右,口袋中有3个黑球,
∵假设有x个红球,
∴=0.85,
解得:x=17,
经检验x=17是分式方程的解,
∴口袋中有红球约有17个.
故答案为:17.
9.解:画树状图为:
共有9种等可能的结果数,其中芳香度之和等于5的结果数为3,
所以芳香度之和等于5的概率=,
故答案为:.
10.解:(1)从中随机抽取一张,恰好抽到“其他垃圾”的概率是,
故答案为:;
(2)画树状图如图:
共有12种等可能的结果,抽到的两张卡片恰好是“可回收物”和“有害垃圾”的结果有2种,
∴抽到的两张卡片恰好是“可回收物”和“有害垃圾”的概率为=.
11.解:抽查的人数为:20×40%=50(人),
∴C类的人数为50﹣15﹣20﹣5=10(人),D类所对应扇形的圆心角的度数为:360°×=36°,
补全条形统计图如下:
(2)画树状图如图:
共有20个等可能的结果,抽到“一男一女”的结果有12个,
∴抽到“一男一女”的概率为=.
12.解:(1)16÷40%=40(人),则C类的人数为:40﹣8﹣16﹣4=12(人),
故答案为:40,
补全条形统计图如下:
(2)1500×=300(名),
即估计该校初三年级大约有300名学生掌握了3项训练项目技巧;
(3)来自同一个班的同学记为A,其他2名同学记为B、C,
画树状图如图:
共有12个等可能的结果,抽到的两个人恰好来自同一个班的结果有2个,
∴抽到的两个人恰好来自同一个班的概率为=.
13.解:(1)由题意得:A的人数为:40×5%=2(人),B的人数为:40×15%=6(人),C的人数为14人,
∴甲班的中位数为=77,
扇形统计图中“C组”所对应的圆心角的度数为:360°×=126°,
故答案为:77,126;
(2)根据上面的统计结果,甲班学生志愿服务工作做得好,理由如下:
①甲、乙两班的平均数相等,甲班的中位数比乙班的中位数大;
②甲班的众数比乙班的众数大;
故答案为:甲,①甲、乙两班的平均数相等,甲班的中位数比乙班的中位数大;②甲班的众数比乙班的众数大;
(3)街道志愿者服务工作一共设置了三个岗位,分别记为A、B、C,画树状图如图:
共有9个等可能的结果,小江、小北恰好被分配到同一岗位进行志愿者服务的结果有3个,
∴小江、小北恰好被分配到同一岗位进行志愿者服务的概率为=.
14.解:(1)该班总人数=10÷20%=50(人).
D人数=50﹣10﹣4﹣16﹣8=12(人),
条形图如图所示:
故答案为:50;补全条形图如图.
(2)1500×=240(人),
答:估计有240学生选修乒乓球.
(3)画树状图为:A:篮球,B:足球,C:排球.
共有12种等可能的结果数,其中所选2人都是选修篮球有2种可能,
所选2人都是选修篮球的概率=.
15.解:(1)∵李老师所调查的4个班征集到作品共:5÷=12(件),
∴B班征集到作品:12﹣2﹣5﹣2=3(件);
∴李老师采取的调查方式是抽样调查,李老师所调查的4个班征集到作品共12件,其中B班征集到作品3件,
故答案为:抽样调查;12;3;
补全图2,如图所示:
(2)画树状图如下:
∵所有等可能的情况有12种,其中一男一女有8种,
∴恰好抽中一男一女的概率为:=.
16.解:(1)本次调查的学生总人数有:16÷20%=80(人);
重视的人数有:80﹣4﹣36﹣16=24(人),补图如下:
(2)根据题意得:
1000×=50(人),
答:该校对视力保护“非常重视”的学生人有50人;
(3)画树状图如下:
共有12种可能的结果,恰好抽到一男一女的结果有8个,
则P(恰好抽到一男一女的)==.
17.解:(1)总人数:50÷25%=200名,无所谓人数:200×20%=40名,很赞同人数:200﹣90﹣50﹣40=20名,
很赞同对应圆心角:360°×=36°,
1600×=720名,
故答案为:200,36,720,补全条形统计图如图所示:
(2)用列表法表示所有可能出现的情况如下:
共有20种可能出现的情况,正确“1男1女”的有12种,
∴P(1男1女)==,
答:选中“1男1女”的概率为.
18.解:(1)被调查的总人数为15÷25%=60(人),C类的总人数=60﹣25﹣15=20(人)
所以扇形统计图中C部分所对应的扇形圆心角的度数为360°×=120°,
补全条形统计图如图所示:
故答案为:120°;
(2)画树状图如下:
共有12种可能的结果,恰好选到一男一女的结果有8个,
∴P(选到一男一女)==.
19.解:(1)本次被调查的学生有由12÷24%=50(人),
则“非常了解”的人数为50×10%=5(人),“了解很少”的人数为50×36%=18(人),
“不了解”的人数为50﹣(5+12+18)=15(人),
补全图形如下:
(2)估计该校1200名学生中“非常了解”与“了解”的人数和是1200×=408(人);
(3)画树状图为:
共有20种等可能的结果数,其中恰好抽到一男一女的有12种结果,
所以恰好抽到一男一女的概率为=.
20.解:(1)本次一共调查:15÷30%=50(人);
故答案为:50;
(2)B对应的人数为:50﹣16﹣15﹣7=12,
如图所示:
(3)列表:
A B C D
A AB AC AD
B BA BC BD
C CA CB CD
D DA DB DC
∵共有12种等可能的结果,恰好选中A、B的有2种,
∴恰好选中A和B的概率为=.
21.解:(1)若从中任取一个球,球上的汉字刚好是“优”的概率为;
(2)列出下表:
优 教 郫 都
优 ﹣﹣ (优,教) (优,郫) (优,都)
教 (教,优) ﹣﹣ (教,郫) (教,都)
郫 (郫,优) (郫,教) ﹣﹣ (郫,都)
都 (都,优) (都,教) (都,郫) ﹣﹣
∴共有12种可能的结果,其中能组成“优教”、“郫都”各有2种可能,
∴按要求能组成“优教”或“郫都”的概率为=.
期末综合复习训练(附答案)
1.在一个不透明的口袋中装有3个红球和若干个白球,他们除颜色外其他完全相同,通过多次摸球试验后发现,摸到红球的频率稳定在20%附近,则口袋中白球可能有( )
A.6个 B.15个 C.13个 D.12个
2.书架上放着三本古典名著和两本外国小说,小明从中随机抽取两本,两本都是古典名著的概率是( )
A. B. C. D.
3.小红上学要经过两个十字路口,每个路口遇到红、绿灯的机会都相同,小红希望上学时经过每个路口都是绿灯,但实际这样的机会是( )
A. B. C. D.
4.如图电路中,随机闭合开关S1,S2,S3,S4中的两个,能够点亮灯泡的概率为 .
5.投掷一枚质地均匀的骰子两次,向上一面的点数依次记为a,b.那么方程x2+ax+b=0有解的概率是 .
6.如图,有A、B、C三类长方形(或正方形)卡片(a>b),其中甲同学持有A、B类卡片各一张,乙同学持有B、C类卡片各一张,丙同学持有A、C类卡片各一张,现随机选取两位同学手中的卡片共四张进行拼图,则能拼成一个正方形的概率是 .
7.如图,在菱形ABCD四个顶点的字母中,任取两个字母相互交换它们的位置,交换后能使字母A、B在同一条对角线上的概率是 .
8.在一个不透明的袋中装有若干个红球,为了估计袋中红球的个数,小明在袋中放入3个黑球(每个球除颜色外其余都与红球相同),摇匀后每次随机从袋中摸出一个球,记下颜色后放回袋中,通过大量重复摸球试验后发现,摸到红球的频率稳定在0.85左右,则袋中红球约有 个.
9.在试制某种洗发液新品种时,需要选用两种不同的添加剂.现有芳香度分别为0,1,2,3,4,5的六种添加剂可供选用.根据试验设计原理,通常要先从芳香度为0,1,2的三种添加剂中随机选取一种,再从芳香度为3,4,5的三种添加剂中随机选取一种,进行搭配试验,则芳香度之和等于5的概率为 .
10.成都市将于2021年3月1日起正式实施《成都市生活垃圾管理条例》,该《条例》将生活垃圾分为厨余垃圾、可回收物、其他垃圾和有害垃圾四类.为了更好宣传垃圾分类,某中学九年级一班举行了“垃圾分类,从我做起”的主题班会,他们将收集到的四个图标制成编号为A,B,C,D的四张卡片(除编号和内容外,其余完全相同).他们将卡片背面朝上,均匀放好.
(1)从中随机抽取一张,恰好抽到“其他垃圾”的概率是 ;
(2)从中随机抽取一张(不放回),再从中随机抽取一张,请用列表或画树状图的方法求抽到的两张卡片恰好是“可回收物”和“有害垃圾”的概率(这四张卡片用它们的编号A,B,C,D表示).
11.某校为了解九年级学生对新冠肺炎防控知识的掌握情况,从全校九年级学生中随机抽取部分学生做为样本进行调查.
根据图中提供的不完整信息,解答下列问题:
(1)补全条形统计图,并求D类所对应扇形的圆心角的大小;
(2)已知D类中有2名女生,从D类中随机抽取2名同学,求抽到“一男一女”的概率.
12.今年成都市体育中考将于4月上旬开展.为备战体考,某校初三年级学生利用每天大课时间对坐位体前屈、立定跳远和长跑三项运动进行专项训练.为了解同学们对这三项运动训练技巧的掌握情况,随机抽取了若干名学生进行调查,并将调查结果分成了四类:掌握3项技巧的为A类,掌握2项技巧的为B类,掌握1项技巧的为C类,掌握0项技巧的为D类,并绘制成两幅不完整的统计图.请结合统计图中的信息,解决下列问题:
(1)本次被调查的学生共有 人,请补全条形统计图;
(2)若该校初三年级共有1500名学生,请估计该校初三年级大约有多少名学生掌握了3项训练项目技巧;
(3)D类的4名同学中有且仅有2名来自同一个班,现从D类的4名同学中随机抽取2名同学进行强化训练,请用树状图或表格法求抽到的两个人恰好来自同一个班的概率.
13.最近,学校掀起了志愿服务的热潮,教育处也号召各班学生积极参与,为了解甲、乙两班学生一周服务情况,从这两个班级中各随机抽取40名学生,分别对他们一周的志愿服务时长(单位:分钟)进行收集、整理、分析,给出了部分信息:
a.甲班40名学生一周的志愿服务时长的扇形统计图如图(数据分成6组):
A.20≤x<40,B.40≤x<60,C.60≤x<80,D.80≤x<100,E.100≤x<120,F.120≤x<140);
b.甲班40名学生一周志愿服务时长在60≤x<80这一组的是:
60 60 62 63 65 68 70 72 73 75 75 76 78 78
c.甲、乙两班各抽取的40名学生一周志愿服务时长的平均数、中位数、众数如表:
学校 平均数 中位数 众数
甲 75 m 90
乙 75 76 85
根据以上信息,回答下列问题:
(1)上面图表中的m= ,扇形统计图中“C组”所对应的圆心角的度数为 度;
(2)根据上面的统计结果,你认为 班学生志愿服务工作做得好(填“甲”或“乙”),理由是 ;
(3)小江和小北两位同学都参加了水井坊街道的志愿者服务项目,该街道志愿者服务工作一共设置了三个岗位,请用列表或画树状图的方法,求小江、小北恰好被分配到同一岗位进行志愿者服务的概率.
14.为帮助学生在体育锻炼中享受乐趣、增强体质、健全人格、锤炼意志,某校开展了“一人一球”的体育选修课活动.学生根据自己的喜好选择一门球类项目(A:篮球,B:足球,C:排球,D:羽毛球,E:乒乓球),王老师随机对该校部分学生的选课情况进行调查后;制成了两幅不完整的统计图(如图所示).
(1)王老师调查的学生人数是 ,请将条形统计图补充完整;
(2)若该校共有学生1500名,请估计有多少学生选修乒乓球?
(3)现有4名学生,2人选修篮球,1人选修足球,1人选修排球,王老师要从这4人中任选2人了解他们对体育选修课的看法,请用列表或画树状图的方法,求出所选2人都是选修篮球的概率.
15.我市某中学艺术节期间,向学校学生征集书画作品.九年级美术李老师从全年级14个班中随机抽取了A、B、C、D 4个班,对征集到的作品的数量进行了分析统计,制作了如下两幅不完整的统计图.
(1)李老师采取的调查方式是 (填“普查”或“抽样调查”),李老师所调查的4个班征集到作品共 件,其中B班征集到作品 ,请把图2补充完整.
(2)如果全年级参展作品中有4件获得一等奖,其中有2名作者是男生,2名作者是女生.现在要抽两人去参加学校总结表彰座谈会,求恰好抽中一男一女的概率.(要求用树状图或列表法写出分析过程)
16.2020年,国家卫生健康委员会和国家教育部在全国开展了儿童青少年近视调查工作,调查数据显示,全国儿童青少年近视过半.某校初三学习小组为了解本校学生对自己视力保护的重视程度,随机在校内调查了部分学生,调查结果分为“非常重视”“重视”“比较重视”“不重视”四类,并将结果绘制成下面的两幅不完整的统计图:根据图中信息,解答下列问题:
(1)求本次调查的学生总人数,并补全条形统计图;
(2)该校共有学生1000人,请你估计该校对视力保护“非常重视”的学生人数;
(3)对视力“非常重视”的4人有A1,A2两名男生,B1,B2两名女生,若从中随机抽取两人向全校作视力保护交流,请利用树状图或列表的方法,求恰好抽到一男一女的概率.
17.某校调查了若干名家长对“初中生带手机上学”现象的看法,统计整理并制作了如下的条形与扇形统计图,根据图中提供的信息,完成以下问题:
(1)本次共调查了 名家长;扇形统计图中“很赞同”所对应的圆心角是 度.已知该校共有1600名家长,则“不赞同”的家长约有 名;请补全条形统计图;
(2)从“不赞同”的五位家长中(两女三男),随机选取两位家长对全校家长进行“学生使用手机危害性”的专题讲座,请用树状图或列表法求出选中“1男1女”的概率.
18.2019年9月10日是我国第35个教师节,某中学德育处发起了感恩小学恩师的活动,德育处要求每位同学从以下三种方式中选择一种方式表达感恩:A.信件感恩,B.信息感恩,C.当面感恩.为了解同学们选择以上三种感恩方式的情况,德育处随机对本校部分学生进行了调查,并根据调查结果绘制成了如下两幅不完整的统计图.
根据图中信息解答下列问题:
(1)扇形统计图中C部分所对应的扇形圆心角的度数为 ,并补全条形统计图;
(2)本次调查在选择A方式的学生中有两名男生和两名女生来自于同一所小学,德育处打算从他们四个人中选择两位在主题升旗仪式上发言,请用画树状图或列表的方法求恰好选到一男一女的概率.
19.随着经济的快速发展,环境问题越来越受到人们的关注.某校学生会为了了解垃圾分类知识的普及情况,随机调查了部分学生,调查结果分为“非常了解”“了解”“了解较少”“不了解”四类,并将调查结果绘制成下面两幅统计图.
(1)求:本次被调查的学生有多少名?补全条形统计图.
(2)估计该校1200名学生中“非常了解”与“了解”的人数和是多少.
(3)被调查的“非常了解”的学生中有2名男生,其余为女生,从中随机抽取2人在全校做垃圾分类知识交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率.
20.新学期开学初我国中小学生迎来了新版“教育部统编义务教育语文教科书”,本次“统编本”教材最引人关注的变化之一是强调对传统文化经典著作的阅读,某校对A《三国演义》、B《红楼梦》、C《西游记》、D《水浒传》四大名著开展“最受欢迎的传统文化经典著作”调查,随机调查了若干学生(每名学生必选且只能选这四大名著中的一部)并将得到的信息绘制了下面两幅不完整的统计图:
(1)本次一共调查了 名学生;
(2)请将条形统计图补充完整;
(3)某班语文老师想从这四大名著(A、B、C、D)中随机选取两部作为学生暑期必读书籍,请用树状图或列表的方法求恰好选中A和B的概率.
21.一个不透明的口袋里装有分别标有汉字“优”、“教”、“郫”、“都”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀.
(1)若从中任取一个球,球上的汉字刚好是“优”的概率为多少?
(2)从中任取一球,不放回,再从中任取一球,请用树状图或列表的方法,求取出两个球上的汉字能组成“优教”或“郫都”的概率.
参考答案
1.解:设袋中白球的个数为x,
根据题意,得:=20%,
解得x=12,
经检验x=12是分式方程的解,
所以口袋中白球可能有12个,
故选:D.
2.解:用列表法列出所有可能出现的情况如下:
共有20种等可能的情况,其中两本都是古典名著的有6种,
∴P(两本古典名著)==,
故选:C.
3.解:共4种情况,有1种情况每个路口都是绿灯,所以概率为.
故选:A.
4.解:用列表法表示所有可能出现的情况如下:
共有12种可能出现的情况,其中能够点亮灯泡的有8种,
∴P(点亮灯泡)==,
故答案为:.
5.解:画树状图为:
共有36种等可能的结果数,其中使a2﹣4b≥0,即a2≥4b的有19种,
∴方程x2+ax+b=0有解的概率是,
故答案为:.
6.解:由题可得,随机选取两位同学,可能的结果如下:
甲乙、甲丙、乙丙,
∵a2+2ab+b2=(a+b)2,
∴选择乙丙手中的卡片共四张进行拼图,则能拼成一个边长为(a+b)的正方形,
∴能拼成一个正方形的概率为,
故答案为:.
7.解:共有AB互换,AC互换,BC互换,AD互换,CD互换,BD互换6种情况,
符合条件的是BC互换,AD互换2种情况,
所以交换后能使字母A、B在同一条对角线上的概率是=;
故答案为:.
8.解:通过大量重复摸球试验后发现,摸到红球的频率稳定在0.85左右,口袋中有3个黑球,
∵假设有x个红球,
∴=0.85,
解得:x=17,
经检验x=17是分式方程的解,
∴口袋中有红球约有17个.
故答案为:17.
9.解:画树状图为:
共有9种等可能的结果数,其中芳香度之和等于5的结果数为3,
所以芳香度之和等于5的概率=,
故答案为:.
10.解:(1)从中随机抽取一张,恰好抽到“其他垃圾”的概率是,
故答案为:;
(2)画树状图如图:
共有12种等可能的结果,抽到的两张卡片恰好是“可回收物”和“有害垃圾”的结果有2种,
∴抽到的两张卡片恰好是“可回收物”和“有害垃圾”的概率为=.
11.解:抽查的人数为:20×40%=50(人),
∴C类的人数为50﹣15﹣20﹣5=10(人),D类所对应扇形的圆心角的度数为:360°×=36°,
补全条形统计图如下:
(2)画树状图如图:
共有20个等可能的结果,抽到“一男一女”的结果有12个,
∴抽到“一男一女”的概率为=.
12.解:(1)16÷40%=40(人),则C类的人数为:40﹣8﹣16﹣4=12(人),
故答案为:40,
补全条形统计图如下:
(2)1500×=300(名),
即估计该校初三年级大约有300名学生掌握了3项训练项目技巧;
(3)来自同一个班的同学记为A,其他2名同学记为B、C,
画树状图如图:
共有12个等可能的结果,抽到的两个人恰好来自同一个班的结果有2个,
∴抽到的两个人恰好来自同一个班的概率为=.
13.解:(1)由题意得:A的人数为:40×5%=2(人),B的人数为:40×15%=6(人),C的人数为14人,
∴甲班的中位数为=77,
扇形统计图中“C组”所对应的圆心角的度数为:360°×=126°,
故答案为:77,126;
(2)根据上面的统计结果,甲班学生志愿服务工作做得好,理由如下:
①甲、乙两班的平均数相等,甲班的中位数比乙班的中位数大;
②甲班的众数比乙班的众数大;
故答案为:甲,①甲、乙两班的平均数相等,甲班的中位数比乙班的中位数大;②甲班的众数比乙班的众数大;
(3)街道志愿者服务工作一共设置了三个岗位,分别记为A、B、C,画树状图如图:
共有9个等可能的结果,小江、小北恰好被分配到同一岗位进行志愿者服务的结果有3个,
∴小江、小北恰好被分配到同一岗位进行志愿者服务的概率为=.
14.解:(1)该班总人数=10÷20%=50(人).
D人数=50﹣10﹣4﹣16﹣8=12(人),
条形图如图所示:
故答案为:50;补全条形图如图.
(2)1500×=240(人),
答:估计有240学生选修乒乓球.
(3)画树状图为:A:篮球,B:足球,C:排球.
共有12种等可能的结果数,其中所选2人都是选修篮球有2种可能,
所选2人都是选修篮球的概率=.
15.解:(1)∵李老师所调查的4个班征集到作品共:5÷=12(件),
∴B班征集到作品:12﹣2﹣5﹣2=3(件);
∴李老师采取的调查方式是抽样调查,李老师所调查的4个班征集到作品共12件,其中B班征集到作品3件,
故答案为:抽样调查;12;3;
补全图2,如图所示:
(2)画树状图如下:
∵所有等可能的情况有12种,其中一男一女有8种,
∴恰好抽中一男一女的概率为:=.
16.解:(1)本次调查的学生总人数有:16÷20%=80(人);
重视的人数有:80﹣4﹣36﹣16=24(人),补图如下:
(2)根据题意得:
1000×=50(人),
答:该校对视力保护“非常重视”的学生人有50人;
(3)画树状图如下:
共有12种可能的结果,恰好抽到一男一女的结果有8个,
则P(恰好抽到一男一女的)==.
17.解:(1)总人数:50÷25%=200名,无所谓人数:200×20%=40名,很赞同人数:200﹣90﹣50﹣40=20名,
很赞同对应圆心角:360°×=36°,
1600×=720名,
故答案为:200,36,720,补全条形统计图如图所示:
(2)用列表法表示所有可能出现的情况如下:
共有20种可能出现的情况,正确“1男1女”的有12种,
∴P(1男1女)==,
答:选中“1男1女”的概率为.
18.解:(1)被调查的总人数为15÷25%=60(人),C类的总人数=60﹣25﹣15=20(人)
所以扇形统计图中C部分所对应的扇形圆心角的度数为360°×=120°,
补全条形统计图如图所示:
故答案为:120°;
(2)画树状图如下:
共有12种可能的结果,恰好选到一男一女的结果有8个,
∴P(选到一男一女)==.
19.解:(1)本次被调查的学生有由12÷24%=50(人),
则“非常了解”的人数为50×10%=5(人),“了解很少”的人数为50×36%=18(人),
“不了解”的人数为50﹣(5+12+18)=15(人),
补全图形如下:
(2)估计该校1200名学生中“非常了解”与“了解”的人数和是1200×=408(人);
(3)画树状图为:
共有20种等可能的结果数,其中恰好抽到一男一女的有12种结果,
所以恰好抽到一男一女的概率为=.
20.解:(1)本次一共调查:15÷30%=50(人);
故答案为:50;
(2)B对应的人数为:50﹣16﹣15﹣7=12,
如图所示:
(3)列表:
A B C D
A AB AC AD
B BA BC BD
C CA CB CD
D DA DB DC
∵共有12种等可能的结果,恰好选中A、B的有2种,
∴恰好选中A和B的概率为=.
21.解:(1)若从中任取一个球,球上的汉字刚好是“优”的概率为;
(2)列出下表:
优 教 郫 都
优 ﹣﹣ (优,教) (优,郫) (优,都)
教 (教,优) ﹣﹣ (教,郫) (教,都)
郫 (郫,优) (郫,教) ﹣﹣ (郫,都)
都 (都,优) (都,教) (都,郫) ﹣﹣
∴共有12种可能的结果,其中能组成“优教”、“郫都”各有2种可能,
∴按要求能组成“优教”或“郫都”的概率为=.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
