2021-2022学年北师大版八年级下册数学3.2图形的旋转课件(共17张PPT)
文档属性
| 名称 | 2021-2022学年北师大版八年级下册数学3.2图形的旋转课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-05 09:54:41 | ||
图片预览






文档简介
(共17张PPT)
3.2 图形的旋转
思考:
以上情景中的转动现象,有什么共同特征?
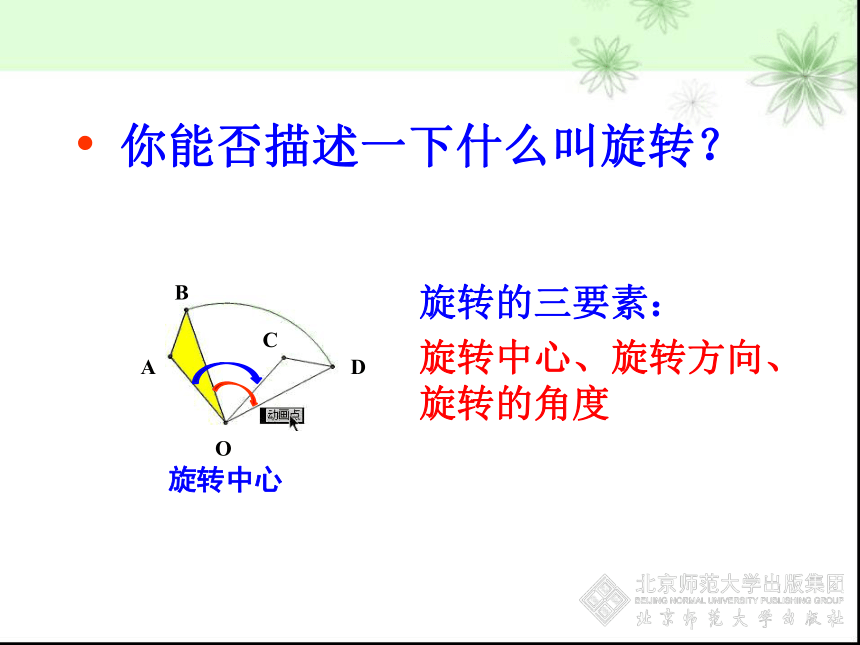
你能否描述一下什么叫旋转?
O
A
B
C
D
旋转的三要素:
旋转中心、旋转方向、旋转的角度
旋转中心
练习
点B的对应点是点_____;线段BC的对应线段是线段______;
线段AB的对应线段是线段______;
∠BAC的对应角是______;
∠ABC的对应角是______;
旋转中心是点______;
旋转的角是 .
(1)如图,△ABC绕点O旋转得到△DEF,则:
O
A
B
C
F
D
E
E
EF
DE
∠EDF
∠DEF
O
∠AOD
或∠BOE
或∠COF
做一做:
1、每小组拿出课前准备的挖有一个图形的硬纸板(三角形、四边形或五边形等),挖一个小洞O作为旋转中心,硬纸板下面放一张白纸。
2、在纸上描出这个挖掉的图形和旋转中心。
3、然后围绕旋转中心转动硬纸板(纸不能动)再描出这个挖掉的图形,移开硬纸板。
1.观察两图形,你发现有哪些相等的线段和相等的角?
2.连接旋转中心和每对对应点,你又能发现有哪些相等的线段和相等的角?
合作探究:
3.在你画的图中,再任取一些对应点,画出它们与旋转中心所连成的线段,你又能发现什么?
4.改变硬纸板上的图形,结论还成立吗?与同伴交流。
例1:如图,正方形ABCD中,E是AD上一点,将△CDE逆时针旋转后得到△CBM.如连接EM,那么△CEM是怎样的三角形
答:由旋转的性质可知∠ECM=∠DCB=90°,(旋转角相等),EC=MC(对应边相等),所以△CEM是等腰直角三角形。
练习1.
如图,(1)~(4)的四个三角形中,哪个不能由△ABC经过平移或旋转得到?
练习2.
如图,四边形ABCD经过旋转后与四边形ADEF重合。
(1)指出这一旋转的旋转中心和旋转角;
(2)写出图中相等的线段和相等的角。
练习3.
如图,你能绕点O旋转,使得线段AB和线段CD重合吗?为什么?
1.这节课学到了什么?
2.你觉得你今天的表现怎么样?
3.你最欣赏谁的表现为什么?
4.你觉得那个小组表现好为什么?
小结:
A类:课本习题3.4第1,2,3题;用学过的有关对称、平移、旋转知识设计一个漂亮的班徽,并要求用简练的语言说明所设计班徽的含义。
B类:课本习题3.4第1,2,4题;在网上收集一些用旋转制作的漂亮图案。
C类:课本习题3.4第1,2题;观察你周围的生活实际,再寻找几个利用旋转的例子
作业
再见,谢谢!
3.2 图形的旋转
思考:
以上情景中的转动现象,有什么共同特征?
你能否描述一下什么叫旋转?
O
A
B
C
D
旋转的三要素:
旋转中心、旋转方向、旋转的角度
旋转中心
练习
点B的对应点是点_____;线段BC的对应线段是线段______;
线段AB的对应线段是线段______;
∠BAC的对应角是______;
∠ABC的对应角是______;
旋转中心是点______;
旋转的角是 .
(1)如图,△ABC绕点O旋转得到△DEF,则:
O
A
B
C
F
D
E
E
EF
DE
∠EDF
∠DEF
O
∠AOD
或∠BOE
或∠COF
做一做:
1、每小组拿出课前准备的挖有一个图形的硬纸板(三角形、四边形或五边形等),挖一个小洞O作为旋转中心,硬纸板下面放一张白纸。
2、在纸上描出这个挖掉的图形和旋转中心。
3、然后围绕旋转中心转动硬纸板(纸不能动)再描出这个挖掉的图形,移开硬纸板。
1.观察两图形,你发现有哪些相等的线段和相等的角?
2.连接旋转中心和每对对应点,你又能发现有哪些相等的线段和相等的角?
合作探究:
3.在你画的图中,再任取一些对应点,画出它们与旋转中心所连成的线段,你又能发现什么?
4.改变硬纸板上的图形,结论还成立吗?与同伴交流。
例1:如图,正方形ABCD中,E是AD上一点,将△CDE逆时针旋转后得到△CBM.如连接EM,那么△CEM是怎样的三角形
答:由旋转的性质可知∠ECM=∠DCB=90°,(旋转角相等),EC=MC(对应边相等),所以△CEM是等腰直角三角形。
练习1.
如图,(1)~(4)的四个三角形中,哪个不能由△ABC经过平移或旋转得到?
练习2.
如图,四边形ABCD经过旋转后与四边形ADEF重合。
(1)指出这一旋转的旋转中心和旋转角;
(2)写出图中相等的线段和相等的角。
练习3.
如图,你能绕点O旋转,使得线段AB和线段CD重合吗?为什么?
1.这节课学到了什么?
2.你觉得你今天的表现怎么样?
3.你最欣赏谁的表现为什么?
4.你觉得那个小组表现好为什么?
小结:
A类:课本习题3.4第1,2,3题;用学过的有关对称、平移、旋转知识设计一个漂亮的班徽,并要求用简练的语言说明所设计班徽的含义。
B类:课本习题3.4第1,2,4题;在网上收集一些用旋转制作的漂亮图案。
C类:课本习题3.4第1,2题;观察你周围的生活实际,再寻找几个利用旋转的例子
作业
再见,谢谢!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
