2021-2022学年高一上学期数学人教A版(2019)必修第一册2.3二次函数与一元二次方程、不等式(第一课时)课件(共20张PPT)
文档属性
| 名称 | 2021-2022学年高一上学期数学人教A版(2019)必修第一册2.3二次函数与一元二次方程、不等式(第一课时)课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 675.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-04 09:19:30 | ||
图片预览






文档简介
(共20张PPT)
第2章 一元二次函数、方程和不等式
2.3 二次函数与一元二 次方程、不等式
(第一课时)
1.经历从实际情境中抽象出一元二次不等式的过程,了解一元二次不等式的现实意义.
2.能借助一元二次函数求解一元二次不等式,并能用集合表示一元二次不等式的解集.
课标要求
素养要求
从函数观点认识不等式,感悟数学知识之间的关联,认识函数的重要性,重点提升数学抽象和数学运算素养.
①已知三个方程:x2-4x+3=0;x2-4x+4=0;x2-4x+5=0.
②已知三个函数y1=x2-4x+3,y2=x2-4x+4,y3=x2-4x+5及三个函数对应的图象.
问题1:①中三个方程的解分别是什么?,
问题2:②中三个函数与x轴交点横坐标分别是什么?
问题3:由图象观察可知在②中三个函数中,x分别取何值时函数值为正、负?
一. 问题引入
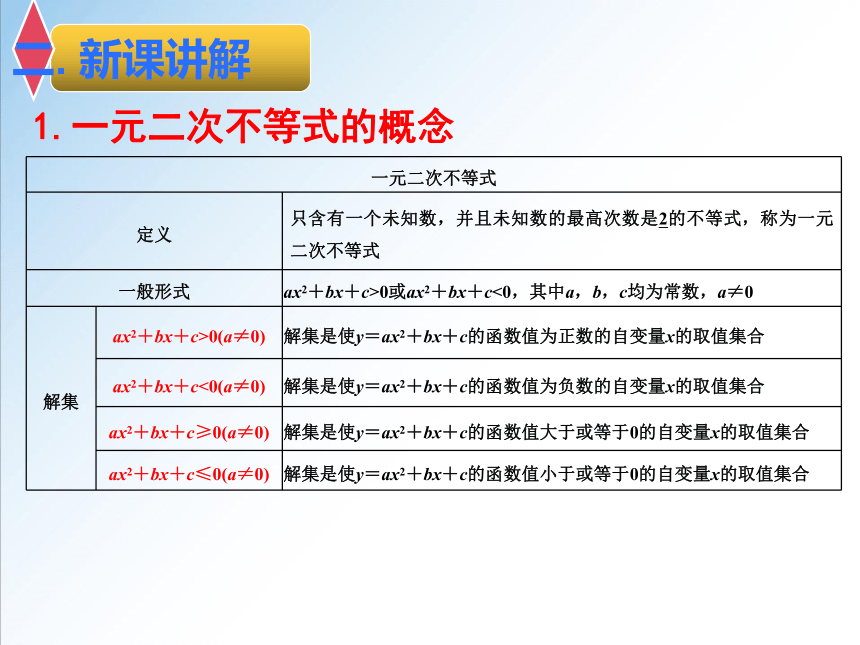
1.一元二次不等式的概念
一元二次不等式 定义 只含有一个未知数,并且未知数的最高次数是2的不等式,称为一元二次不等式
一般形式 ax2+bx+c>0或ax2+bx+c<0,其中a,b,c均为常数,a≠0
解集 ax2+bx+c>0(a≠0) 解集是使y=ax2+bx+c的函数值为正数的自变量x的取值集合
ax2+bx+c<0(a≠0) 解集是使y=ax2+bx+c的函数值为负数的自变量x的取值集合
ax2+bx+c≥0(a≠0) 解集是使y=ax2+bx+c的函数值大于或等于0的自变量x的取值集合
ax2+bx+c≤0(a≠0) 解集是使y=ax2+bx+c的函数值小于或等于0的自变量x的取值集合
二. 新课讲解
方法小结
注意:(1)二次函数的零点不是点,是二次函数与x轴交点的横坐标.
(2)一元二次方程的根是相应一元二次函数的零点.
探究函数、方程、不等式的联系
对于二次函数、一元二次方程和一元二次不等式,
他们的联系又是怎样的呢?
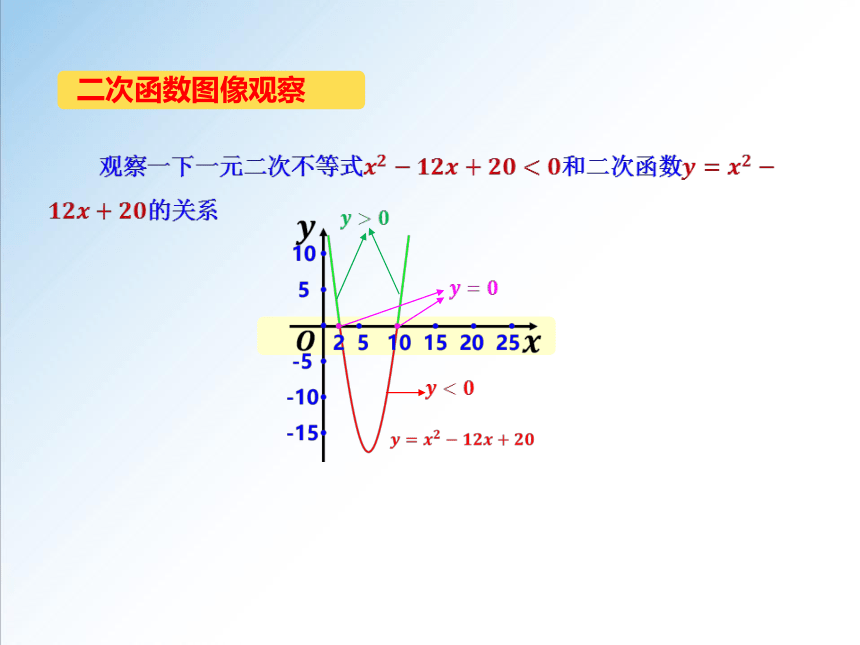
二次函数图像观察
观察一下一元二次不等式和二次函数的关系
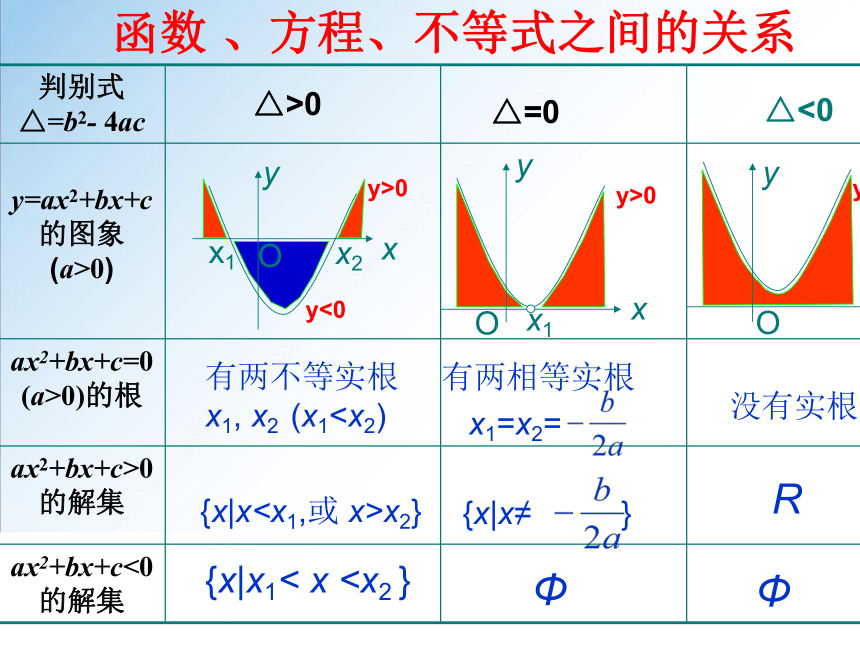
判别式 △=b2- 4ac
y=ax2+bx+c 的图象 (a>0)
ax2+bx+c=0 (a>0)的根
ax2+bx+c>0 的解集
ax2+bx+c<0 的解集
△>0
有两不等实根
x1, x2 (x1{x|xx2}
{x|x1< x△=0
△<0
有两相等实根
x1=x2=
{x|x≠ }
x1
x2
x
y
O
y
x
O
Φ
Φ
R
没有实根
y
x
O
x1
函数 、方程、不等式之间的关系
y>0
y>0
y>0
y<0
注意:
(1)对于一元二次不等式的二次项系数为正且存在两个根的情况下,其解集的常用口诀是:大于取两边,小于取中间.
(2)对于二次项系数是负数(即a<0)的不等式,可以先把二次项系数化为正数,再对照上述情况求解.
例1:解不等式x2-6x-7>0
解:方程x2-6x-7=0的解是
所以,不等式的解集是
{x | x<-1 或 x > 7 }
作函数图象的草图
o
x
y
-1
7
例题分析
例2:解不等式:4x2-4x+1>0
解:∵方程4x2-4x+1=0的判别式
所以,不等式的解集是
作函数图象的草图
o
x
y
0.5
1、 解下列不等式:
(1)2x2+5x-3<0;
(2)-3x2+6x≤2;
(3)4x2-4x+1>0;
(4)-x2+6x-10>0.
课堂练习
2、 解下列不等式:
(1)x2-5x-6>0; (2)(2-x)(x+3)<0;
(1)2x2+5x-3<0;
课堂练习解析
(2)-3x2+6x≤2;
解 原不等式等价于3x2-6x+2≥0.Δ=36-4×3×2=12>0,
把x2的系数化为正数
作出函数y=3x2-6x+2的图象,如图②,
(3)4x2-4x+1>0;
③
(4)-x2+6x-10>0.
解 原不等式可化为x2-6x+10<0,
∵Δ=36-40=-4<0,
∴方程x2-6x+10=0无实根,
∴原不等式的解集为 .
把x2的系数化为正数
(1)x2-5x-6>0; (2)(2-x)(x+3)<0;
2、 解下列不等式:
解 (1)方程x2-5x-6=0的两根为x1=-1,x2=6.
结合二次函数y=x2-5x-6的图象知,原不等式的解集为{x|x<-1或x>6}.
(2)原不等式可化为(x-2)(x+3)>0.
方程(x-2)(x+3)=0的两根为x1=2,x2=-3.
结合二次函数y=(x-2)(x+3)的图象知,原不等式的解集为{x|x<-3或x>2}.
课堂练习解析
解一元二次不等式ax2+bx+c>0 (a≠0)
的步骤:
① 若二次系数为负先将二次系数化为正,然后将二次不等式化成一般式;
② 求出方程ax2+bx+c=0的两根;
④ 根据图象写出不等式的解集.
③ 画出y=ax2+bx+c的图象;
小结
系数化为正,大于取“两端”,小于取“中间”
课后作业
分层训练1-13题
第2章 一元二次函数、方程和不等式
2.3 二次函数与一元二 次方程、不等式
(第一课时)
1.经历从实际情境中抽象出一元二次不等式的过程,了解一元二次不等式的现实意义.
2.能借助一元二次函数求解一元二次不等式,并能用集合表示一元二次不等式的解集.
课标要求
素养要求
从函数观点认识不等式,感悟数学知识之间的关联,认识函数的重要性,重点提升数学抽象和数学运算素养.
①已知三个方程:x2-4x+3=0;x2-4x+4=0;x2-4x+5=0.
②已知三个函数y1=x2-4x+3,y2=x2-4x+4,y3=x2-4x+5及三个函数对应的图象.
问题1:①中三个方程的解分别是什么?,
问题2:②中三个函数与x轴交点横坐标分别是什么?
问题3:由图象观察可知在②中三个函数中,x分别取何值时函数值为正、负?
一. 问题引入
1.一元二次不等式的概念
一元二次不等式 定义 只含有一个未知数,并且未知数的最高次数是2的不等式,称为一元二次不等式
一般形式 ax2+bx+c>0或ax2+bx+c<0,其中a,b,c均为常数,a≠0
解集 ax2+bx+c>0(a≠0) 解集是使y=ax2+bx+c的函数值为正数的自变量x的取值集合
ax2+bx+c<0(a≠0) 解集是使y=ax2+bx+c的函数值为负数的自变量x的取值集合
ax2+bx+c≥0(a≠0) 解集是使y=ax2+bx+c的函数值大于或等于0的自变量x的取值集合
ax2+bx+c≤0(a≠0) 解集是使y=ax2+bx+c的函数值小于或等于0的自变量x的取值集合
二. 新课讲解
方法小结
注意:(1)二次函数的零点不是点,是二次函数与x轴交点的横坐标.
(2)一元二次方程的根是相应一元二次函数的零点.
探究函数、方程、不等式的联系
对于二次函数、一元二次方程和一元二次不等式,
他们的联系又是怎样的呢?
二次函数图像观察
观察一下一元二次不等式和二次函数的关系
判别式 △=b2- 4ac
y=ax2+bx+c 的图象 (a>0)
ax2+bx+c=0 (a>0)的根
ax2+bx+c>0 的解集
ax2+bx+c<0 的解集
△>0
有两不等实根
x1, x2 (x1
{x|x1< x
△<0
有两相等实根
x1=x2=
{x|x≠ }
x1
x2
x
y
O
y
x
O
Φ
Φ
R
没有实根
y
x
O
x1
函数 、方程、不等式之间的关系
y>0
y>0
y>0
y<0
注意:
(1)对于一元二次不等式的二次项系数为正且存在两个根的情况下,其解集的常用口诀是:大于取两边,小于取中间.
(2)对于二次项系数是负数(即a<0)的不等式,可以先把二次项系数化为正数,再对照上述情况求解.
例1:解不等式x2-6x-7>0
解:方程x2-6x-7=0的解是
所以,不等式的解集是
{x | x<-1 或 x > 7 }
作函数图象的草图
o
x
y
-1
7
例题分析
例2:解不等式:4x2-4x+1>0
解:∵方程4x2-4x+1=0的判别式
所以,不等式的解集是
作函数图象的草图
o
x
y
0.5
1、 解下列不等式:
(1)2x2+5x-3<0;
(2)-3x2+6x≤2;
(3)4x2-4x+1>0;
(4)-x2+6x-10>0.
课堂练习
2、 解下列不等式:
(1)x2-5x-6>0; (2)(2-x)(x+3)<0;
(1)2x2+5x-3<0;
课堂练习解析
(2)-3x2+6x≤2;
解 原不等式等价于3x2-6x+2≥0.Δ=36-4×3×2=12>0,
把x2的系数化为正数
作出函数y=3x2-6x+2的图象,如图②,
(3)4x2-4x+1>0;
③
(4)-x2+6x-10>0.
解 原不等式可化为x2-6x+10<0,
∵Δ=36-40=-4<0,
∴方程x2-6x+10=0无实根,
∴原不等式的解集为 .
把x2的系数化为正数
(1)x2-5x-6>0; (2)(2-x)(x+3)<0;
2、 解下列不等式:
解 (1)方程x2-5x-6=0的两根为x1=-1,x2=6.
结合二次函数y=x2-5x-6的图象知,原不等式的解集为{x|x<-1或x>6}.
(2)原不等式可化为(x-2)(x+3)>0.
方程(x-2)(x+3)=0的两根为x1=2,x2=-3.
结合二次函数y=(x-2)(x+3)的图象知,原不等式的解集为{x|x<-3或x>2}.
课堂练习解析
解一元二次不等式ax2+bx+c>0 (a≠0)
的步骤:
① 若二次系数为负先将二次系数化为正,然后将二次不等式化成一般式;
② 求出方程ax2+bx+c=0的两根;
④ 根据图象写出不等式的解集.
③ 画出y=ax2+bx+c的图象;
小结
系数化为正,大于取“两端”,小于取“中间”
课后作业
分层训练1-13题
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
