人教版八上高分笔记之导与练13.3.1.2等腰三角形的判定(原卷+答案)
文档属性
| 名称 | 人教版八上高分笔记之导与练13.3.1.2等腰三角形的判定(原卷+答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-04 10:10:39 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
13.3.1等腰三角形
第2课时 等腰三角形的判定
知识要点:
如果一个三角形有两个角相等,那么这两个角 也相等(简写成 ).
易错点睛:
在ΔABC中,若∠A:∠B:∠C=1:1:2,则ΔABC的形状是_________
【点睛】学生易填直角三角形而出错.
典例讲解:
如图,在ΔABC中,AB=AC,点D,E,F分别在边AB,BC,AC上,且BE=CF,BD=CE.
(1)求证:ΔDEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数.
解题策略:证明两条线段相等,若两条线段在同一个三角形中,可转化为证明两个角相等,再利用等角对等边证明线段相等;若两条线段不在同一个三角形中,可通过证明三角形全等得出线段相等.
变式练习:
如图,在ΔABC中,∠ACB=90°,点D在BC的延长线上,点E在边AB上,DE交AC于点F,AE=EF.求证:ΔDEB为等腰三角形.
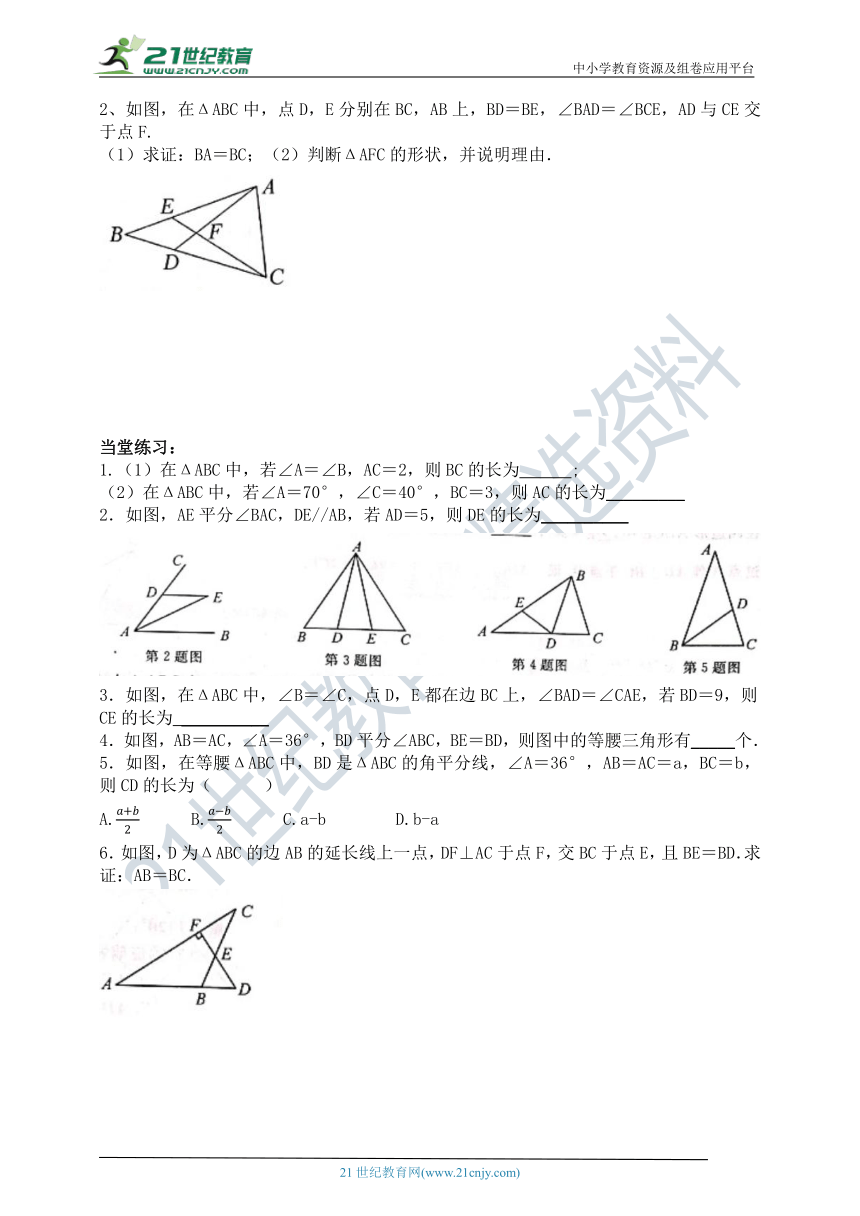
如图,在ΔABC中,点D,E分别在BC,AB上,BD=BE,∠BAD=∠BCE,AD与CE交于点F.
(1)求证:BA=BC;(2)判断ΔAFC的形状,并说明理由.
当堂练习:
1.(1)在ΔABC中,若∠A=∠B,AC=2,则BC的长为 ;
(2)在ΔABC中,若∠A=70°,∠C=40°,BC=3,则AC的长为_________
2.如图,AE平分∠BAC,DE//AB,若AD=5,则DE的长为__________
3.如图,在ΔABC中,∠B=∠C,点D,E都在边BC上,∠BAD=∠CAE,若BD=9,则CE的长为 __________
4.如图,AB=AC,∠A=36°,BD平分∠ABC,BE=BD,则图中的等腰三角形有_____个.
5.如图,在等腰ΔABC中,BD是ΔABC的角平分线,∠A=36°,AB=AC=a,BC=b,则CD的长为( )
A. B. C.a-b D.b-a
6.如图,D为ΔABC的边AB的延长线上一点,DF⊥AC于点F,交BC于点E,且BE=BD.求证:AB=BC.
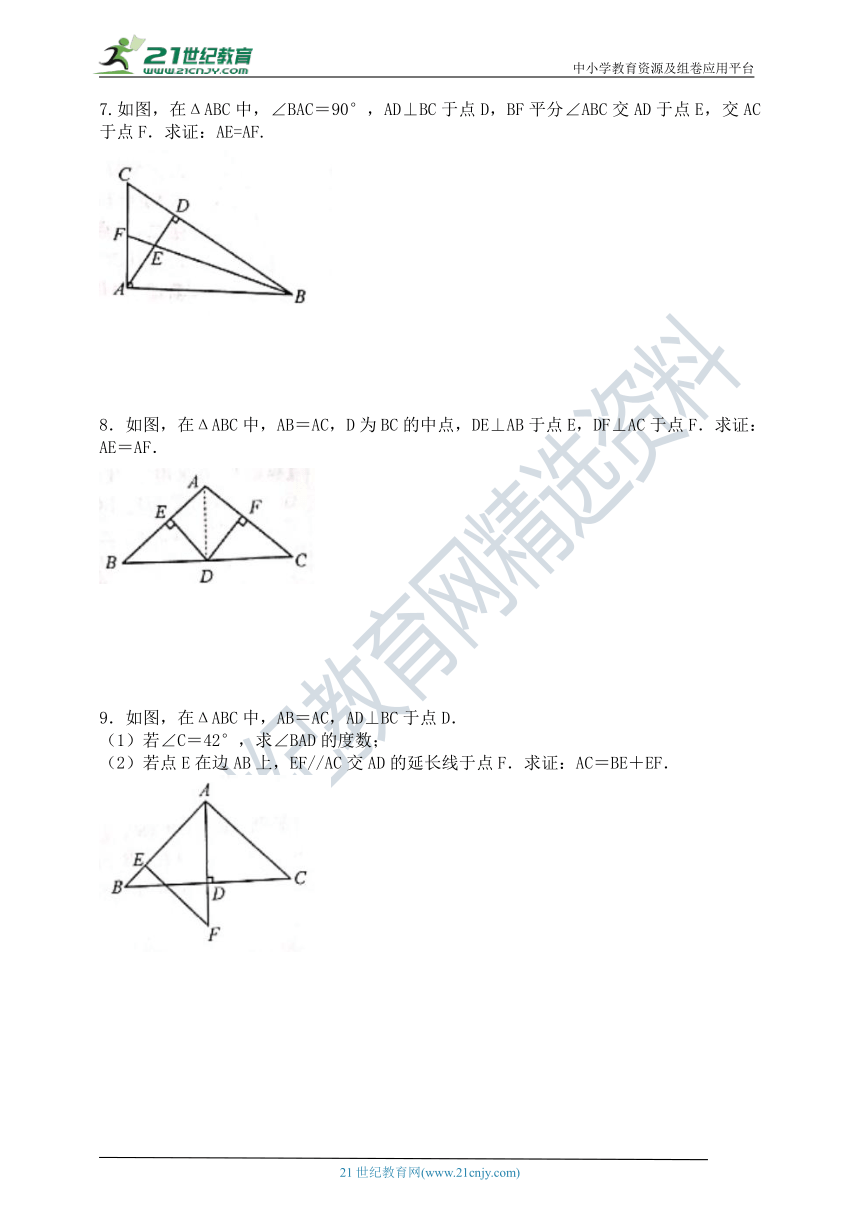
7.如图,在ΔABC中,∠BAC=90°,AD⊥BC于点D,BF平分∠ABC交AD于点E,交AC于点F.求证:AE=AF.
如图,在ΔABC中,AB=AC,D为BC的中点,DE⊥AB于点E,DF⊥AC于点F.求证:AE=AF.
9.如图,在ΔABC中,AB=AC,AD⊥BC于点D.
(1)若∠C=42°,求∠BAD的度数;
(2)若点E在边AB上,EF//AC交AD的延长线于点F.求证:AC=BE+EF.
10.【经典题】如图,在ΔABC中,AB=AC,点D在AB上,点E在AC的延长线上,且BD=CE,DE交BC于点F.求证:DF=EF.
综合题探究
11.如图,在RtΔABC中,∠ACB=90°,AC=BC,D为AB上一点,BD=BC,连接CD,过点C作CE⊥CD,CE=CD,连接DE交CB于点F.
(1)求证:ΔADC≌ΔBDF;
(2)若点O为AB中点,求证:CF=20D.
答案:
知识要点:
如果一个三角形有两个角相等,那么这两个角所对的边 也相等(简写成 等角对等边 ).
易错点睛:
在ΔABC中,若∠A:∠B:∠C=1:1:2,则ΔABC的形状是 等腰直角三角形
【点睛】学生易填直角三角形而出错.
典例讲解:
例1、如图,在ΔABC中,AB=AC,点D,E,F分别在边AB,BC,AC上,且BE=CF,BD=CE.
(1)求证:ΔDEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数.
解:(1)证明:∵AB=AC,∴∠B=∠C.
在ΔDBE和ΔECF中,BE=CF, ∠B=∠C,BD=CE,
∴ΔDBE≌ΔECF(SAS).∴DE=EF.
∴DEF是等腰三角形.
(2)解:如图,由(1)知ΔDBE≌ΔECF,∴∠1=∠2.
∵∠DEC=∠DEF+∠2=∠B+∠1,∴∠DEF=∠B.
∵∠A+∠B+∠C=180°,∠B=∠C,∠A=40°,
∴∠B=70°∴∠DEF=70°
解题策略:证明两条线段相等,若两条线段在同一个三角形中,可转化为证明两个角相等,再利用等角对等边证明线段相等;若两条线段不在同一个三角形中,可通过证明三角形全等得出线段相等.
变式练习:
1、如图,在ΔABC中,∠ACB=90°,点D在BC的延长线上,点E在边AB上,DE交AC于点F,AE=EF.求证:ΔDEB为等腰三角形.
证明:AE=EF,∴∠A=∠AFE.
∵∠AFE=∠DFC,∴∠A=∠DFC.
乂∠ACB=∠FCD=90°,
∴∠A+∠B=90°,∠D+∠DFC=90°.
∴∠D=∠B.
∴DE=BE,即ΔDEB为等腰三角形.
2、如图,在ΔABC中,点D,E分别在BC,AB上,BD=BE,∠BAD=∠BCE,AD与CE交于点F.
(1)求证:BA=BC;(2)判断ΔAFC的形状,并说明理由.
(1)证明:在ΔBAD和ΔBCE中,
∠BAD=∠BCE, ∠B=∠B, BD=BE,
∴ΔBAD≌ΔBCE(AAS)∴BA=BC.
(2)解:ΔAFC是等腰三角形.
理由如下:由(1)知BA=BC,∴∠BAC=∠BCA.
又∠BAD=∠BCE,
∴∠BAC-∠BAD=∠BCA-∠BCE.
∴∠FAC=∠FCA.
∵FA=FC.
∴ΔAFC是等腰三角形.
当堂练习:
1.(1)在ΔABC中,若∠A=∠B,AC=2,则BC的长为 2 ;
(2)在ΔABC中,若∠A=70°,∠C=40°,BC=3,则AC的长为 3
2.如图,AE平分∠BAC,DE//AB,若AD=5,则DE的长为 5
3.如图,在ΔABC中,∠B=∠C,点D,E都在边BC上,∠BAD=∠CAE,若BD=9,则CE的长为 9
4.如图,AB=AC,∠A=36°,BD平分∠ABC,BE=BD,则图中的等腰三角形有5个.
5.如图,在等腰ΔABC中,BD是ΔABC的角平分线,∠A=36°,AB=AC=a,BC=b,则CD的长为( C )
A. B. C.a-b D.b-a
6.如图,D为ΔABC的边AB的延长线上一点,DF⊥AC于点F,交BC于点E,且BE=BD.求证:AB=BC.
证明:证∠C+∠D=90°,∠A+∠D=90°即可.
7.如图,在ΔABC中,∠BAC=90°,AD⊥BC于点D,BF平分∠ABC交AD于点E,交AC于点F.求证:AE=AF.
证明:∵BF平分∠ABC,∴∠ABF=∠CBF.
∵∠BAC=90°∴AD⊥BC,
∴∠ABF+∠AFB=∠CBF+∠BED=90°,
∴∠AFB=∠BED.
∵∠AEF=∠BED,
∴∠AFE=∠AEF,
∴AE=AF.
如图,在ΔABC中,AB=AC,D为BC的中点,DE⊥AB于点E,DF⊥AC于点F.求证:AE=AF.
证明:方法一:证ΔBDE≌ΔCDF;
方法二:连接AD,证AD平分∠BAC,ΔADE≌ΔADF.
9.如图,在ΔABC中,AB=AC,AD⊥BC于点D.
(1)若∠C=42°,求∠BAD的度数;
(2)若点E在边AB上,EF//AC交AD的延长线于点F.求证:AC=BE+EF.
解:(1)∵AB=AC,AD⊥BC于点D,
∴∠BAD=∠CAD,∠ADC=90°,
又∠C=42°,∴∠BAD=∠CAD=90°-42°=48°;
(2)证明:∵AB=AC,AD⊥BC于点D,∴∠BAD=∠CAD,
∵EF//AC,∴∠F=∠CAD,∴∠BAD=∠F,∴AE=FE.
∴AC=AB=AE+BE=EF+BE.
10.【经典题】如图,在ΔABC中,AB=AC,点D在AB上,点E在AC的延长线上,且BD=CE,DE交BC于点F.求证:DF=EF.
证法一:过点D作DM//AC交BC于点M,证ΔDMF≌ΔECF;
证法二:过点E作EN//AB交BC的延长线于点N,证ΔDBF≌ΔENF;
证法三:过点D作DG⊥BC于点G,过点E作EM⊥BC于点M,证ΔBDG≌ΔCEM,ΔDGF≌ΔEMF.
综合题探究
11.如图,在RtΔABC中,∠ACB=90°,AC=BC,D为AB上一点,BD=BC,连接CD,过点C作CE⊥CD,CE=CD,连接DE交CB于点F.
(1)求证:ΔADC≌ΔBDF;
(2)若点O为AB中点,求证:CF=20D.
证明:(1)略;
(2)法一,连接CO,过点D作DH⊥BC,垂足为H,
∵ΔADC≌ΔBFD,∴DC=DF,又 DH⊥BC,∴CF=2CH.易证ΔCDO≌ΔDCH,
∴CH=DO,∴CF=20D;
证法二,连接CO,在OB上截取OM=OD,易证CO⊥AB,
∴CD=CM,∵ΔADC≌ΔBFD,∴BF=AD=BM,又BD=BC,∴CF=DM=2DO.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
13.3.1等腰三角形
第2课时 等腰三角形的判定
知识要点:
如果一个三角形有两个角相等,那么这两个角 也相等(简写成 ).
易错点睛:
在ΔABC中,若∠A:∠B:∠C=1:1:2,则ΔABC的形状是_________
【点睛】学生易填直角三角形而出错.
典例讲解:
如图,在ΔABC中,AB=AC,点D,E,F分别在边AB,BC,AC上,且BE=CF,BD=CE.
(1)求证:ΔDEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数.
解题策略:证明两条线段相等,若两条线段在同一个三角形中,可转化为证明两个角相等,再利用等角对等边证明线段相等;若两条线段不在同一个三角形中,可通过证明三角形全等得出线段相等.
变式练习:
如图,在ΔABC中,∠ACB=90°,点D在BC的延长线上,点E在边AB上,DE交AC于点F,AE=EF.求证:ΔDEB为等腰三角形.
如图,在ΔABC中,点D,E分别在BC,AB上,BD=BE,∠BAD=∠BCE,AD与CE交于点F.
(1)求证:BA=BC;(2)判断ΔAFC的形状,并说明理由.
当堂练习:
1.(1)在ΔABC中,若∠A=∠B,AC=2,则BC的长为 ;
(2)在ΔABC中,若∠A=70°,∠C=40°,BC=3,则AC的长为_________
2.如图,AE平分∠BAC,DE//AB,若AD=5,则DE的长为__________
3.如图,在ΔABC中,∠B=∠C,点D,E都在边BC上,∠BAD=∠CAE,若BD=9,则CE的长为 __________
4.如图,AB=AC,∠A=36°,BD平分∠ABC,BE=BD,则图中的等腰三角形有_____个.
5.如图,在等腰ΔABC中,BD是ΔABC的角平分线,∠A=36°,AB=AC=a,BC=b,则CD的长为( )
A. B. C.a-b D.b-a
6.如图,D为ΔABC的边AB的延长线上一点,DF⊥AC于点F,交BC于点E,且BE=BD.求证:AB=BC.
7.如图,在ΔABC中,∠BAC=90°,AD⊥BC于点D,BF平分∠ABC交AD于点E,交AC于点F.求证:AE=AF.
如图,在ΔABC中,AB=AC,D为BC的中点,DE⊥AB于点E,DF⊥AC于点F.求证:AE=AF.
9.如图,在ΔABC中,AB=AC,AD⊥BC于点D.
(1)若∠C=42°,求∠BAD的度数;
(2)若点E在边AB上,EF//AC交AD的延长线于点F.求证:AC=BE+EF.
10.【经典题】如图,在ΔABC中,AB=AC,点D在AB上,点E在AC的延长线上,且BD=CE,DE交BC于点F.求证:DF=EF.
综合题探究
11.如图,在RtΔABC中,∠ACB=90°,AC=BC,D为AB上一点,BD=BC,连接CD,过点C作CE⊥CD,CE=CD,连接DE交CB于点F.
(1)求证:ΔADC≌ΔBDF;
(2)若点O为AB中点,求证:CF=20D.
答案:
知识要点:
如果一个三角形有两个角相等,那么这两个角所对的边 也相等(简写成 等角对等边 ).
易错点睛:
在ΔABC中,若∠A:∠B:∠C=1:1:2,则ΔABC的形状是 等腰直角三角形
【点睛】学生易填直角三角形而出错.
典例讲解:
例1、如图,在ΔABC中,AB=AC,点D,E,F分别在边AB,BC,AC上,且BE=CF,BD=CE.
(1)求证:ΔDEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数.
解:(1)证明:∵AB=AC,∴∠B=∠C.
在ΔDBE和ΔECF中,BE=CF, ∠B=∠C,BD=CE,
∴ΔDBE≌ΔECF(SAS).∴DE=EF.
∴DEF是等腰三角形.
(2)解:如图,由(1)知ΔDBE≌ΔECF,∴∠1=∠2.
∵∠DEC=∠DEF+∠2=∠B+∠1,∴∠DEF=∠B.
∵∠A+∠B+∠C=180°,∠B=∠C,∠A=40°,
∴∠B=70°∴∠DEF=70°
解题策略:证明两条线段相等,若两条线段在同一个三角形中,可转化为证明两个角相等,再利用等角对等边证明线段相等;若两条线段不在同一个三角形中,可通过证明三角形全等得出线段相等.
变式练习:
1、如图,在ΔABC中,∠ACB=90°,点D在BC的延长线上,点E在边AB上,DE交AC于点F,AE=EF.求证:ΔDEB为等腰三角形.
证明:AE=EF,∴∠A=∠AFE.
∵∠AFE=∠DFC,∴∠A=∠DFC.
乂∠ACB=∠FCD=90°,
∴∠A+∠B=90°,∠D+∠DFC=90°.
∴∠D=∠B.
∴DE=BE,即ΔDEB为等腰三角形.
2、如图,在ΔABC中,点D,E分别在BC,AB上,BD=BE,∠BAD=∠BCE,AD与CE交于点F.
(1)求证:BA=BC;(2)判断ΔAFC的形状,并说明理由.
(1)证明:在ΔBAD和ΔBCE中,
∠BAD=∠BCE, ∠B=∠B, BD=BE,
∴ΔBAD≌ΔBCE(AAS)∴BA=BC.
(2)解:ΔAFC是等腰三角形.
理由如下:由(1)知BA=BC,∴∠BAC=∠BCA.
又∠BAD=∠BCE,
∴∠BAC-∠BAD=∠BCA-∠BCE.
∴∠FAC=∠FCA.
∵FA=FC.
∴ΔAFC是等腰三角形.
当堂练习:
1.(1)在ΔABC中,若∠A=∠B,AC=2,则BC的长为 2 ;
(2)在ΔABC中,若∠A=70°,∠C=40°,BC=3,则AC的长为 3
2.如图,AE平分∠BAC,DE//AB,若AD=5,则DE的长为 5
3.如图,在ΔABC中,∠B=∠C,点D,E都在边BC上,∠BAD=∠CAE,若BD=9,则CE的长为 9
4.如图,AB=AC,∠A=36°,BD平分∠ABC,BE=BD,则图中的等腰三角形有5个.
5.如图,在等腰ΔABC中,BD是ΔABC的角平分线,∠A=36°,AB=AC=a,BC=b,则CD的长为( C )
A. B. C.a-b D.b-a
6.如图,D为ΔABC的边AB的延长线上一点,DF⊥AC于点F,交BC于点E,且BE=BD.求证:AB=BC.
证明:证∠C+∠D=90°,∠A+∠D=90°即可.
7.如图,在ΔABC中,∠BAC=90°,AD⊥BC于点D,BF平分∠ABC交AD于点E,交AC于点F.求证:AE=AF.
证明:∵BF平分∠ABC,∴∠ABF=∠CBF.
∵∠BAC=90°∴AD⊥BC,
∴∠ABF+∠AFB=∠CBF+∠BED=90°,
∴∠AFB=∠BED.
∵∠AEF=∠BED,
∴∠AFE=∠AEF,
∴AE=AF.
如图,在ΔABC中,AB=AC,D为BC的中点,DE⊥AB于点E,DF⊥AC于点F.求证:AE=AF.
证明:方法一:证ΔBDE≌ΔCDF;
方法二:连接AD,证AD平分∠BAC,ΔADE≌ΔADF.
9.如图,在ΔABC中,AB=AC,AD⊥BC于点D.
(1)若∠C=42°,求∠BAD的度数;
(2)若点E在边AB上,EF//AC交AD的延长线于点F.求证:AC=BE+EF.
解:(1)∵AB=AC,AD⊥BC于点D,
∴∠BAD=∠CAD,∠ADC=90°,
又∠C=42°,∴∠BAD=∠CAD=90°-42°=48°;
(2)证明:∵AB=AC,AD⊥BC于点D,∴∠BAD=∠CAD,
∵EF//AC,∴∠F=∠CAD,∴∠BAD=∠F,∴AE=FE.
∴AC=AB=AE+BE=EF+BE.
10.【经典题】如图,在ΔABC中,AB=AC,点D在AB上,点E在AC的延长线上,且BD=CE,DE交BC于点F.求证:DF=EF.
证法一:过点D作DM//AC交BC于点M,证ΔDMF≌ΔECF;
证法二:过点E作EN//AB交BC的延长线于点N,证ΔDBF≌ΔENF;
证法三:过点D作DG⊥BC于点G,过点E作EM⊥BC于点M,证ΔBDG≌ΔCEM,ΔDGF≌ΔEMF.
综合题探究
11.如图,在RtΔABC中,∠ACB=90°,AC=BC,D为AB上一点,BD=BC,连接CD,过点C作CE⊥CD,CE=CD,连接DE交CB于点F.
(1)求证:ΔADC≌ΔBDF;
(2)若点O为AB中点,求证:CF=20D.
证明:(1)略;
(2)法一,连接CO,过点D作DH⊥BC,垂足为H,
∵ΔADC≌ΔBFD,∴DC=DF,又 DH⊥BC,∴CF=2CH.易证ΔCDO≌ΔDCH,
∴CH=DO,∴CF=20D;
证法二,连接CO,在OB上截取OM=OD,易证CO⊥AB,
∴CD=CM,∵ΔADC≌ΔBFD,∴BF=AD=BM,又BD=BC,∴CF=DM=2DO.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
