人教版数学八上高分笔记之导与练13.3.2.1等边三角形的性质和判定(原卷+答案)
文档属性
| 名称 | 人教版数学八上高分笔记之导与练13.3.2.1等边三角形的性质和判定(原卷+答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-04 10:12:12 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
13.3.2等边三角形
等边三角形的性质和判定
知识要点:
等边三角形的性质:(1)等边三角形的三个内角都 ,并且每一个内角都等于 ;(2)等边三角形是 图形,它有 对称轴.
2.等边三角形的判定:(1)三条边都 的三角形是等边三角形;(2)三个角都 的三角形是等边三角形;(3)有一个角是 的等腰三角形是等边三角形.
易错点睛:
如图,等边ΔABC的边长为6,点D为直线BC上一点,BD=2,DE//AB交直线AC于点E,则DE的长为 _________
【点睛】点D可能在点B的右边,也可能在点B的左边.
典例讲解:
题型一、等边三角形性质与判定的应用
例1、如图,等边△ABC中,AD是∠BAC的角平分线,E为AD上一点,以BE为一边且在BE下方作等边△BEF,连接CF.
求证:AE=CF;(2)求∠ACF的度数.
解题策略:题目中出现等边三角形是注意三个性质的应用。
如图,在△MNP中,∠P=60°,MN=NP,MQ⊥PN,垂足为Q,延长MN至点G,使NG=NQ.若△MNP的周长为12,MQ=a,则△MGQ的周长是 ( )
A.8+2a B.8+a C.6+a D.6+2a
2、如图,在四边形ABCD中,AB=AD,AB⊥BC,AD⊥DC,∠BAD=60°,点M,N分别在AB,AD边上,MC=NC.求证:△AMN是等边三角形.
题型二、等边三角形中的动点问题
例2、如图,在△ABC中,AB=BC=AC=12 cm,现有两点M,N分别从点A,B同时出发,沿三角形的边运动.已知点M的速度为1 cm/s,点N的速度为2 cm/s.当点M第一次到达点C时,M,N同时停止运动.
(1)点M,N运动多长时间后,M,N两点恰好重合
(2)点M,N运动多长时间后,△AMN是等边三角形
解题策略:根据题干分类讨论,利用等边建立方程求解。
变式练习:
3、如图1,等边△ABC中,D是AB边上的动点,以CD为一边,向上作等边△EDC,连接AE.
(1)△DBC和△EAC会全等吗?请说说你的理由;
(2)试说明AE∥BC的理由;
(3)如图2,当图1中动点D运动到边BA的延长线上时,所作仍为等边三角形,请问是否仍有AE∥BC?证明你的猜想.
当堂练习:
如图,ΔABC是等边三角形,AD⊥BC于点D,若AB=4,则BD= ,∠BAD=______
2.如图,在ΔABC中,BC的垂直平分线分别交BC,AB于点F,E.若ΔAEC是等边三角形,则∠B= ________
3.如图,P,Q是ΔABC的边BC上的两点,且BP=PQ=QC=AP=AQ,则∠BAC的大小是_________
4.如图,直线a,b分别经过等边三角形ABC的顶点A和C,且a//b,∠1=42°,则∠2的度数为:_____
如图,在等边ΔABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F.
(1)求证:AD=CE;(2)求∠DFC的度数.
6.如图,在一个池塘两旁有一条笔直小路(B,C为小路端点)和一棵小树(A为小树位置).测得的相关数据为:∠ABC=60°,∠ACB=60°,BC=48m,则AC= m.
7.如图,ΔABC是等边三角形,D,E,F分别是AB,BC,CA边上一点,且AD=BE=CF.判断DEF的形状并证明你的结论.
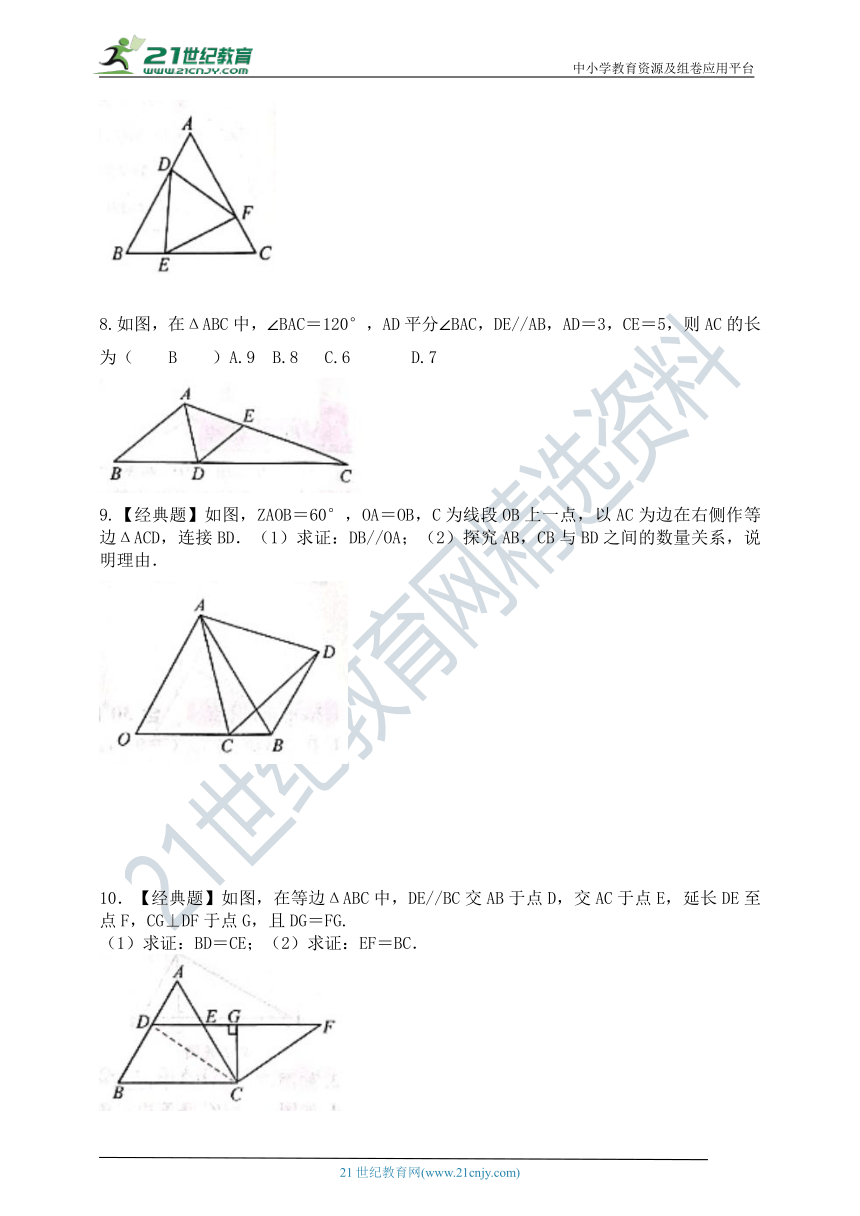
8.如图,在ΔABC中,∠BAC=120°,AD平分∠BAC,DE//AB,AD=3,CE=5,则AC的长为( B )A.9 B.8 C.6 D.7
9.【经典题】如图,ZAOB=60°,OA=OB,C为线段OB上一点,以AC为边在右侧作等边ΔACD,连接BD.(1)求证:DB//OA;(2)探究AB,CB与BD之间的数量关系,说明理由.
10.【经典题】如图,在等边ΔABC中,DE//BC交AB于点D,交AC于点E,延长DE至点F,CG⊥DF于点G,且DG=FG.
(1)求证:BD=CE;(2)求证:EF=BC.
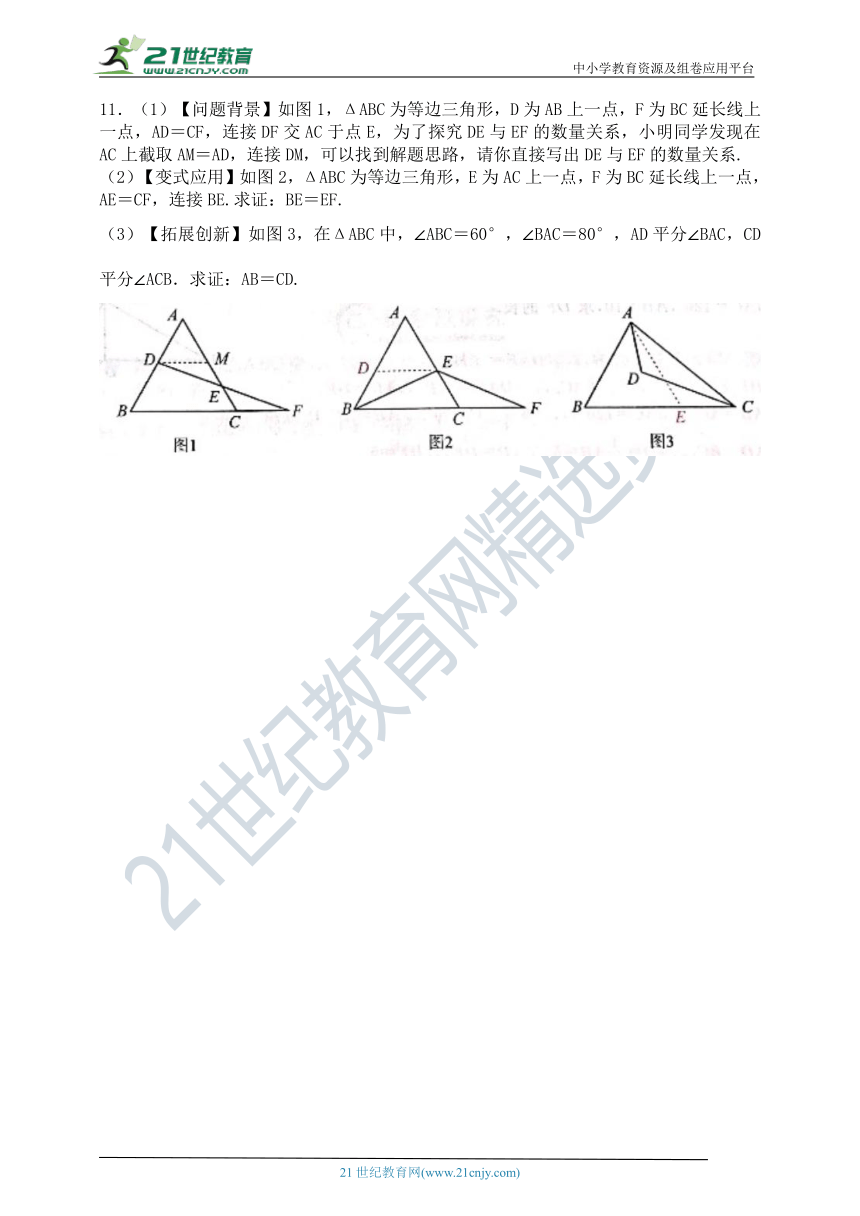
11.(1)【问题背景】如图1,ΔABC为等边三角形,D为AB上一点,F为BC延长线上一点,AD=CF,连接DF交AC于点E,为了探究DE与EF的数量关系,小明同学发现在AC上截取AM=AD,连接DM,可以找到解题思路,请你直接写出DE与EF的数量关系.
(2)【变式应用】如图2,ΔABC为等边三角形,E为AC上一点,F为BC延长线上一点,AE=CF,连接BE.求证:BE=EF.
(3)【拓展创新】如图3,在ΔABC中,∠ABC=60°,∠BAC=80°,AD平分∠BAC,CD平分∠ACB.求证:AB=CD.
答案:
知识要点:
等边三角形的性质:(1)等边三角形的三个内角都 相等,并且每一个内角都等于 60° ;(2)等边三角形是 轴对称 图形,它有 3条对称轴.
2.等边三角形的判定:(1)三条边都 相等 的三角形是等边三角形;(2)三个角都 相等 的三角形是等边三角形;(3)有一个角是 60° 的等腰三角形是等边三角形.
易错点睛:
如图,等边ΔABC的边长为6,点D为直线BC上一点,BD=2,DE//AB交直线AC于点E,则DE的长为4或8
【点睛】点D可能在点B的右边,也可能在点B的左边.
典例讲解:
题型一、等边三角形性质与判定的应用
例1、如图,等边△ABC中,AD是∠BAC的角平分线,E为AD上一点,以BE为一边且在BE下方作等边△BEF,连接CF.
求证:AE=CF;(2)求∠ACF的度数.
解:(1)证明:∵△ABC是等边三角形,∴AB=BC,∠ABE+∠EBC=60°.∵△BEF是等边三角形,
∴EB=BF,∠CBF+∠EBC=60°.∴∠ABE=∠CBF.在△ABE和△CBF中,,
∴△ABE≌△CBF(SAS).∴AE=CF.
(2)∵等边△ABC中,AD是∠BAC的角平分线,∴∠BAE=30°,∠ACB=60°.∵△ABE≌△CBF,∴∠BCF=∠BAE=30°.∴∠ACF=∠BCF+∠ACB=30°+60°=90°.
解题策略:题目中出现等边三角形是注意三个性质的应用。
1、如图,在△MNP中,∠P=60°,MN=NP,MQ⊥PN,垂足为Q,延长MN至点G,使NG=NQ.若△MNP的周长为12,MQ=a,则△MGQ的周长是 ( )D
A.8+2a B.8+a C.6+a D.6+2a
2、如图,在四边形ABCD中,AB=AD,AB⊥BC,AD⊥DC,∠BAD=60°,点M,N分别在AB,AD边上,MC=NC.求证:△AMN是等边三角形.
证明:如图,连接AC.∵AB⊥BC,AD⊥DC,∴∠B=∠D=90°.
在Rt△ABC与Rt△ADC中,
∴Rt△ABC≌Rt△ADC(HL).∴BC=DC.
在Rt△MBC与Rt△NDC中,
∴Rt△MBC≌Rt△NDC(HL).∴BM=DN.
∵AB=AD,∴AM=AN.
又∵∠BAD=60°,∴△AMN是等边三角形.
题型二、等边三角形中的动点问题
例2、如图,在△ABC中,AB=BC=AC=12 cm,现有两点M,N分别从点A,B同时出发,沿三角形的边运动.已知点M的速度为1 cm/s,点N的速度为2 cm/s.当点M第一次到达点C时,M,N同时停止运动.
(1)点M,N运动多长时间后,M,N两点恰好重合
(2)点M,N运动多长时间后,△AMN是等边三角形
解:(1)设点M,N运动x s后,M,N两点恰好重合.由题意,得x×1+12=2x,解得x=12.
∴点M,N运动12 s后,M,N两点恰好重合.
(2)设点M,N运动t s后,△AMN是等边三角形,如图.由题意,得AM=t×1=t(cm),AN=AB-BN=(12-2t)cm.∵△AMN是等边三角形,∴t=12-2t,解得t=4.
∴点M,N运动4 s后,△AMN是等边三角形.
解题策略:根据题干分类讨论,利用等边建立方程求解。
变式练习:
3、如图1,等边△ABC中,D是AB边上的动点,以CD为一边,向上作等边△EDC,连接AE.
(1)△DBC和△EAC会全等吗?请说说你的理由;
(2)试说明AE∥BC的理由;
(3)如图2,当图1中动点D运动到边BA的延长线上时,所作仍为等边三角形,请问是否仍有AE∥BC?证明你的猜想.
解:(1)△DBC和△EAC全等.
理由:∵∠ACB=60°,∠DCE=60°,∴∠BCD=60°-∠ACD,∠ACE=60°-∠ACD,即∠BCD=∠ACE.在△DBC和△EAC中,,∴△DBC≌△EAC(SAS).
∵△DBC≌△EAC,∴∠EAC=∠B=60°.又∵∠ACB=60°,∴∠EAC=∠ACB.∴AE∥BC.(3)结论:AE∥BC.理由:∵△ABC、△EDC为等边三角形,∴BC=AC,DC=CE,∠BCA=∠DCE=60.∴∠BCA+∠ACD=∠DCE+∠ACD,即∠BCD=∠ACE.
在△DBC和△EAC中,,∴△DBC≌△EAC(SAS).∴∠EAC=∠B=60°.又∵∠ACB=60°,∴∠EAC=∠ACB.∴AE∥BC.
当堂练习:
如图,ΔABC是等边三角形,AD⊥BC于点D,若AB=4,则BD= 2,∠BAD= 30°
2.如图,在ΔABC中,BC的垂直平分线分别交BC,AB于点F,E.若ΔAEC是等边三角形,则∠B=30°
3.如图,P,Q是ΔABC的边BC上的两点,且BP=PQ=QC=AP=AQ,则∠BAC的大小是_120°
4.如图,直线a,b分别经过等边三角形ABC的顶点A和C,且a//b,∠1=42°,则∠2的度数为:_____1020
如图,在等边ΔABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F.
(1)求证:AD=CE;(2)求∠DFC的度数.
解:(1)证明略;
(2)∠DFC=60°.
如图,在一个池塘两旁有一条笔直小路(B,C为小路端点)和一棵小树(A为小树位置).测得的相关数据为:∠ABC=60°,∠ACB=60°,BC=48m,则AC=48m.
如图,ΔABC是等边三角形,D,E,F分别是AB,BC,CA边上一点,且AD=BE=CF.判断DEF的形状并证明你的结论.
解:ΔDEF是等边三角形.
∵ΔABC为等边三角形,且AD=BE,
∴AF=BD,∠A=∠B=60°,
∴ΔADF≌ΔBED(SAS).
同理证得ΔADF≌ΔCFE(SAS),
∴ΔADF≌ΔBED≌ΔCFE(SAS),∴DF=ED=EF,:∴ΔDEF是等边三角形.
如图,在ΔABC中,∠BAC=120°,AD平分∠BAC,DE//AB,AD=3,CE=5,则AC的长为( B )A.9 B.8 C.6 D.7
【经典题】如图,ZAOB=60°,OA=OB,C为线段OB上一点,以AC为边在右侧作等边ΔACD,连接BD.(1)求证:DB//OA;(2)探究AB,CB与BD之间的数量关系,说明理由.
证明:(1)易证ΔAOB为等边三角形,∴AB=OA,∠OAB=60°,易证ΔAOC≌ΔABD,
∴∠ABD=∠AOB=60°=∠OAB,
∴BD//OA;
(2)CB+BD=AB,理由如下:ΔAOC≌ΔABD,∴BD=OC,∴CB+BD=CB+OC=OB=AB.
10.【经典题】如图,在等边ΔABC中,DE//BC交AB于点D,交AC于点E,延长DE至点F,CG⊥DF于点G,且DG=FG.
(1)求证:BD=CE;(2)求证:EF=BC.
证明:(1)易证ΔADE是等边三角形,∴AD=AE,∵AB=AC,∴BD=CE;
(2)连接CD,∵CG⊥DF,DG=FG,∴CF=CD,
设∠F=∠CDF=x,
则∠BDC=180°-∠ADC
=180°-(60°+x)=120°-x,
∠ECF=∠ECG+∠GCF=30°+(90°-x)=120°-x,
∴∠BDC=∠ECF,:.ΔBDC≌ΔECF,∴EF=BC.
11.(1)【问题背景】如图1,ΔABC为等边三角形,D为AB上一点,F为BC延长线上一点,AD=CF,连接DF交AC于点E,为了探究DE与EF的数量关系,小明同学发现在AC上截取AM=AD,连接DM,可以找到解题思路,请你直接写出DE与EF的数量关系.
(2)【变式应用】如图2,ΔABC为等边三角形,E为AC上一点,F为BC延长线上一点,AE=CF,连接BE.求证:BE=EF.
(3)【拓展创新】如图3,在ΔABC中,∠ABC=60°,∠BAC=80°,AD平分∠BAC,CD平分∠ACB.求证:AB=CD.
解:(1)DE=EF;
(2)在AB上截取AD=AE,连接DE.
∵ΔABC为等边三角形,
∴∠ACB=∠A=60°,AB=AC.
∵AD=AE,∴ΔADE为等边三角形.∴DE=AD=AE,∠ADE=60°
∵AE=CF,AB=AC,∠ACB=60°,
∴DE=CF,BD=CE,∠BDE=∠ECF=120°
∴ΔBDE≌ΔECF,∴BE=EF;
(3)证明:在BC上截取BE=AB,连接AE.∵∠ABC=60°,
∴ΔABE为等边三角形.
∴AB=AE,∠BAE=60°.∵∠ABC=60°,∠BAC=80°,∴∠EAC=∠BAC-∠BAE=20°,∠ACB=40°. :∵AD平分∠BAC,CD平分∠ACB,.
∴∠BAD=∠CAD=40°,∠ACD=∠BCD=20°.
∴∠DAC=∠ACB=40°,∠ACD=∠EAC=20°.
∵AC=CA,∴ΔACD≌ΔCAE, ∴CD=AE.∵AE=AB,∴AB=CD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
13.3.2等边三角形
等边三角形的性质和判定
知识要点:
等边三角形的性质:(1)等边三角形的三个内角都 ,并且每一个内角都等于 ;(2)等边三角形是 图形,它有 对称轴.
2.等边三角形的判定:(1)三条边都 的三角形是等边三角形;(2)三个角都 的三角形是等边三角形;(3)有一个角是 的等腰三角形是等边三角形.
易错点睛:
如图,等边ΔABC的边长为6,点D为直线BC上一点,BD=2,DE//AB交直线AC于点E,则DE的长为 _________
【点睛】点D可能在点B的右边,也可能在点B的左边.
典例讲解:
题型一、等边三角形性质与判定的应用
例1、如图,等边△ABC中,AD是∠BAC的角平分线,E为AD上一点,以BE为一边且在BE下方作等边△BEF,连接CF.
求证:AE=CF;(2)求∠ACF的度数.
解题策略:题目中出现等边三角形是注意三个性质的应用。
如图,在△MNP中,∠P=60°,MN=NP,MQ⊥PN,垂足为Q,延长MN至点G,使NG=NQ.若△MNP的周长为12,MQ=a,则△MGQ的周长是 ( )
A.8+2a B.8+a C.6+a D.6+2a
2、如图,在四边形ABCD中,AB=AD,AB⊥BC,AD⊥DC,∠BAD=60°,点M,N分别在AB,AD边上,MC=NC.求证:△AMN是等边三角形.
题型二、等边三角形中的动点问题
例2、如图,在△ABC中,AB=BC=AC=12 cm,现有两点M,N分别从点A,B同时出发,沿三角形的边运动.已知点M的速度为1 cm/s,点N的速度为2 cm/s.当点M第一次到达点C时,M,N同时停止运动.
(1)点M,N运动多长时间后,M,N两点恰好重合
(2)点M,N运动多长时间后,△AMN是等边三角形
解题策略:根据题干分类讨论,利用等边建立方程求解。
变式练习:
3、如图1,等边△ABC中,D是AB边上的动点,以CD为一边,向上作等边△EDC,连接AE.
(1)△DBC和△EAC会全等吗?请说说你的理由;
(2)试说明AE∥BC的理由;
(3)如图2,当图1中动点D运动到边BA的延长线上时,所作仍为等边三角形,请问是否仍有AE∥BC?证明你的猜想.
当堂练习:
如图,ΔABC是等边三角形,AD⊥BC于点D,若AB=4,则BD= ,∠BAD=______
2.如图,在ΔABC中,BC的垂直平分线分别交BC,AB于点F,E.若ΔAEC是等边三角形,则∠B= ________
3.如图,P,Q是ΔABC的边BC上的两点,且BP=PQ=QC=AP=AQ,则∠BAC的大小是_________
4.如图,直线a,b分别经过等边三角形ABC的顶点A和C,且a//b,∠1=42°,则∠2的度数为:_____
如图,在等边ΔABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F.
(1)求证:AD=CE;(2)求∠DFC的度数.
6.如图,在一个池塘两旁有一条笔直小路(B,C为小路端点)和一棵小树(A为小树位置).测得的相关数据为:∠ABC=60°,∠ACB=60°,BC=48m,则AC= m.
7.如图,ΔABC是等边三角形,D,E,F分别是AB,BC,CA边上一点,且AD=BE=CF.判断DEF的形状并证明你的结论.
8.如图,在ΔABC中,∠BAC=120°,AD平分∠BAC,DE//AB,AD=3,CE=5,则AC的长为( B )A.9 B.8 C.6 D.7
9.【经典题】如图,ZAOB=60°,OA=OB,C为线段OB上一点,以AC为边在右侧作等边ΔACD,连接BD.(1)求证:DB//OA;(2)探究AB,CB与BD之间的数量关系,说明理由.
10.【经典题】如图,在等边ΔABC中,DE//BC交AB于点D,交AC于点E,延长DE至点F,CG⊥DF于点G,且DG=FG.
(1)求证:BD=CE;(2)求证:EF=BC.
11.(1)【问题背景】如图1,ΔABC为等边三角形,D为AB上一点,F为BC延长线上一点,AD=CF,连接DF交AC于点E,为了探究DE与EF的数量关系,小明同学发现在AC上截取AM=AD,连接DM,可以找到解题思路,请你直接写出DE与EF的数量关系.
(2)【变式应用】如图2,ΔABC为等边三角形,E为AC上一点,F为BC延长线上一点,AE=CF,连接BE.求证:BE=EF.
(3)【拓展创新】如图3,在ΔABC中,∠ABC=60°,∠BAC=80°,AD平分∠BAC,CD平分∠ACB.求证:AB=CD.
答案:
知识要点:
等边三角形的性质:(1)等边三角形的三个内角都 相等,并且每一个内角都等于 60° ;(2)等边三角形是 轴对称 图形,它有 3条对称轴.
2.等边三角形的判定:(1)三条边都 相等 的三角形是等边三角形;(2)三个角都 相等 的三角形是等边三角形;(3)有一个角是 60° 的等腰三角形是等边三角形.
易错点睛:
如图,等边ΔABC的边长为6,点D为直线BC上一点,BD=2,DE//AB交直线AC于点E,则DE的长为4或8
【点睛】点D可能在点B的右边,也可能在点B的左边.
典例讲解:
题型一、等边三角形性质与判定的应用
例1、如图,等边△ABC中,AD是∠BAC的角平分线,E为AD上一点,以BE为一边且在BE下方作等边△BEF,连接CF.
求证:AE=CF;(2)求∠ACF的度数.
解:(1)证明:∵△ABC是等边三角形,∴AB=BC,∠ABE+∠EBC=60°.∵△BEF是等边三角形,
∴EB=BF,∠CBF+∠EBC=60°.∴∠ABE=∠CBF.在△ABE和△CBF中,,
∴△ABE≌△CBF(SAS).∴AE=CF.
(2)∵等边△ABC中,AD是∠BAC的角平分线,∴∠BAE=30°,∠ACB=60°.∵△ABE≌△CBF,∴∠BCF=∠BAE=30°.∴∠ACF=∠BCF+∠ACB=30°+60°=90°.
解题策略:题目中出现等边三角形是注意三个性质的应用。
1、如图,在△MNP中,∠P=60°,MN=NP,MQ⊥PN,垂足为Q,延长MN至点G,使NG=NQ.若△MNP的周长为12,MQ=a,则△MGQ的周长是 ( )D
A.8+2a B.8+a C.6+a D.6+2a
2、如图,在四边形ABCD中,AB=AD,AB⊥BC,AD⊥DC,∠BAD=60°,点M,N分别在AB,AD边上,MC=NC.求证:△AMN是等边三角形.
证明:如图,连接AC.∵AB⊥BC,AD⊥DC,∴∠B=∠D=90°.
在Rt△ABC与Rt△ADC中,
∴Rt△ABC≌Rt△ADC(HL).∴BC=DC.
在Rt△MBC与Rt△NDC中,
∴Rt△MBC≌Rt△NDC(HL).∴BM=DN.
∵AB=AD,∴AM=AN.
又∵∠BAD=60°,∴△AMN是等边三角形.
题型二、等边三角形中的动点问题
例2、如图,在△ABC中,AB=BC=AC=12 cm,现有两点M,N分别从点A,B同时出发,沿三角形的边运动.已知点M的速度为1 cm/s,点N的速度为2 cm/s.当点M第一次到达点C时,M,N同时停止运动.
(1)点M,N运动多长时间后,M,N两点恰好重合
(2)点M,N运动多长时间后,△AMN是等边三角形
解:(1)设点M,N运动x s后,M,N两点恰好重合.由题意,得x×1+12=2x,解得x=12.
∴点M,N运动12 s后,M,N两点恰好重合.
(2)设点M,N运动t s后,△AMN是等边三角形,如图.由题意,得AM=t×1=t(cm),AN=AB-BN=(12-2t)cm.∵△AMN是等边三角形,∴t=12-2t,解得t=4.
∴点M,N运动4 s后,△AMN是等边三角形.
解题策略:根据题干分类讨论,利用等边建立方程求解。
变式练习:
3、如图1,等边△ABC中,D是AB边上的动点,以CD为一边,向上作等边△EDC,连接AE.
(1)△DBC和△EAC会全等吗?请说说你的理由;
(2)试说明AE∥BC的理由;
(3)如图2,当图1中动点D运动到边BA的延长线上时,所作仍为等边三角形,请问是否仍有AE∥BC?证明你的猜想.
解:(1)△DBC和△EAC全等.
理由:∵∠ACB=60°,∠DCE=60°,∴∠BCD=60°-∠ACD,∠ACE=60°-∠ACD,即∠BCD=∠ACE.在△DBC和△EAC中,,∴△DBC≌△EAC(SAS).
∵△DBC≌△EAC,∴∠EAC=∠B=60°.又∵∠ACB=60°,∴∠EAC=∠ACB.∴AE∥BC.(3)结论:AE∥BC.理由:∵△ABC、△EDC为等边三角形,∴BC=AC,DC=CE,∠BCA=∠DCE=60.∴∠BCA+∠ACD=∠DCE+∠ACD,即∠BCD=∠ACE.
在△DBC和△EAC中,,∴△DBC≌△EAC(SAS).∴∠EAC=∠B=60°.又∵∠ACB=60°,∴∠EAC=∠ACB.∴AE∥BC.
当堂练习:
如图,ΔABC是等边三角形,AD⊥BC于点D,若AB=4,则BD= 2,∠BAD= 30°
2.如图,在ΔABC中,BC的垂直平分线分别交BC,AB于点F,E.若ΔAEC是等边三角形,则∠B=30°
3.如图,P,Q是ΔABC的边BC上的两点,且BP=PQ=QC=AP=AQ,则∠BAC的大小是_120°
4.如图,直线a,b分别经过等边三角形ABC的顶点A和C,且a//b,∠1=42°,则∠2的度数为:_____1020
如图,在等边ΔABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F.
(1)求证:AD=CE;(2)求∠DFC的度数.
解:(1)证明略;
(2)∠DFC=60°.
如图,在一个池塘两旁有一条笔直小路(B,C为小路端点)和一棵小树(A为小树位置).测得的相关数据为:∠ABC=60°,∠ACB=60°,BC=48m,则AC=48m.
如图,ΔABC是等边三角形,D,E,F分别是AB,BC,CA边上一点,且AD=BE=CF.判断DEF的形状并证明你的结论.
解:ΔDEF是等边三角形.
∵ΔABC为等边三角形,且AD=BE,
∴AF=BD,∠A=∠B=60°,
∴ΔADF≌ΔBED(SAS).
同理证得ΔADF≌ΔCFE(SAS),
∴ΔADF≌ΔBED≌ΔCFE(SAS),∴DF=ED=EF,:∴ΔDEF是等边三角形.
如图,在ΔABC中,∠BAC=120°,AD平分∠BAC,DE//AB,AD=3,CE=5,则AC的长为( B )A.9 B.8 C.6 D.7
【经典题】如图,ZAOB=60°,OA=OB,C为线段OB上一点,以AC为边在右侧作等边ΔACD,连接BD.(1)求证:DB//OA;(2)探究AB,CB与BD之间的数量关系,说明理由.
证明:(1)易证ΔAOB为等边三角形,∴AB=OA,∠OAB=60°,易证ΔAOC≌ΔABD,
∴∠ABD=∠AOB=60°=∠OAB,
∴BD//OA;
(2)CB+BD=AB,理由如下:ΔAOC≌ΔABD,∴BD=OC,∴CB+BD=CB+OC=OB=AB.
10.【经典题】如图,在等边ΔABC中,DE//BC交AB于点D,交AC于点E,延长DE至点F,CG⊥DF于点G,且DG=FG.
(1)求证:BD=CE;(2)求证:EF=BC.
证明:(1)易证ΔADE是等边三角形,∴AD=AE,∵AB=AC,∴BD=CE;
(2)连接CD,∵CG⊥DF,DG=FG,∴CF=CD,
设∠F=∠CDF=x,
则∠BDC=180°-∠ADC
=180°-(60°+x)=120°-x,
∠ECF=∠ECG+∠GCF=30°+(90°-x)=120°-x,
∴∠BDC=∠ECF,:.ΔBDC≌ΔECF,∴EF=BC.
11.(1)【问题背景】如图1,ΔABC为等边三角形,D为AB上一点,F为BC延长线上一点,AD=CF,连接DF交AC于点E,为了探究DE与EF的数量关系,小明同学发现在AC上截取AM=AD,连接DM,可以找到解题思路,请你直接写出DE与EF的数量关系.
(2)【变式应用】如图2,ΔABC为等边三角形,E为AC上一点,F为BC延长线上一点,AE=CF,连接BE.求证:BE=EF.
(3)【拓展创新】如图3,在ΔABC中,∠ABC=60°,∠BAC=80°,AD平分∠BAC,CD平分∠ACB.求证:AB=CD.
解:(1)DE=EF;
(2)在AB上截取AD=AE,连接DE.
∵ΔABC为等边三角形,
∴∠ACB=∠A=60°,AB=AC.
∵AD=AE,∴ΔADE为等边三角形.∴DE=AD=AE,∠ADE=60°
∵AE=CF,AB=AC,∠ACB=60°,
∴DE=CF,BD=CE,∠BDE=∠ECF=120°
∴ΔBDE≌ΔECF,∴BE=EF;
(3)证明:在BC上截取BE=AB,连接AE.∵∠ABC=60°,
∴ΔABE为等边三角形.
∴AB=AE,∠BAE=60°.∵∠ABC=60°,∠BAC=80°,∴∠EAC=∠BAC-∠BAE=20°,∠ACB=40°. :∵AD平分∠BAC,CD平分∠ACB,.
∴∠BAD=∠CAD=40°,∠ACD=∠BCD=20°.
∴∠DAC=∠ACB=40°,∠ACD=∠EAC=20°.
∵AC=CA,∴ΔACD≌ΔCAE, ∴CD=AE.∵AE=AB,∴AB=CD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
