华东师大版数学八年级上册 13.2.4 角边角 课件(共20张PPT)
文档属性
| 名称 | 华东师大版数学八年级上册 13.2.4 角边角 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 412.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-05 00:00:00 | ||
图片预览



文档简介
(共20张PPT)
角边角
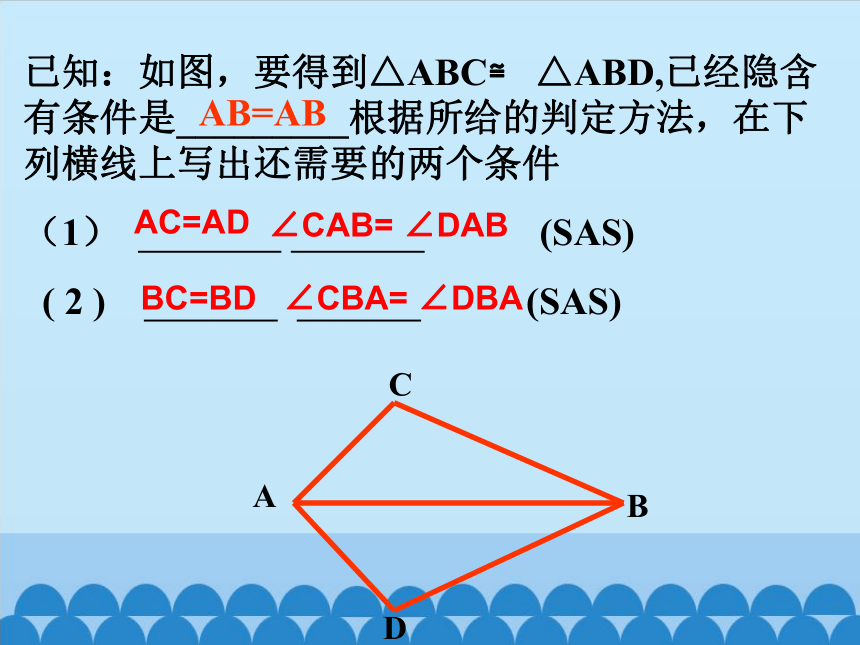
已知:如图,要得到△ABC≌ △ABD,已经隐含有条件是_________根据所给的判定方法,在下列横线上写出还需要的两个条件
(1) (SAS)
( 2 ) (SAS)
A
B
C
D
AB=AB
AC=AD
∠CAB= ∠DAB
BC=BD
∠CBA= ∠DBA
当两个三角形的两条边及其夹角分别对应相等时,
两个三角形一定全等.(SAS)
而当两个三角形的两条边及其中一边的对角分别对应
相等时,两个三角形未必一定全等.(SSA)
两角一边呢
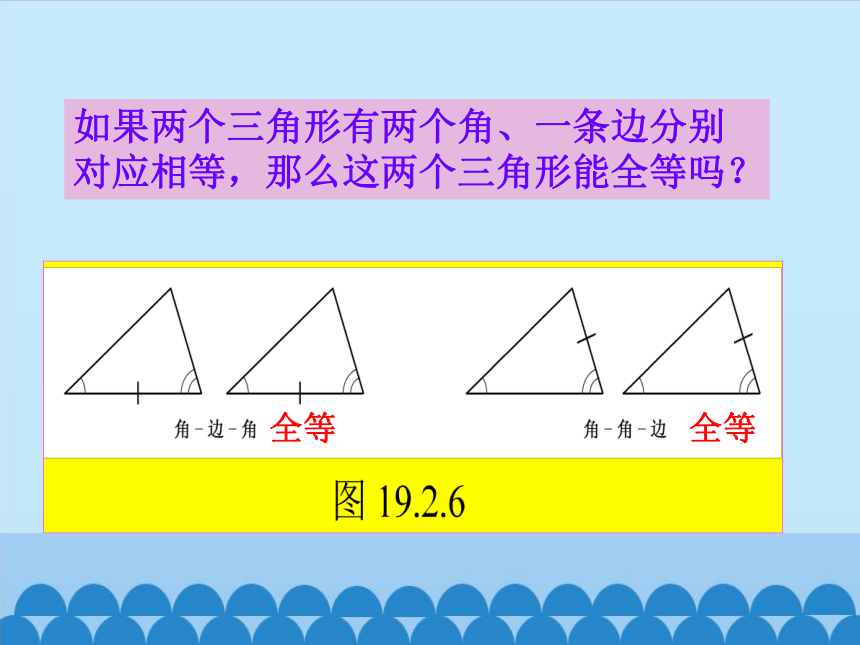
如果两个三角形有两个角、一条边分别
对应相等,那么这两个三角形能全等吗?
全等
全等
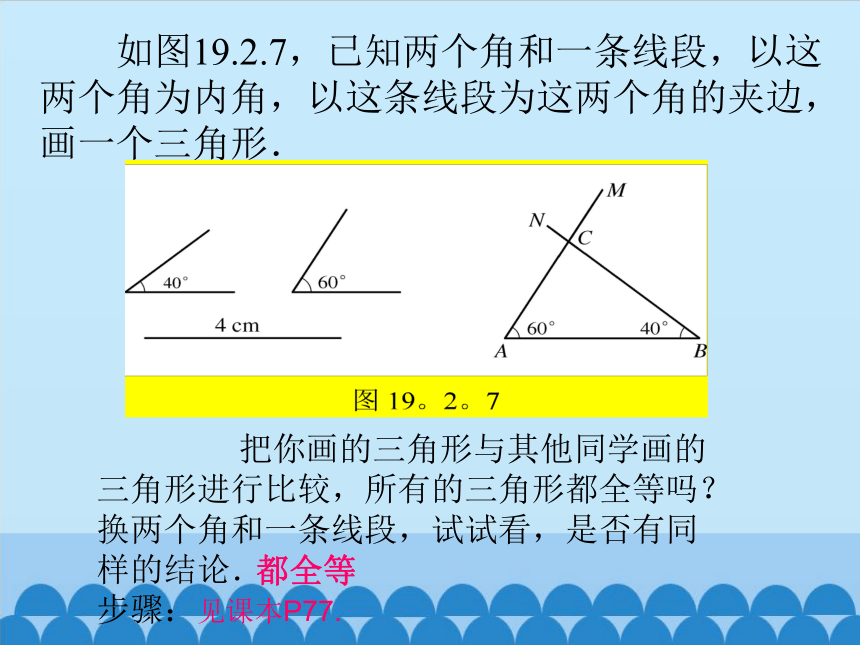
如图19.2.7,已知两个角和一条线段,以这
两个角为内角,以这条线段为这两个角的夹边,
画一个三角形.
把你画的三角形与其他同学画的
三角形进行比较,所有的三角形都全等吗?
换两个角和一条线段,试试看,是否有同
样的结论.
步骤:见课本P77.
都全等
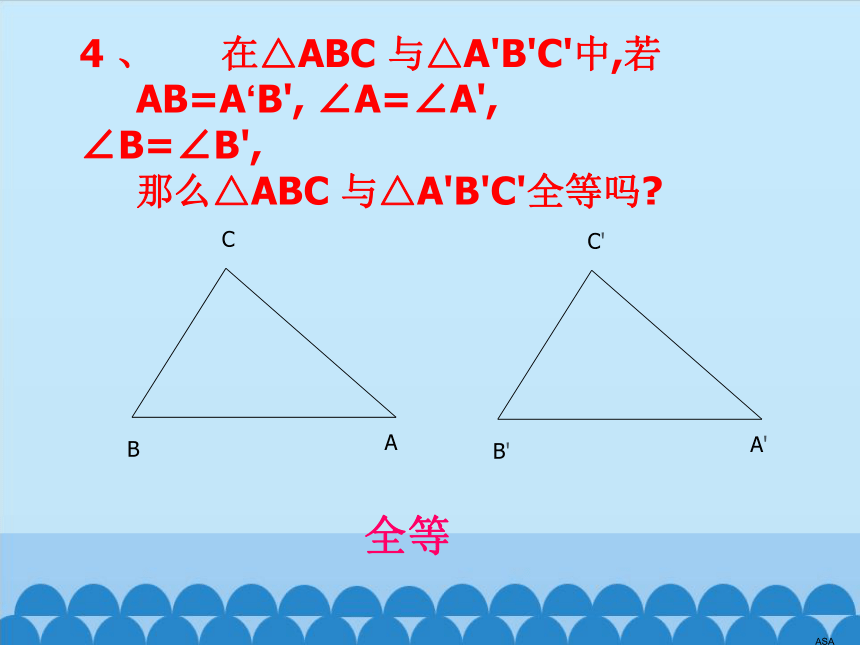
4 、 在△ABC 与△A'B'C'中,若
AB=A‘B', ∠A=∠A', ∠B=∠B',
那么△ABC 与△A'B'C'全等吗
C
B
A
C'
B'
A'
ASA
全等
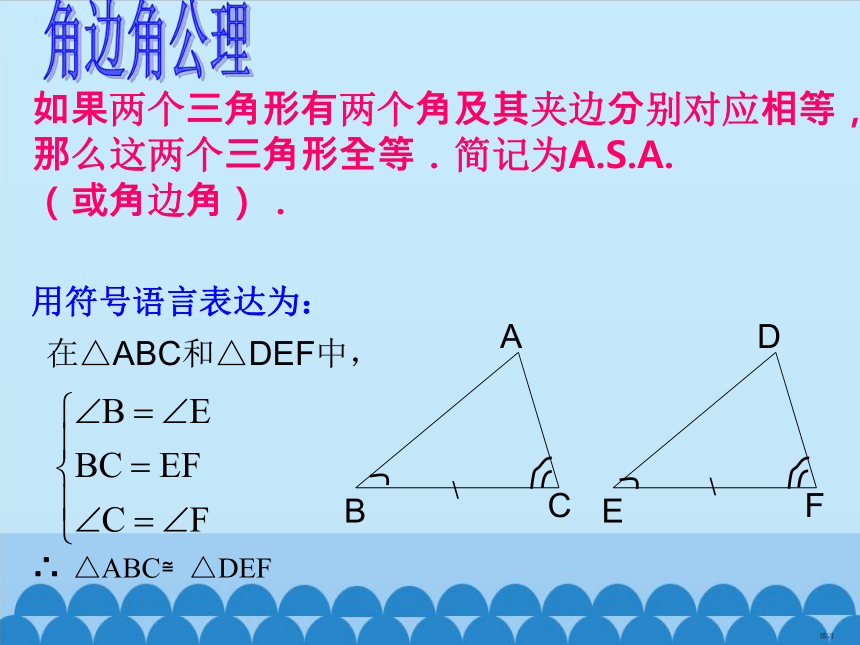
如果两个三角形有两个角及其夹边分别对应相等,那么这两个三角形全等.简记为A.S.A.
(或角边角).
角边角公理
在△ABC和△DEF中,
△ABC≌△DEF
∴
用符号语言表达为:
D
E
F
A
B
C
练习
如图,要证明△ACE≌ △BDF,根据给定的条件和指明的依据,将应当添设的条件填在横线上。
(1)AC∥BD,CE=DF, (SAS)
( 2) AC=BD, AC∥BD (ASA)
( 3) CE=DF, (ASA)
( 4)∠ C= ∠D, (ASA)
C
B
A
E
F
D
课堂练习
∠AEC=∠BFD
AC=BD
∠A=∠B
∠C=∠D
AC=BD
∠A=∠B
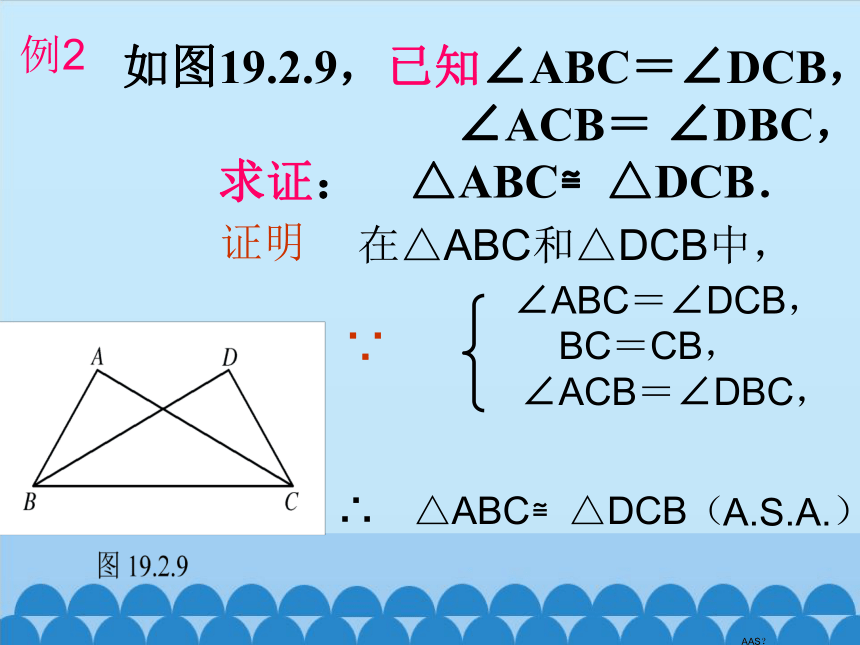
如图19.2.9,已知∠ABC=∠DCB,
∠ACB= ∠DBC,
求证: △ABC≌△DCB.
例2
∠ABC=∠DCB,
BC=CB,
∠ACB=∠DBC,
证明
在△ABC和△DCB中,
∵
∴ △ABC≌△DCB( )
A.S.A.
AAS?
P74练习 1、如图,已知∠ABC=∠D,∠ACB=∠CBD
判断图中的两个三角形是否全等,并说明理由.
不全等。因为虽然有两组内角相等,且BC=BC,但不都是两个三角形两组内角的夹边,所以不全等。
如图:如果两个三角形有两个角及其中一个角的对
边分别对应相等,那么这两个三角形是否一定全等?
已知:∠A=∠A′, ∠B=∠B′, AC=A′C′
求证: △ABC≌△A′B′C′
证明∵ ∠A=∠A′, ∠B=∠B′
又∠A+∠B+∠C=180°
(三角形的内角和等于180°)
同理∠A′+∠B′+∠C′=180°
∴ ∠C=∠C′.
在△ABC和△A′B′C′中
∵ ∠A=∠A′
AC=A′C′
∠C=∠C′
∴ △ABC≌△A′B′C′(A.S.A.)
定理:
如果两个三角形有两个角和其中
一个角的对边分别对应相等,那么这两个三角形全等.简记为A.A.S.(或角角边).
D
E
F
A
B
C
P74练习2、如图,△ABC是等腰三角形,AD、 BE分别是
∠BAC、∠ABC的角平分线,△ABD和△BAE全等吗?
试说明理由.
全等。∵ △ABC是等腰三角形
∴ ∠ABD=∠BAE
∵ AD、 BE分别是
∠BAC、∠ABC的角平分线
∴ ∠BAD=∠ABE=等腰△ABC底角的一半
∵AB=BA
∴ △ABD≌△BAE(ASA)
练一练
已知: △ABC和△ A′B′C′中,AB=A′B′,
∠A=∠A′,∠B=∠B′,
则△ABC≌△ A′B′C′的根据是( )
A; SAS B: ASA C: AAS D:都不对
B
D
已知: △ABC和△A′B′C ′中,AB=A′B′,
∠A=∠A′, 若△ABC≌△ A′B′C′,
还需要什么条件( )
A:∠B=∠B′ B: ∠C=∠C′
C: AC=A′C′ D: A、B、C均可
A
B
C
A′
B′
C′
口答:
1.两个直角三角形中,斜边和一锐角对应相等,这两个直角
三角形全等吗?为什么?
2.两个直角三角形中,有一条直角边和一锐角对应相等,这
两个直角三角形全等吗?为什么?
答:全等,根据AAS
答:全等,根据AAS
如图,已知AB=AC,∠ADB= ∠AEC,求证:
△ABD≌△ACE
A
B
C
D
E
证明:∵ AB=AC,
∴ ∠B= ∠C(等边对等角)
∵ ∠ADB= ∠AEC, AB=AC,
∴ △ABD≌△ACE(AAS)
如图,O是AB的中点, = , 与 全等吗
为什么?
两角和夹边对应相等
(已知)
(中点的定义)
(对顶角相等)
在 和 中
( )
已知如图,∠1 = ∠2,∠C = ∠D
求证:AC = AD
A
B
D
C
2
1
证明:在△ABC和△ABD中
∠1 = ∠2
∠C = ∠D
AB = AB
∴△ABC≌△ABD(AAS)
∴AC = AD(全等三角形对应边相等)
谈谈本节课的收获
小结
谢谢!
角边角
已知:如图,要得到△ABC≌ △ABD,已经隐含有条件是_________根据所给的判定方法,在下列横线上写出还需要的两个条件
(1) (SAS)
( 2 ) (SAS)
A
B
C
D
AB=AB
AC=AD
∠CAB= ∠DAB
BC=BD
∠CBA= ∠DBA
当两个三角形的两条边及其夹角分别对应相等时,
两个三角形一定全等.(SAS)
而当两个三角形的两条边及其中一边的对角分别对应
相等时,两个三角形未必一定全等.(SSA)
两角一边呢
如果两个三角形有两个角、一条边分别
对应相等,那么这两个三角形能全等吗?
全等
全等
如图19.2.7,已知两个角和一条线段,以这
两个角为内角,以这条线段为这两个角的夹边,
画一个三角形.
把你画的三角形与其他同学画的
三角形进行比较,所有的三角形都全等吗?
换两个角和一条线段,试试看,是否有同
样的结论.
步骤:见课本P77.
都全等
4 、 在△ABC 与△A'B'C'中,若
AB=A‘B', ∠A=∠A', ∠B=∠B',
那么△ABC 与△A'B'C'全等吗
C
B
A
C'
B'
A'
ASA
全等
如果两个三角形有两个角及其夹边分别对应相等,那么这两个三角形全等.简记为A.S.A.
(或角边角).
角边角公理
在△ABC和△DEF中,
△ABC≌△DEF
∴
用符号语言表达为:
D
E
F
A
B
C
练习
如图,要证明△ACE≌ △BDF,根据给定的条件和指明的依据,将应当添设的条件填在横线上。
(1)AC∥BD,CE=DF, (SAS)
( 2) AC=BD, AC∥BD (ASA)
( 3) CE=DF, (ASA)
( 4)∠ C= ∠D, (ASA)
C
B
A
E
F
D
课堂练习
∠AEC=∠BFD
AC=BD
∠A=∠B
∠C=∠D
AC=BD
∠A=∠B
如图19.2.9,已知∠ABC=∠DCB,
∠ACB= ∠DBC,
求证: △ABC≌△DCB.
例2
∠ABC=∠DCB,
BC=CB,
∠ACB=∠DBC,
证明
在△ABC和△DCB中,
∵
∴ △ABC≌△DCB( )
A.S.A.
AAS?
P74练习 1、如图,已知∠ABC=∠D,∠ACB=∠CBD
判断图中的两个三角形是否全等,并说明理由.
不全等。因为虽然有两组内角相等,且BC=BC,但不都是两个三角形两组内角的夹边,所以不全等。
如图:如果两个三角形有两个角及其中一个角的对
边分别对应相等,那么这两个三角形是否一定全等?
已知:∠A=∠A′, ∠B=∠B′, AC=A′C′
求证: △ABC≌△A′B′C′
证明∵ ∠A=∠A′, ∠B=∠B′
又∠A+∠B+∠C=180°
(三角形的内角和等于180°)
同理∠A′+∠B′+∠C′=180°
∴ ∠C=∠C′.
在△ABC和△A′B′C′中
∵ ∠A=∠A′
AC=A′C′
∠C=∠C′
∴ △ABC≌△A′B′C′(A.S.A.)
定理:
如果两个三角形有两个角和其中
一个角的对边分别对应相等,那么这两个三角形全等.简记为A.A.S.(或角角边).
D
E
F
A
B
C
P74练习2、如图,△ABC是等腰三角形,AD、 BE分别是
∠BAC、∠ABC的角平分线,△ABD和△BAE全等吗?
试说明理由.
全等。∵ △ABC是等腰三角形
∴ ∠ABD=∠BAE
∵ AD、 BE分别是
∠BAC、∠ABC的角平分线
∴ ∠BAD=∠ABE=等腰△ABC底角的一半
∵AB=BA
∴ △ABD≌△BAE(ASA)
练一练
已知: △ABC和△ A′B′C′中,AB=A′B′,
∠A=∠A′,∠B=∠B′,
则△ABC≌△ A′B′C′的根据是( )
A; SAS B: ASA C: AAS D:都不对
B
D
已知: △ABC和△A′B′C ′中,AB=A′B′,
∠A=∠A′, 若△ABC≌△ A′B′C′,
还需要什么条件( )
A:∠B=∠B′ B: ∠C=∠C′
C: AC=A′C′ D: A、B、C均可
A
B
C
A′
B′
C′
口答:
1.两个直角三角形中,斜边和一锐角对应相等,这两个直角
三角形全等吗?为什么?
2.两个直角三角形中,有一条直角边和一锐角对应相等,这
两个直角三角形全等吗?为什么?
答:全等,根据AAS
答:全等,根据AAS
如图,已知AB=AC,∠ADB= ∠AEC,求证:
△ABD≌△ACE
A
B
C
D
E
证明:∵ AB=AC,
∴ ∠B= ∠C(等边对等角)
∵ ∠ADB= ∠AEC, AB=AC,
∴ △ABD≌△ACE(AAS)
如图,O是AB的中点, = , 与 全等吗
为什么?
两角和夹边对应相等
(已知)
(中点的定义)
(对顶角相等)
在 和 中
( )
已知如图,∠1 = ∠2,∠C = ∠D
求证:AC = AD
A
B
D
C
2
1
证明:在△ABC和△ABD中
∠1 = ∠2
∠C = ∠D
AB = AB
∴△ABC≌△ABD(AAS)
∴AC = AD(全等三角形对应边相等)
谈谈本节课的收获
小结
谢谢!
