2021-2022学年高一下学期数学人教A版(2019)必修第二册9.2.3总体集中趋势的估计教学设计
文档属性
| 名称 | 2021-2022学年高一下学期数学人教A版(2019)必修第二册9.2.3总体集中趋势的估计教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 247.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-04 00:00:00 | ||
图片预览



文档简介
9.2.3总体集中趋势的估计(第一课时)
(人教A版普通高中教科书数学必修第二册第九章)
一、教学目标
1.会求样本的众数、中位数、平均数;
2.会应用相关知识解决实际统计问题.
二、教学重难点
1.通过数字特征的计算,提升数学运算素养.
2.借助实际统计问题的应用,培养数学建模素养.
三、教学过程
1.样本集中趋势概念的形成
1.1创设情境,引发思考
【情境引入】现从甲、乙、丙三个厂家生产的同一种耐用家电产品中,各抽取8件产品,对其使用寿命进行跟踪调查,其结果如下:(单位:年)
甲: 3,4,5,6,8,8,8,10; 乙:4,6,6,6,8,9,12,13;
丙:3,3,4,7,9,10,11,12.
问题1: 三家广告中都称其产品的使用寿命为8年,利用初中所学的知识,你能说明为什么吗?
【预设的答案】三个产家是从不同角度进行了说明,以宣传自己的产品。其中甲:众数为8年 ,乙的平均数是8年,丙:中位数为8年。
【设计意图】从现实生活中是广告知识引出样本集中趋势估计中的平均数、中位数、众数的知识,让学生感受样本集中趋势的估计这样的问题是客观存在的,是源于实际生活的.
问题2:结合初中学过的知识,请你写出平均数、中位数、众数的定义?
【预设的答案】
1.众数:一组数据中出现次数最多的数.
2.中位数:把一组数据按从小到大的顺序排列,处在中间位置的数(或中间两个数的平均数)叫做这组数据的中位数.即第50百分位数.
3.平均数:如果n个数x1,x2,…,xn,那么叫做这n个数的平均数.
1.2探究典例,形成概念
活动:预习课本P203-P208 页回答下列问题。
【活动预设】感受在求平均数、中位数和众数的过程中,理解众数、中位数、平均数的意义.
【设计意图】为引入直方图中求平均数、中位数和众数做铺垫.
问题1:利用9.2.1节中100户居民的月均用水量的调查数据,计算样本数据的平均数和中位数,并据此估计全市居民用户月均用水量的平均数和中位数.
【活动预设】
(1)利用excel表格计算出100个数据的平均数、中位数;
(2)预设的答案:根据样本平均数的定义,可得即100户居民的月均用水量的平均数为8.79t. 将样本数据按从小到大排序,得第50个数和51个数分别是6.4,6.8,用中位数的定义,可得,即100户居民的月均用水量的中位数是6.6t.
据此估计全市居民用户的月均用水量约为8.79t,其中中位数约为6.6t.
【设计意图】从引例中的具体问题入手,让学生学会处理数学数据的能力.
思考1:小明用统计软件计算了100户居民用水量的平均数和中位数。但在录入数据时,不小心把一个数据7.7录成了77.请计算录入数据的平均数和中位数,并与真实的样本平均数和中位数作比较.哪个量的值变化更大?你能解释其中的原因吗?
【活动预设】
(1)分析个别数据的变化,对平均数和中位数是否有影响;
(2)感受:个别数据的变化,对于平均数的影响是比较大的,但是对于中位数的影响不是很大.
教师小结:因为样本平均数与每一个样本数据有关,样本中的任何一个数据的改变都会引起平均数的改变;但中位数只利用了样本数据中间位置的一个或两个值,并未利用其它数据,所以不是任何一个样本数据的改变都会引起中位数的改变.
因此,与中位数比较,平均数反映出样本数据中的更多信息,对样本中的极端值更加敏感.
【设计意图】通过改变数据,求出新的平均数和中位数,通过新旧数据的对比,了解平均数反映出样本数据中的更多信息,对样本中的极端值更加敏感.
跟踪训练1:在一次中学生田径运动会上,参加男子跳高的17名运动员的成绩如表所示:
成绩(单位:m) 1.50 1.60 1.65 1.70 1.75 1.80 1.85 1.90
人数 2 3 2 3 4 1 1 1
分别求出这些运动员成绩的众数、中位数与平均数.
【预设的答案】在17个数据中,1.75出现了4次,出现的次数最多,即这组数据的众数是1.75.
上面表里的17个数据可看成是按从小到大的顺序排列的,其中第9个数据1.70是最中间的一个数据,即这组数据的中位数是1.70.
这组数据的平均数是
故17名运动员成绩的众数、中位数、平均数依次为1.75m,1.70m,1.69m.
【设计意图】
(1)根据定义求出平均数、众数中位数;
(2)理解众数、中位数和平均数的定义及计算方式.
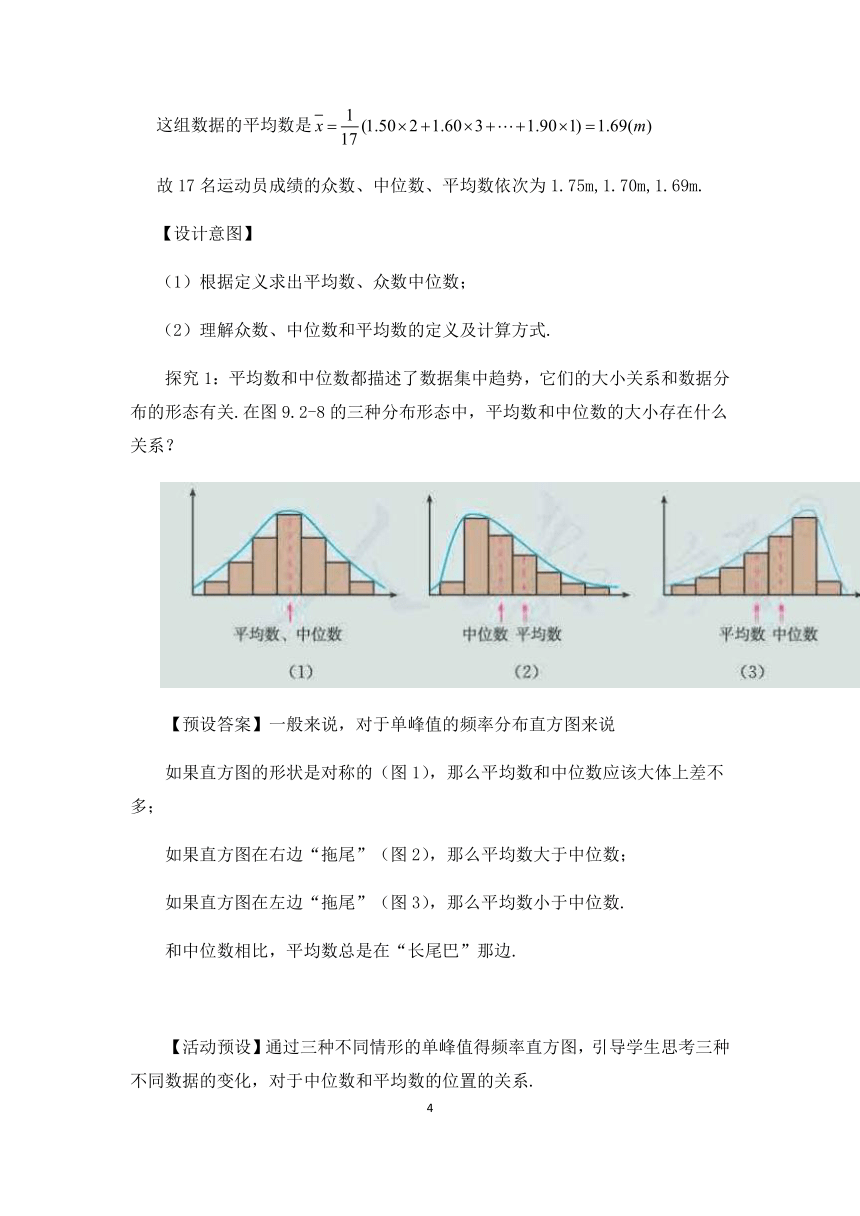
探究1:平均数和中位数都描述了数据集中趋势,它们的大小关系和数据分布的形态有关.在图9.2-8的三种分布形态中,平均数和中位数的大小存在什么关系?
【预设答案】一般来说,对于单峰值的频率分布直方图来说
如果直方图的形状是对称的(图1),那么平均数和中位数应该大体上差不多;
如果直方图在右边“拖尾”(图2),那么平均数大于中位数;
如果直方图在左边“拖尾”(图3),那么平均数小于中位数.
和中位数相比,平均数总是在“长尾巴”那边.
【活动预设】通过三种不同情形的单峰值得频率直方图,引导学生思考三种不同数据的变化,对于中位数和平均数的位置的关系.
【设计意图】
在形成概念后,在实践活动中进行再认识,熟悉概念,从外延的角度加深概念的理解,为下一个环节作铺垫.
例2 某学校要定制高一年级的校服,学生根据厂家提供的参考身高选择校服的规格.据统计,高一年级女生需要不同规格校服的频数如下表
如果用一个量来代表该校高一年级女生所需校服的规格,那么在中位数、平均数和众数中,哪个量比较合适?试讨论用表中的数据估计全国高一女生校服规格的合理性.
【活动预设】
引导学生通过对平均数、众数和中位数的求解,根据实际问题利用样本集中趋势来估算并解决实际问题.
【设计意图】
从感知个例到分析通例,遵循从特殊到一般的思路,在具体实践的基础上进行理性分析,认识样本集中趋势在现实生活中我运用,加深对众数、中位数和平均数概念外延的理解,为后续的学习作铺垫.
2.求解直方图的平均数、众数和中位数
探究2:你能以100户居民月均用水量的频率分布直方图提供的信息为例,给出估计的方法吗?
【预设的答案】
(1)平均数:
(2)中位数:根据中位数的意义,在样本中,有 的个体小于或等于中位数,也有50的个体大于或等于中位数.因此在频率分布直方图中,中位数左边和右边的直方图面积应该相等.
(
0.077x3+0.107x(
-0.42)=0.5,
可得
6.71
)中位数落在[4.2,7.2)内,设中位数为x,由
(3)众数:根据频率分布直方图,月均用水量在区间[4.2,7.2)内居民最多,可以将这个区间的中点5.7作为众数的估计值.
【设计意图】
(1)通过前面例子的方法求出平均数,通过观察发现其中100是可以约去的.
(2)通过变形可以发现直方图中求样本平均数可以用每一个小矩形底边中点的横坐标与小矩形的面积的乘积之和近似值代替.
(3)根据中位数的定义,中位数即为50百分位数,进而给出中位数的求法
思考2:众数、中位数、平均数与频率分布直方图之间有什么联系
【预设的答案】
(1)众数:众数在样本数据的频率分布直方图中,就是最高矩形的底边中点的横坐标.
(2)中位数:咋样本中50的个体大于或等于中位数。因此,在频率分布直方图中,中位数左边和右边的直方图的面积应该相等.由此可估计中位数的值.
(3)平均数:用频率分布直方图估计平均数时,平均数等于频率分布直方图中每个小矩形的面积乘以每个小矩形底边中点的横坐标之和.
【设计意图】
(1)通过学生小组讨论总结出样本集中趋势之间的联系;
(2)从实例求解中得出直方图中求平均数、中位数和众数的估算方法.
(3)比较三者之间的关系,进而对三者的概念更加清晰。
例3 某校从参加高一年级期末考试的学生中抽出60名,将其物理成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如图所示的频率分布直方图.观察图中的信息,回答下列问题:
估计这次考试的物理成绩的众数m与中位数n(结果保留一位小数);
(2)估计这次考试的物理成绩的及格率(60分及以上为及格)和平均分.
【预设的答案】
(1) 解 众数是频率分布直方图中最高小矩形底边中点的横坐标,所以众数为m=75.0.
前3个小矩形面积和为0.01×10+0.015×10+0.015×10=0.4<0.5,
前4个小矩形面积和为0.4+0.03×10=0.7>0.5,
所以中位数为
(2)依题意,60及60以上的分数在第三、四、五、六组,频率和为
(0.015+0.03+0.025+0.005)×10=0.75,
所以,估计这次考试的物理成绩的及格率是75%.
利用组中值估算抽样学生的平均分45×f1+55×f2+65×f3+75×f4+85×f5+95×f6
=45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71.
估计这次考试物理成绩的平均分是71分.
【设计意图】
在解题中加深对概念的理解,形成解题的基本思路:对直方图中求平均数、众数和中位数的掌握;形成解题的基本技能:恰当设数,然后利用中位数数的相关知识解题.
跟踪训练3:我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查.通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.估计居民月均用水量的中位数.
【预设的答案】
解:由(0.08+0.16+a+0.42+0.50+a+0.12+0.08+0.04)×0.5=1,
解得a=0.30.
因为前5组的频率之和为0.04+0.08+0.15+0.21+0.25=0.73>0.5.
而前4组的频率之和为0.04+0.08+0.15+0.21=0.48<0.5.
设中位数为x吨.
由0.50×(x-2)=0.5-0.48,解得x=2.04.
故可估计居民月均用水量的中位数为2.04吨.
【设计意图】加深对知识点的认识以及运用。
3.课堂小结
【预设的答案】
1.通过学习平均数、中位数和众数的计算级应用,重点培养数学运算素养及数据分析素养
2.一组数据中的众数可能不止一个,中位数是唯一的,求中位数时,必须先排序.
3.利用频率分布直方图求数字特征:
(1)众数是最高矩形的底边中点的横坐标.
(2)中位数左右两边直方图的面积应相等.
(3)平均数等于每个小矩形的面积乘以小矩形底边中点的横坐标之和.
四、课外作业
7
(人教A版普通高中教科书数学必修第二册第九章)
一、教学目标
1.会求样本的众数、中位数、平均数;
2.会应用相关知识解决实际统计问题.
二、教学重难点
1.通过数字特征的计算,提升数学运算素养.
2.借助实际统计问题的应用,培养数学建模素养.
三、教学过程
1.样本集中趋势概念的形成
1.1创设情境,引发思考
【情境引入】现从甲、乙、丙三个厂家生产的同一种耐用家电产品中,各抽取8件产品,对其使用寿命进行跟踪调查,其结果如下:(单位:年)
甲: 3,4,5,6,8,8,8,10; 乙:4,6,6,6,8,9,12,13;
丙:3,3,4,7,9,10,11,12.
问题1: 三家广告中都称其产品的使用寿命为8年,利用初中所学的知识,你能说明为什么吗?
【预设的答案】三个产家是从不同角度进行了说明,以宣传自己的产品。其中甲:众数为8年 ,乙的平均数是8年,丙:中位数为8年。
【设计意图】从现实生活中是广告知识引出样本集中趋势估计中的平均数、中位数、众数的知识,让学生感受样本集中趋势的估计这样的问题是客观存在的,是源于实际生活的.
问题2:结合初中学过的知识,请你写出平均数、中位数、众数的定义?
【预设的答案】
1.众数:一组数据中出现次数最多的数.
2.中位数:把一组数据按从小到大的顺序排列,处在中间位置的数(或中间两个数的平均数)叫做这组数据的中位数.即第50百分位数.
3.平均数:如果n个数x1,x2,…,xn,那么叫做这n个数的平均数.
1.2探究典例,形成概念
活动:预习课本P203-P208 页回答下列问题。
【活动预设】感受在求平均数、中位数和众数的过程中,理解众数、中位数、平均数的意义.
【设计意图】为引入直方图中求平均数、中位数和众数做铺垫.
问题1:利用9.2.1节中100户居民的月均用水量的调查数据,计算样本数据的平均数和中位数,并据此估计全市居民用户月均用水量的平均数和中位数.
【活动预设】
(1)利用excel表格计算出100个数据的平均数、中位数;
(2)预设的答案:根据样本平均数的定义,可得即100户居民的月均用水量的平均数为8.79t. 将样本数据按从小到大排序,得第50个数和51个数分别是6.4,6.8,用中位数的定义,可得,即100户居民的月均用水量的中位数是6.6t.
据此估计全市居民用户的月均用水量约为8.79t,其中中位数约为6.6t.
【设计意图】从引例中的具体问题入手,让学生学会处理数学数据的能力.
思考1:小明用统计软件计算了100户居民用水量的平均数和中位数。但在录入数据时,不小心把一个数据7.7录成了77.请计算录入数据的平均数和中位数,并与真实的样本平均数和中位数作比较.哪个量的值变化更大?你能解释其中的原因吗?
【活动预设】
(1)分析个别数据的变化,对平均数和中位数是否有影响;
(2)感受:个别数据的变化,对于平均数的影响是比较大的,但是对于中位数的影响不是很大.
教师小结:因为样本平均数与每一个样本数据有关,样本中的任何一个数据的改变都会引起平均数的改变;但中位数只利用了样本数据中间位置的一个或两个值,并未利用其它数据,所以不是任何一个样本数据的改变都会引起中位数的改变.
因此,与中位数比较,平均数反映出样本数据中的更多信息,对样本中的极端值更加敏感.
【设计意图】通过改变数据,求出新的平均数和中位数,通过新旧数据的对比,了解平均数反映出样本数据中的更多信息,对样本中的极端值更加敏感.
跟踪训练1:在一次中学生田径运动会上,参加男子跳高的17名运动员的成绩如表所示:
成绩(单位:m) 1.50 1.60 1.65 1.70 1.75 1.80 1.85 1.90
人数 2 3 2 3 4 1 1 1
分别求出这些运动员成绩的众数、中位数与平均数.
【预设的答案】在17个数据中,1.75出现了4次,出现的次数最多,即这组数据的众数是1.75.
上面表里的17个数据可看成是按从小到大的顺序排列的,其中第9个数据1.70是最中间的一个数据,即这组数据的中位数是1.70.
这组数据的平均数是
故17名运动员成绩的众数、中位数、平均数依次为1.75m,1.70m,1.69m.
【设计意图】
(1)根据定义求出平均数、众数中位数;
(2)理解众数、中位数和平均数的定义及计算方式.
探究1:平均数和中位数都描述了数据集中趋势,它们的大小关系和数据分布的形态有关.在图9.2-8的三种分布形态中,平均数和中位数的大小存在什么关系?
【预设答案】一般来说,对于单峰值的频率分布直方图来说
如果直方图的形状是对称的(图1),那么平均数和中位数应该大体上差不多;
如果直方图在右边“拖尾”(图2),那么平均数大于中位数;
如果直方图在左边“拖尾”(图3),那么平均数小于中位数.
和中位数相比,平均数总是在“长尾巴”那边.
【活动预设】通过三种不同情形的单峰值得频率直方图,引导学生思考三种不同数据的变化,对于中位数和平均数的位置的关系.
【设计意图】
在形成概念后,在实践活动中进行再认识,熟悉概念,从外延的角度加深概念的理解,为下一个环节作铺垫.
例2 某学校要定制高一年级的校服,学生根据厂家提供的参考身高选择校服的规格.据统计,高一年级女生需要不同规格校服的频数如下表
如果用一个量来代表该校高一年级女生所需校服的规格,那么在中位数、平均数和众数中,哪个量比较合适?试讨论用表中的数据估计全国高一女生校服规格的合理性.
【活动预设】
引导学生通过对平均数、众数和中位数的求解,根据实际问题利用样本集中趋势来估算并解决实际问题.
【设计意图】
从感知个例到分析通例,遵循从特殊到一般的思路,在具体实践的基础上进行理性分析,认识样本集中趋势在现实生活中我运用,加深对众数、中位数和平均数概念外延的理解,为后续的学习作铺垫.
2.求解直方图的平均数、众数和中位数
探究2:你能以100户居民月均用水量的频率分布直方图提供的信息为例,给出估计的方法吗?
【预设的答案】
(1)平均数:
(2)中位数:根据中位数的意义,在样本中,有 的个体小于或等于中位数,也有50的个体大于或等于中位数.因此在频率分布直方图中,中位数左边和右边的直方图面积应该相等.
(
0.077x3+0.107x(
-0.42)=0.5,
可得
6.71
)中位数落在[4.2,7.2)内,设中位数为x,由
(3)众数:根据频率分布直方图,月均用水量在区间[4.2,7.2)内居民最多,可以将这个区间的中点5.7作为众数的估计值.
【设计意图】
(1)通过前面例子的方法求出平均数,通过观察发现其中100是可以约去的.
(2)通过变形可以发现直方图中求样本平均数可以用每一个小矩形底边中点的横坐标与小矩形的面积的乘积之和近似值代替.
(3)根据中位数的定义,中位数即为50百分位数,进而给出中位数的求法
思考2:众数、中位数、平均数与频率分布直方图之间有什么联系
【预设的答案】
(1)众数:众数在样本数据的频率分布直方图中,就是最高矩形的底边中点的横坐标.
(2)中位数:咋样本中50的个体大于或等于中位数。因此,在频率分布直方图中,中位数左边和右边的直方图的面积应该相等.由此可估计中位数的值.
(3)平均数:用频率分布直方图估计平均数时,平均数等于频率分布直方图中每个小矩形的面积乘以每个小矩形底边中点的横坐标之和.
【设计意图】
(1)通过学生小组讨论总结出样本集中趋势之间的联系;
(2)从实例求解中得出直方图中求平均数、中位数和众数的估算方法.
(3)比较三者之间的关系,进而对三者的概念更加清晰。
例3 某校从参加高一年级期末考试的学生中抽出60名,将其物理成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如图所示的频率分布直方图.观察图中的信息,回答下列问题:
估计这次考试的物理成绩的众数m与中位数n(结果保留一位小数);
(2)估计这次考试的物理成绩的及格率(60分及以上为及格)和平均分.
【预设的答案】
(1) 解 众数是频率分布直方图中最高小矩形底边中点的横坐标,所以众数为m=75.0.
前3个小矩形面积和为0.01×10+0.015×10+0.015×10=0.4<0.5,
前4个小矩形面积和为0.4+0.03×10=0.7>0.5,
所以中位数为
(2)依题意,60及60以上的分数在第三、四、五、六组,频率和为
(0.015+0.03+0.025+0.005)×10=0.75,
所以,估计这次考试的物理成绩的及格率是75%.
利用组中值估算抽样学生的平均分45×f1+55×f2+65×f3+75×f4+85×f5+95×f6
=45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71.
估计这次考试物理成绩的平均分是71分.
【设计意图】
在解题中加深对概念的理解,形成解题的基本思路:对直方图中求平均数、众数和中位数的掌握;形成解题的基本技能:恰当设数,然后利用中位数数的相关知识解题.
跟踪训练3:我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查.通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.估计居民月均用水量的中位数.
【预设的答案】
解:由(0.08+0.16+a+0.42+0.50+a+0.12+0.08+0.04)×0.5=1,
解得a=0.30.
因为前5组的频率之和为0.04+0.08+0.15+0.21+0.25=0.73>0.5.
而前4组的频率之和为0.04+0.08+0.15+0.21=0.48<0.5.
设中位数为x吨.
由0.50×(x-2)=0.5-0.48,解得x=2.04.
故可估计居民月均用水量的中位数为2.04吨.
【设计意图】加深对知识点的认识以及运用。
3.课堂小结
【预设的答案】
1.通过学习平均数、中位数和众数的计算级应用,重点培养数学运算素养及数据分析素养
2.一组数据中的众数可能不止一个,中位数是唯一的,求中位数时,必须先排序.
3.利用频率分布直方图求数字特征:
(1)众数是最高矩形的底边中点的横坐标.
(2)中位数左右两边直方图的面积应相等.
(3)平均数等于每个小矩形的面积乘以小矩形底边中点的横坐标之和.
四、课外作业
7
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
