专题:圆周运动重点题型归纳突破 (Word版含答案)
文档属性
| 名称 | 专题:圆周运动重点题型归纳突破 (Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 401.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-01-03 23:28:49 | ||
图片预览



文档简介
圆周运动重点题型归纳突破
一、圆周运动的概念
1.关于圆周运动下列说法正确的是( )
A.物体受一恒力作用,可能做匀速圆周运动 B.匀速圆周运动是变加速曲线运动
C.向心加速度描述的是线速度大小变化的快慢
D.做圆周运动(含变加速圆周运动)的物体,其加速度一定指向圆心
2.关于匀速圆周运动,下列说法正确的是( )
A.匀速圆周运动是匀变速曲线运动 B.匀速圆周运动是速度不变的运动
C.匀速圆周运动的加速度恒定不变 D.匀速圆周运动的角速度恒定不变
3.关于曲线运动的规律,下列说法中正确的是( )
A.匀速圆周运动是匀变速曲线运动 B.物体做曲线运动,其合力一定是变力
C.物体在恒力作用下不可能做曲线运动 D.做圆周运动的物体加速度不一定总指向圆心
4.下列说法正确的是( )
A.匀速圆周运动是匀速运动 B.平抛运动是匀加速运动
C.两个匀加速直线运动的合运动一定是直线运动 D.圆周运动的加速度一定指向圆心
二、描述圆周运动的几个物理量间的关系
5.如图所示为一皮带传动装置,右轮半径为r,a点在它的边缘上,左轮半径为2r,b点在它的边缘上。若在匀速转动过程中。皮带不打滑,则a、b两点( )
A.周期相等 B.角速度相等 C.线速度大小相等 D.都处于受力平衡状态
6.如图所示,摩天轮上有A、B两点,在摩天轮转动时,A、B两点的角速度大小分别为ωA、ωB,线速度大小分别为vA、vB,则( )
A.ωA>ωB,vA=vB B.ωA<ωB,vA=vB C.ωA=ωB,vAvB
7.如图为一皮带传动装置,a、b、c三点做圆周运动的半径之比ra︰rb︰rc=1︰2︰4。若a、b、c三点的线速度分别用υa、υb、υc表示,角速度分别用ωa、ωb、ωc表示,在传动过程中皮带不打滑,则下列关系式正确的是( )
A.υa︰υb︰υc=1︰2︰4 B.υa︰υb︰υc=4︰2︰1
C.ωa︰ωb︰ωc=2︰1︰1 D.ωa︰ωb︰ωc=1︰2︰2
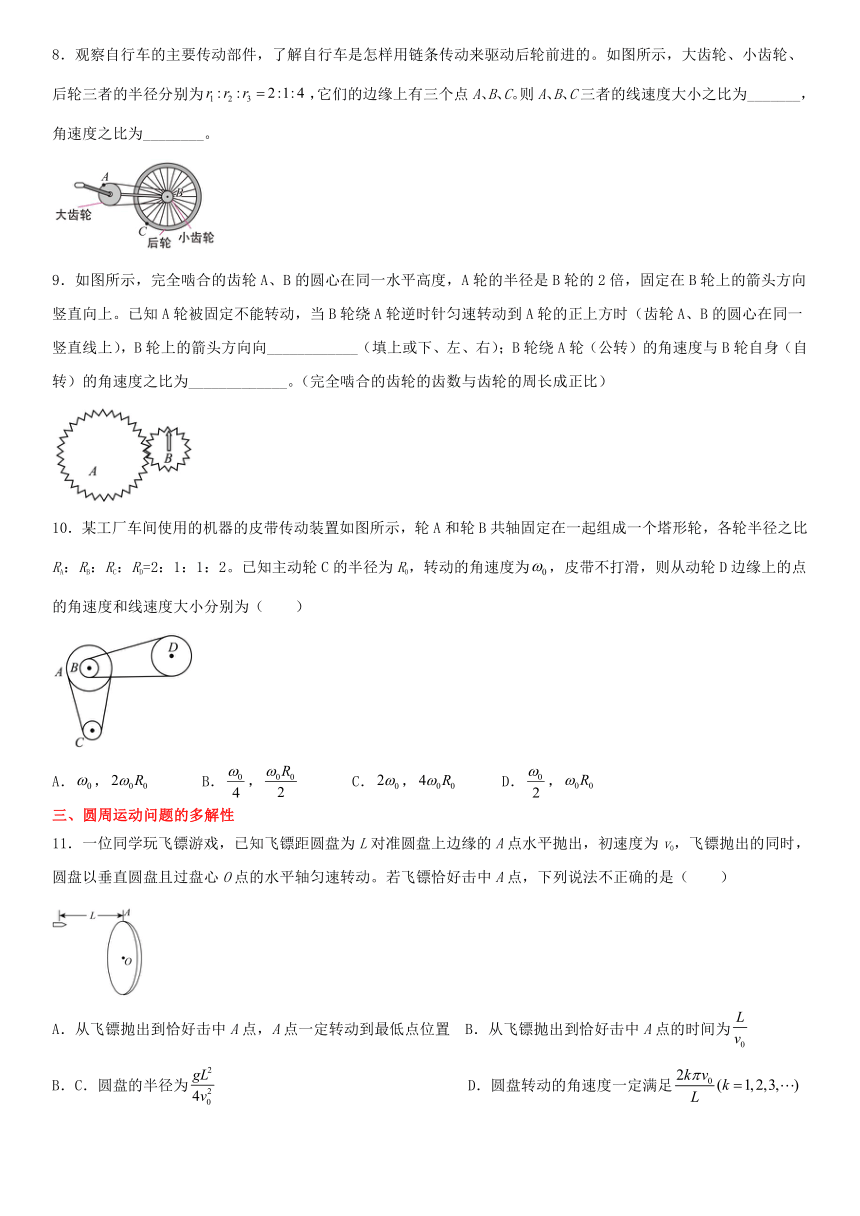
8.观察自行车的主要传动部件,了解自行车是怎样用链条传动来驱动后轮前进的。如图所示,大齿轮、小齿轮、后轮三者的半径分别为,它们的边缘上有三个点A、B、C。则A、B、C三者的线速度大小之比为_______,角速度之比为________。
9.如图所示,完全啮合的齿轮A、B的圆心在同一水平高度,A轮的半径是B轮的2倍,固定在B轮上的箭头方向竖直向上。已知A轮被固定不能转动,当B轮绕A轮逆时针匀速转动到A轮的正上方时(齿轮A、B的圆心在同一竖直线上),B轮上的箭头方向向____________(填上或下、左、右);B轮绕A轮(公转)的角速度与B轮自身(自转)的角速度之比为_____________。(完全啮合的齿轮的齿数与齿轮的周长成正比)
10.某工厂车间使用的机器的皮带传动装置如图所示,轮A和轮B共轴固定在一起组成一个塔形轮,各轮半径之比RA:RB:RC:RD=2:1:1:2。已知主动轮C的半径为R0,转动的角速度为,皮带不打滑,则从动轮D边缘上的点的角速度和线速度大小分别为( )
A., B., C., D.,
三、圆周运动问题的多解性
11.一位同学玩飞镖游戏,已知飞镖距圆盘为L对准圆盘上边缘的A点水平抛出,初速度为v0,飞镖抛出的同时,圆盘以垂直圆盘且过盘心O点的水平轴匀速转动。若飞镖恰好击中A点,下列说法不正确的是( )
从飞镖抛出到恰好击中A点,A点一定转动到最低点位置 B.从飞镖抛出到恰好击中A点的时间为
C.圆盘的半径为 D.圆盘转动的角速度一定满足
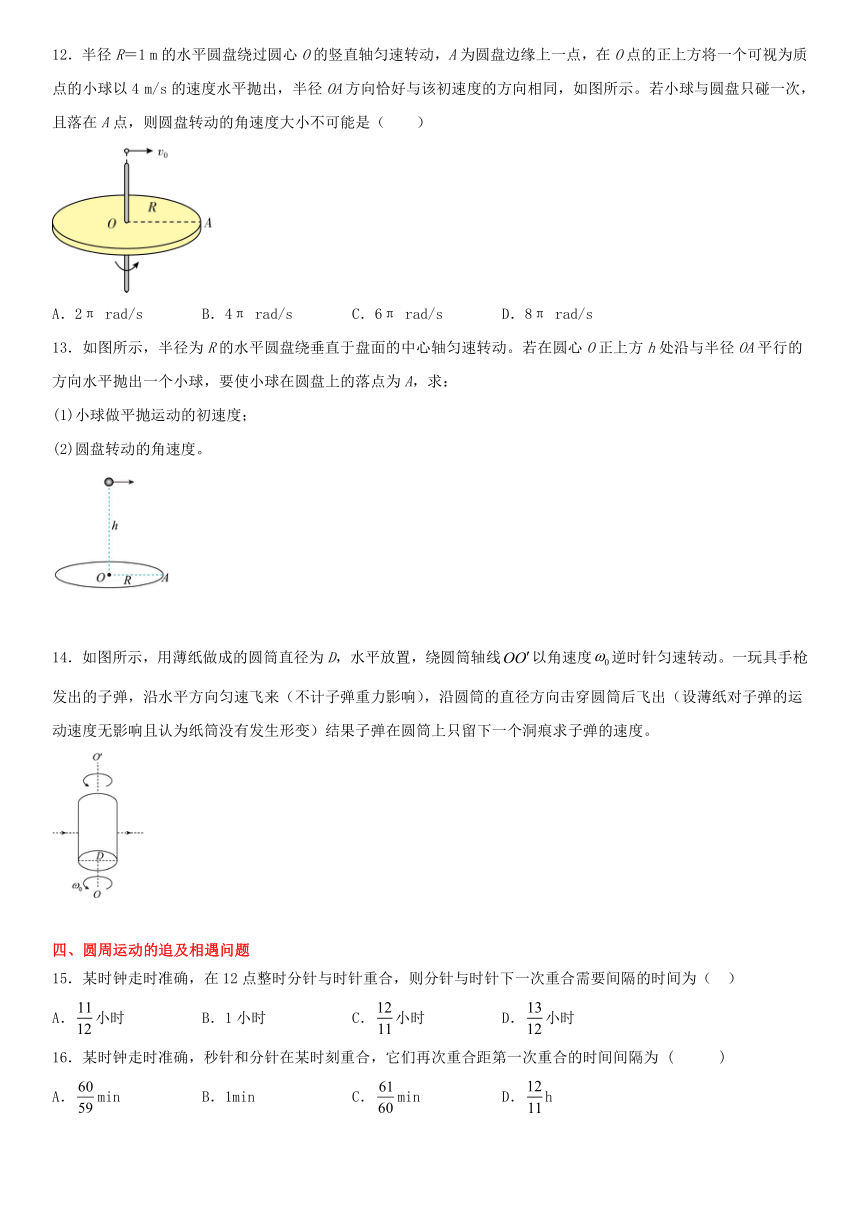
12.半径R=1 m的水平圆盘绕过圆心O的竖直轴匀速转动,A为圆盘边缘上一点,在O点的正上方将一个可视为质点的小球以4 m/s的速度水平抛出,半径OA方向恰好与该初速度的方向相同,如图所示。若小球与圆盘只碰一次,且落在A点,则圆盘转动的角速度大小不可能是( )
A.2π rad/s B.4π rad/s C.6π rad/s D.8π rad/s
13.如图所示,半径为R的水平圆盘绕垂直于盘面的中心轴匀速转动。若在圆心O正上方h处沿与半径OA平行的方向水平抛出一个小球,要使小球在圆盘上的落点为A,求:
(1)小球做平抛运动的初速度;
(2)圆盘转动的角速度。
14.如图所示,用薄纸做成的圆筒直径为D,水平放置,绕圆筒轴线以角速度逆时针匀速转动。一玩具手枪发出的子弹,沿水平方向匀速飞来(不计子弹重力影响),沿圆筒的直径方向击穿圆筒后飞出(设薄纸对子弹的运动速度无影响且认为纸筒没有发生形变)结果子弹在圆筒上只留下一个洞痕求子弹的速度。
四、圆周运动的追及相遇问题
15.某时钟走时准确,在12点整时分针与时针重合,则分针与时针下一次重合需要间隔的时间为( )
A.小时 B.1小时 C.小时 D.小时
16.某时钟走时准确,秒针和分针在某时刻重合,它们再次重合距第一次重合的时间间隔为 ( )
A.min B.1min C.min D.h
17.如图所示,质点a、b在同一平面内绕质点c沿逆时针方向做匀速圆周运动,它们的周期分别是Ta和Tb,
(1)试求出a、b距离最近的最短时间间隔;
(2)知Ta∶Tb=1∶k(k>1,为正整数)。试求出从图示位置开始,在b运动一周的过程中,a、b距离最近的次数。(结果用k表示)
18.如图所示,有A、B两质点绕同一点O做匀速圆周运动,运动方向相同,且此时A、B运动到图示位置。A的周期为,B的周期为,且,求:两质点下一次相遇所用的时间和第一次相距最远所用的时间。
答案
1.B
【详解】
A.由于合力F是恒力,而匀速圆周运动中合力提供向心力,方向不断改变,是变力,故物体不可能做匀速圆周运动,A错误;
B.匀速圆周运动的加速度始终指向圆心,方向时刻在变化,故加速度是变化的,所以是变加速曲线运动,B正确;
C.向心加速度只改变物体的速度的方向不改变速度的大小,所以向心加速度越大小,表示物体速度方向变化快慢,C错误;
D.做变加速圆周运动的物体,其速度的大小和方向都变化,所以其合力不指向圆心,其加速度不指向圆心,D错误。
故选B。
2.D
【详解】
ABC.匀速圆周运动的加速度与速度的方向时刻改变,所以是非匀变曲线运动,ABC错误;
D.匀速圆周运动的角速度恒定不变,D正确。
故选D。
3.D
【详解】
A.匀速圆周运动的加速度方向时刻变化,所以不是匀变速曲线运动,A错误;
BC.物体做曲线运动,其合力不一定是变力,如平抛运动,其合力是恒力,BC错误;
D.做匀速圆周运动的物体加速度一定总指向圆心,如果速率变化的圆周运动,其加速度不一定总指向圆心,D正确。
故选D。
4.B
【详解】
A.匀速圆周运动速度大小不变,方向变化,是变速运动,故A错误;
B.平抛运动在水平方向上做匀速直线运动,在竖直方向做自由落体运动,是两个直线运动的合运动.故B正确;
C.两个匀加速直线运动的合运动,若合加速度和合初速度方向不共线,则合运动是曲线运动,故C错误;
D.做变速圆周运动的物体,向心力指向圆心,但是在切线方向上有合力,最终的合力不指向圆心,则加速度也不指向圆心,故D错误。
故选B。
5.C
【详解】
A.本题为皮带传送装置,皮带传送装置中,皮带上的两点线速度相同,根据,且raB.皮带传送装置中,皮带上的两点线速度相同,根据,且raC.皮带传送装置中,皮带上的两点线速度相同,故va=vb,故C正确;
D.匀速转动过程过程中,a、b均做匀速圆周运动,匀速圆周运动不是匀速运动,故受力不平衡,故D错误。
故选:C。
6.D
【详解】
摩天轮上的A、B两点属于同轴转动,角速度相等,故
ωA=ωB
由于rBv=rω
可知
vA>vB
故选D。
7.C
【详解】
如图所示,a与b同一皮带下传动,则
va=vb
因为
ra:rb=1:2
根据v=ωr,所以
ωa:ωb=rb:ra=2:1
bc两点共轴,则
ωc=ωb
得角速度之比
ωa:ωb:ωc=2:1:1
因为
rc:rb=2:1
所以
vb:vc=1:2
即
va:vb:vc=1:1:2
故选C。
8.1:1:4 1:2:2
【详解】
[1][2]大齿轮与小齿轮是链条传动,边缘点线速度相等,则有
vA:vB=1:1
小齿轮与后轮是同轴传动,角速度相等,故
ωB:ωC=1:1
根据线速度与角速度关系公式
v=ωr
有
故
vA:vB:vC=1:1:4
ωA:ωB:ωC=1:2:2
9.右
【详解】
[1]当A被固定时只有B转动,则B以A的圆心为圆心进行转动,假设A的齿轮半径为2r,则B转动的半径为3r,当B转到A轮的正上方时,经过的路程为
则B自传的圆心角为
所以箭头朝右。
[2]公转角速度与自传角速度之比为
10.B
【详解】
C与A的线速度相同,可得
则A的角速度为
A和B是同轴,所以角速度相等,所以则有
又因为
所以
所以ACD错误,B正确。
故选B。
11.D
【详解】
A.飞镖抛出后做平抛运动,则飞镖抛出到恰好击中A点,A点一定转动到了圆盘最低点位置,故A正确;
B.飞镖水平抛出,在水平方向做匀速直线运动,因此
故B正确;
C.飞镖击中A点时,A恰好在最下方,有
解得
故C正确;
D.飞镖击中A点,则A点转过的角度满足
θ=ωt=π+2kπ(k=0、1、2......)
故
(k=0、1、2......)
故D错误。
本题选错误的,故选D。
12.ABC
【详解】
小球平抛运动的时间
小球平抛运动的时间和圆盘转动的时间相等,则有
解得
当时,,当时,,随着增大,增大,故ABC不可能,D可能。
故选ABC。
13.(1) ;(2)
【详解】
(1) 要使小球直接落在B点,水平位移要为R,对平抛的小球:水平方向:
,
联立得:
(2) 要使小球落到A处,则小球在下落的这段时间内,A点刚好转了n圈则:
ωt=2nπ (n=0、1、2…)
联立得:
14.()
【详解】
由于子弹在圆筒上只留下了一个洞痕,考虑匀速圆周运动的周期性,故有
解得
所以
15.C
【详解】
分针的周期为1小时,而时针的周期为12个小时,所以周期之比为:1:12,当下次相遇时,分针比时针多跑了一圈,故 ,所以 ,故C 正确;
故选C
16.A
【详解】
分针的周期为,秒针的周期为,两者的周期比为,分针与秒针从第1次重合到第2次重合有:,即,得时间间隔为,A正确.
17.(1);(2)k-1
【详解】
(1)设每隔时间T,a、b相距最近,则
(ωa-ωb)T=2π
所以
(2)故b运动一周的过程中,a、b相距最近的次数为
18.;
【详解】
由题设情境分析可知:A、B两质点下一次相遇的条件为
故
两质点第一次相距最远的条件为
解得
一、圆周运动的概念
1.关于圆周运动下列说法正确的是( )
A.物体受一恒力作用,可能做匀速圆周运动 B.匀速圆周运动是变加速曲线运动
C.向心加速度描述的是线速度大小变化的快慢
D.做圆周运动(含变加速圆周运动)的物体,其加速度一定指向圆心
2.关于匀速圆周运动,下列说法正确的是( )
A.匀速圆周运动是匀变速曲线运动 B.匀速圆周运动是速度不变的运动
C.匀速圆周运动的加速度恒定不变 D.匀速圆周运动的角速度恒定不变
3.关于曲线运动的规律,下列说法中正确的是( )
A.匀速圆周运动是匀变速曲线运动 B.物体做曲线运动,其合力一定是变力
C.物体在恒力作用下不可能做曲线运动 D.做圆周运动的物体加速度不一定总指向圆心
4.下列说法正确的是( )
A.匀速圆周运动是匀速运动 B.平抛运动是匀加速运动
C.两个匀加速直线运动的合运动一定是直线运动 D.圆周运动的加速度一定指向圆心
二、描述圆周运动的几个物理量间的关系
5.如图所示为一皮带传动装置,右轮半径为r,a点在它的边缘上,左轮半径为2r,b点在它的边缘上。若在匀速转动过程中。皮带不打滑,则a、b两点( )
A.周期相等 B.角速度相等 C.线速度大小相等 D.都处于受力平衡状态
6.如图所示,摩天轮上有A、B两点,在摩天轮转动时,A、B两点的角速度大小分别为ωA、ωB,线速度大小分别为vA、vB,则( )
A.ωA>ωB,vA=vB B.ωA<ωB,vA=vB C.ωA=ωB,vA
7.如图为一皮带传动装置,a、b、c三点做圆周运动的半径之比ra︰rb︰rc=1︰2︰4。若a、b、c三点的线速度分别用υa、υb、υc表示,角速度分别用ωa、ωb、ωc表示,在传动过程中皮带不打滑,则下列关系式正确的是( )
A.υa︰υb︰υc=1︰2︰4 B.υa︰υb︰υc=4︰2︰1
C.ωa︰ωb︰ωc=2︰1︰1 D.ωa︰ωb︰ωc=1︰2︰2
8.观察自行车的主要传动部件,了解自行车是怎样用链条传动来驱动后轮前进的。如图所示,大齿轮、小齿轮、后轮三者的半径分别为,它们的边缘上有三个点A、B、C。则A、B、C三者的线速度大小之比为_______,角速度之比为________。
9.如图所示,完全啮合的齿轮A、B的圆心在同一水平高度,A轮的半径是B轮的2倍,固定在B轮上的箭头方向竖直向上。已知A轮被固定不能转动,当B轮绕A轮逆时针匀速转动到A轮的正上方时(齿轮A、B的圆心在同一竖直线上),B轮上的箭头方向向____________(填上或下、左、右);B轮绕A轮(公转)的角速度与B轮自身(自转)的角速度之比为_____________。(完全啮合的齿轮的齿数与齿轮的周长成正比)
10.某工厂车间使用的机器的皮带传动装置如图所示,轮A和轮B共轴固定在一起组成一个塔形轮,各轮半径之比RA:RB:RC:RD=2:1:1:2。已知主动轮C的半径为R0,转动的角速度为,皮带不打滑,则从动轮D边缘上的点的角速度和线速度大小分别为( )
A., B., C., D.,
三、圆周运动问题的多解性
11.一位同学玩飞镖游戏,已知飞镖距圆盘为L对准圆盘上边缘的A点水平抛出,初速度为v0,飞镖抛出的同时,圆盘以垂直圆盘且过盘心O点的水平轴匀速转动。若飞镖恰好击中A点,下列说法不正确的是( )
从飞镖抛出到恰好击中A点,A点一定转动到最低点位置 B.从飞镖抛出到恰好击中A点的时间为
C.圆盘的半径为 D.圆盘转动的角速度一定满足
12.半径R=1 m的水平圆盘绕过圆心O的竖直轴匀速转动,A为圆盘边缘上一点,在O点的正上方将一个可视为质点的小球以4 m/s的速度水平抛出,半径OA方向恰好与该初速度的方向相同,如图所示。若小球与圆盘只碰一次,且落在A点,则圆盘转动的角速度大小不可能是( )
A.2π rad/s B.4π rad/s C.6π rad/s D.8π rad/s
13.如图所示,半径为R的水平圆盘绕垂直于盘面的中心轴匀速转动。若在圆心O正上方h处沿与半径OA平行的方向水平抛出一个小球,要使小球在圆盘上的落点为A,求:
(1)小球做平抛运动的初速度;
(2)圆盘转动的角速度。
14.如图所示,用薄纸做成的圆筒直径为D,水平放置,绕圆筒轴线以角速度逆时针匀速转动。一玩具手枪发出的子弹,沿水平方向匀速飞来(不计子弹重力影响),沿圆筒的直径方向击穿圆筒后飞出(设薄纸对子弹的运动速度无影响且认为纸筒没有发生形变)结果子弹在圆筒上只留下一个洞痕求子弹的速度。
四、圆周运动的追及相遇问题
15.某时钟走时准确,在12点整时分针与时针重合,则分针与时针下一次重合需要间隔的时间为( )
A.小时 B.1小时 C.小时 D.小时
16.某时钟走时准确,秒针和分针在某时刻重合,它们再次重合距第一次重合的时间间隔为 ( )
A.min B.1min C.min D.h
17.如图所示,质点a、b在同一平面内绕质点c沿逆时针方向做匀速圆周运动,它们的周期分别是Ta和Tb,
(1)试求出a、b距离最近的最短时间间隔;
(2)知Ta∶Tb=1∶k(k>1,为正整数)。试求出从图示位置开始,在b运动一周的过程中,a、b距离最近的次数。(结果用k表示)
18.如图所示,有A、B两质点绕同一点O做匀速圆周运动,运动方向相同,且此时A、B运动到图示位置。A的周期为,B的周期为,且,求:两质点下一次相遇所用的时间和第一次相距最远所用的时间。
答案
1.B
【详解】
A.由于合力F是恒力,而匀速圆周运动中合力提供向心力,方向不断改变,是变力,故物体不可能做匀速圆周运动,A错误;
B.匀速圆周运动的加速度始终指向圆心,方向时刻在变化,故加速度是变化的,所以是变加速曲线运动,B正确;
C.向心加速度只改变物体的速度的方向不改变速度的大小,所以向心加速度越大小,表示物体速度方向变化快慢,C错误;
D.做变加速圆周运动的物体,其速度的大小和方向都变化,所以其合力不指向圆心,其加速度不指向圆心,D错误。
故选B。
2.D
【详解】
ABC.匀速圆周运动的加速度与速度的方向时刻改变,所以是非匀变曲线运动,ABC错误;
D.匀速圆周运动的角速度恒定不变,D正确。
故选D。
3.D
【详解】
A.匀速圆周运动的加速度方向时刻变化,所以不是匀变速曲线运动,A错误;
BC.物体做曲线运动,其合力不一定是变力,如平抛运动,其合力是恒力,BC错误;
D.做匀速圆周运动的物体加速度一定总指向圆心,如果速率变化的圆周运动,其加速度不一定总指向圆心,D正确。
故选D。
4.B
【详解】
A.匀速圆周运动速度大小不变,方向变化,是变速运动,故A错误;
B.平抛运动在水平方向上做匀速直线运动,在竖直方向做自由落体运动,是两个直线运动的合运动.故B正确;
C.两个匀加速直线运动的合运动,若合加速度和合初速度方向不共线,则合运动是曲线运动,故C错误;
D.做变速圆周运动的物体,向心力指向圆心,但是在切线方向上有合力,最终的合力不指向圆心,则加速度也不指向圆心,故D错误。
故选B。
5.C
【详解】
A.本题为皮带传送装置,皮带传送装置中,皮带上的两点线速度相同,根据,且ra
D.匀速转动过程过程中,a、b均做匀速圆周运动,匀速圆周运动不是匀速运动,故受力不平衡,故D错误。
故选:C。
6.D
【详解】
摩天轮上的A、B两点属于同轴转动,角速度相等,故
ωA=ωB
由于rB
可知
vA>vB
故选D。
7.C
【详解】
如图所示,a与b同一皮带下传动,则
va=vb
因为
ra:rb=1:2
根据v=ωr,所以
ωa:ωb=rb:ra=2:1
bc两点共轴,则
ωc=ωb
得角速度之比
ωa:ωb:ωc=2:1:1
因为
rc:rb=2:1
所以
vb:vc=1:2
即
va:vb:vc=1:1:2
故选C。
8.1:1:4 1:2:2
【详解】
[1][2]大齿轮与小齿轮是链条传动,边缘点线速度相等,则有
vA:vB=1:1
小齿轮与后轮是同轴传动,角速度相等,故
ωB:ωC=1:1
根据线速度与角速度关系公式
v=ωr
有
故
vA:vB:vC=1:1:4
ωA:ωB:ωC=1:2:2
9.右
【详解】
[1]当A被固定时只有B转动,则B以A的圆心为圆心进行转动,假设A的齿轮半径为2r,则B转动的半径为3r,当B转到A轮的正上方时,经过的路程为
则B自传的圆心角为
所以箭头朝右。
[2]公转角速度与自传角速度之比为
10.B
【详解】
C与A的线速度相同,可得
则A的角速度为
A和B是同轴,所以角速度相等,所以则有
又因为
所以
所以ACD错误,B正确。
故选B。
11.D
【详解】
A.飞镖抛出后做平抛运动,则飞镖抛出到恰好击中A点,A点一定转动到了圆盘最低点位置,故A正确;
B.飞镖水平抛出,在水平方向做匀速直线运动,因此
故B正确;
C.飞镖击中A点时,A恰好在最下方,有
解得
故C正确;
D.飞镖击中A点,则A点转过的角度满足
θ=ωt=π+2kπ(k=0、1、2......)
故
(k=0、1、2......)
故D错误。
本题选错误的,故选D。
12.ABC
【详解】
小球平抛运动的时间
小球平抛运动的时间和圆盘转动的时间相等,则有
解得
当时,,当时,,随着增大,增大,故ABC不可能,D可能。
故选ABC。
13.(1) ;(2)
【详解】
(1) 要使小球直接落在B点,水平位移要为R,对平抛的小球:水平方向:
,
联立得:
(2) 要使小球落到A处,则小球在下落的这段时间内,A点刚好转了n圈则:
ωt=2nπ (n=0、1、2…)
联立得:
14.()
【详解】
由于子弹在圆筒上只留下了一个洞痕,考虑匀速圆周运动的周期性,故有
解得
所以
15.C
【详解】
分针的周期为1小时,而时针的周期为12个小时,所以周期之比为:1:12,当下次相遇时,分针比时针多跑了一圈,故 ,所以 ,故C 正确;
故选C
16.A
【详解】
分针的周期为,秒针的周期为,两者的周期比为,分针与秒针从第1次重合到第2次重合有:,即,得时间间隔为,A正确.
17.(1);(2)k-1
【详解】
(1)设每隔时间T,a、b相距最近,则
(ωa-ωb)T=2π
所以
(2)故b运动一周的过程中,a、b相距最近的次数为
18.;
【详解】
由题设情境分析可知:A、B两质点下一次相遇的条件为
故
两质点第一次相距最远的条件为
解得
