7.3.2正弦型函数的性质与图像同步训练-2021-2022学年高一上学期数学人教B版(2019)必修第三册(含答案)
文档属性
| 名称 | 7.3.2正弦型函数的性质与图像同步训练-2021-2022学年高一上学期数学人教B版(2019)必修第三册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 195.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-04 11:03:24 | ||
图片预览



文档简介
课时训练 正弦型函数的性质与图像
一、选择题
1.电流I(A)随时间t(s)变化的关系是I=2sin 100πt,t∈(0,+∞),则电流I变化的周期是( )
A. B.100 C. D.50
2.(2021·北京高一检测)已知函数f(x)=A sin (ωx+φ)的图像(部分)如图所示,则f(x)的解析式是( )
A.f(x)=5sin
B.f(x)=5sin
C.f(x)=5sin
D.f(x)=5sin
3. 函数y=A sin (ωx+φ)+b在一个周期内的图像如图(其中A>0,ω>0,<),则函数的解析式为( )
A.y=2sin +1
B.y=2sin +1
C.y=2sin +1
D.y=2sin +1
4.(2021·天水高一检测)若函数f(x)=A sin (φx+φ)(A>0,ω>0,0<φ<π)的部分图像如图所示,则函数f(x)图像的一条对称轴是( )
A.x=- B.x=-
C.x= D.
5.(2021·西安高一检测)已知函数f(x)=A sin (ωx+φ)(A>0,ω>0,0<φ<π)的部分图像如图所示,其中图像最高点和最低点的横坐标分别为和,图像在y轴上的截距为,则f=( )
A.1 B. C. D.0
6.已知函数f=2sin ωx(其中ω>0),若对任意x1∈,存在x2∈,使得f=f,则ω的取值范围为( )
A.ω≥3 B.0<ω≤3
C.0<ω≤ D.ω≥
7.已知函数f(x)=A sin (ωx+φ)(A>0,ω>0,0<φ<π)的部分图像如图所示,给出下列四个结论:
①f(x)的最小正周期为;
②f(x)的最小值为-4;
③是f(x)的一个对称中心;
④函数f(x)在区间上递增.
其中正确结论的个数是( )
A.4 B.3 C.2 D.1
8. 已知函数f=sin (ω>0)满足f=f=-, 且f在(x0,x0+1)上有最小值,无最大值.给出下述四个结论:
①f=-1;
②若x0=0,则f=sin ;
③f的最小正周期为3;
④f在上的零点个数最少为1 346个.
其中正确的结论是( )
A.①②④ B.①③④
C.①③ D.②④
9.矗立于伦敦泰晤士河畔的伦敦眼(The London Eye)是世界上首座,也曾经是世界最大的观景摩天轮,已知其旋转半径60 m,最高点距地面135 m,运行一周大约30分钟,某游客在最低点的位置坐上摩天轮,则第10分钟时他距地面大约为( )
A.95 m B.100 m
C.105 m D.110 m
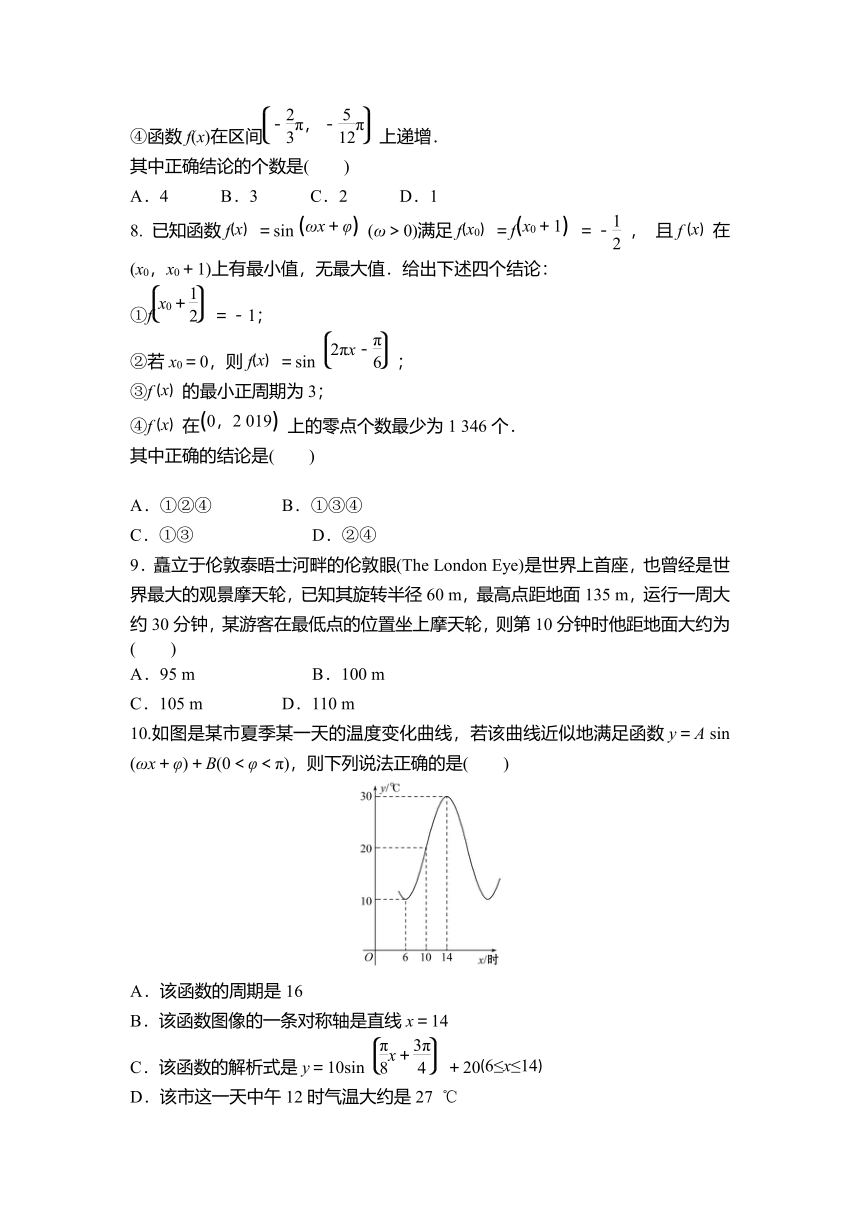
10.如图是某市夏季某一天的温度变化曲线,若该曲线近似地满足函数y=A sin (ωx+φ)+B(0<φ<π),则下列说法正确的是( )
A.该函数的周期是16
B.该函数图像的一条对称轴是直线x=14
C.该函数的解析式是y=10sin +20
D.该市这一天中午12时气温大约是27 ℃
11.(2021·莆田高一检测)若函数f(x)=A sin (ωx+φ)的部分图像,如图所示,则下列说法正确的是( )
A.φ=
B.函数f(x)的图像关于x=对称
C.函数f(x)的图像关于点对称
D.x∈时f(x)的值域为[-2,1]
13. 如图函数f(x)=A sin (ωx+φ)与坐标轴的三个交点P,Q,R满足P(2,0),∠PQR=,M为QR的中点,PM=2,则A的值为( )
A. B. C.8 D.16
二、填空题
14.已知函数f(x)=2sin ,若对任意x∈R都有f(x1)≤f(x)≤f(x2)(x1,x2∈R)成立,则|x1-x2|的最小值为________.
15.已知函数f(x)=A sin (ωx+φ)(A>0,ω>0,<)的图像与y轴的交点为,它在y轴右侧的第一个最高点和第一个最低点的坐标分别为和(x0+2π,-2).则φ=______,x0=________.
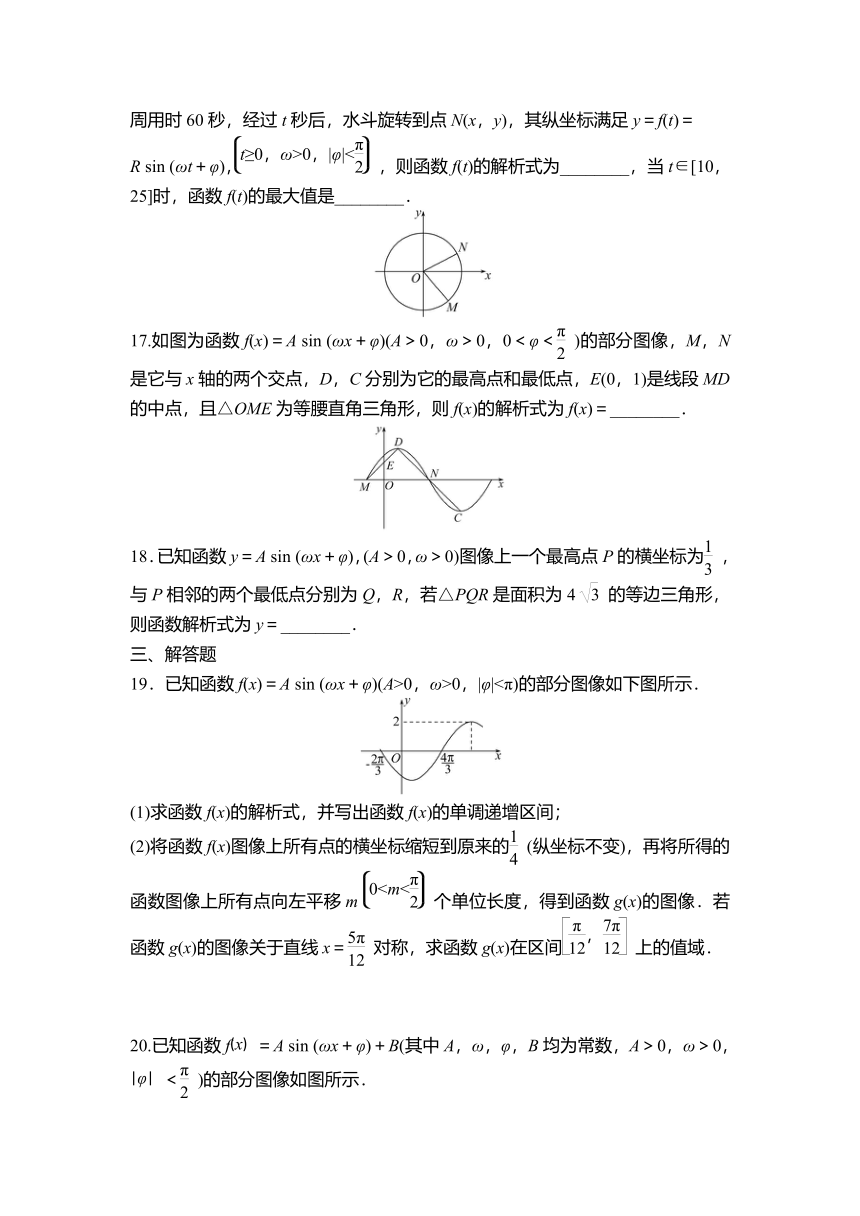
16.(2021·重庆高一检测)水车在古代是进行灌溉引水的工具,是人类的一项古老的发明,也是人类利用自然和改造自然的象征,如图是一个半径为R的水车,一个水斗从点M(2,-2)出发,沿圆周按逆时针方向匀速旋转,且旋转一周用时60秒,经过t秒后,水斗旋转到点N(x,y),其纵坐标满足y=f(t)=
R sin (ωt+φ),,则函数f(t)的解析式为________,当t∈[10,25]时,函数f(t)的最大值是________.
17.如图为函数f(x)=A sin (ωx+φ)(A>0,ω>0,0<φ<)的部分图像,M,N是它与x轴的两个交点,D,C分别为它的最高点和最低点,E(0,1)是线段MD的中点,且△OME为等腰直角三角形,则f(x)的解析式为f(x)=________.
18.已知函数y=A sin (ωx+φ),(A>0,ω>0)图像上一个最高点P的横坐标为,与P相邻的两个最低点分别为Q,R,若△PQR是面积为4的等边三角形,则函数解析式为y=________.
三、解答题
19.已知函数f(x)=A sin (ωx+φ)(A>0,ω>0,|φ|<π)的部分图像如下图所示.
(1)求函数f(x)的解析式,并写出函数f(x)的单调递增区间;
(2)将函数f(x)图像上所有点的横坐标缩短到原来的(纵坐标不变),再将所得的函数图像上所有点向左平移m个单位长度,得到函数g(x)的图像.若函数g(x)的图像关于直线x=对称,求函数g(x)在区间上的值域.
20.已知函数f=A sin (ωx+φ)+B(其中A,ω,φ,B均为常数,A>0,ω>0,<)的部分图像如图所示.
(1)求函数f的解析式;
(2)若先将函数f图像上所有点的横坐标变为原来的(纵坐标不变),再将图像向左平移m(m>0)个单位,得到函数g的图像,若g是奇函数,求实数m的最小值.
21.函数y=sin (ω>0,<)在同一个周期内,当x=时,y取最大值1,当x=时,y取最小值-1.
(1)求函数的解析式y=f(x);
(2)函数y=sin x的图像经过怎样的变换可得到y=f(x)的图像?
(3)若函数f(x)满足方程f(x)=a(0<a<1),求在[0,2π]内的所有实数根之和.
22.已知函数f=A sin (ωx+)(A>0,ω>0)只能同时满足下列三个条件中的两个:①函数f的最大值为2;②函数f的图像可由y=sin 的图像平移得到;③函数f图像的相邻两条对称轴之间的距离为.
(1)请写出这两个条件序号,并求出f的解析式;
(2)求方程f+1=0在区间上所有解的和.
参考答案
1.C
2.D
3. D
4.B
5. A
6.D
7.B
8. C
9. C
10. ABD
11.ABD
13. A
14.4π
15.
16.f(t)=4sin 4
17. 2sin
18.sin
19.【解析】(1)由图像可知A=2,
T=2=4π,
所以ω==,所以f(x)=2sin ,由图可求出最低点的坐标为,
所以f=2sin =-2,所以+φ=-+2kπ,所以φ=-+2kπ,k∈Z,
因为|φ|<π,所以φ=-,
所以f(x)=2sin ,
由-+2kπ≤x-≤+2kπ,k∈Z,可得+4kπ≤x≤+4kπ,k∈Z.
所以函数f(x)的单调递增区间为[+4kπ,+4kπ],k∈Z.
(2)由题意知,函数g(x)
=2sin =2sin ,
因为g(x)的图像关于直线x=对称,所以2×-+2m=+kπ,k∈Z,即m=+,k∈Z,因为0所以g(x)=2sin .
当x∈时,2x-∈,
可得sin ∈,
所以2sin ∈[-1,2],即函数g(x)的值域为[-1,2].
20. 【解析】(1)由图像可知A==1,
B==2,
=-=,所以T==π,
所以ω=2,所以f=sin +2.
由f=sin +2=1,
得+φ=2kπ+,k∈Z,
所以φ=2kπ-,k∈Z,
因为<,所以φ=-.
所以f=sin +2.
(2)由题意g=sin +2,
g=sin +2,
因为g是奇函数,所以4m-=kπ,k∈Z,
所以m=+,k∈Z,
因为m>0,所以当k=0时,m的最小值为.
21.【解析】(1)因为=2× ,所以ω=3,
又因为sin =1,所以+φ=2kπ+,
又|φ|<得φ=-,
所以函数f=sin ;
(2)y=sin x的图像向右平移个单位得
y=sin 的图像,
再由y=sin 图像上所有点的横坐标变为原来的,纵坐标不变,
得到y=sin 的图像;
(3)因为f(x)=sin 的周期为π,
所以y=sin 在[0,2π]内恰有3个周期,
所以sin =a(0<a<1)在[0,2π]内有6个实数根且x1+x2=,
同理,x3+x4=π,x5+x6=π,
故所有实数根之和为++=.
22.【解析】(1)函数f=A sin 满足的条件为①③.
理由如下:由题意可知条件①②互相矛盾,
故③为函数f=A sin 满足的条件之一,由③可知,T=π,所以ω=2,故②不合题意,
所以函数f=A sin 满足的条件为①③;由①可知A=2,所以f=2sin ;
(2)因为f+1=0,所以sin =-,
所以2x+=-+2kπ或2x+=+2kπ,
所以x=-+kπ或x=+kπ,
又因为x∈,
所以x的取值为-,,-,,
所以方程f+1=0在区间上所有解的和为.
一、选择题
1.电流I(A)随时间t(s)变化的关系是I=2sin 100πt,t∈(0,+∞),则电流I变化的周期是( )
A. B.100 C. D.50
2.(2021·北京高一检测)已知函数f(x)=A sin (ωx+φ)的图像(部分)如图所示,则f(x)的解析式是( )
A.f(x)=5sin
B.f(x)=5sin
C.f(x)=5sin
D.f(x)=5sin
3. 函数y=A sin (ωx+φ)+b在一个周期内的图像如图(其中A>0,ω>0,<),则函数的解析式为( )
A.y=2sin +1
B.y=2sin +1
C.y=2sin +1
D.y=2sin +1
4.(2021·天水高一检测)若函数f(x)=A sin (φx+φ)(A>0,ω>0,0<φ<π)的部分图像如图所示,则函数f(x)图像的一条对称轴是( )
A.x=- B.x=-
C.x= D.
5.(2021·西安高一检测)已知函数f(x)=A sin (ωx+φ)(A>0,ω>0,0<φ<π)的部分图像如图所示,其中图像最高点和最低点的横坐标分别为和,图像在y轴上的截距为,则f=( )
A.1 B. C. D.0
6.已知函数f=2sin ωx(其中ω>0),若对任意x1∈,存在x2∈,使得f=f,则ω的取值范围为( )
A.ω≥3 B.0<ω≤3
C.0<ω≤ D.ω≥
7.已知函数f(x)=A sin (ωx+φ)(A>0,ω>0,0<φ<π)的部分图像如图所示,给出下列四个结论:
①f(x)的最小正周期为;
②f(x)的最小值为-4;
③是f(x)的一个对称中心;
④函数f(x)在区间上递增.
其中正确结论的个数是( )
A.4 B.3 C.2 D.1
8. 已知函数f=sin (ω>0)满足f=f=-, 且f在(x0,x0+1)上有最小值,无最大值.给出下述四个结论:
①f=-1;
②若x0=0,则f=sin ;
③f的最小正周期为3;
④f在上的零点个数最少为1 346个.
其中正确的结论是( )
A.①②④ B.①③④
C.①③ D.②④
9.矗立于伦敦泰晤士河畔的伦敦眼(The London Eye)是世界上首座,也曾经是世界最大的观景摩天轮,已知其旋转半径60 m,最高点距地面135 m,运行一周大约30分钟,某游客在最低点的位置坐上摩天轮,则第10分钟时他距地面大约为( )
A.95 m B.100 m
C.105 m D.110 m
10.如图是某市夏季某一天的温度变化曲线,若该曲线近似地满足函数y=A sin (ωx+φ)+B(0<φ<π),则下列说法正确的是( )
A.该函数的周期是16
B.该函数图像的一条对称轴是直线x=14
C.该函数的解析式是y=10sin +20
D.该市这一天中午12时气温大约是27 ℃
11.(2021·莆田高一检测)若函数f(x)=A sin (ωx+φ)的部分图像,如图所示,则下列说法正确的是( )
A.φ=
B.函数f(x)的图像关于x=对称
C.函数f(x)的图像关于点对称
D.x∈时f(x)的值域为[-2,1]
13. 如图函数f(x)=A sin (ωx+φ)与坐标轴的三个交点P,Q,R满足P(2,0),∠PQR=,M为QR的中点,PM=2,则A的值为( )
A. B. C.8 D.16
二、填空题
14.已知函数f(x)=2sin ,若对任意x∈R都有f(x1)≤f(x)≤f(x2)(x1,x2∈R)成立,则|x1-x2|的最小值为________.
15.已知函数f(x)=A sin (ωx+φ)(A>0,ω>0,<)的图像与y轴的交点为,它在y轴右侧的第一个最高点和第一个最低点的坐标分别为和(x0+2π,-2).则φ=______,x0=________.
16.(2021·重庆高一检测)水车在古代是进行灌溉引水的工具,是人类的一项古老的发明,也是人类利用自然和改造自然的象征,如图是一个半径为R的水车,一个水斗从点M(2,-2)出发,沿圆周按逆时针方向匀速旋转,且旋转一周用时60秒,经过t秒后,水斗旋转到点N(x,y),其纵坐标满足y=f(t)=
R sin (ωt+φ),,则函数f(t)的解析式为________,当t∈[10,25]时,函数f(t)的最大值是________.
17.如图为函数f(x)=A sin (ωx+φ)(A>0,ω>0,0<φ<)的部分图像,M,N是它与x轴的两个交点,D,C分别为它的最高点和最低点,E(0,1)是线段MD的中点,且△OME为等腰直角三角形,则f(x)的解析式为f(x)=________.
18.已知函数y=A sin (ωx+φ),(A>0,ω>0)图像上一个最高点P的横坐标为,与P相邻的两个最低点分别为Q,R,若△PQR是面积为4的等边三角形,则函数解析式为y=________.
三、解答题
19.已知函数f(x)=A sin (ωx+φ)(A>0,ω>0,|φ|<π)的部分图像如下图所示.
(1)求函数f(x)的解析式,并写出函数f(x)的单调递增区间;
(2)将函数f(x)图像上所有点的横坐标缩短到原来的(纵坐标不变),再将所得的函数图像上所有点向左平移m个单位长度,得到函数g(x)的图像.若函数g(x)的图像关于直线x=对称,求函数g(x)在区间上的值域.
20.已知函数f=A sin (ωx+φ)+B(其中A,ω,φ,B均为常数,A>0,ω>0,<)的部分图像如图所示.
(1)求函数f的解析式;
(2)若先将函数f图像上所有点的横坐标变为原来的(纵坐标不变),再将图像向左平移m(m>0)个单位,得到函数g的图像,若g是奇函数,求实数m的最小值.
21.函数y=sin (ω>0,<)在同一个周期内,当x=时,y取最大值1,当x=时,y取最小值-1.
(1)求函数的解析式y=f(x);
(2)函数y=sin x的图像经过怎样的变换可得到y=f(x)的图像?
(3)若函数f(x)满足方程f(x)=a(0<a<1),求在[0,2π]内的所有实数根之和.
22.已知函数f=A sin (ωx+)(A>0,ω>0)只能同时满足下列三个条件中的两个:①函数f的最大值为2;②函数f的图像可由y=sin 的图像平移得到;③函数f图像的相邻两条对称轴之间的距离为.
(1)请写出这两个条件序号,并求出f的解析式;
(2)求方程f+1=0在区间上所有解的和.
参考答案
1.C
2.D
3. D
4.B
5. A
6.D
7.B
8. C
9. C
10. ABD
11.ABD
13. A
14.4π
15.
16.f(t)=4sin 4
17. 2sin
18.sin
19.【解析】(1)由图像可知A=2,
T=2=4π,
所以ω==,所以f(x)=2sin ,由图可求出最低点的坐标为,
所以f=2sin =-2,所以+φ=-+2kπ,所以φ=-+2kπ,k∈Z,
因为|φ|<π,所以φ=-,
所以f(x)=2sin ,
由-+2kπ≤x-≤+2kπ,k∈Z,可得+4kπ≤x≤+4kπ,k∈Z.
所以函数f(x)的单调递增区间为[+4kπ,+4kπ],k∈Z.
(2)由题意知,函数g(x)
=2sin =2sin ,
因为g(x)的图像关于直线x=对称,所以2×-+2m=+kπ,k∈Z,即m=+,k∈Z,因为0
当x∈时,2x-∈,
可得sin ∈,
所以2sin ∈[-1,2],即函数g(x)的值域为[-1,2].
20. 【解析】(1)由图像可知A==1,
B==2,
=-=,所以T==π,
所以ω=2,所以f=sin +2.
由f=sin +2=1,
得+φ=2kπ+,k∈Z,
所以φ=2kπ-,k∈Z,
因为<,所以φ=-.
所以f=sin +2.
(2)由题意g=sin +2,
g=sin +2,
因为g是奇函数,所以4m-=kπ,k∈Z,
所以m=+,k∈Z,
因为m>0,所以当k=0时,m的最小值为.
21.【解析】(1)因为=2× ,所以ω=3,
又因为sin =1,所以+φ=2kπ+,
又|φ|<得φ=-,
所以函数f=sin ;
(2)y=sin x的图像向右平移个单位得
y=sin 的图像,
再由y=sin 图像上所有点的横坐标变为原来的,纵坐标不变,
得到y=sin 的图像;
(3)因为f(x)=sin 的周期为π,
所以y=sin 在[0,2π]内恰有3个周期,
所以sin =a(0<a<1)在[0,2π]内有6个实数根且x1+x2=,
同理,x3+x4=π,x5+x6=π,
故所有实数根之和为++=.
22.【解析】(1)函数f=A sin 满足的条件为①③.
理由如下:由题意可知条件①②互相矛盾,
故③为函数f=A sin 满足的条件之一,由③可知,T=π,所以ω=2,故②不合题意,
所以函数f=A sin 满足的条件为①③;由①可知A=2,所以f=2sin ;
(2)因为f+1=0,所以sin =-,
所以2x+=-+2kπ或2x+=+2kπ,
所以x=-+kπ或x=+kπ,
又因为x∈,
所以x的取值为-,,-,,
所以方程f+1=0在区间上所有解的和为.
