三角形的中位线
图片预览
文档简介
建宁中学五步分层教学法学案
姓名:
班级:
课题:三角形的中位线
目
标
展
示
学习目标:经历三角形中位线的性质定理的形成过程,掌握定理,并能利用它们解决简单的问题。
重点难点:
重点:三角形的中位线性质。
难点:三角形的中位线性质的应用。
温
故
链
接
在△ABC 中,点D、E分别是BC、AC的中点,则AD、BE分别是 △ABC的 ,且分别能将△ABC分成 的两部分。
问
题
导
学
自主学习:
(1)三角形的中位线指的是 。如图:在
△ABC 中,点D、E分别是AB、AC的中点,则DE是△ABC的 。
(2)我们曾解决过如下的问题:在△ABC中,DE∥BC,则_____∽______,
由此可以进一步推知,当点D是AB的中点时,点E也是_______的中点。如果点D、E原来就是AB与AC的中点,那么是否可以推出DE∥BC呢? DE与BC之间存在什么样的数量关系呢?
合作探究:
猜想:三角形的中位线的性质定理 。
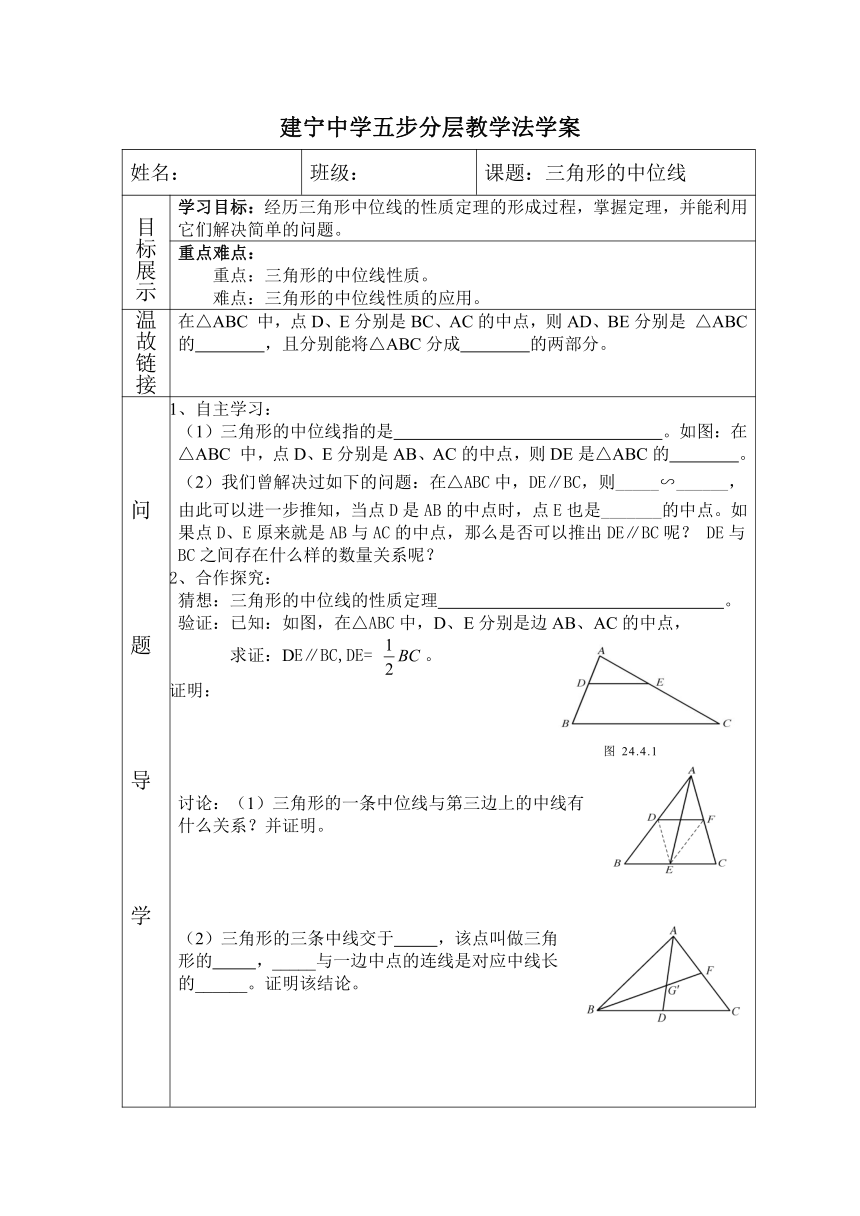
验证:已知:如图,在△ABC中,D、E分别是边AB、AC的中点,
求证:DE∥BC,DE= 。
证明:
讨论:(1)三角形的一条中位线与第三边上的中线有什么关系?并证明。
(2)三角形的三条中线交于 ,该点叫做三角形的 ,_____与一边中点的连线是对应中线长的______。证明该结论。
巩
固
训
练
基础达标:
(1)三角形的周长为56cm,则它的三条中位线组成的三角形的周长是__________cm。
(2)如图,在△ABC中,AB=AC,D、E、F分别是AB、BC、CA的中点.求证:四边形ADEF是菱形。
(3)如图,△ABC中,D、E、F分别为BC、AC、AB的中点,AD、BE、CF相交于点O,AB=6,BC=10,AC=8.试求出线段DE、OA、OF的长度与∠EDF的大小.
2、能力提升:
(1)如图,E、F、G、H分别是BD、BC、AC、AD的中点,且AB=DC,下列结论:①EFGH为矩形;②FH平分EG于T;③EG⊥FH;④HF平分∠EHG.其中正确的是( )A、①和② B、②和③ C、①②④ D、②③④
(2)如图,在△ABC中,D、E、F分别是各边的中点,AH是BC边上的高。
①试判断四边形DHEF是什么样的四边形,并证明;
②当AB、AC之间满足什么关系时,四边形DHCF是平行四边形?请证明;四边形DHCF能否为矩形或菱形?(直接写出结论.不要证明)
课后反思
本节课你的收获是: 。
你的疑点是: 。
姓名:
班级:
课题:三角形的中位线
目
标
展
示
学习目标:经历三角形中位线的性质定理的形成过程,掌握定理,并能利用它们解决简单的问题。
重点难点:
重点:三角形的中位线性质。
难点:三角形的中位线性质的应用。
温
故
链
接
在△ABC 中,点D、E分别是BC、AC的中点,则AD、BE分别是 △ABC的 ,且分别能将△ABC分成 的两部分。
问
题
导
学
自主学习:
(1)三角形的中位线指的是 。如图:在
△ABC 中,点D、E分别是AB、AC的中点,则DE是△ABC的 。
(2)我们曾解决过如下的问题:在△ABC中,DE∥BC,则_____∽______,
由此可以进一步推知,当点D是AB的中点时,点E也是_______的中点。如果点D、E原来就是AB与AC的中点,那么是否可以推出DE∥BC呢? DE与BC之间存在什么样的数量关系呢?
合作探究:
猜想:三角形的中位线的性质定理 。
验证:已知:如图,在△ABC中,D、E分别是边AB、AC的中点,
求证:DE∥BC,DE= 。
证明:
讨论:(1)三角形的一条中位线与第三边上的中线有什么关系?并证明。
(2)三角形的三条中线交于 ,该点叫做三角形的 ,_____与一边中点的连线是对应中线长的______。证明该结论。
巩
固
训
练
基础达标:
(1)三角形的周长为56cm,则它的三条中位线组成的三角形的周长是__________cm。
(2)如图,在△ABC中,AB=AC,D、E、F分别是AB、BC、CA的中点.求证:四边形ADEF是菱形。
(3)如图,△ABC中,D、E、F分别为BC、AC、AB的中点,AD、BE、CF相交于点O,AB=6,BC=10,AC=8.试求出线段DE、OA、OF的长度与∠EDF的大小.
2、能力提升:
(1)如图,E、F、G、H分别是BD、BC、AC、AD的中点,且AB=DC,下列结论:①EFGH为矩形;②FH平分EG于T;③EG⊥FH;④HF平分∠EHG.其中正确的是( )A、①和② B、②和③ C、①②④ D、②③④
(2)如图,在△ABC中,D、E、F分别是各边的中点,AH是BC边上的高。
①试判断四边形DHEF是什么样的四边形,并证明;
②当AB、AC之间满足什么关系时,四边形DHCF是平行四边形?请证明;四边形DHCF能否为矩形或菱形?(直接写出结论.不要证明)
课后反思
本节课你的收获是: 。
你的疑点是: 。
