2021-2022学年高二上学期数学人教B版(2019)选择性必修第一册2.3.1圆的标准方程课件(共19张PPT)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教B版(2019)选择性必修第一册2.3.1圆的标准方程课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-04 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
圆的标准方程
复习引入
问题1:平面直角坐标系中两点间的距离公式
问题2:什么是圆?初中我们是如何定义圆的?
问题3:确定圆需要几个要素?
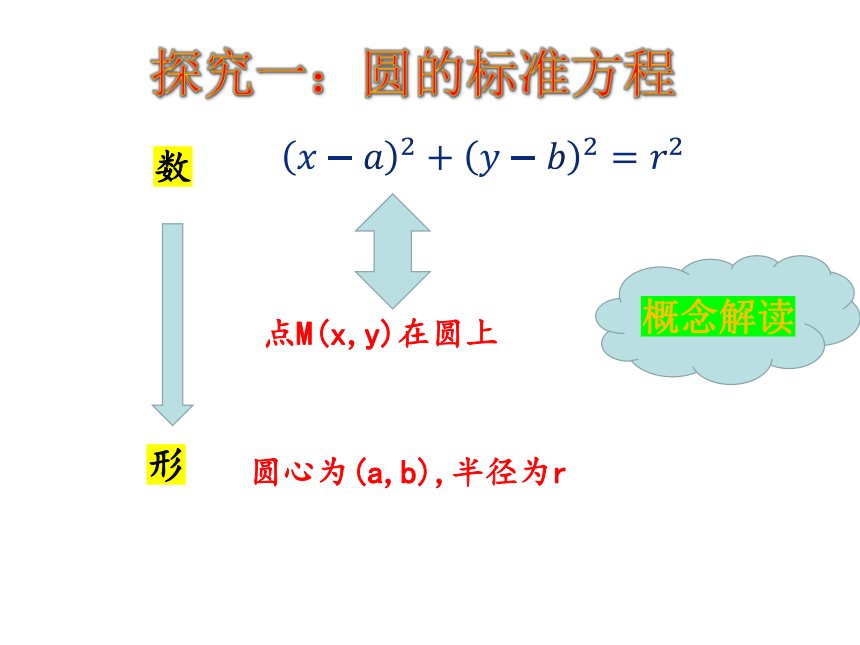
探究一:圆的标准方程
如图所示,设平面直角坐标系中的☉C的圆心坐标为C(1,2),且半径为2
(1)判断点A(3,2) 是否在圆☉C上;
(2)设M(x , y)是平面坐标系中任意一点,那么M在在☉C上的充要条件是什么?此时是x,y要满足什么关系式?
探究一:圆的标准方程
(3)设平面直角坐标系中的 C的圆心坐标为(a,b) ,半径为r(r>0) ; 设M(x , y)是平面坐标系中任意一点,那么M在☉C上的充要条件是什么?
探究一:圆的标准方程
分析:点 M(x , y)在 C上的充要条件|CM|=r,
即:
圆的标准方程
=r
即
探究一:圆的标准方程
概念解读
点M(x,y)在圆上
数
形
圆心为(a,b),半径为r
1.判断
(x-a)2+(y-b)2=m2一定表示圆的方程.( )
2.已知圆的标准方程,说出圆心和半径。
小试牛刀
探究一:圆的标准方程
小试牛刀
小试牛刀
探究一:圆的标准方程
思维拓展
一些特殊位置的圆的标准方程
1.圆心在原点
2.圆心在x轴上
3.圆心在y轴上
4.圆切于x轴
5.圆切于y轴
6.圆心在直线y=x上
a=b=0
b=0
a=0
r=|b|
r=|a|
a=b
探究二:求圆的标准方程
例1:根据下列条件,求圆的标准方程
(1)圆心在点C(-2,1),且过点A(2,-2);
直接法
已知圆心和半径
解:
所求圆的半径
又因为圆心为(-2,1),所以圆的方程为
探究二:求圆的标准方程
例1:(2)过点(0,1)和(2,1),半径为.
待定系数法
解:设圆的方程为
因为(0,1),(2,1)是圆上的点,
所以:
解得:
或
所以:圆的方程是
或
探究二:求圆的标准方程
待定系数法求圆的标准方程的一般步骤
探究二:求圆的标准方程
跟踪练习:
(1)以两点A(-3,-1)和B(5,5)为直径端点的圆的方程是
(2)与y轴相切,且圆心坐标为(-5,-3)的圆的标准方程为
探究二:求圆的标准方程
例2:求经过点P(1,1)和坐标原点,并且圆心在直线2x+3y+1=0
上的圆的标准方程.
解:方法一(待定系数法)
设圆的标准方程为(x-a)2+(y-b)2=r2
则:
解得
∴圆的标准方程是(x-4)2+(y+3)2=25.
探究二:求圆的标准方程
例2:求经过点P(1,1)和坐标原点,并且圆心在直线2x+3y+1=0
上的圆的标准方程.
解:方法二(几何法)
由题意知OP是圆的弦,其垂直平分线为x+y-1=0.
∵弦的垂直平分线过圆心,
解得
即圆心坐标为(4,-3),半径为r=5.
∴圆的标准方程是(x-4)2+(y+3)2=25.
由
探究二:求圆的标准方程
方法归纳
求圆的标准方程的方法:
1.直接法:已知圆心和半径
2.待定系数法:根据题设条件,列出方程组,解方程组得到所要的值,从而得出圆的标准方程。
3.几何法:根据确定圆的要素,几何性质以及题设条件,分别求出圆心和半径,进而得到圆的标准方程。
A
x
y
o
M1
M3
M2
如果设点M到圆心的距离为d,则可以看到:
点在圆内 d点在圆外 d > r .
点在圆上 d =r ;
探究三:点与圆的位置关系
探究三:点与圆的位置关系
圆的标准方程:
点在圆上:
点在圆内:
点在圆外:
探究三:点与圆的位置关系
小试牛刀
(1)判断A(1,1),B(1,2)和C(2,4)与圆的位置关系
(2)判断M(n,-5)与圆的位置关系
归纳总结
本节课你有什么收获?
(1)圆的标准方程
(2)求圆的标准方程的方法:
a.直接法
b.待定系数法
c.几何法
(3)点与圆的位置关系
圆的标准方程
复习引入
问题1:平面直角坐标系中两点间的距离公式
问题2:什么是圆?初中我们是如何定义圆的?
问题3:确定圆需要几个要素?
探究一:圆的标准方程
如图所示,设平面直角坐标系中的☉C的圆心坐标为C(1,2),且半径为2
(1)判断点A(3,2) 是否在圆☉C上;
(2)设M(x , y)是平面坐标系中任意一点,那么M在在☉C上的充要条件是什么?此时是x,y要满足什么关系式?
探究一:圆的标准方程
(3)设平面直角坐标系中的 C的圆心坐标为(a,b) ,半径为r(r>0) ; 设M(x , y)是平面坐标系中任意一点,那么M在☉C上的充要条件是什么?
探究一:圆的标准方程
分析:点 M(x , y)在 C上的充要条件|CM|=r,
即:
圆的标准方程
=r
即
探究一:圆的标准方程
概念解读
点M(x,y)在圆上
数
形
圆心为(a,b),半径为r
1.判断
(x-a)2+(y-b)2=m2一定表示圆的方程.( )
2.已知圆的标准方程,说出圆心和半径。
小试牛刀
探究一:圆的标准方程
小试牛刀
小试牛刀
探究一:圆的标准方程
思维拓展
一些特殊位置的圆的标准方程
1.圆心在原点
2.圆心在x轴上
3.圆心在y轴上
4.圆切于x轴
5.圆切于y轴
6.圆心在直线y=x上
a=b=0
b=0
a=0
r=|b|
r=|a|
a=b
探究二:求圆的标准方程
例1:根据下列条件,求圆的标准方程
(1)圆心在点C(-2,1),且过点A(2,-2);
直接法
已知圆心和半径
解:
所求圆的半径
又因为圆心为(-2,1),所以圆的方程为
探究二:求圆的标准方程
例1:(2)过点(0,1)和(2,1),半径为.
待定系数法
解:设圆的方程为
因为(0,1),(2,1)是圆上的点,
所以:
解得:
或
所以:圆的方程是
或
探究二:求圆的标准方程
待定系数法求圆的标准方程的一般步骤
探究二:求圆的标准方程
跟踪练习:
(1)以两点A(-3,-1)和B(5,5)为直径端点的圆的方程是
(2)与y轴相切,且圆心坐标为(-5,-3)的圆的标准方程为
探究二:求圆的标准方程
例2:求经过点P(1,1)和坐标原点,并且圆心在直线2x+3y+1=0
上的圆的标准方程.
解:方法一(待定系数法)
设圆的标准方程为(x-a)2+(y-b)2=r2
则:
解得
∴圆的标准方程是(x-4)2+(y+3)2=25.
探究二:求圆的标准方程
例2:求经过点P(1,1)和坐标原点,并且圆心在直线2x+3y+1=0
上的圆的标准方程.
解:方法二(几何法)
由题意知OP是圆的弦,其垂直平分线为x+y-1=0.
∵弦的垂直平分线过圆心,
解得
即圆心坐标为(4,-3),半径为r=5.
∴圆的标准方程是(x-4)2+(y+3)2=25.
由
探究二:求圆的标准方程
方法归纳
求圆的标准方程的方法:
1.直接法:已知圆心和半径
2.待定系数法:根据题设条件,列出方程组,解方程组得到所要的值,从而得出圆的标准方程。
3.几何法:根据确定圆的要素,几何性质以及题设条件,分别求出圆心和半径,进而得到圆的标准方程。
A
x
y
o
M1
M3
M2
如果设点M到圆心的距离为d,则可以看到:
点在圆内 d
点在圆上 d =r ;
探究三:点与圆的位置关系
探究三:点与圆的位置关系
圆的标准方程:
点在圆上:
点在圆内:
点在圆外:
探究三:点与圆的位置关系
小试牛刀
(1)判断A(1,1),B(1,2)和C(2,4)与圆的位置关系
(2)判断M(n,-5)与圆的位置关系
归纳总结
本节课你有什么收获?
(1)圆的标准方程
(2)求圆的标准方程的方法:
a.直接法
b.待定系数法
c.几何法
(3)点与圆的位置关系
