沪科版数学八年级上册 第13章 三角形中的边角关系、命题与证明 课件(共20张PPT)
文档属性
| 名称 | 沪科版数学八年级上册 第13章 三角形中的边角关系、命题与证明 课件(共20张PPT) | 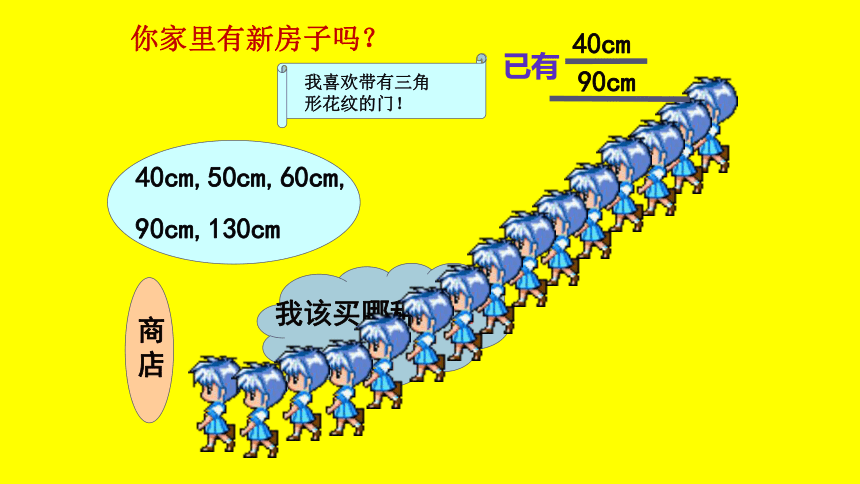 | |
| 格式 | pptx | ||
| 文件大小 | 417.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-05 16:31:04 | ||
图片预览





文档简介
(共20张PPT)
40cm,50cm,60cm,
90cm,130cm
我该买哪种呢?
40cm
90cm
已有
商店
你家里有新房子吗?
我喜欢带有三角形花纹的门!
三角形的三边关系
温故知新:
1、我们在小学都学过那些图形?
你能快速的画出这些图形吗?
2、通过自己的动手你认为在三角形、长方形、正方形、梯形这些图形中哪个图形最好画?
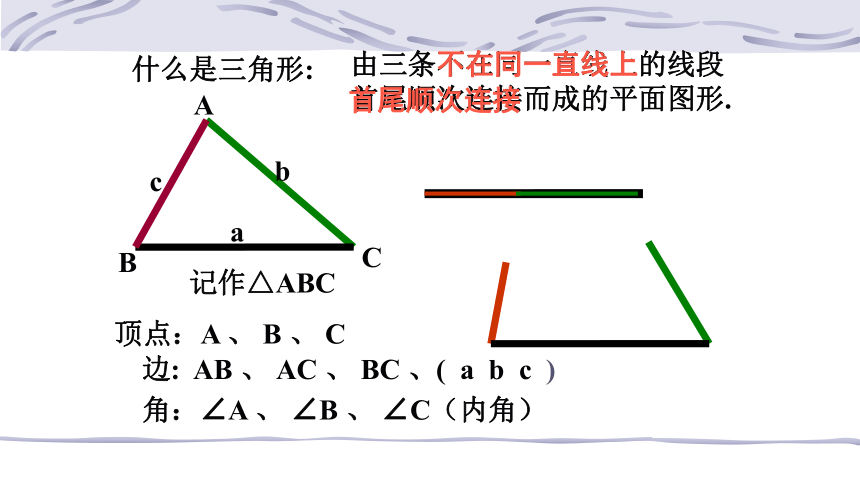
什么是三角形:
由三条不在同一直线上的线段首尾顺次连接而成的平面图形.
不在同一直线上
首尾顺次连接
A
B
C
记作△ABC
边: AB 、 AC 、 BC 、( a b c )
c
a
b
角:∠A 、 ∠B 、 ∠C(内角)
顶点:A 、 B 、 C
练一练
在下面自己画一个三角形用你喜欢的字母来表示它.
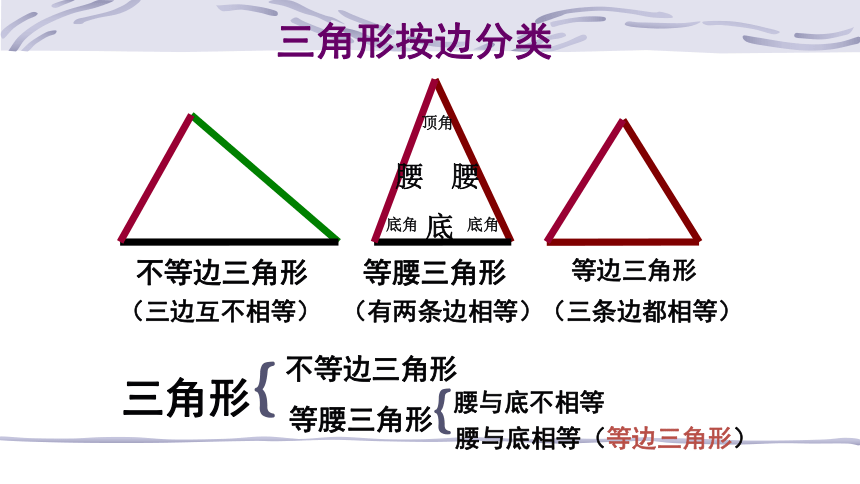
三角形按边分类
等腰三角形
(三边互不相等)
(有两条边相等)
(三条边都相等)
腰
腰
底
底角
底角
顶角
﹛
三角形
不等边三角形
﹛
腰与底不相等
腰与底相等(等边三角形)
不等边三角形
等腰三角形
等边三角形
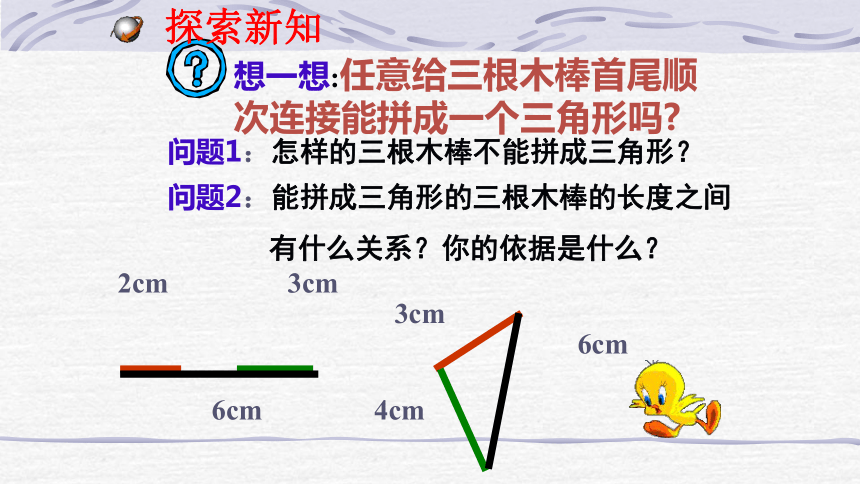
想一想:任意给三根木棒首尾顺次连接能拼成一个三角形吗
问题1:怎样的三根木棒不能拼成三角形?
问题2:能拼成三角形的三根木棒的长度之间
有什么关系?你的依据是什么?
探索新知
2cm
3cm
6cm
3cm
4cm
6cm
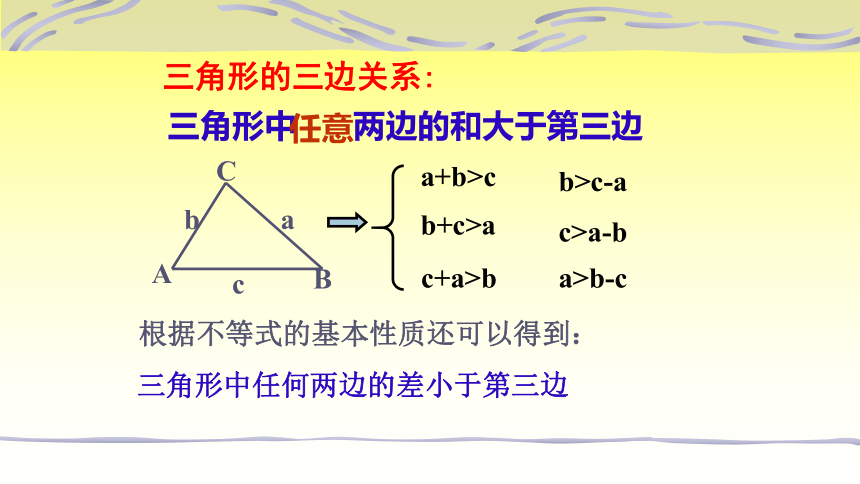
三角形的三边关系:
三角形中 两边的和大于第三边
b
c
a
A
B
C
a+b>c
b+c>a
c+a>b
任意
根据不等式的基本性质还可以得到:
三角形中任何两边的差小于第三边
b>c-a
c>a-b
a>b-c
例:长度为6cm, 4cm, 3cm三条线段能否组成三角形?
因为 6+4>3
6+3>4
4+3>6
所以能组成三角形
只要满足较小的两条线段之和大于第三条线段,便可构成三角形;若不满足,则不能构成三角形.
趁热打铁
下列长度的各组线段能否组成一个三角形?
(1)15cm、10cm、7cm (2) 4cm、5cm、10cm
(3) 3cm、8cm、5cm (4) 4cm、5cm、6cm
(2) 因为4+5<10,
所以这三条线段不能组成一个三角形.
(3) 因为3+5=8,
所以这三条线段不能组成一个三角形.
(1) 因为10+7>15,
所以这三条线段能组成一个三角形.
解:
(4) 因为4+5>6,
所以这三条线段能组成一个三角形.
考考你!
2、已知两条边长分别为2cm、5cm,
你可以画出几个符合条件的等腰三
角形?
议一议:
1、已知两条边长分别为3cm、5cm,你可以
画出几个符合条件的等腰三角形?并求符
合条件的等腰三角形的周长.
进步的标尺:
例:等腰三角形中,周长为18cm.
(1)如果腰长是底边长的2倍,求各边长;
(2)如果一边长为 4cm , 求另两边长.
解: (1) 设等腰三角形的底边为xcm,则腰长为2xcm.根据题意,得 x+2x+2x=18,
解这个方程,得 x=3.6
所以三角形的三边长为3.6cm、7.2cm、7.2cm.
(2) 若底边长为4cm,设腰长为xcm,
则有 2x+4=18,
解这个方程,得 x=7
若一条腰长为4cm,设底边长为Xcm,
则有2×4+x=18,
解这个方程,得 x=10.
因为4+4<10,
所以,以4cm为一腰不能构 成三角形.
所以,三角形的另两边长都是7cm
40cm,50cm,60cm,
90cm,130cm
40cm
90cm
已有
商店
我该买哪种呢
?
C
90cm
40cm
x
B
A
50a-ba
b
(a b)
2、已知三角形的两边a,b长分别为2和3,则第三边c的范围是
3、两根小木棍分别长3cm和5cm,现取第三根,要求长度为偶数,三根木棍作边长制成三角形,这样可制成不同的三角形有 个.
12
m-n1、若三角形的两边长分别为m和n,(设m n)则第三边y的范围是
自我PK
4、现有木棒4根,长度分别为12, 10, 8, 4, 选其中3根组成三角形,则能组成三角形的个数是( )
A.1 B.2 C.3 D.4
C
已知等腰三角形的周长为24,其中一边长为6,求其他边长.
想一想
解: 若底边长为6cm,设腰长为xcm,
则有 2x+6=24,
解这个方程,得 x=9
若一条腰长为6cm,设底边长为Xcm,
则有2×6+x=24,
解这个方程,得 x=12.
因为6+6=12,
所以,以6cm为一腰不能构 成三角形.
所以,三角形的另两边长都是9cm。
3、三角形的三边关系:
(1)判断三条已知线段能否组成三角形.
(2)已知三角形的两边,求第三边的取值范围:
知识梳理:
任何两边的和大于第三边
任何两边的差小于第三边
两边之差 第三边 两边之和
1、知道什么是三角形,会用字母表示一个三角形,包括边、角、顶点
2、会给三角形按边分类
作业:
课本 P69 第2题 、第3题
谢谢大家
再见
40cm,50cm,60cm,
90cm,130cm
我该买哪种呢?
40cm
90cm
已有
商店
你家里有新房子吗?
我喜欢带有三角形花纹的门!
三角形的三边关系
温故知新:
1、我们在小学都学过那些图形?
你能快速的画出这些图形吗?
2、通过自己的动手你认为在三角形、长方形、正方形、梯形这些图形中哪个图形最好画?
什么是三角形:
由三条不在同一直线上的线段首尾顺次连接而成的平面图形.
不在同一直线上
首尾顺次连接
A
B
C
记作△ABC
边: AB 、 AC 、 BC 、( a b c )
c
a
b
角:∠A 、 ∠B 、 ∠C(内角)
顶点:A 、 B 、 C
练一练
在下面自己画一个三角形用你喜欢的字母来表示它.
三角形按边分类
等腰三角形
(三边互不相等)
(有两条边相等)
(三条边都相等)
腰
腰
底
底角
底角
顶角
﹛
三角形
不等边三角形
﹛
腰与底不相等
腰与底相等(等边三角形)
不等边三角形
等腰三角形
等边三角形
想一想:任意给三根木棒首尾顺次连接能拼成一个三角形吗
问题1:怎样的三根木棒不能拼成三角形?
问题2:能拼成三角形的三根木棒的长度之间
有什么关系?你的依据是什么?
探索新知
2cm
3cm
6cm
3cm
4cm
6cm
三角形的三边关系:
三角形中 两边的和大于第三边
b
c
a
A
B
C
a+b>c
b+c>a
c+a>b
任意
根据不等式的基本性质还可以得到:
三角形中任何两边的差小于第三边
b>c-a
c>a-b
a>b-c
例:长度为6cm, 4cm, 3cm三条线段能否组成三角形?
因为 6+4>3
6+3>4
4+3>6
所以能组成三角形
只要满足较小的两条线段之和大于第三条线段,便可构成三角形;若不满足,则不能构成三角形.
趁热打铁
下列长度的各组线段能否组成一个三角形?
(1)15cm、10cm、7cm (2) 4cm、5cm、10cm
(3) 3cm、8cm、5cm (4) 4cm、5cm、6cm
(2) 因为4+5<10,
所以这三条线段不能组成一个三角形.
(3) 因为3+5=8,
所以这三条线段不能组成一个三角形.
(1) 因为10+7>15,
所以这三条线段能组成一个三角形.
解:
(4) 因为4+5>6,
所以这三条线段能组成一个三角形.
考考你!
2、已知两条边长分别为2cm、5cm,
你可以画出几个符合条件的等腰三
角形?
议一议:
1、已知两条边长分别为3cm、5cm,你可以
画出几个符合条件的等腰三角形?并求符
合条件的等腰三角形的周长.
进步的标尺:
例:等腰三角形中,周长为18cm.
(1)如果腰长是底边长的2倍,求各边长;
(2)如果一边长为 4cm , 求另两边长.
解: (1) 设等腰三角形的底边为xcm,则腰长为2xcm.根据题意,得 x+2x+2x=18,
解这个方程,得 x=3.6
所以三角形的三边长为3.6cm、7.2cm、7.2cm.
(2) 若底边长为4cm,设腰长为xcm,
则有 2x+4=18,
解这个方程,得 x=7
若一条腰长为4cm,设底边长为Xcm,
则有2×4+x=18,
解这个方程,得 x=10.
因为4+4<10,
所以,以4cm为一腰不能构 成三角形.
所以,三角形的另两边长都是7cm
40cm,50cm,60cm,
90cm,130cm
40cm
90cm
已有
商店
我该买哪种呢
?
C
90cm
40cm
x
B
A
50
b
(a b)
2、已知三角形的两边a,b长分别为2和3,则第三边c的范围是
3、两根小木棍分别长3cm和5cm,现取第三根,要求长度为偶数,三根木棍作边长制成三角形,这样可制成不同的三角形有 个.
1
m-n
自我PK
4、现有木棒4根,长度分别为12, 10, 8, 4, 选其中3根组成三角形,则能组成三角形的个数是( )
A.1 B.2 C.3 D.4
C
已知等腰三角形的周长为24,其中一边长为6,求其他边长.
想一想
解: 若底边长为6cm,设腰长为xcm,
则有 2x+6=24,
解这个方程,得 x=9
若一条腰长为6cm,设底边长为Xcm,
则有2×6+x=24,
解这个方程,得 x=12.
因为6+6=12,
所以,以6cm为一腰不能构 成三角形.
所以,三角形的另两边长都是9cm。
3、三角形的三边关系:
(1)判断三条已知线段能否组成三角形.
(2)已知三角形的两边,求第三边的取值范围:
知识梳理:
任何两边的和大于第三边
任何两边的差小于第三边
两边之差 第三边 两边之和
1、知道什么是三角形,会用字母表示一个三角形,包括边、角、顶点
2、会给三角形按边分类
作业:
课本 P69 第2题 、第3题
谢谢大家
再见
