沪科版七年级下数学10.3.1平行线的性质 课件(20张ppt)
文档属性
| 名称 | 沪科版七年级下数学10.3.1平行线的性质 课件(20张ppt) |
|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-05 00:00:00 | ||
图片预览



文档简介
(共20张PPT)
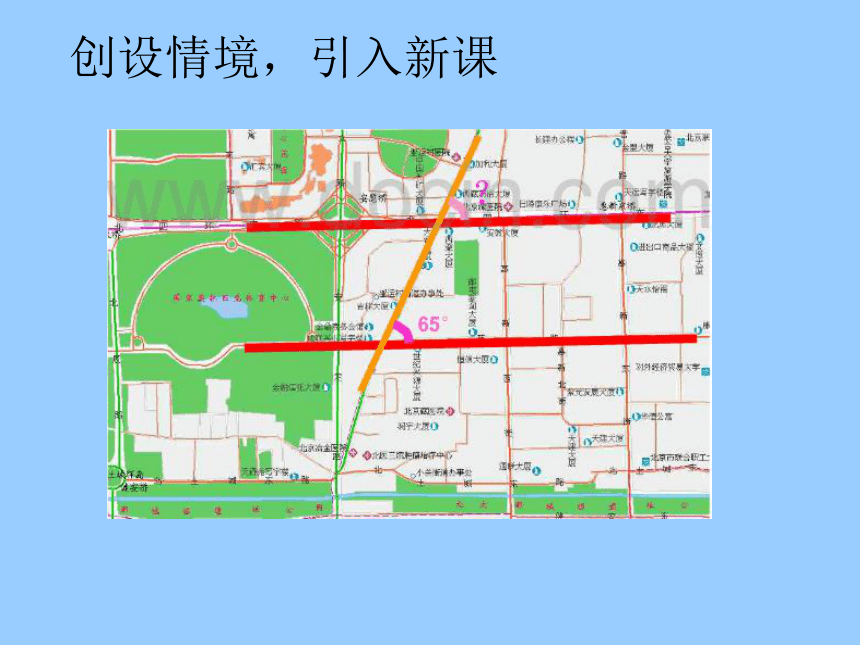
创设情境,引入新课
10.3平行线的性质(一)
回忆再现
1.如果两条直线和第三条直线平行,那么这两条直线______
2.两条直线被第三条直线所截,如果______相等(或______相等、或________互补),则这两条直线______。
同位角
内错角
同旁内角
平行
平行
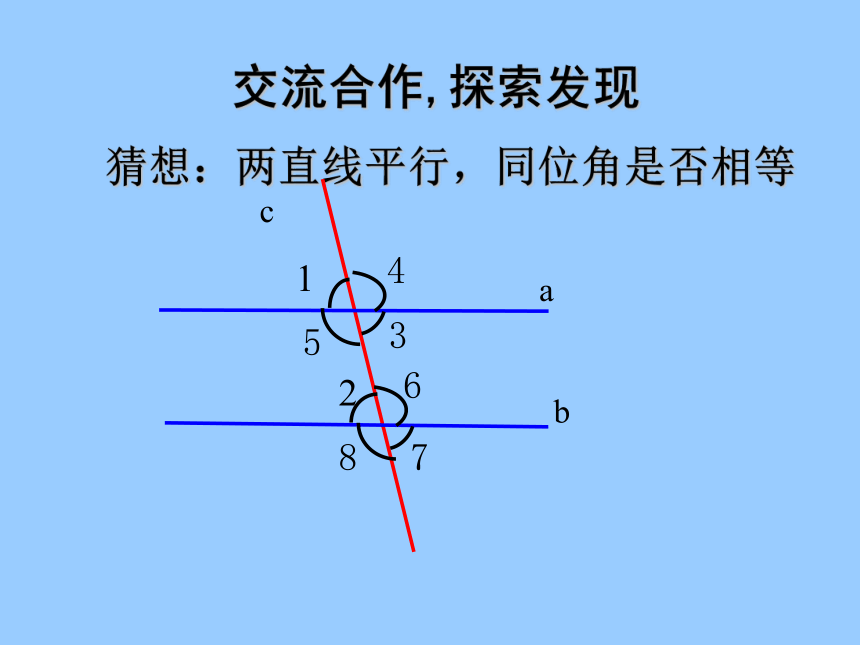
猜想:两直线平行,同位角是否相等
交流合作,探索发现
b
2
a
c
1
4
6
3
5
7
8
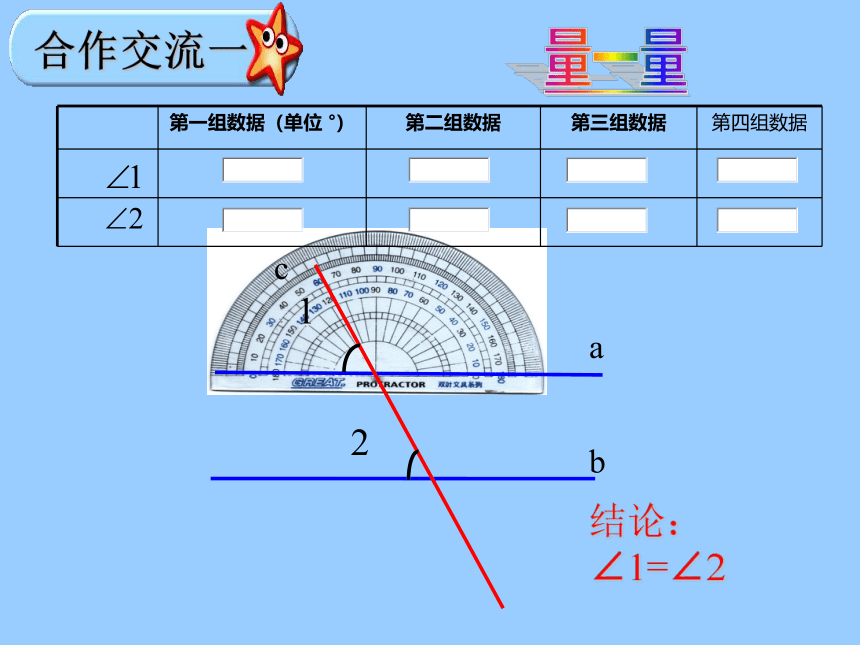
第一组数据(单位 °) 第二组数据 第三组数据 第四组数据
b
2
a
c
1
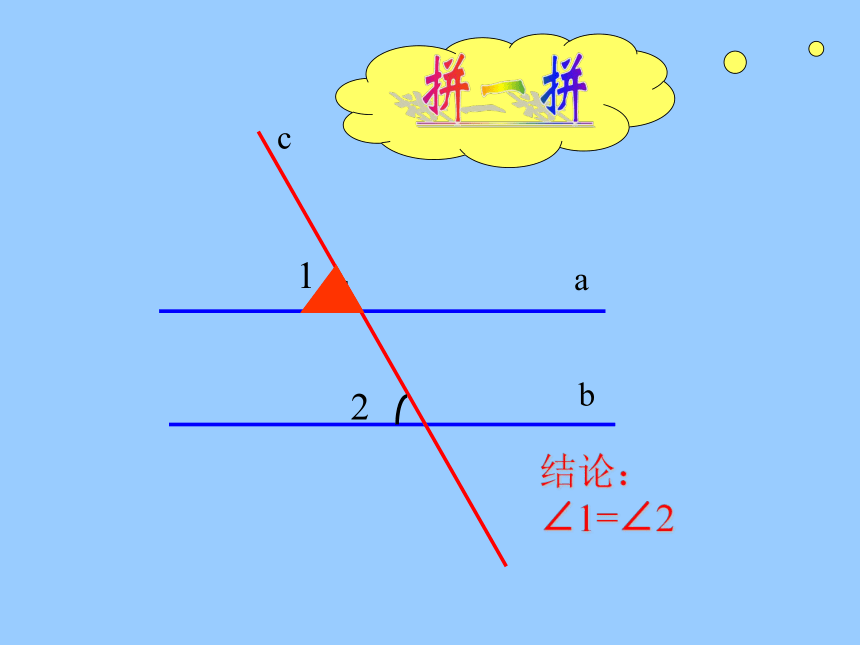
结论:∠1=∠2
合作交流一
b
2
a
c
1
结论:∠1=∠2
两直线平行,同位角相等.
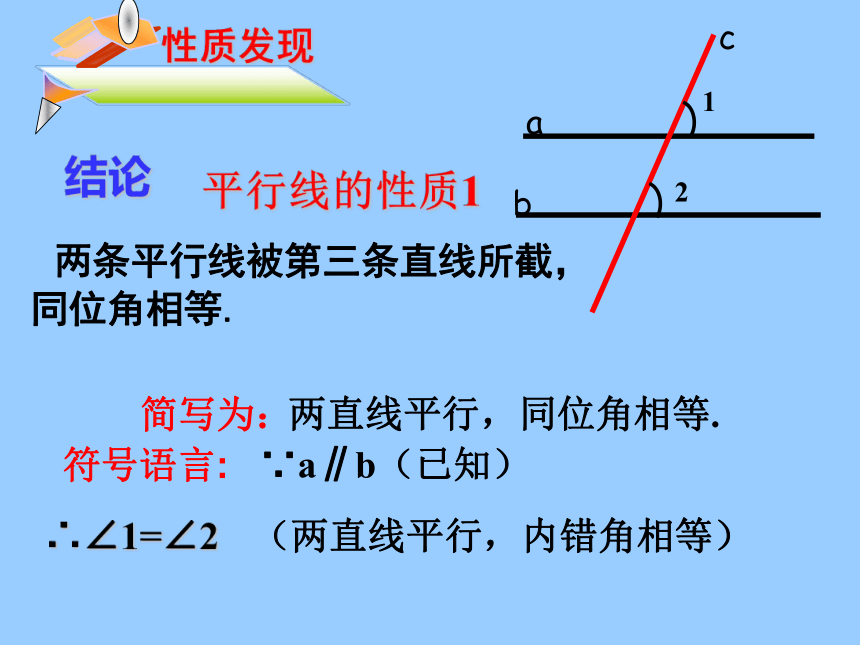
平行线的性质1
结论
两条平行线被第三条直线所截,
同位角相等.
性质发现
∴∠1=∠2
∵a∥b(已知)
简写为:
符号语言:
b
1
2
a
c
(两直线平行,内错角相等)
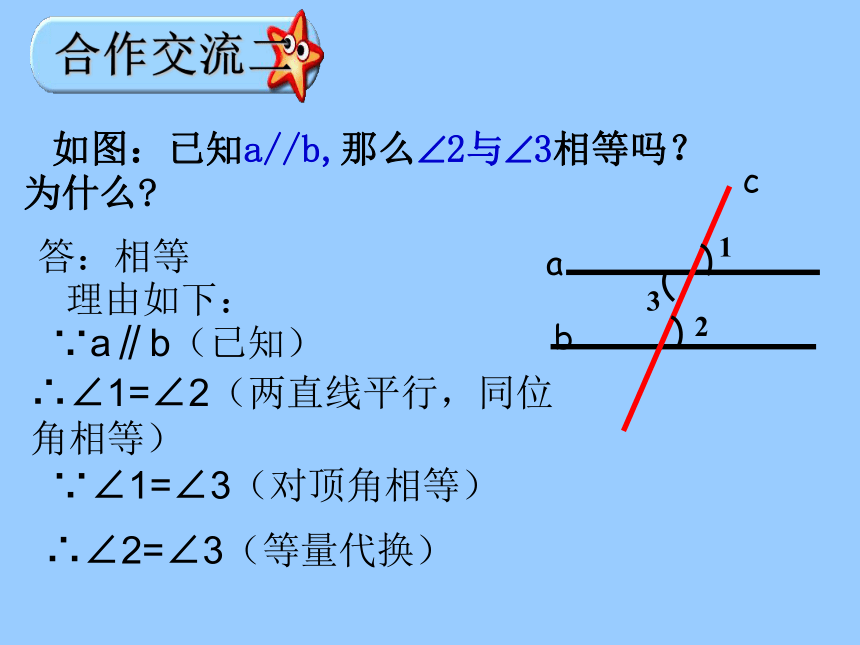
∵a∥b(已知)
∵∠1=∠3(对顶角相等)
∴∠1=∠2(两直线平行,同位角相等)
∴∠2=∠3
b
1
2
a
c
3
如图:已知a//b,那么 2与 3相等吗?
为什么
合作交流二
答:相等
理由如下:
(等量代换)
两直线平行,内错角相等.
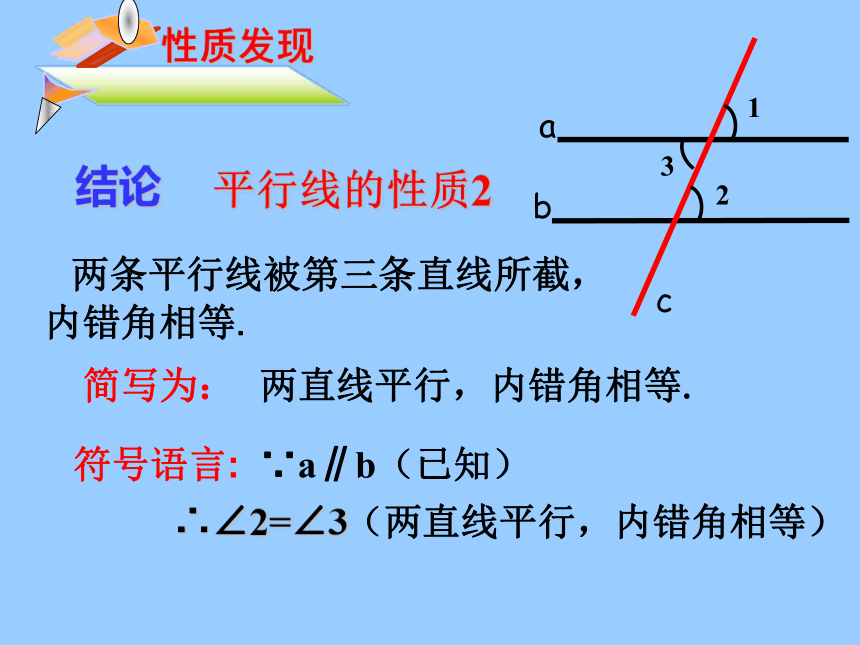
平行线的性质2
结论
两条平行线被第三条直线所截,
内错角相等.
性质发现
∴∠2=∠3
∵a∥b(已知)
符号语言:
简写为:
b
1
2
a
c
3
(两直线平行,内错角相等)
如图,已知a//b,那么 2与 4有什么关系呢?为什么
合作交流三
b
1
2
a
c
4
答:∠2+∠4=180°
∵a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等)
∵∠1+∠4=180°(邻补角定义)
∴∠2+∠4=180°(等量代换)
理由如下:
两直线平行,同旁内角互补.
平行线的性质3
结论
两条平行线被第三条直线所截,
同旁内角互补.
性质发现
∴ 2+ 4=180°(两直线平行,同位角相等)
∵a∥b(已知)
符号语言:
简写为:
b
1
2
a
c
4
两直线平行
判定
性质
已知
得到
得到
已知
说说平行线的“判定”与“性质”有什么不同
同位角相等
内错角相等
同旁内角互补
∠1
∠2
知识应用
a
b
c
已知,
直线 a∥b,∠1=65°
求∠2的度数。
解,∵a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等)
又∵∠1=65°(已知)
∴∠2=65°(等量代换)
例 如图,已知点D,E,F,分别在△ABC的边AB,AC,BC上且DE∥BC,∠B=48°.
(1)试求∠ADE的度数;
(2)如果∠DEF=48°,那么EF与AB平行吗?
解(1)∵DE∥BC(已知)
∴∠ADE=∠B(两直线平行,同位角相等)
又∵∠B=48°(已知)
∴∠ADE=48°(等量代换)
(2)由(1)得∠ADE=48°,∵∠DEF=48°(已知)
∴∠ADE=∠DEF(等量代换)
∴EF∥AB(内错角相等,两直线平行)
1、看图填空:
(1)由DE∥BC,可以得到∠1=_____,
依据是_____________________;
(2)由DE∥BC,可以得到∠6=______,
依据是______________________;
(3)由DE∥BC,可以得到∠C+____ =180°,
依据是_____________________;
(4)由DF∥AC,可以得到∠2=_______,
依据是_______________________;
(5)由DF∥AC,可以得到∠C=_______,
依据是_______________________。
∠B
两直线平行,同位角相等
∠4
两直线平行,内错角相等
∠3
两直线平行,同旁内角互补
∠4
两直线平行,内错角相等
∠6
两直线平行,同位角相等
1
4
3
2
5
6
1
2
3
4
2、如图所示,∠1=∠2,试说明∠3和∠4的关系。
a
b
解:
∵∠1=∠2
(已知)
∴a∥b
(同位角相等,两直线平行)
∴∠3=∠4
(两直线平行,内错角相等)
小 结
一、平行线的性质:
1、两直线平行,同位角相等。
2、两直线平行,内错角相等。
3、两直线平行,同旁内角互补。
二、总结了平行线的性质与判定的区别与联系
三、平行线性质的简单应用
作业布置:
课堂作业:
课本上习题10.3 第3、4两题
课外作业:基础同步练习
C
已知:如图AB∥CD, ∠ABE= 60°, ∠CDE= 32°,求∠BED的度数.
⌒
⌒
A
B
D
60°
32°
思考题:
E
创设情境,引入新课
10.3平行线的性质(一)
回忆再现
1.如果两条直线和第三条直线平行,那么这两条直线______
2.两条直线被第三条直线所截,如果______相等(或______相等、或________互补),则这两条直线______。
同位角
内错角
同旁内角
平行
平行
猜想:两直线平行,同位角是否相等
交流合作,探索发现
b
2
a
c
1
4
6
3
5
7
8
第一组数据(单位 °) 第二组数据 第三组数据 第四组数据
b
2
a
c
1
结论:∠1=∠2
合作交流一
b
2
a
c
1
结论:∠1=∠2
两直线平行,同位角相等.
平行线的性质1
结论
两条平行线被第三条直线所截,
同位角相等.
性质发现
∴∠1=∠2
∵a∥b(已知)
简写为:
符号语言:
b
1
2
a
c
(两直线平行,内错角相等)
∵a∥b(已知)
∵∠1=∠3(对顶角相等)
∴∠1=∠2(两直线平行,同位角相等)
∴∠2=∠3
b
1
2
a
c
3
如图:已知a//b,那么 2与 3相等吗?
为什么
合作交流二
答:相等
理由如下:
(等量代换)
两直线平行,内错角相等.
平行线的性质2
结论
两条平行线被第三条直线所截,
内错角相等.
性质发现
∴∠2=∠3
∵a∥b(已知)
符号语言:
简写为:
b
1
2
a
c
3
(两直线平行,内错角相等)
如图,已知a//b,那么 2与 4有什么关系呢?为什么
合作交流三
b
1
2
a
c
4
答:∠2+∠4=180°
∵a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等)
∵∠1+∠4=180°(邻补角定义)
∴∠2+∠4=180°(等量代换)
理由如下:
两直线平行,同旁内角互补.
平行线的性质3
结论
两条平行线被第三条直线所截,
同旁内角互补.
性质发现
∴ 2+ 4=180°(两直线平行,同位角相等)
∵a∥b(已知)
符号语言:
简写为:
b
1
2
a
c
4
两直线平行
判定
性质
已知
得到
得到
已知
说说平行线的“判定”与“性质”有什么不同
同位角相等
内错角相等
同旁内角互补
∠1
∠2
知识应用
a
b
c
已知,
直线 a∥b,∠1=65°
求∠2的度数。
解,∵a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等)
又∵∠1=65°(已知)
∴∠2=65°(等量代换)
例 如图,已知点D,E,F,分别在△ABC的边AB,AC,BC上且DE∥BC,∠B=48°.
(1)试求∠ADE的度数;
(2)如果∠DEF=48°,那么EF与AB平行吗?
解(1)∵DE∥BC(已知)
∴∠ADE=∠B(两直线平行,同位角相等)
又∵∠B=48°(已知)
∴∠ADE=48°(等量代换)
(2)由(1)得∠ADE=48°,∵∠DEF=48°(已知)
∴∠ADE=∠DEF(等量代换)
∴EF∥AB(内错角相等,两直线平行)
1、看图填空:
(1)由DE∥BC,可以得到∠1=_____,
依据是_____________________;
(2)由DE∥BC,可以得到∠6=______,
依据是______________________;
(3)由DE∥BC,可以得到∠C+____ =180°,
依据是_____________________;
(4)由DF∥AC,可以得到∠2=_______,
依据是_______________________;
(5)由DF∥AC,可以得到∠C=_______,
依据是_______________________。
∠B
两直线平行,同位角相等
∠4
两直线平行,内错角相等
∠3
两直线平行,同旁内角互补
∠4
两直线平行,内错角相等
∠6
两直线平行,同位角相等
1
4
3
2
5
6
1
2
3
4
2、如图所示,∠1=∠2,试说明∠3和∠4的关系。
a
b
解:
∵∠1=∠2
(已知)
∴a∥b
(同位角相等,两直线平行)
∴∠3=∠4
(两直线平行,内错角相等)
小 结
一、平行线的性质:
1、两直线平行,同位角相等。
2、两直线平行,内错角相等。
3、两直线平行,同旁内角互补。
二、总结了平行线的性质与判定的区别与联系
三、平行线性质的简单应用
作业布置:
课堂作业:
课本上习题10.3 第3、4两题
课外作业:基础同步练习
C
已知:如图AB∥CD, ∠ABE= 60°, ∠CDE= 32°,求∠BED的度数.
⌒
⌒
A
B
D
60°
32°
思考题:
E
