沪科版数学九年级上册 22.3 相似三角形的性质 教案
文档属性
| 名称 | 沪科版数学九年级上册 22.3 相似三角形的性质 教案 |
|
|
| 格式 | docx | ||
| 文件大小 | 79.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-04 14:47:45 | ||
图片预览

文档简介
22.3.1相似三角形的性质
1.知识与技能:探索相似三角形性质定理1,使学生掌握定理1并加以应用。
2.过程与方法:通过对性质定理1的探究,使学生经历观察、猜想、论证、归纳的过程,培养学生主动探究的能力、推理的能力。
3.情感态度与价值观:通过相似三角形性质及应用的探究学习,培养学生类比思想、归纳思想及特殊到一般的认识规律,拓展学生的几何思维。
二、教学重难点
1.教学重点:相似三角形对应高、对应中线、对应角平分线之比都等于相似比。
2.教学难点:相似三角形性质定理1的应用。
三、教学过程
教学环 节 教学内容
复习引 入 相似三角形的定义: 相似三角形的判定方法: 已经学习的相似三角形的性质: 那么它还有哪些性质呢?对于一个三角形而言,除了角和边,还有哪些重要的元素呢?
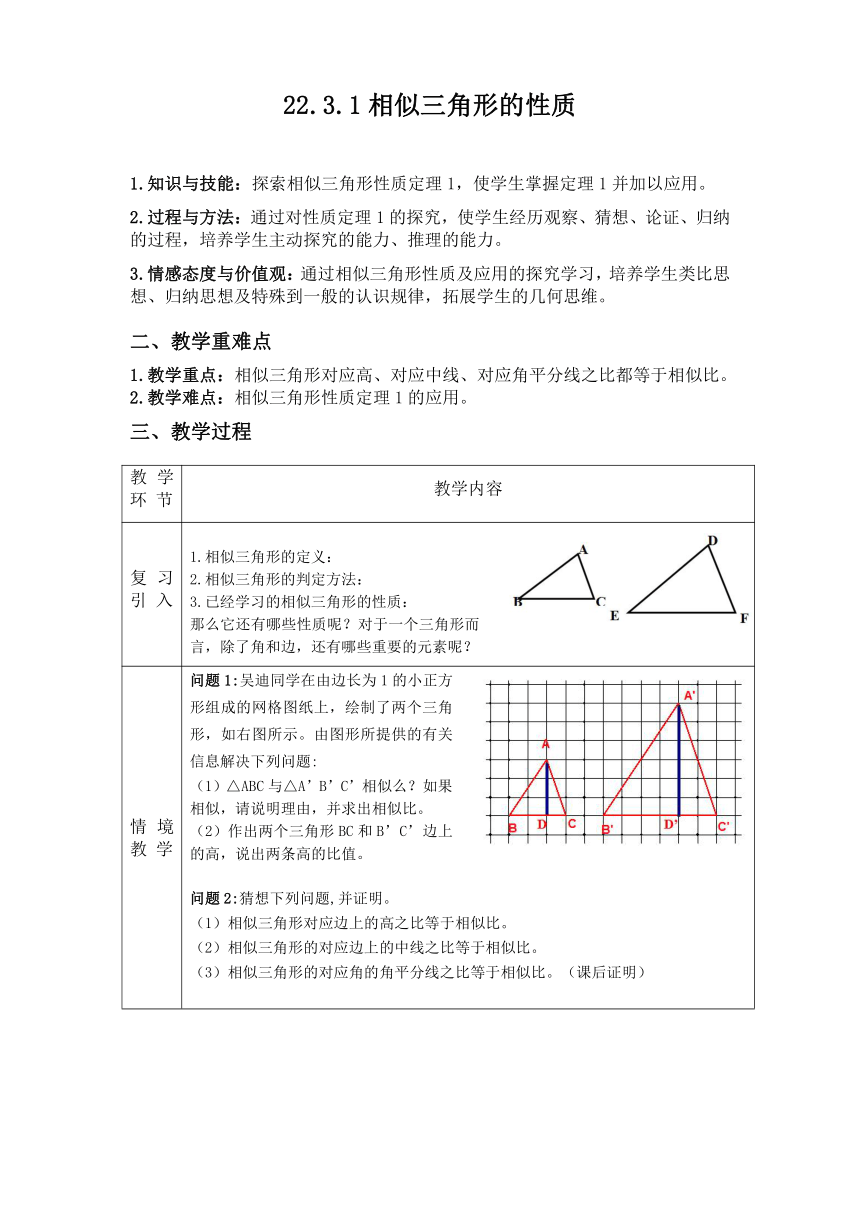
情境教 学 问题1:吴迪同学在由边长为1的小正方形组成的网格图纸上,绘制了两个三角形,如右图所示。由图形所提供的有关信息解决下列问题: (1)△ABC与△A’B’C’相似么?如果相似,请说明理由,并求出相似比。 (2)作出两个三角形BC和B’C’边上的高,说出两条高的比值。 问题2:猜想下列问题,并证明。 相似三角形对应边上的高之比等于相似比。 相似三角形的对应边上的中线之比等于相似比。 相似三角形的对应角的角平分线之比等于相似比。(课后证明)
情境教 学 结论:相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比。 问题3:课堂练习 已知△ABC∽△DEF,BG、EH分△ABC和 △DEF的角平分线,BC=6cm,EF=4cm,BG=4.8cm.求EH的长.
典型例 题 例题:如图, △ABC是一块锐角三角形的余料,边长 BC=60cm,高AD=40cm,要把它加工成正方形零件,使正方形的一边FG在BC上,其余两个顶点E、H分别在AB、AC上,高AD与EH相交于点P. (1)△AEH与△ABC相似么?为什么? (2)求这个正方形的零件的边长。
变 式训 练 变式1:已知:如图,FGHI为矩形,AD⊥BC于D, , BC=30cm,AD=12cm . 求:矩形FGNI的周长(面积) 变式2:如图,矩形FGHN内接于△ABC,FG在BC上,NH分别在AB、AC上,且AD⊥BC于D,交NH于E,AD=8cm,BC=24cm,(1)设NF=x,用含有x的式子表示NH; (2)求矩形FGHN的面积的最大值。
课堂小 结 相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比; 定理的应用:设未知数;与二次函数的结合。
作业布 置 同步练习22.3(一)
(
相似三角形性质(1)
性质 定理 例题
定理 证明 板演
)四、板书设计
五、教学反思
1.知识与技能:探索相似三角形性质定理1,使学生掌握定理1并加以应用。
2.过程与方法:通过对性质定理1的探究,使学生经历观察、猜想、论证、归纳的过程,培养学生主动探究的能力、推理的能力。
3.情感态度与价值观:通过相似三角形性质及应用的探究学习,培养学生类比思想、归纳思想及特殊到一般的认识规律,拓展学生的几何思维。
二、教学重难点
1.教学重点:相似三角形对应高、对应中线、对应角平分线之比都等于相似比。
2.教学难点:相似三角形性质定理1的应用。
三、教学过程
教学环 节 教学内容
复习引 入 相似三角形的定义: 相似三角形的判定方法: 已经学习的相似三角形的性质: 那么它还有哪些性质呢?对于一个三角形而言,除了角和边,还有哪些重要的元素呢?
情境教 学 问题1:吴迪同学在由边长为1的小正方形组成的网格图纸上,绘制了两个三角形,如右图所示。由图形所提供的有关信息解决下列问题: (1)△ABC与△A’B’C’相似么?如果相似,请说明理由,并求出相似比。 (2)作出两个三角形BC和B’C’边上的高,说出两条高的比值。 问题2:猜想下列问题,并证明。 相似三角形对应边上的高之比等于相似比。 相似三角形的对应边上的中线之比等于相似比。 相似三角形的对应角的角平分线之比等于相似比。(课后证明)
情境教 学 结论:相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比。 问题3:课堂练习 已知△ABC∽△DEF,BG、EH分△ABC和 △DEF的角平分线,BC=6cm,EF=4cm,BG=4.8cm.求EH的长.
典型例 题 例题:如图, △ABC是一块锐角三角形的余料,边长 BC=60cm,高AD=40cm,要把它加工成正方形零件,使正方形的一边FG在BC上,其余两个顶点E、H分别在AB、AC上,高AD与EH相交于点P. (1)△AEH与△ABC相似么?为什么? (2)求这个正方形的零件的边长。
变 式训 练 变式1:已知:如图,FGHI为矩形,AD⊥BC于D, , BC=30cm,AD=12cm . 求:矩形FGNI的周长(面积) 变式2:如图,矩形FGHN内接于△ABC,FG在BC上,NH分别在AB、AC上,且AD⊥BC于D,交NH于E,AD=8cm,BC=24cm,(1)设NF=x,用含有x的式子表示NH; (2)求矩形FGHN的面积的最大值。
课堂小 结 相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比; 定理的应用:设未知数;与二次函数的结合。
作业布 置 同步练习22.3(一)
(
相似三角形性质(1)
性质 定理 例题
定理 证明 板演
)四、板书设计
五、教学反思
