2021-2022学年高一下学期数学北师大版(2019)必修第二册1.6 函数y=Asin(ωx+φ)的性质与图象(第一课时)课件(共28张PPT)
文档属性
| 名称 | 2021-2022学年高一下学期数学北师大版(2019)必修第二册1.6 函数y=Asin(ωx+φ)的性质与图象(第一课时)课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-04 00:00:00 | ||
图片预览








文档简介
(共28张PPT)
1.6 §函数y=Asin(ωx+φ)的性质与图象
第一课时 探究ω对y=sin ωx的图象的影响
北师大(2019)必修2
琪
胡
聚焦知识目标
1.探讨ω对y=sinωx的图象的影响.
2.探讨ω对y=sinωx的性质的影响.
数学素养
1.通过图象变换,培养直观想象素养.
2.通过对y=sinωx性质研究 ,培养数学运算和建模素养.
环节一
引入新课
引入新课
“南昌之星”摩天轮于2006年竣工,总高度160m,直径153m,匀速旋转一圈需时30min,以摩天轮的中心为原点建立平面直角坐标系,画示意图,如图
A
设座舱A为起始位置如图,OA与x轴所形成的角的大小为,因为转一圈需要30min,所以每分所转的角度为
经过xmin后,OA旋转到OA'.OA’与x轴所形成角的大小为x-
因为直径为153m,总高度为160m,所以OA的长为76.5m,轮子的最低点与地面距离为160-153=7(m),原点O距离地面的距离为7+76.5=83.5(m),从而点到地面的距离y与时间x的关系为:y= 76.
O
引入新课
y= 76.
A
ω
B
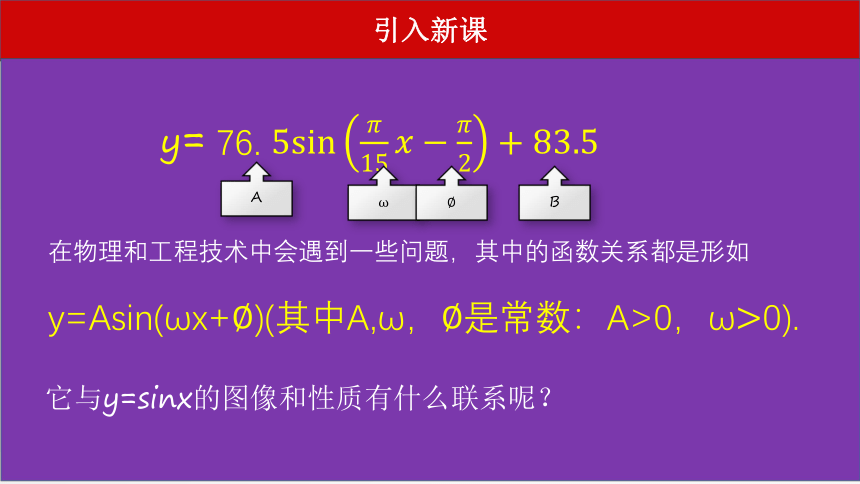
在物理和工程技术中会遇到一些问题,其中的函数关系都是形如
y=Asin(ωx+ )(其中A,ω, 是常数:A>0,ω>0).
它与y=sinx的图像和性质有什么联系呢?
环节二
对y=sin2x图象和性质的研究
y=sin2x(x∈R)周期
实例分析
由sin2x=sin(2x+2π)=sin 2(x+π),根据周期函数的定义,y=sin2x是周期函数,π是y=sin2x的最小正周期,
y=sin2x(x∈R)图象
五点法
在函数y=sinx五个关键点的基础上,列表
2x 0 π
x 0 π
y=sin2x 0 1 0 -1 0
由此得到函数y=sin2x的五个关键点为
画出该函数在一个周期[0,π]上的图象
x
0
y
由函数y=sin2x的周期性,把图象向左、右延拓
y=sin2x(x∈R)图象
伸缩变换
从函数y=sin2x的图象看出,将函数y=sinx图象上每个点的横坐标都缩短为原来.的,纵坐标不变.就得到函数y=sin2x的图象,且最小正周期变为π.
x
0
y
2
y=sinx
y=sin2x
y=sin2x(x∈R)单调性
实例分析
从图象上可以看出,函数y=sin2x在区间[ 上单调递增:在区间 上单调递减.
x
0
y
y=sin2x(x∈R)最值或值域
实例分析
在区间[0,π]上,当 时,函数y=sin2x取得最大值1;当 时,函数y=sin2x取得最小值-1.由函数y=sin2x的周期性可知,当 时,它取得最大值1;当 时,它取得最小值-1.
x
0
y
环节三
对y=sinx图象和性质的研究
y=sinx(x∈R)图象与性质
实例分析
例1求函数 的周期,并画出其图象.
解:由y=sinx的周期性可知 根据周期函数的定义, 是周期函数,6π是它的最小正周期
在函数y=sinx五个关键点的基础上,列表
y=sinx(x∈R)图象与性质
五点法
例1求函数 的周期,并画出其图象.
0 π
x 0 3π
0 1 0 -1 0
由此得到函数 的五个关键点为画出该函数在一个周期[0,6π]上的图象.由函数 的周期性,把图象向左、延拓,得到 在R上的图象
y=sinx(x∈R)图象与性质
伸缩变换
例1求函数 的周期,并画出其图象.
从函数 的图象看出,对同一个x值.将函数y=sin x图象上每个点的横坐标都伸长到原来的3倍,纵坐标不变,就得到函数 的图象
y=sinx
y=sin x
环节四
ω对y=sinωx图像和性质的影响
ω对y=sinωx图像和性质的影响
周期
一般地,对于ω>0,有
sinωx=sin(ωx+2π)=sinω(x+)
根据周期函数的定义,T= 是函数y= sinωx的最小正周期.
通常称周期的倒数=为频率.
ω对y=sinωx图像和性质的影响
图象变换
函数y=sinωx的图象是将函数y=sinx图象上所有点的横坐标缩短到原来的.(当ω>1时)或伸长(当0<ω<1时)到原来的(纵坐标不变)得到的.
环节五
知识应用
知识应用
周期
1.求下列函数的周期;
提示
图象法
定义法
公式法
知识应用
周期
1.求下列函数的周期;
解(1)T==8π
(2)T==
知识应用
2.将函数y=sin x的图象上所有点的横坐标缩短到原
来的 (纵坐标不变)得____的图象.
图象变换
【解析】依题意知将y=sin x图象上所有点的横坐标缩短到原来的 后可得y=sin6x的图象.
知识应用
3. 函数y=sin x的图象与y=sinx的图象有什么关系?
图象变换
将y=sin x图象上所有点的横坐标伸长到原来的 倍 后可得y=sin x的图象.
知识应用
图象与性质
提示
五点法
变换法
4.画出函数y=sin4x在一个周期上的图象,并讨论其性质:
知识应用
图象与性质
4.画出函数y=sin4x在一个周期上的图象,并讨论其性质:
y=sinx
y=sin4x
对于y=sin4x
周期,奇函数,值域[-1,1],增区间[-, +],减区间[+, +](k∈z)
练习
若将函数y=sinx的图象上所有点的纵坐标变,横坐标变为原来的,则所得图象对应的函数解析式为
将函数y=snx的图象上所有点的纵坐标不变,横坐标变为原来的,所以x的系数变为原来的2倍,即函数解析式变为y=sin2x.
胡琪老师制作
1.6 §函数y=Asin(ωx+φ)的性质与图象
第一课时 探究ω对y=sin ωx的图象的影响
北师大(2019)必修2
琪
胡
聚焦知识目标
1.探讨ω对y=sinωx的图象的影响.
2.探讨ω对y=sinωx的性质的影响.
数学素养
1.通过图象变换,培养直观想象素养.
2.通过对y=sinωx性质研究 ,培养数学运算和建模素养.
环节一
引入新课
引入新课
“南昌之星”摩天轮于2006年竣工,总高度160m,直径153m,匀速旋转一圈需时30min,以摩天轮的中心为原点建立平面直角坐标系,画示意图,如图
A
设座舱A为起始位置如图,OA与x轴所形成的角的大小为,因为转一圈需要30min,所以每分所转的角度为
经过xmin后,OA旋转到OA'.OA’与x轴所形成角的大小为x-
因为直径为153m,总高度为160m,所以OA的长为76.5m,轮子的最低点与地面距离为160-153=7(m),原点O距离地面的距离为7+76.5=83.5(m),从而点到地面的距离y与时间x的关系为:y= 76.
O
引入新课
y= 76.
A
ω
B
在物理和工程技术中会遇到一些问题,其中的函数关系都是形如
y=Asin(ωx+ )(其中A,ω, 是常数:A>0,ω>0).
它与y=sinx的图像和性质有什么联系呢?
环节二
对y=sin2x图象和性质的研究
y=sin2x(x∈R)周期
实例分析
由sin2x=sin(2x+2π)=sin 2(x+π),根据周期函数的定义,y=sin2x是周期函数,π是y=sin2x的最小正周期,
y=sin2x(x∈R)图象
五点法
在函数y=sinx五个关键点的基础上,列表
2x 0 π
x 0 π
y=sin2x 0 1 0 -1 0
由此得到函数y=sin2x的五个关键点为
画出该函数在一个周期[0,π]上的图象
x
0
y
由函数y=sin2x的周期性,把图象向左、右延拓
y=sin2x(x∈R)图象
伸缩变换
从函数y=sin2x的图象看出,将函数y=sinx图象上每个点的横坐标都缩短为原来.的,纵坐标不变.就得到函数y=sin2x的图象,且最小正周期变为π.
x
0
y
2
y=sinx
y=sin2x
y=sin2x(x∈R)单调性
实例分析
从图象上可以看出,函数y=sin2x在区间[ 上单调递增:在区间 上单调递减.
x
0
y
y=sin2x(x∈R)最值或值域
实例分析
在区间[0,π]上,当 时,函数y=sin2x取得最大值1;当 时,函数y=sin2x取得最小值-1.由函数y=sin2x的周期性可知,当 时,它取得最大值1;当 时,它取得最小值-1.
x
0
y
环节三
对y=sinx图象和性质的研究
y=sinx(x∈R)图象与性质
实例分析
例1求函数 的周期,并画出其图象.
解:由y=sinx的周期性可知 根据周期函数的定义, 是周期函数,6π是它的最小正周期
在函数y=sinx五个关键点的基础上,列表
y=sinx(x∈R)图象与性质
五点法
例1求函数 的周期,并画出其图象.
0 π
x 0 3π
0 1 0 -1 0
由此得到函数 的五个关键点为画出该函数在一个周期[0,6π]上的图象.由函数 的周期性,把图象向左、延拓,得到 在R上的图象
y=sinx(x∈R)图象与性质
伸缩变换
例1求函数 的周期,并画出其图象.
从函数 的图象看出,对同一个x值.将函数y=sin x图象上每个点的横坐标都伸长到原来的3倍,纵坐标不变,就得到函数 的图象
y=sinx
y=sin x
环节四
ω对y=sinωx图像和性质的影响
ω对y=sinωx图像和性质的影响
周期
一般地,对于ω>0,有
sinωx=sin(ωx+2π)=sinω(x+)
根据周期函数的定义,T= 是函数y= sinωx的最小正周期.
通常称周期的倒数=为频率.
ω对y=sinωx图像和性质的影响
图象变换
函数y=sinωx的图象是将函数y=sinx图象上所有点的横坐标缩短到原来的.(当ω>1时)或伸长(当0<ω<1时)到原来的(纵坐标不变)得到的.
环节五
知识应用
知识应用
周期
1.求下列函数的周期;
提示
图象法
定义法
公式法
知识应用
周期
1.求下列函数的周期;
解(1)T==8π
(2)T==
知识应用
2.将函数y=sin x的图象上所有点的横坐标缩短到原
来的 (纵坐标不变)得____的图象.
图象变换
【解析】依题意知将y=sin x图象上所有点的横坐标缩短到原来的 后可得y=sin6x的图象.
知识应用
3. 函数y=sin x的图象与y=sinx的图象有什么关系?
图象变换
将y=sin x图象上所有点的横坐标伸长到原来的 倍 后可得y=sin x的图象.
知识应用
图象与性质
提示
五点法
变换法
4.画出函数y=sin4x在一个周期上的图象,并讨论其性质:
知识应用
图象与性质
4.画出函数y=sin4x在一个周期上的图象,并讨论其性质:
y=sinx
y=sin4x
对于y=sin4x
周期,奇函数,值域[-1,1],增区间[-, +],减区间[+, +](k∈z)
练习
若将函数y=sinx的图象上所有点的纵坐标变,横坐标变为原来的,则所得图象对应的函数解析式为
将函数y=snx的图象上所有点的纵坐标不变,横坐标变为原来的,所以x的系数变为原来的2倍,即函数解析式变为y=sin2x.
胡琪老师制作
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
