沪科版七年级下数学 10.2平行线的判定课件(23张ppt)
文档属性
| 名称 | 沪科版七年级下数学 10.2平行线的判定课件(23张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 513.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-05 00:00:00 | ||
图片预览



文档简介
(共23张PPT)
10.2平行线的判定
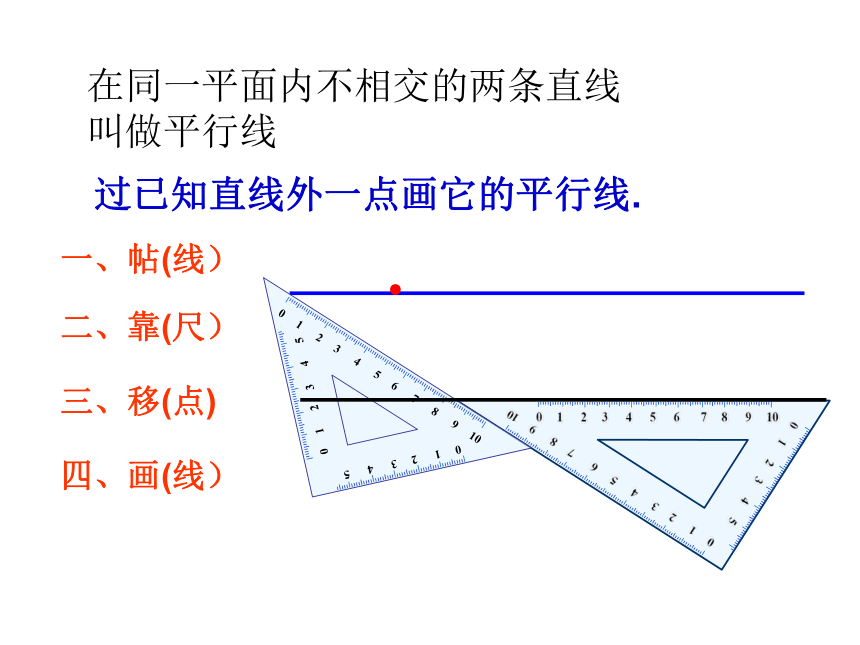
一、帖(线)
二、靠(尺)
三、移(点)
四、画(线)
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
●
过已知直线外一点画它的平行线.
在同一平面内不相交的两条直线叫做平行线
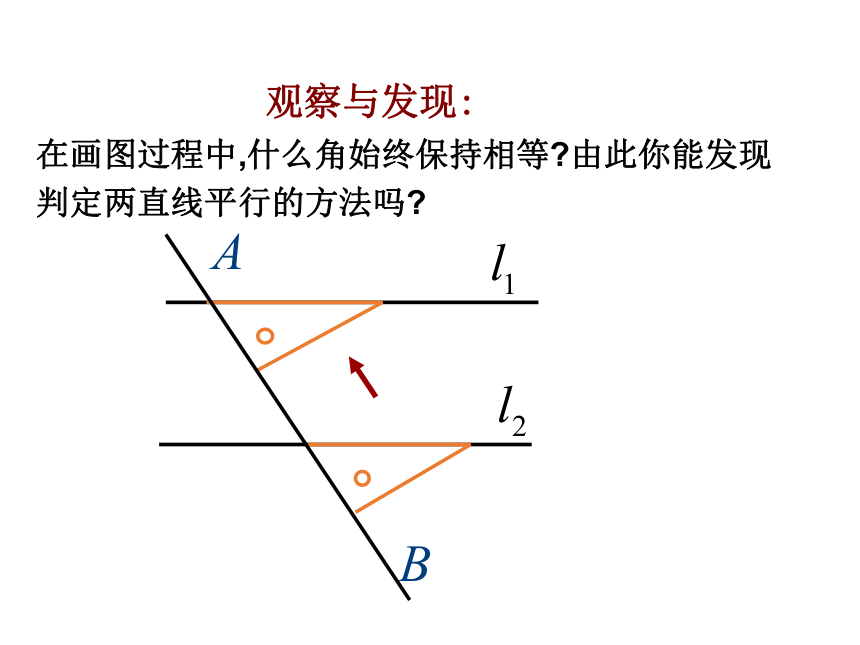
观察与发现:
在画图过程中,什么角始终保持相等 由此你能发现判定两直线平行的方法吗
一般地,判断两直线平行有下面的方法:
判定方法1 两条直线被第三条直线所截 ,
如果同位角相等, 那么这两条直线平行.
简单说成:同位角相等,两直线平行.
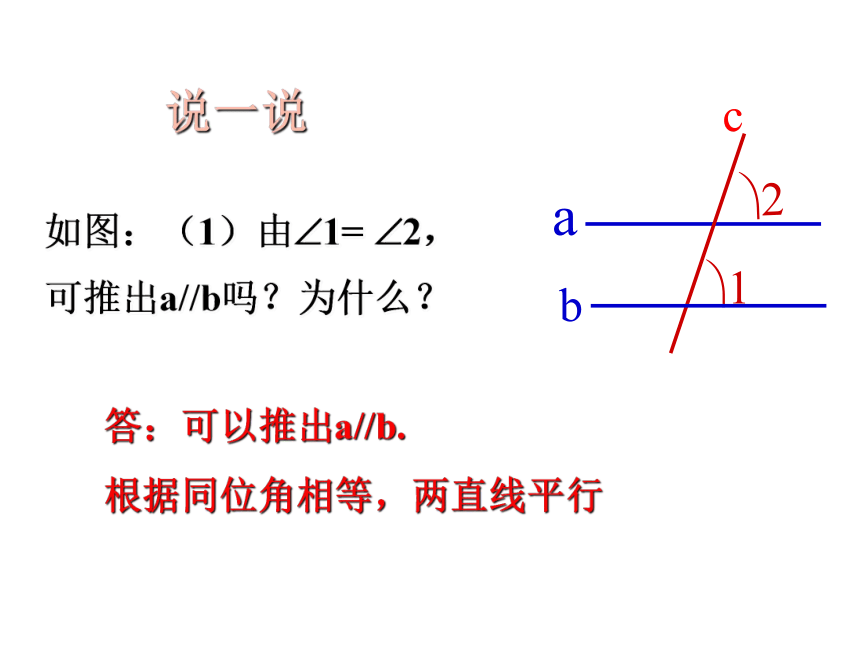
如图:(1)由 1= 2,
可推出a//b吗?为什么?
说一说
答:可以推出a//b.
根据同位角相等,两直线平行
1
2
a
b
c
1
2
a
b
c
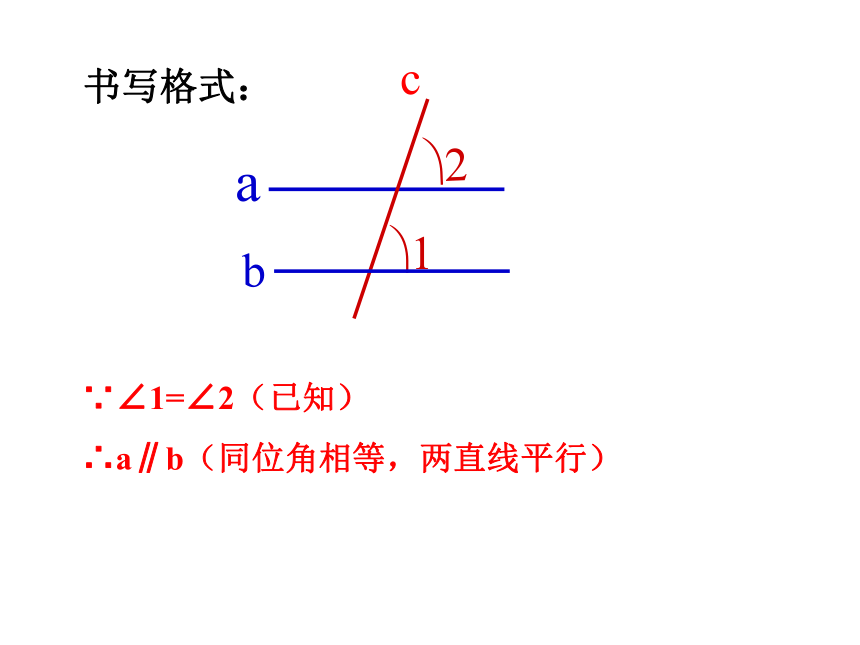
∵∠1=∠2(已知)
∴a∥b(同位角相等,两直线平行)
书写格式:
4
1
2
3
A
B
C
E
F
D
5
H
G
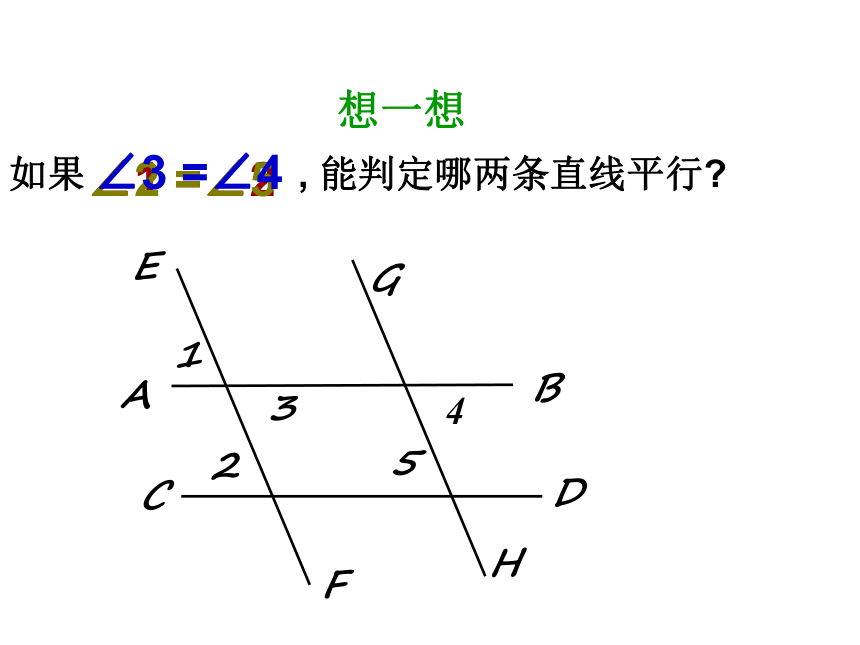
如果 , 能判定哪两条直线平行
∠1 =∠2
∠2 =∠5
∠3 =∠4
想一想
两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角,由同位角相等可以判定两直线平行,那么,能否利用内错角,或同旁内角来判定两直线平行呢?
思考:
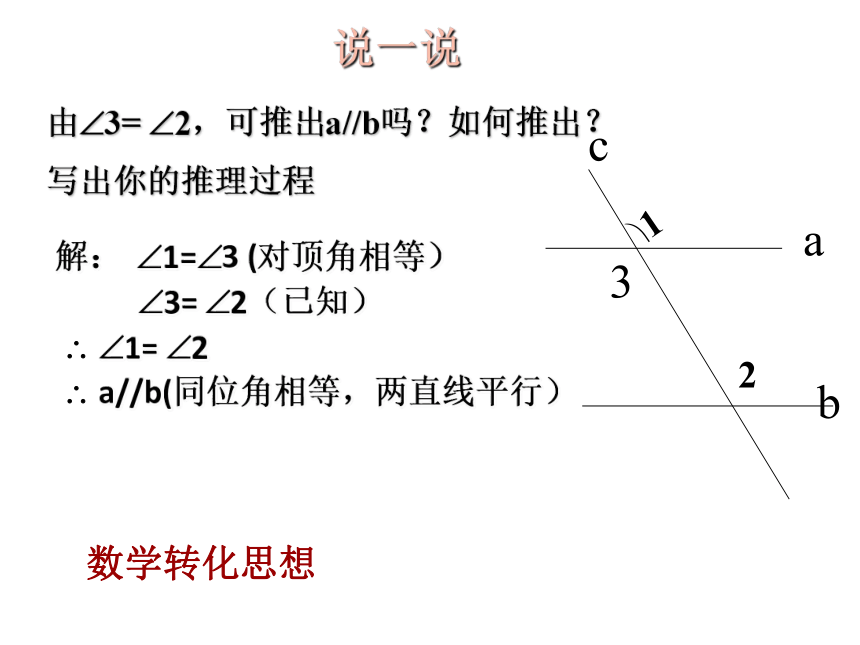
由 3= 2,可推出a//b吗?如何推出?
写出你的推理过程
解: 1= 3 (对顶角相等)
3= 2(已知)
1= 2
a//b(同位角相等,两直线平行)
2
1
c
b
a
3
说一说
数学转化思想
判定方法2 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行
简单说成:内错角相等,两直线平行
一般地,判断两直线平行有下面的方法:
如图,∠1= ∠2 ,且∠1=∠3, AB和CD平行吗?
A
B
C
D
1
2
3
想一想
如果 1+ 2=1800 能判定a//b吗
c
解:能,
因为 1+ 2=180
1+ 3=180
所以 2= 3
所以 a//b
2
b
a
1
3
说一说
数学转化思想
判定方法3 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行
简单说成:同旁内角互补,两直线平行
一般地,判断两直线平行有下面的方法:
如图: B= D=45°, C=135°,问图中有
哪些直线平行?
答:AB//CD,AD//BC
∵ B=45°(已知)
C=135°(已知)
B+ C=180°
AB//CD(同旁内角互补,两直线平行)
同理:AD//BC
D
C
B
A
想一想
同位角相等,两直线平行;
内错角相等,两直线平行;
同旁内角互补,两直线平行;
归纳
判定两条直线平行的方法
文字叙述 符号语言 图形
相等
两直线平行 ∵ (已知)
∴a∥b
相等
两直线平行 ∵ (已知)
∴a∥b
互补,两直线平行 ∵
∴a∥b
同位角
内错角
同旁内角
∠3=∠4
∠1=∠4
∠2+∠4=180°
1
4
3
2
A
D
C
B
1、如图,不能判定 的是 ( )
能力挑战
(A)∠2=∠3 (B)∠1=∠4
(C)∠1=∠2 (D)∠1=∠3
D
能力挑战
2、如图,∠1=∠2,则下列结论正确的是( )
(A)AD//BC (B)AB//CD
(C)AD//EF (D)EF//BC
C
3.如图,哪些条件能判定直线AB∥CD
1
4
3
2
A
D
C
B
能力挑战
4.如图:可以确定AB∥CE的条件是( )
A.∠2=∠B
B. ∠1=∠A
C. ∠3=∠B
D. ∠3=∠A
A E
B C D
1
2
3
C
能力挑战
(1)从∠1=∠2,可以推出 ∥ ,
理由是 .
(2)从∠2=∠ ,可以推出c∥d ,
理由是 .
(3)如果∠1=75°,∠4=105°,
可以推出 ∥ .
理由是 .
练一练
b
a
内错角相等,两直线平行
同位角相等,两直线平行
3
a
b
4
c
2
d
3
1
a
b
同旁内角互补,两直线平行
1.如图
从∠1=∠4,可以推出 ∥ ,
理由是 .
(2)从∠ABC +∠ =180,可以推出AB∥CD ,
理由是 .
(3)从∠ =∠ ,可以推出AD∥BC,
理由是 .
A
B
C
D
1
2
3
4
5
(4)从∠5=∠ ,可以推出AB∥CD,
理由是 .
AB
内错角相等,两直线平行
CD
BCD
同旁内角互补,两直线平行
2
3
内错角相等,两直线平行
ABC
同位角相等,两直线平行
2.如图
平行线判定方法1:同位角相等,两直线平行。
平行线判定方法2:内错角相等,两直线平行。
平行线判定方法2:同旁内角互补,两直线平行。
10.2平行线的判定
一、帖(线)
二、靠(尺)
三、移(点)
四、画(线)
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
●
过已知直线外一点画它的平行线.
在同一平面内不相交的两条直线叫做平行线
观察与发现:
在画图过程中,什么角始终保持相等 由此你能发现判定两直线平行的方法吗
一般地,判断两直线平行有下面的方法:
判定方法1 两条直线被第三条直线所截 ,
如果同位角相等, 那么这两条直线平行.
简单说成:同位角相等,两直线平行.
如图:(1)由 1= 2,
可推出a//b吗?为什么?
说一说
答:可以推出a//b.
根据同位角相等,两直线平行
1
2
a
b
c
1
2
a
b
c
∵∠1=∠2(已知)
∴a∥b(同位角相等,两直线平行)
书写格式:
4
1
2
3
A
B
C
E
F
D
5
H
G
如果 , 能判定哪两条直线平行
∠1 =∠2
∠2 =∠5
∠3 =∠4
想一想
两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角,由同位角相等可以判定两直线平行,那么,能否利用内错角,或同旁内角来判定两直线平行呢?
思考:
由 3= 2,可推出a//b吗?如何推出?
写出你的推理过程
解: 1= 3 (对顶角相等)
3= 2(已知)
1= 2
a//b(同位角相等,两直线平行)
2
1
c
b
a
3
说一说
数学转化思想
判定方法2 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行
简单说成:内错角相等,两直线平行
一般地,判断两直线平行有下面的方法:
如图,∠1= ∠2 ,且∠1=∠3, AB和CD平行吗?
A
B
C
D
1
2
3
想一想
如果 1+ 2=1800 能判定a//b吗
c
解:能,
因为 1+ 2=180
1+ 3=180
所以 2= 3
所以 a//b
2
b
a
1
3
说一说
数学转化思想
判定方法3 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行
简单说成:同旁内角互补,两直线平行
一般地,判断两直线平行有下面的方法:
如图: B= D=45°, C=135°,问图中有
哪些直线平行?
答:AB//CD,AD//BC
∵ B=45°(已知)
C=135°(已知)
B+ C=180°
AB//CD(同旁内角互补,两直线平行)
同理:AD//BC
D
C
B
A
想一想
同位角相等,两直线平行;
内错角相等,两直线平行;
同旁内角互补,两直线平行;
归纳
判定两条直线平行的方法
文字叙述 符号语言 图形
相等
两直线平行 ∵ (已知)
∴a∥b
相等
两直线平行 ∵ (已知)
∴a∥b
互补,两直线平行 ∵
∴a∥b
同位角
内错角
同旁内角
∠3=∠4
∠1=∠4
∠2+∠4=180°
1
4
3
2
A
D
C
B
1、如图,不能判定 的是 ( )
能力挑战
(A)∠2=∠3 (B)∠1=∠4
(C)∠1=∠2 (D)∠1=∠3
D
能力挑战
2、如图,∠1=∠2,则下列结论正确的是( )
(A)AD//BC (B)AB//CD
(C)AD//EF (D)EF//BC
C
3.如图,哪些条件能判定直线AB∥CD
1
4
3
2
A
D
C
B
能力挑战
4.如图:可以确定AB∥CE的条件是( )
A.∠2=∠B
B. ∠1=∠A
C. ∠3=∠B
D. ∠3=∠A
A E
B C D
1
2
3
C
能力挑战
(1)从∠1=∠2,可以推出 ∥ ,
理由是 .
(2)从∠2=∠ ,可以推出c∥d ,
理由是 .
(3)如果∠1=75°,∠4=105°,
可以推出 ∥ .
理由是 .
练一练
b
a
内错角相等,两直线平行
同位角相等,两直线平行
3
a
b
4
c
2
d
3
1
a
b
同旁内角互补,两直线平行
1.如图
从∠1=∠4,可以推出 ∥ ,
理由是 .
(2)从∠ABC +∠ =180,可以推出AB∥CD ,
理由是 .
(3)从∠ =∠ ,可以推出AD∥BC,
理由是 .
A
B
C
D
1
2
3
4
5
(4)从∠5=∠ ,可以推出AB∥CD,
理由是 .
AB
内错角相等,两直线平行
CD
BCD
同旁内角互补,两直线平行
2
3
内错角相等,两直线平行
ABC
同位角相等,两直线平行
2.如图
平行线判定方法1:同位角相等,两直线平行。
平行线判定方法2:内错角相等,两直线平行。
平行线判定方法2:同旁内角互补,两直线平行。
