2021-2022学年安徽省阜阳市阜南县九年级(上)质检数学试卷(12月份)(Word版 含解析)
文档属性
| 名称 | 2021-2022学年安徽省阜阳市阜南县九年级(上)质检数学试卷(12月份)(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-04 14:23:59 | ||
图片预览


文档简介
2021-2022学年安徽省阜阳市阜南县九年级第一学期质检数学试卷(12月份)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列图形一定是相似图形的是( )
A.两个矩形 B.两个等腰三角形
C.两个直角三角形 D.两个正方形
2.关于反比例函数y=,下列说法正确的是( )
A.函数图象经过点(1,3)
B.函数图象位于第一、三象限
C.当x>0时,y随x的增大而增大
D.当1<x<3时,1<y<3
3.如果m:n=1:2,那么下列各式中不成立的是( )
A. B. C. D.
4.已知在Rt△ABC中,∠C=90°,∠A=60°,则tanB的值为( )
A. B.1 C. D.2
5.某公司的生产利润原来是a元,经过连续两年的增长达到了y万元,如果每年增长的百分数都是x,那么y与x的函数关系是( )
A.y=x2+a B.y=a(x﹣1)2 C.y=a(1﹣x)2 D.y=a(1+x)2
6.如图四个图中,△ABC均与△A′B′C′相似,且对应点交于一点,则△ABC与△A′B′C′成位似图形的有( )
A.1个 B.2个 C.3个 D.4个
7.如图所示,九(二)班的同学准备在坡角为α的河堤上栽树,要求相邻两棵树之间的水平距离为8m,那么这两棵树在坡面上的距离AB为( )
A.8cosαm B.m C.8sinαm D.m
8.已知二次函数y=x2﹣4x+m的图象与x轴的交点坐标分别为x1、x2,若x1+3x2=6,则m的值为( )
A.3 B.﹣3 C.2 D.﹣2
9.如图,在平行四边形ABCD中,点E在边DC上,EC:DE=1:3,连接AE交BD于点F,则△DEF的面积与四边形BFEC的面积之比为( )
A.1:2 B.3:4 C.8:17 D.9:19
10.下列关于二次函数y=﹣(x﹣n)2+n2+1(n为常数)的结论:①该函数图象开口向下;②该函数的图象一定经过坐标轴上某个定点;③该函数图象的顶点在函数y=x2+1的图象上;④当0≤x≤1时,若该函数有最大值2,则n=±1.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共4小题,每小题5分,满分20分)
11.将抛物线y=2x2﹣12x+19向左平移2个单位长度后的解析式为 .
12.某一时刻,身高为1.5m的小明在阳光下的影长是0.3m,同一时刻同一地点测得某旗杆的影长是4m,那么该旗杆的高度是 m.
13.如图,点M是函数y=x与y=的图象在第一象限内的交点,OM=8,则k的值为 .
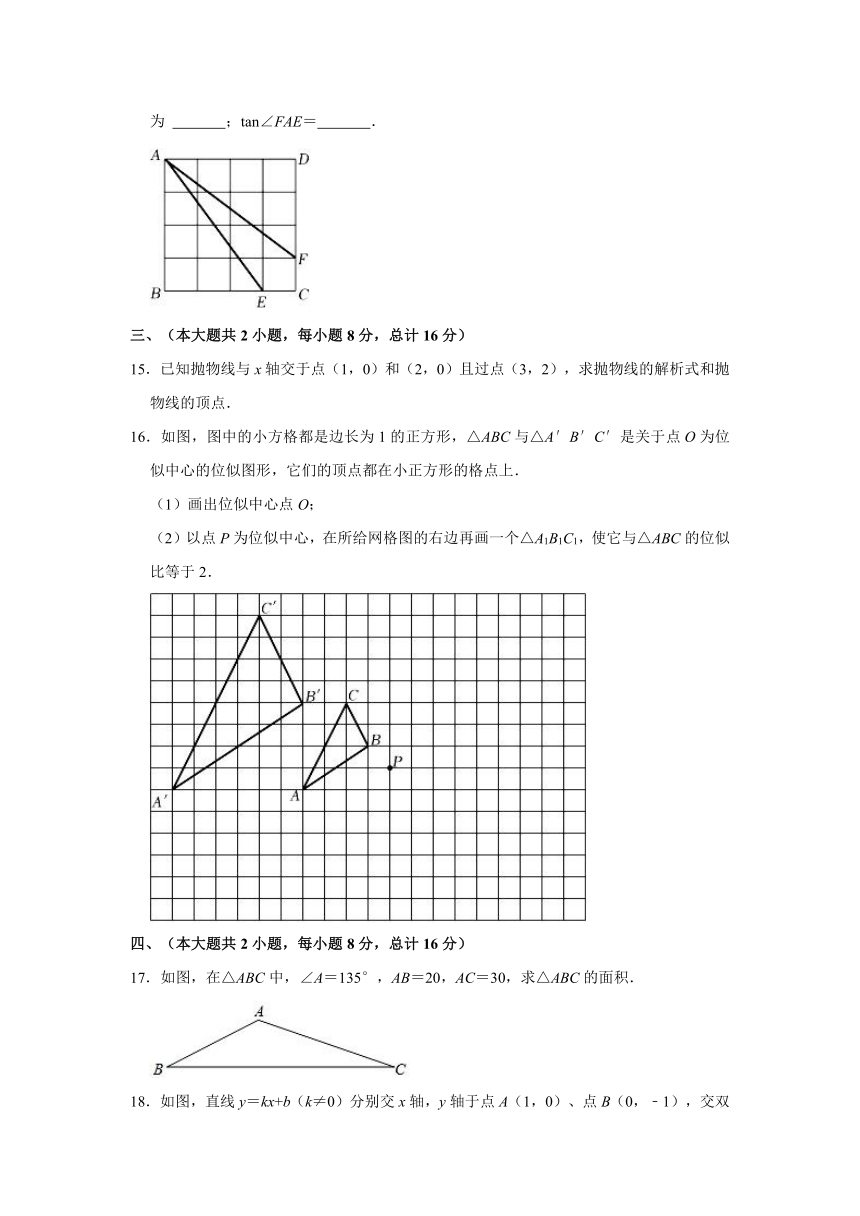
14.如图所示为4×4的网格,每个小正方形的边长均为1,则四边形AECF的面积为 ;tan∠FAE= .
三、(本大题共2小题,每小题8分,总计16分)
15.已知抛物线与x轴交于点(1,0)和(2,0)且过点(3,2),求抛物线的解析式和抛物线的顶点.
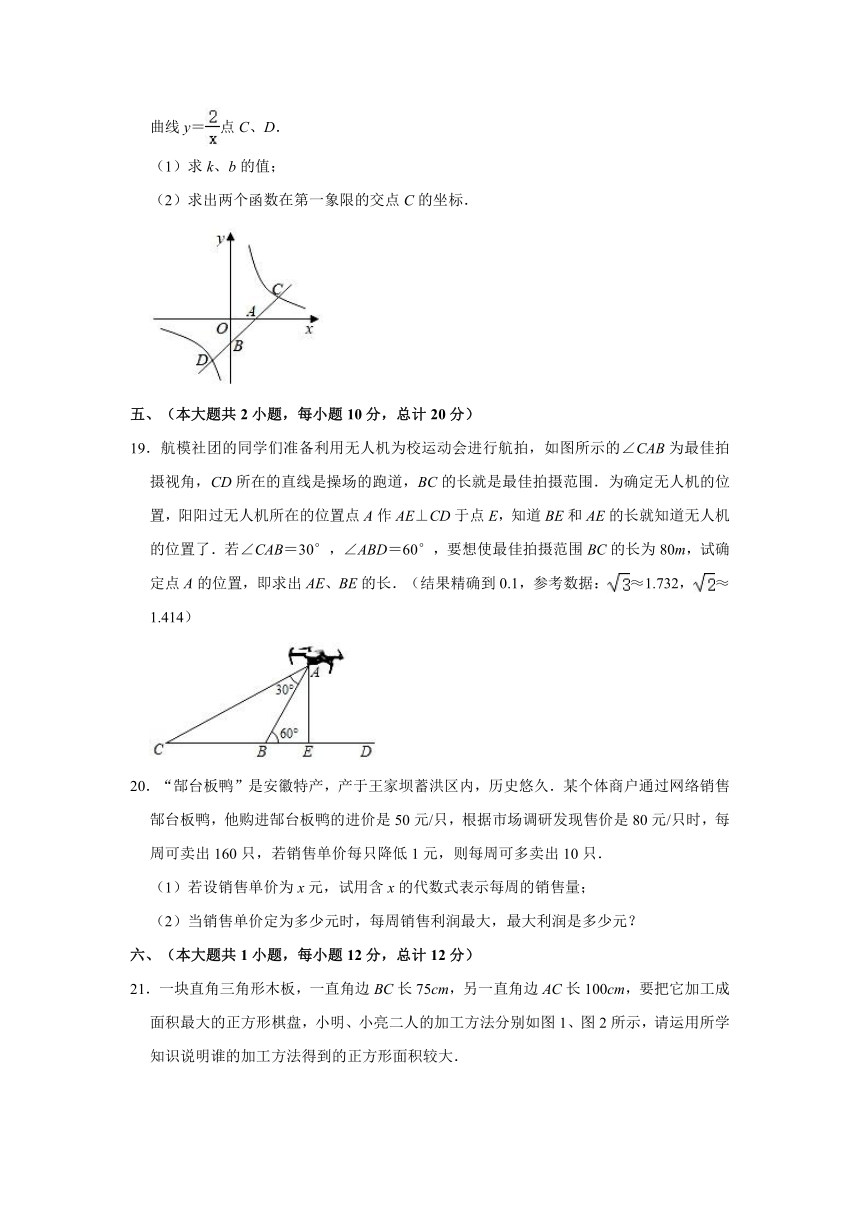
16.如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是关于点O为位似中心的位似图形,它们的顶点都在小正方形的格点上.
(1)画出位似中心点O;
(2)以点P为位似中心,在所给网格图的右边再画一个△A1B1C1,使它与△ABC的位似比等于2.
四、(本大题共2小题,每小题8分,总计16分)
17.如图,在△ABC中,∠A=135°,AB=20,AC=30,求△ABC的面积.
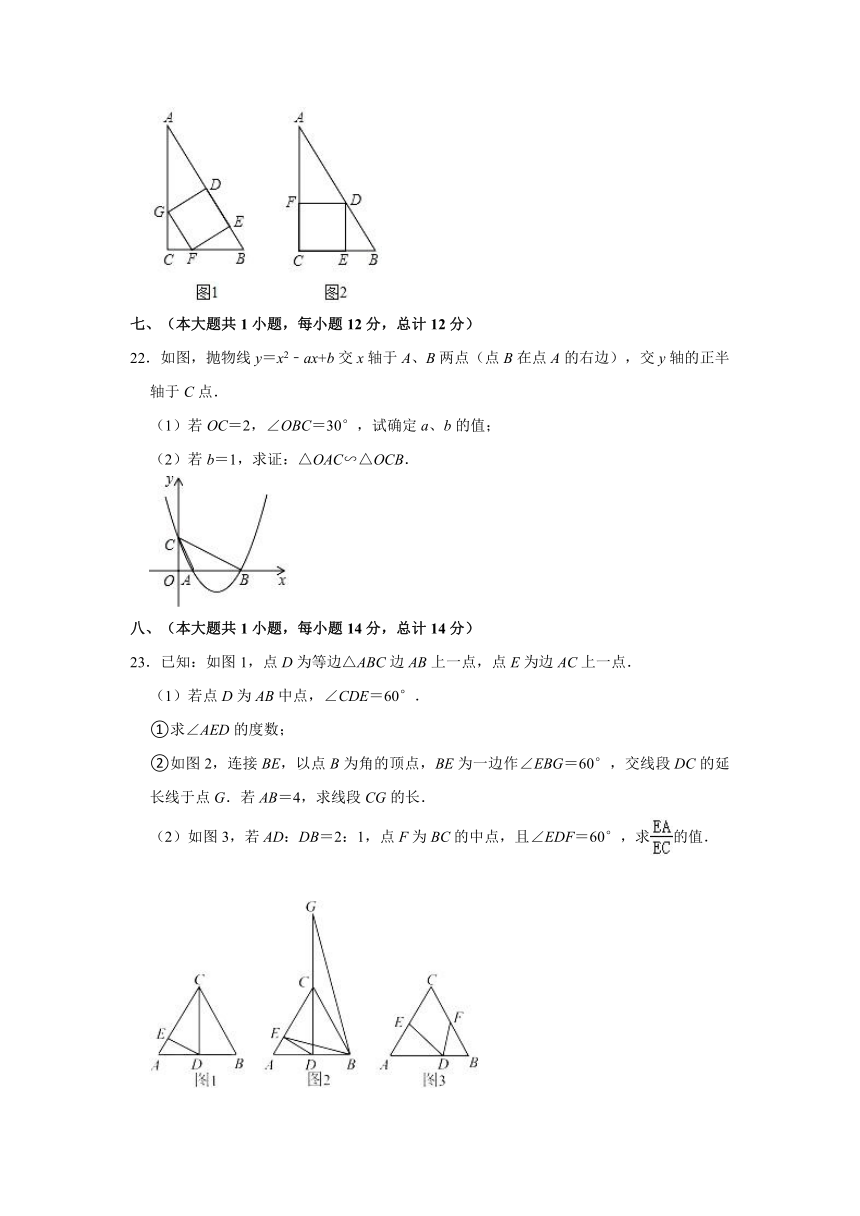
18.如图,直线y=kx+b(k≠0)分别交x轴,y轴于点A(1,0)、点B(0,﹣1),交双曲线y=点C、D.
(1)求k、b的值;
(2)求出两个函数在第一象限的交点C的坐标.
五、(本大题共2小题,每小题10分,总计20分)
19.航模社团的同学们准备利用无人机为校运动会进行航拍,如图所示的∠CAB为最佳拍摄视角,CD所在的直线是操场的跑道,BC的长就是最佳拍摄范围.为确定无人机的位置,阳阳过无人机所在的位置点A作AE⊥CD于点E,知道BE和AE的长就知道无人机的位置了.若∠CAB=30°,∠ABD=60°,要想使最佳拍摄范围BC的长为80m,试确定点A的位置,即求出AE、BE的长.(结果精确到0.1,参考数据:≈1.732,≈1.414)
20.“郜台板鸭”是安徽特产,产于王家坝蓄洪区内,历史悠久.某个体商户通过网络销售郜台板鸭,他购进郜台板鸭的进价是50元/只,根据市场调研发现售价是80元/只时,每周可卖出160只,若销售单价每只降低1元,则每周可多卖出10只.
(1)若设销售单价为x元,试用含x的代数式表示每周的销售量;
(2)当销售单价定为多少元时,每周销售利润最大,最大利润是多少元?
六、(本大题共1小题,每小题12分,总计12分)
21.一块直角三角形木板,一直角边BC长75cm,另一直角边AC长100cm,要把它加工成面积最大的正方形棋盘,小明、小亮二人的加工方法分别如图1、图2所示,请运用所学知识说明谁的加工方法得到的正方形面积较大.
七、(本大题共1小题,每小题12分,总计12分)
22.如图,抛物线y=x2﹣ax+b交x轴于A、B两点(点B在点A的右边),交y轴的正半轴于C点.
(1)若OC=2,∠OBC=30°,试确定a、b的值;
(2)若b=1,求证:△OAC∽△OCB.
八、(本大题共1小题,每小题14分,总计14分)
23.已知:如图1,点D为等边△ABC边AB上一点,点E为边AC上一点.
(1)若点D为AB中点,∠CDE=60°.
①求∠AED的度数;
②如图2,连接BE,以点B为角的顶点,BE为一边作∠EBG=60°,交线段DC的延长线于点G.若AB=4,求线段CG的长.
(2)如图3,若AD:DB=2:1,点F为BC的中点,且∠EDF=60°,求的值.
参考答案
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列图形一定是相似图形的是( )
A.两个矩形 B.两个等腰三角形
C.两个直角三角形 D.两个正方形
【分析】根据相似图形的定义,结合选项,用排除法求解.
解:A、两个矩形,对应角相等,对应边不一定成比例,故不符合题意;
B、两个等腰三角形顶角不一定相等,故不符合题意.
C、两个直角三角形,只有一个直角相同,锐角不一定相等,故不符合题意;
D、两个正方形,形状相同,大小不一定相同,符合相似性定义,故符合题意;
故选:D.
2.关于反比例函数y=,下列说法正确的是( )
A.函数图象经过点(1,3)
B.函数图象位于第一、三象限
C.当x>0时,y随x的增大而增大
D.当1<x<3时,1<y<3
【分析】利用反比例函数的性质解答.
解:根据函数的定义可知对于函数y=,是一个y关于x的反比例函数,
∵k=﹣3<0,函数图象位于第二、四象限,
∴1×3=3≠﹣3,
∴函数图象不经过点(1,3),
∴根据反比例函数的性质在函数图象的每一个象限内,y随x的增大而增大,当1<x<3时,3<y<1,
∴说法正确的是当x>0时,y随x的增大而增大,
故选:C.
3.如果m:n=1:2,那么下列各式中不成立的是( )
A. B. C. D.
【分析】根据比例式的性质得出x,y的关系,分别代入四个选项即可得出答案,也可用特殊值法求出.
解:∵m:n=1:2,
∴=,
A.当m=2,b=4时,==,故此选项错误;
B,,故本选项正确;
C,===2,故本选项正确;
D,,故本选项正确;
故选:A.
4.已知在Rt△ABC中,∠C=90°,∠A=60°,则tanB的值为( )
A. B.1 C. D.2
【分析】画出相应的图形,根据勾股定理和锐角三角函数的意义求解后,再做出判断即可.
解:如图,
∵∠C=90°,∠A=60°,
∴∠B=30°,
∴AB=2AC
∴BC==AC
∴tanB==,
故选:A.
5.某公司的生产利润原来是a元,经过连续两年的增长达到了y万元,如果每年增长的百分数都是x,那么y与x的函数关系是( )
A.y=x2+a B.y=a(x﹣1)2 C.y=a(1﹣x)2 D.y=a(1+x)2
【分析】本题是增长率的问题,基数是a元,增长次数2次,结果为y,根据增长率的公式表示函数关系式.
解:依题意,
得y=a(1+x)2.
故选:D.
6.如图四个图中,△ABC均与△A′B′C′相似,且对应点交于一点,则△ABC与△A′B′C′成位似图形的有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据位似图形的概念判断即可.
解:图1、图3、图4是位似图形,
图2的对应边不平行,不是位似图形,
故选:C.
7.如图所示,九(二)班的同学准备在坡角为α的河堤上栽树,要求相邻两棵树之间的水平距离为8m,那么这两棵树在坡面上的距离AB为( )
A.8cosαm B.m C.8sinαm D.m
【分析】直接利用锐角三角函数关系得出cosα=,进而得出答案.
解:由题意可得:cosα=,
则AB=.
故选:B.
8.已知二次函数y=x2﹣4x+m的图象与x轴的交点坐标分别为x1、x2,若x1+3x2=6,则m的值为( )
A.3 B.﹣3 C.2 D.﹣2
【分析】先将函数与x轴的交点求解转化为一元二次方程中根与系数的关系得到x1+x2的值,然后结合x1+3x2=6求得x1和x2的值,最后求得m的值.
解:由题意得,x1+x2=4,x1 x2=m,
∵x1+3x2=6,
∴x2=1,x1=3,
∴m=1×3=3,
故选:A.
9.如图,在平行四边形ABCD中,点E在边DC上,EC:DE=1:3,连接AE交BD于点F,则△DEF的面积与四边形BFEC的面积之比为( )
A.1:2 B.3:4 C.8:17 D.9:19
【分析】由EC:DE=1:3,可得DF:FB=3:4,根据在高相等的情况下三角形面积比等于底边的比,可得S△EFD:S△BEF=3:4,S△BDE:S△BEC=3:1,进而可求△DEF的面积与四边形BCEF的面积的比值.
解:连接BE
∵EC:DE=1:3,
∴设DE=3k,EC=k,
则CD=4k,
∵ABCD是平行四边形,
∴AB∥CD,AB=CD=4k,
∴△DEF∽△BAF,
∴==,
∴S△EFD:S△BEF=3:4,
∵EC:DE=1:3,
∴S△BDE:S△BEC=3:1,
设S△EFD=3a,则S△BEF=4a,
∴S△BDE=7a,S△BEC=a,
∴S四边形BCEF=S△BEC+S△BEF=a+4a=a,
∴△DEF的面积与四边形BCEF的面积之比为:3a:=9:19,
故选:D.
10.下列关于二次函数y=﹣(x﹣n)2+n2+1(n为常数)的结论:①该函数图象开口向下;②该函数的图象一定经过坐标轴上某个定点;③该函数图象的顶点在函数y=x2+1的图象上;④当0≤x≤1时,若该函数有最大值2,则n=±1.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
【分析】利用二次函数的性质一一判断即可.
解:①∵二次函数y=﹣(x﹣n)2+n2+1(n为常数)中a=﹣1<0,
∴该函数图象开口向下,故结论①正确;
②∵在函数y=﹣(x﹣n)2+n2+1中,令x=0,则y=﹣n2+n2+1=1,
∴该函数的图象一定经过点(0,1),故结论②正确;
③∵抛物线开口向下,当x=n时,函数y有最大值n2+1,
∴该函数的图象的顶点在函数y=x2+1的图象上.故结论③正确;
④∵y=﹣(x﹣n)2+n2+1,
∴对称轴为直线x=n,当x≤n时,y随x的增大而增大,
∴当0≤x≤1时,若该函数有最大值2,则n=1,故结论④错误;
∴正确结论有3个,
故选:C.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.将抛物线y=2x2﹣12x+19向左平移2个单位长度后的解析式为 y=2(x﹣1)2+2 .
【分析】根据“上加下减,左加右减”的原则进行解答即可.
解:∵y=2x2﹣12x+19=2(x﹣3)2+1,
∴将抛物线y=2x2﹣12x+19向左平移2个单位长度后的解析式为:y=2(x﹣3+2)2+1,即y=2(x﹣1)2+21
故答案为:y=2(x﹣1)2+1.
12.某一时刻,身高为1.5m的小明在阳光下的影长是0.3m,同一时刻同一地点测得某旗杆的影长是4m,那么该旗杆的高度是 20 m.
【分析】设该旗杆的高度为xm,根据三角形相似的性质得到同一时刻同一地点物体的高度与其影长的比相等,即有1.5:0.3=x:4,然后解方程即可.
解:设该旗杆的高度为xm,
根据题意,得1.5:0.3=x:4,
解得x=20.
即该旗杆的高度是20m.
故答案为:20.
13.如图,点M是函数y=x与y=的图象在第一象限内的交点,OM=8,则k的值为 16 .
【分析】设点M的坐标为:(m,m),根据OM=8,结合勾股定理,得到关于m的一元二次方程,解之,得到点M的坐标,代入y=,即可得到答案.
解:设点M的坐标为:(m,m),则m>0,
根据题意得:m2+(m)2=82,
解得:m=4,
即点M的坐标为:(4,4),
把点M(4,4)代入y=得:
k=4×4=16,
故答案为:16.
14.如图所示为4×4的网格,每个小正方形的边长均为1,则四边形AECF的面积为 4 ;tan∠FAE= .
【分析】连接EF,过点F作FG⊥AE,垂足为G.利用正方形的面积﹣两个直角三角形的面积计算出四边形的面积;先计算△AEF的面积,再利用面积和勾股定理求出FG、AG,最后求出∠FAE的正切值.
解:连接EF,过点F作FG⊥AE,垂足为G.
S四边形AECF=S正方形ABCD﹣S△ABE﹣S△ADF
=4×4﹣×4×3﹣×4×3
=16﹣6﹣6
=4;
S△AEF=S四边形AECF﹣S△CEF
=4﹣
=.
∵AE=AF==5,
∴AE FG=.
∴FG=.
∴AG=
=
=.
∴tan∠FAE===.
故答案为:4,.
三、(本大题共2小题,每小题8分,总计16分)
15.已知抛物线与x轴交于点(1,0)和(2,0)且过点(3,2),求抛物线的解析式和抛物线的顶点.
【分析】由题意设二次函数的交点式,然后用待定系数法求解析式,再转化为顶点式求得顶点坐标.
解:∵抛物线与x轴交于点(1,0)和(2,0)且过点(3,2),
设y=a(x﹣1)(x﹣2),则
2=a(3﹣1)×(3﹣2),
∴a=1,
∴y=(x﹣1)(x﹣2)=x2﹣3x+2=(x﹣)2﹣,
∴抛物线的顶点坐标为(,﹣),解析式为y=x2﹣3x+2.
16.如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是关于点O为位似中心的位似图形,它们的顶点都在小正方形的格点上.
(1)画出位似中心点O;
(2)以点P为位似中心,在所给网格图的右边再画一个△A1B1C1,使它与△ABC的位似比等于2.
【分析】(1)分别延长A′A、B′B和C′C,它们的交点即为O点;
(2)延长AP到A1,使A1P=2PA,延长BP到B1,使B1P=2PB,延长CP到C1,使C1P=2PC,则△A1B1C1使它满足条件.
解:(1)如图,点O为所作;
(2)如图,△A1B1C1为所作.
四、(本大题共2小题,每小题8分,总计16分)
17.如图,在△ABC中,∠A=135°,AB=20,AC=30,求△ABC的面积.
【分析】过点B作BE⊥AC,根据勾股定理可求得BE,再根据三角形的面积公式求出答案.
解:过点B作BE⊥AC,
∵∠A=135°,
∴∠BAE=180°﹣∠A=180°﹣135°=45°,
∴∠ABE=90°﹣∠BAE=90°﹣45°=45°,
在Rt△BAE中,BE2+AE2=AB2,
∵AB=20,
∴BE==10,
∵AC=30,
∴S△ABC=AC BE=×30×10=150.
18.如图,直线y=kx+b(k≠0)分别交x轴,y轴于点A(1,0)、点B(0,﹣1),交双曲线y=点C、D.
(1)求k、b的值;
(2)求出两个函数在第一象限的交点C的坐标.
【分析】(1)把A、B的坐标代入一次函数的解析式,即可求出k、b;
(2)解由两函数组成的方程组,求出方程组的解即可得出C、D的坐标;由此可得出点C的坐标即可得出答案.
解:(1)∵直线y=kx+b过点(1,0)和(0,﹣1),
∴,
∴k=1,b=﹣1;
(2)联立,得或,
∴C(2,1).
五、(本大题共2小题,每小题10分,总计20分)
19.航模社团的同学们准备利用无人机为校运动会进行航拍,如图所示的∠CAB为最佳拍摄视角,CD所在的直线是操场的跑道,BC的长就是最佳拍摄范围.为确定无人机的位置,阳阳过无人机所在的位置点A作AE⊥CD于点E,知道BE和AE的长就知道无人机的位置了.若∠CAB=30°,∠ABD=60°,要想使最佳拍摄范围BC的长为80m,试确定点A的位置,即求出AE、BE的长.(结果精确到0.1,参考数据:≈1.732,≈1.414)
【分析】根据含30度角的直角三角形的性质即可解决问题.
解:∵AE⊥CD,
∴∠AEB=90°,
∵∠CAB=30°,∠ABD=60°,
∴∠C=30°,
∴AB=BC=80m,
∴BE=AB=40m,
∴AE=BE=40≈69.3(m),
答:AE、BE的长分别为69.3m、40m.
20.“郜台板鸭”是安徽特产,产于王家坝蓄洪区内,历史悠久.某个体商户通过网络销售郜台板鸭,他购进郜台板鸭的进价是50元/只,根据市场调研发现售价是80元/只时,每周可卖出160只,若销售单价每只降低1元,则每周可多卖出10只.
(1)若设销售单价为x元,试用含x的代数式表示每周的销售量;
(2)当销售单价定为多少元时,每周销售利润最大,最大利润是多少元?
【分析】(1)根据题意,由售价是80元/个时,每周可卖出160只,若销售单价每个降低1元,则每周可多卖出10个,可得结论;
(2)根据题意结合每周获得的利润w=销量×每只的利润,进而利用二次函数增减性求出答案只
解:(1)由题意得每周的销售量为:160﹣10(x﹣80)=(﹣10x+960)只;
(2)设每周的销售利润为w元,根据题意得:
w=(x﹣50)(﹣10x+960)
=﹣10x2+1460x﹣48000
=﹣10(x﹣72)2+3840,
∵﹣10<0,
∴当x=72时,w有最大值,最大值为3840,
∴当销售单价定为72元时,每周销售利润最大,最大利润是3840元.
六、(本大题共1小题,每小题12分,总计12分)
21.一块直角三角形木板,一直角边BC长75cm,另一直角边AC长100cm,要把它加工成面积最大的正方形棋盘,小明、小亮二人的加工方法分别如图1、图2所示,请运用所学知识说明谁的加工方法得到的正方形面积较大.
【分析】根据相似三角形的性质,相似三角形的对应边成比例求出两个图形中正方形的边长,则可得出答案.
解:设图1加工桌面长xcm,过点C作CM⊥AB,垂足为M,与GF相交于点N,
∵BC=75cm,AC=100cm,
∴BA===125(cm),
∵S△ACB=AB MC,
∴CM===60(cm),
∵GF∥DE,
∴△CGF∽△CAB,
∴,
∴.
∴.
∴x=;
设图2加工桌面长ycm,
∵FD∥BC,
∴Rt△AFD∽Rt△ACB,
∴,
,
解得y=,
∵,
∴图2加工方法得到的正方形面积较大.
七、(本大题共1小题,每小题12分,总计12分)
22.如图,抛物线y=x2﹣ax+b交x轴于A、B两点(点B在点A的右边),交y轴的正半轴于C点.
(1)若OC=2,∠OBC=30°,试确定a、b的值;
(2)若b=1,求证:△OAC∽△OCB.
【分析】(1)根据OC=2可以得到C(0,2);然后通过解直角△OBC求得线段OB=2,则B(0,2),将其代入函数解析式求得a的值即可;
(2)欲证明△OAC∽△OCB,只需推知=即可.
【解答】(1)解:∵OC=2,∠OBC=30°,
∴OB===2.
∴B(2,0),C(0,2),
∴.
解得;
(2)证明:当b=1时,该抛物线解析式是y=x2﹣ax+1.
当x=0时,y=1,即C(0,1),此时OC=1.
设点A、B的横坐标分别是x1、x2,
令y=0,则x2﹣ax+1=0.
由根与系数的关系得到:x1 x2=1,即OA OB=1,
∴OA=.
∴=.
∵OC=1,
∴=.
又∵∠COA=∠BOC,
∴△OAC∽△OCB.
八、(本大题共1小题,每小题14分,总计14分)
23.已知:如图1,点D为等边△ABC边AB上一点,点E为边AC上一点.
(1)若点D为AB中点,∠CDE=60°.
①求∠AED的度数;
②如图2,连接BE,以点B为角的顶点,BE为一边作∠EBG=60°,交线段DC的延长线于点G.若AB=4,求线段CG的长.
(2)如图3,若AD:DB=2:1,点F为BC的中点,且∠EDF=60°,求的值.
【分析】(1)①根据△ABC是等边三角形三线合一的性质可得∠ACD=ACB=30°,进而可以解决问题;
②根据等边三角形的性质可得∠ADE=30°,然后根据含30度角的直角三角形求出DE的长,证明△BDE∽△BCG,对应边成比例即可解决问题;
(2)证明△AED∽△BDF,可得=,根据AD:DB=2:1,可得BD=AB,AD=AB,根据点F为BC的中点,可得BF=BC=AB,进而可以解决问题.
解:(1)①∵△ABC是等边三角形,点D为AB中点,
∴∠ACD=ACB=30°,
∵∠CDE=60°.
∴∠AED=∠ACD+∠CDE=90°;
②∵△ABC是等边三角形,
∴AB=AC=4,∠A=∠ABC=∠ACB=60°,
∵点D为AB中点,
∴∠CDB=90°,AD=DB=AB=2,∠DCB=ACB=30°,
∵∠AED=90°,
∴∠ADE=30°,
∴AE=AD=1,
∴DE==,
∵∠EBG=∠EBC+∠CBG=60°,∠ABC=∠EBC+∠ABE=60°,
∴∠ABE=∠CBG,
∵∠BDE=∠CDE+∠CDB=60°+90°=150°,
∠BCG=180°﹣∠BCD=180°﹣30°=150°,
∴∠BDE=∠BCG,
∴△BDE∽△BCG,
∴=,
∴=,
∴CG=2;
(2)∵∠EDF=60°,
∴∠ADE+∠BDF=180°﹣∠EDF=120°,
∠ADE+∠AED=180°﹣∠A=120°,
∴∠AED=∠BDF,
∵∠A=∠B=60°,
∴△AED∽△BDF,
∴=,
∵AD:DB=2:1,
∴BD=AB,AD=AB,
∵点F为BC的中点,
∴BF=BC=AB,
∴=,
∴=,
∴=,
∴=.
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列图形一定是相似图形的是( )
A.两个矩形 B.两个等腰三角形
C.两个直角三角形 D.两个正方形
2.关于反比例函数y=,下列说法正确的是( )
A.函数图象经过点(1,3)
B.函数图象位于第一、三象限
C.当x>0时,y随x的增大而增大
D.当1<x<3时,1<y<3
3.如果m:n=1:2,那么下列各式中不成立的是( )
A. B. C. D.
4.已知在Rt△ABC中,∠C=90°,∠A=60°,则tanB的值为( )
A. B.1 C. D.2
5.某公司的生产利润原来是a元,经过连续两年的增长达到了y万元,如果每年增长的百分数都是x,那么y与x的函数关系是( )
A.y=x2+a B.y=a(x﹣1)2 C.y=a(1﹣x)2 D.y=a(1+x)2
6.如图四个图中,△ABC均与△A′B′C′相似,且对应点交于一点,则△ABC与△A′B′C′成位似图形的有( )
A.1个 B.2个 C.3个 D.4个
7.如图所示,九(二)班的同学准备在坡角为α的河堤上栽树,要求相邻两棵树之间的水平距离为8m,那么这两棵树在坡面上的距离AB为( )
A.8cosαm B.m C.8sinαm D.m
8.已知二次函数y=x2﹣4x+m的图象与x轴的交点坐标分别为x1、x2,若x1+3x2=6,则m的值为( )
A.3 B.﹣3 C.2 D.﹣2
9.如图,在平行四边形ABCD中,点E在边DC上,EC:DE=1:3,连接AE交BD于点F,则△DEF的面积与四边形BFEC的面积之比为( )
A.1:2 B.3:4 C.8:17 D.9:19
10.下列关于二次函数y=﹣(x﹣n)2+n2+1(n为常数)的结论:①该函数图象开口向下;②该函数的图象一定经过坐标轴上某个定点;③该函数图象的顶点在函数y=x2+1的图象上;④当0≤x≤1时,若该函数有最大值2,则n=±1.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共4小题,每小题5分,满分20分)
11.将抛物线y=2x2﹣12x+19向左平移2个单位长度后的解析式为 .
12.某一时刻,身高为1.5m的小明在阳光下的影长是0.3m,同一时刻同一地点测得某旗杆的影长是4m,那么该旗杆的高度是 m.
13.如图,点M是函数y=x与y=的图象在第一象限内的交点,OM=8,则k的值为 .
14.如图所示为4×4的网格,每个小正方形的边长均为1,则四边形AECF的面积为 ;tan∠FAE= .
三、(本大题共2小题,每小题8分,总计16分)
15.已知抛物线与x轴交于点(1,0)和(2,0)且过点(3,2),求抛物线的解析式和抛物线的顶点.
16.如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是关于点O为位似中心的位似图形,它们的顶点都在小正方形的格点上.
(1)画出位似中心点O;
(2)以点P为位似中心,在所给网格图的右边再画一个△A1B1C1,使它与△ABC的位似比等于2.
四、(本大题共2小题,每小题8分,总计16分)
17.如图,在△ABC中,∠A=135°,AB=20,AC=30,求△ABC的面积.
18.如图,直线y=kx+b(k≠0)分别交x轴,y轴于点A(1,0)、点B(0,﹣1),交双曲线y=点C、D.
(1)求k、b的值;
(2)求出两个函数在第一象限的交点C的坐标.
五、(本大题共2小题,每小题10分,总计20分)
19.航模社团的同学们准备利用无人机为校运动会进行航拍,如图所示的∠CAB为最佳拍摄视角,CD所在的直线是操场的跑道,BC的长就是最佳拍摄范围.为确定无人机的位置,阳阳过无人机所在的位置点A作AE⊥CD于点E,知道BE和AE的长就知道无人机的位置了.若∠CAB=30°,∠ABD=60°,要想使最佳拍摄范围BC的长为80m,试确定点A的位置,即求出AE、BE的长.(结果精确到0.1,参考数据:≈1.732,≈1.414)
20.“郜台板鸭”是安徽特产,产于王家坝蓄洪区内,历史悠久.某个体商户通过网络销售郜台板鸭,他购进郜台板鸭的进价是50元/只,根据市场调研发现售价是80元/只时,每周可卖出160只,若销售单价每只降低1元,则每周可多卖出10只.
(1)若设销售单价为x元,试用含x的代数式表示每周的销售量;
(2)当销售单价定为多少元时,每周销售利润最大,最大利润是多少元?
六、(本大题共1小题,每小题12分,总计12分)
21.一块直角三角形木板,一直角边BC长75cm,另一直角边AC长100cm,要把它加工成面积最大的正方形棋盘,小明、小亮二人的加工方法分别如图1、图2所示,请运用所学知识说明谁的加工方法得到的正方形面积较大.
七、(本大题共1小题,每小题12分,总计12分)
22.如图,抛物线y=x2﹣ax+b交x轴于A、B两点(点B在点A的右边),交y轴的正半轴于C点.
(1)若OC=2,∠OBC=30°,试确定a、b的值;
(2)若b=1,求证:△OAC∽△OCB.
八、(本大题共1小题,每小题14分,总计14分)
23.已知:如图1,点D为等边△ABC边AB上一点,点E为边AC上一点.
(1)若点D为AB中点,∠CDE=60°.
①求∠AED的度数;
②如图2,连接BE,以点B为角的顶点,BE为一边作∠EBG=60°,交线段DC的延长线于点G.若AB=4,求线段CG的长.
(2)如图3,若AD:DB=2:1,点F为BC的中点,且∠EDF=60°,求的值.
参考答案
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列图形一定是相似图形的是( )
A.两个矩形 B.两个等腰三角形
C.两个直角三角形 D.两个正方形
【分析】根据相似图形的定义,结合选项,用排除法求解.
解:A、两个矩形,对应角相等,对应边不一定成比例,故不符合题意;
B、两个等腰三角形顶角不一定相等,故不符合题意.
C、两个直角三角形,只有一个直角相同,锐角不一定相等,故不符合题意;
D、两个正方形,形状相同,大小不一定相同,符合相似性定义,故符合题意;
故选:D.
2.关于反比例函数y=,下列说法正确的是( )
A.函数图象经过点(1,3)
B.函数图象位于第一、三象限
C.当x>0时,y随x的增大而增大
D.当1<x<3时,1<y<3
【分析】利用反比例函数的性质解答.
解:根据函数的定义可知对于函数y=,是一个y关于x的反比例函数,
∵k=﹣3<0,函数图象位于第二、四象限,
∴1×3=3≠﹣3,
∴函数图象不经过点(1,3),
∴根据反比例函数的性质在函数图象的每一个象限内,y随x的增大而增大,当1<x<3时,3<y<1,
∴说法正确的是当x>0时,y随x的增大而增大,
故选:C.
3.如果m:n=1:2,那么下列各式中不成立的是( )
A. B. C. D.
【分析】根据比例式的性质得出x,y的关系,分别代入四个选项即可得出答案,也可用特殊值法求出.
解:∵m:n=1:2,
∴=,
A.当m=2,b=4时,==,故此选项错误;
B,,故本选项正确;
C,===2,故本选项正确;
D,,故本选项正确;
故选:A.
4.已知在Rt△ABC中,∠C=90°,∠A=60°,则tanB的值为( )
A. B.1 C. D.2
【分析】画出相应的图形,根据勾股定理和锐角三角函数的意义求解后,再做出判断即可.
解:如图,
∵∠C=90°,∠A=60°,
∴∠B=30°,
∴AB=2AC
∴BC==AC
∴tanB==,
故选:A.
5.某公司的生产利润原来是a元,经过连续两年的增长达到了y万元,如果每年增长的百分数都是x,那么y与x的函数关系是( )
A.y=x2+a B.y=a(x﹣1)2 C.y=a(1﹣x)2 D.y=a(1+x)2
【分析】本题是增长率的问题,基数是a元,增长次数2次,结果为y,根据增长率的公式表示函数关系式.
解:依题意,
得y=a(1+x)2.
故选:D.
6.如图四个图中,△ABC均与△A′B′C′相似,且对应点交于一点,则△ABC与△A′B′C′成位似图形的有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据位似图形的概念判断即可.
解:图1、图3、图4是位似图形,
图2的对应边不平行,不是位似图形,
故选:C.
7.如图所示,九(二)班的同学准备在坡角为α的河堤上栽树,要求相邻两棵树之间的水平距离为8m,那么这两棵树在坡面上的距离AB为( )
A.8cosαm B.m C.8sinαm D.m
【分析】直接利用锐角三角函数关系得出cosα=,进而得出答案.
解:由题意可得:cosα=,
则AB=.
故选:B.
8.已知二次函数y=x2﹣4x+m的图象与x轴的交点坐标分别为x1、x2,若x1+3x2=6,则m的值为( )
A.3 B.﹣3 C.2 D.﹣2
【分析】先将函数与x轴的交点求解转化为一元二次方程中根与系数的关系得到x1+x2的值,然后结合x1+3x2=6求得x1和x2的值,最后求得m的值.
解:由题意得,x1+x2=4,x1 x2=m,
∵x1+3x2=6,
∴x2=1,x1=3,
∴m=1×3=3,
故选:A.
9.如图,在平行四边形ABCD中,点E在边DC上,EC:DE=1:3,连接AE交BD于点F,则△DEF的面积与四边形BFEC的面积之比为( )
A.1:2 B.3:4 C.8:17 D.9:19
【分析】由EC:DE=1:3,可得DF:FB=3:4,根据在高相等的情况下三角形面积比等于底边的比,可得S△EFD:S△BEF=3:4,S△BDE:S△BEC=3:1,进而可求△DEF的面积与四边形BCEF的面积的比值.
解:连接BE
∵EC:DE=1:3,
∴设DE=3k,EC=k,
则CD=4k,
∵ABCD是平行四边形,
∴AB∥CD,AB=CD=4k,
∴△DEF∽△BAF,
∴==,
∴S△EFD:S△BEF=3:4,
∵EC:DE=1:3,
∴S△BDE:S△BEC=3:1,
设S△EFD=3a,则S△BEF=4a,
∴S△BDE=7a,S△BEC=a,
∴S四边形BCEF=S△BEC+S△BEF=a+4a=a,
∴△DEF的面积与四边形BCEF的面积之比为:3a:=9:19,
故选:D.
10.下列关于二次函数y=﹣(x﹣n)2+n2+1(n为常数)的结论:①该函数图象开口向下;②该函数的图象一定经过坐标轴上某个定点;③该函数图象的顶点在函数y=x2+1的图象上;④当0≤x≤1时,若该函数有最大值2,则n=±1.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
【分析】利用二次函数的性质一一判断即可.
解:①∵二次函数y=﹣(x﹣n)2+n2+1(n为常数)中a=﹣1<0,
∴该函数图象开口向下,故结论①正确;
②∵在函数y=﹣(x﹣n)2+n2+1中,令x=0,则y=﹣n2+n2+1=1,
∴该函数的图象一定经过点(0,1),故结论②正确;
③∵抛物线开口向下,当x=n时,函数y有最大值n2+1,
∴该函数的图象的顶点在函数y=x2+1的图象上.故结论③正确;
④∵y=﹣(x﹣n)2+n2+1,
∴对称轴为直线x=n,当x≤n时,y随x的增大而增大,
∴当0≤x≤1时,若该函数有最大值2,则n=1,故结论④错误;
∴正确结论有3个,
故选:C.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.将抛物线y=2x2﹣12x+19向左平移2个单位长度后的解析式为 y=2(x﹣1)2+2 .
【分析】根据“上加下减,左加右减”的原则进行解答即可.
解:∵y=2x2﹣12x+19=2(x﹣3)2+1,
∴将抛物线y=2x2﹣12x+19向左平移2个单位长度后的解析式为:y=2(x﹣3+2)2+1,即y=2(x﹣1)2+21
故答案为:y=2(x﹣1)2+1.
12.某一时刻,身高为1.5m的小明在阳光下的影长是0.3m,同一时刻同一地点测得某旗杆的影长是4m,那么该旗杆的高度是 20 m.
【分析】设该旗杆的高度为xm,根据三角形相似的性质得到同一时刻同一地点物体的高度与其影长的比相等,即有1.5:0.3=x:4,然后解方程即可.
解:设该旗杆的高度为xm,
根据题意,得1.5:0.3=x:4,
解得x=20.
即该旗杆的高度是20m.
故答案为:20.
13.如图,点M是函数y=x与y=的图象在第一象限内的交点,OM=8,则k的值为 16 .
【分析】设点M的坐标为:(m,m),根据OM=8,结合勾股定理,得到关于m的一元二次方程,解之,得到点M的坐标,代入y=,即可得到答案.
解:设点M的坐标为:(m,m),则m>0,
根据题意得:m2+(m)2=82,
解得:m=4,
即点M的坐标为:(4,4),
把点M(4,4)代入y=得:
k=4×4=16,
故答案为:16.
14.如图所示为4×4的网格,每个小正方形的边长均为1,则四边形AECF的面积为 4 ;tan∠FAE= .
【分析】连接EF,过点F作FG⊥AE,垂足为G.利用正方形的面积﹣两个直角三角形的面积计算出四边形的面积;先计算△AEF的面积,再利用面积和勾股定理求出FG、AG,最后求出∠FAE的正切值.
解:连接EF,过点F作FG⊥AE,垂足为G.
S四边形AECF=S正方形ABCD﹣S△ABE﹣S△ADF
=4×4﹣×4×3﹣×4×3
=16﹣6﹣6
=4;
S△AEF=S四边形AECF﹣S△CEF
=4﹣
=.
∵AE=AF==5,
∴AE FG=.
∴FG=.
∴AG=
=
=.
∴tan∠FAE===.
故答案为:4,.
三、(本大题共2小题,每小题8分,总计16分)
15.已知抛物线与x轴交于点(1,0)和(2,0)且过点(3,2),求抛物线的解析式和抛物线的顶点.
【分析】由题意设二次函数的交点式,然后用待定系数法求解析式,再转化为顶点式求得顶点坐标.
解:∵抛物线与x轴交于点(1,0)和(2,0)且过点(3,2),
设y=a(x﹣1)(x﹣2),则
2=a(3﹣1)×(3﹣2),
∴a=1,
∴y=(x﹣1)(x﹣2)=x2﹣3x+2=(x﹣)2﹣,
∴抛物线的顶点坐标为(,﹣),解析式为y=x2﹣3x+2.
16.如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是关于点O为位似中心的位似图形,它们的顶点都在小正方形的格点上.
(1)画出位似中心点O;
(2)以点P为位似中心,在所给网格图的右边再画一个△A1B1C1,使它与△ABC的位似比等于2.
【分析】(1)分别延长A′A、B′B和C′C,它们的交点即为O点;
(2)延长AP到A1,使A1P=2PA,延长BP到B1,使B1P=2PB,延长CP到C1,使C1P=2PC,则△A1B1C1使它满足条件.
解:(1)如图,点O为所作;
(2)如图,△A1B1C1为所作.
四、(本大题共2小题,每小题8分,总计16分)
17.如图,在△ABC中,∠A=135°,AB=20,AC=30,求△ABC的面积.
【分析】过点B作BE⊥AC,根据勾股定理可求得BE,再根据三角形的面积公式求出答案.
解:过点B作BE⊥AC,
∵∠A=135°,
∴∠BAE=180°﹣∠A=180°﹣135°=45°,
∴∠ABE=90°﹣∠BAE=90°﹣45°=45°,
在Rt△BAE中,BE2+AE2=AB2,
∵AB=20,
∴BE==10,
∵AC=30,
∴S△ABC=AC BE=×30×10=150.
18.如图,直线y=kx+b(k≠0)分别交x轴,y轴于点A(1,0)、点B(0,﹣1),交双曲线y=点C、D.
(1)求k、b的值;
(2)求出两个函数在第一象限的交点C的坐标.
【分析】(1)把A、B的坐标代入一次函数的解析式,即可求出k、b;
(2)解由两函数组成的方程组,求出方程组的解即可得出C、D的坐标;由此可得出点C的坐标即可得出答案.
解:(1)∵直线y=kx+b过点(1,0)和(0,﹣1),
∴,
∴k=1,b=﹣1;
(2)联立,得或,
∴C(2,1).
五、(本大题共2小题,每小题10分,总计20分)
19.航模社团的同学们准备利用无人机为校运动会进行航拍,如图所示的∠CAB为最佳拍摄视角,CD所在的直线是操场的跑道,BC的长就是最佳拍摄范围.为确定无人机的位置,阳阳过无人机所在的位置点A作AE⊥CD于点E,知道BE和AE的长就知道无人机的位置了.若∠CAB=30°,∠ABD=60°,要想使最佳拍摄范围BC的长为80m,试确定点A的位置,即求出AE、BE的长.(结果精确到0.1,参考数据:≈1.732,≈1.414)
【分析】根据含30度角的直角三角形的性质即可解决问题.
解:∵AE⊥CD,
∴∠AEB=90°,
∵∠CAB=30°,∠ABD=60°,
∴∠C=30°,
∴AB=BC=80m,
∴BE=AB=40m,
∴AE=BE=40≈69.3(m),
答:AE、BE的长分别为69.3m、40m.
20.“郜台板鸭”是安徽特产,产于王家坝蓄洪区内,历史悠久.某个体商户通过网络销售郜台板鸭,他购进郜台板鸭的进价是50元/只,根据市场调研发现售价是80元/只时,每周可卖出160只,若销售单价每只降低1元,则每周可多卖出10只.
(1)若设销售单价为x元,试用含x的代数式表示每周的销售量;
(2)当销售单价定为多少元时,每周销售利润最大,最大利润是多少元?
【分析】(1)根据题意,由售价是80元/个时,每周可卖出160只,若销售单价每个降低1元,则每周可多卖出10个,可得结论;
(2)根据题意结合每周获得的利润w=销量×每只的利润,进而利用二次函数增减性求出答案只
解:(1)由题意得每周的销售量为:160﹣10(x﹣80)=(﹣10x+960)只;
(2)设每周的销售利润为w元,根据题意得:
w=(x﹣50)(﹣10x+960)
=﹣10x2+1460x﹣48000
=﹣10(x﹣72)2+3840,
∵﹣10<0,
∴当x=72时,w有最大值,最大值为3840,
∴当销售单价定为72元时,每周销售利润最大,最大利润是3840元.
六、(本大题共1小题,每小题12分,总计12分)
21.一块直角三角形木板,一直角边BC长75cm,另一直角边AC长100cm,要把它加工成面积最大的正方形棋盘,小明、小亮二人的加工方法分别如图1、图2所示,请运用所学知识说明谁的加工方法得到的正方形面积较大.
【分析】根据相似三角形的性质,相似三角形的对应边成比例求出两个图形中正方形的边长,则可得出答案.
解:设图1加工桌面长xcm,过点C作CM⊥AB,垂足为M,与GF相交于点N,
∵BC=75cm,AC=100cm,
∴BA===125(cm),
∵S△ACB=AB MC,
∴CM===60(cm),
∵GF∥DE,
∴△CGF∽△CAB,
∴,
∴.
∴.
∴x=;
设图2加工桌面长ycm,
∵FD∥BC,
∴Rt△AFD∽Rt△ACB,
∴,
,
解得y=,
∵,
∴图2加工方法得到的正方形面积较大.
七、(本大题共1小题,每小题12分,总计12分)
22.如图,抛物线y=x2﹣ax+b交x轴于A、B两点(点B在点A的右边),交y轴的正半轴于C点.
(1)若OC=2,∠OBC=30°,试确定a、b的值;
(2)若b=1,求证:△OAC∽△OCB.
【分析】(1)根据OC=2可以得到C(0,2);然后通过解直角△OBC求得线段OB=2,则B(0,2),将其代入函数解析式求得a的值即可;
(2)欲证明△OAC∽△OCB,只需推知=即可.
【解答】(1)解:∵OC=2,∠OBC=30°,
∴OB===2.
∴B(2,0),C(0,2),
∴.
解得;
(2)证明:当b=1时,该抛物线解析式是y=x2﹣ax+1.
当x=0时,y=1,即C(0,1),此时OC=1.
设点A、B的横坐标分别是x1、x2,
令y=0,则x2﹣ax+1=0.
由根与系数的关系得到:x1 x2=1,即OA OB=1,
∴OA=.
∴=.
∵OC=1,
∴=.
又∵∠COA=∠BOC,
∴△OAC∽△OCB.
八、(本大题共1小题,每小题14分,总计14分)
23.已知:如图1,点D为等边△ABC边AB上一点,点E为边AC上一点.
(1)若点D为AB中点,∠CDE=60°.
①求∠AED的度数;
②如图2,连接BE,以点B为角的顶点,BE为一边作∠EBG=60°,交线段DC的延长线于点G.若AB=4,求线段CG的长.
(2)如图3,若AD:DB=2:1,点F为BC的中点,且∠EDF=60°,求的值.
【分析】(1)①根据△ABC是等边三角形三线合一的性质可得∠ACD=ACB=30°,进而可以解决问题;
②根据等边三角形的性质可得∠ADE=30°,然后根据含30度角的直角三角形求出DE的长,证明△BDE∽△BCG,对应边成比例即可解决问题;
(2)证明△AED∽△BDF,可得=,根据AD:DB=2:1,可得BD=AB,AD=AB,根据点F为BC的中点,可得BF=BC=AB,进而可以解决问题.
解:(1)①∵△ABC是等边三角形,点D为AB中点,
∴∠ACD=ACB=30°,
∵∠CDE=60°.
∴∠AED=∠ACD+∠CDE=90°;
②∵△ABC是等边三角形,
∴AB=AC=4,∠A=∠ABC=∠ACB=60°,
∵点D为AB中点,
∴∠CDB=90°,AD=DB=AB=2,∠DCB=ACB=30°,
∵∠AED=90°,
∴∠ADE=30°,
∴AE=AD=1,
∴DE==,
∵∠EBG=∠EBC+∠CBG=60°,∠ABC=∠EBC+∠ABE=60°,
∴∠ABE=∠CBG,
∵∠BDE=∠CDE+∠CDB=60°+90°=150°,
∠BCG=180°﹣∠BCD=180°﹣30°=150°,
∴∠BDE=∠BCG,
∴△BDE∽△BCG,
∴=,
∴=,
∴CG=2;
(2)∵∠EDF=60°,
∴∠ADE+∠BDF=180°﹣∠EDF=120°,
∠ADE+∠AED=180°﹣∠A=120°,
∴∠AED=∠BDF,
∵∠A=∠B=60°,
∴△AED∽△BDF,
∴=,
∵AD:DB=2:1,
∴BD=AB,AD=AB,
∵点F为BC的中点,
∴BF=BC=AB,
∴=,
∴=,
∴=,
∴=.
同课章节目录
