期中考试复习:统计与概率
图片预览

文档简介
期中考试复习六:统计与概率20121029 姓名: 学号:
1.(东城二模文)某校为了解学生的学科学习兴趣,对初高中学生做了一个喜欢数学和喜欢语文的抽样调查,随机抽取了名学生,相关的数据如下表所示:
数学
语文
总计
初中
高中
总计
(Ⅰ) 用分层抽样的方法从喜欢语文的学生中随机抽取名,高中学生应该抽取几名?
(Ⅱ) 在(Ⅰ)中抽取的名学生中任取名,求恰有名初中学生的概率.
2.(朝阳二模)高三年级进行模拟考试,某班参加考试的40名同学的成绩统计如下:
分数段
(70,90)
[90,100)
[100,120)
[120,150]
人数
5
a
15
b
规定分数在90分及以上为及格,120分及以上为优秀,成绩高于85分低于90分的同学为希望生.已知该班希望生有2名.
(Ⅰ)从该班所有学生中任选一名,求其成绩及格的概率;
(Ⅱ)当a =11时,从该班所有学生中任选一名,求其成绩优秀的概率;
(Ⅲ)从分数在(70,90)的5名学生中,任选2名同学参加辅导,求其中恰有1名希望生
的概率.
3.(丰台二模)某地区农科所为了选择更适应本地区种植的棉花品种,在该地区选择了5块土地,每块土地平均分成面积相等的两部分,分别种植甲、乙两个品种的棉花,收获时测得棉花的亩产量如下图所示:
(Ⅰ)请问甲、乙两种棉花哪种亩产量更稳定,并说明理由;
(Ⅱ)求从种植甲种棉花的5块土地中任选2块土地,这两块土地的亩产量均超过种植甲种棉花的5块土地的总平均亩产量的概率.
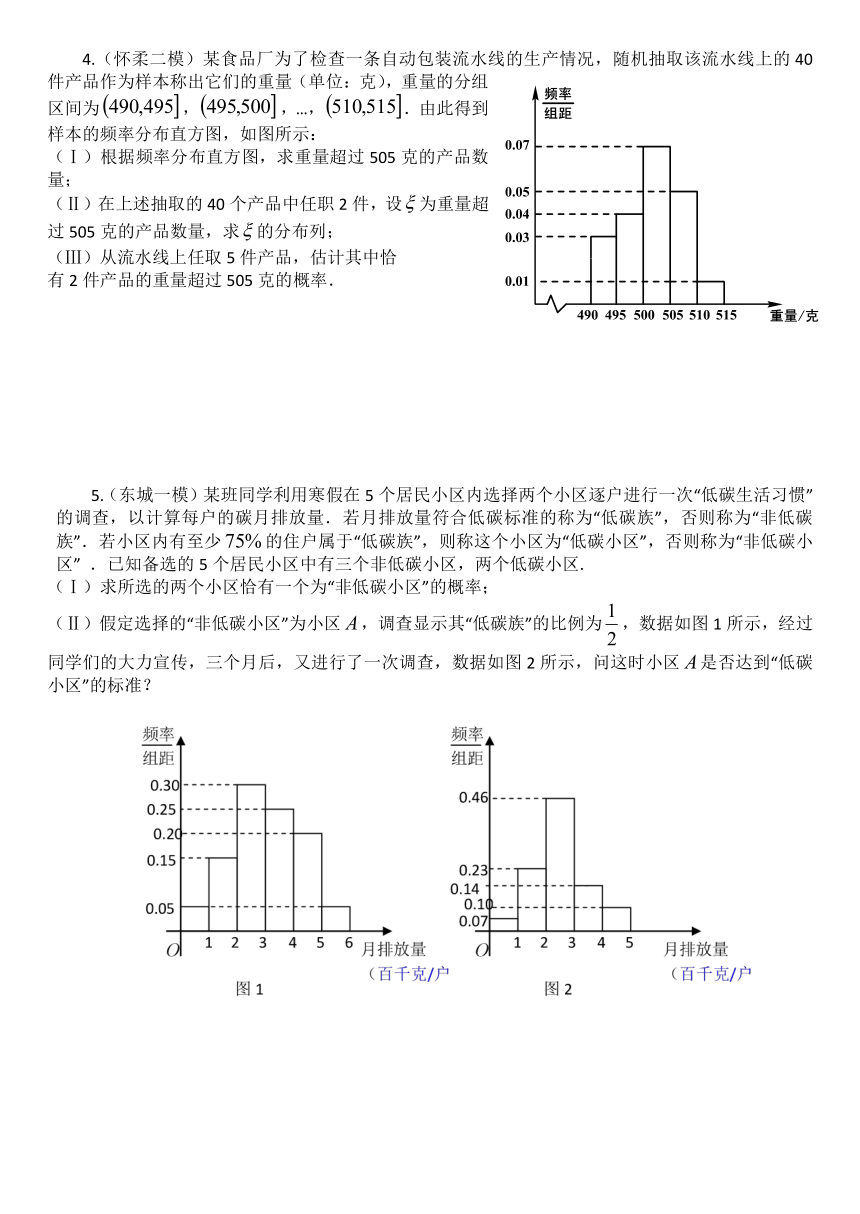
4.(怀柔二模)某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的40件产品作为样本称出它们的重量(单位:克),重量的分组区间为/,/,…,/.由此得到样本的频率分布直方图,如图所示:
(Ⅰ)根据频率分布直方图,求重量超过505克的产品数量;
(Ⅱ)在上述抽取的40个产品中任职2件,设/为重量超过505克的产品数量,求/的分布列;
(Ⅲ)从流水线上任取5件产品,估计其中恰
有2件产品的重量超过505克的概率.
5.(东城一模)某班同学利用寒假在5个居民小区内选择两个小区逐户进行一次“低碳生活习惯”的调查,以计算每户的碳月排放量.若月排放量符合低碳标准的称为“低碳族”,否则称为“非低碳族”.若小区内有至少的住户属于“低碳族”,则称这个小区为“低碳小区”,否则称为“非低碳小区” .已知备选的5个居民小区中有三个非低碳小区,两个低碳小区.
(Ⅰ)求所选的两个小区恰有一个为“非低碳小区”的概率;
(Ⅱ)假定选择的“非低碳小区”为小区,调查显示其“低碳族”的比例为,数据如图1所示,经过同学们的大力宣传,三个月后,又进行了一次调查,数据如图2所示,问这时小区是否达到“低碳小区”的标准?
6(石景山一模)我区高三期末统一测试中某校的数学成绩分组统计如下表:
(Ⅰ)求出表中、、、的值,并根据表中所给数据在下面给出的 坐标系中画出频率分布直方图;
分组
频数
频率
合计
(Ⅱ)若我区参加本次考试的学生有600人,试估计这次测试中我区成绩在分以上的人数;
(Ⅲ)若该校教师拟从分数不超过60的学生中选取2人进行个案分析,求被选中2人分数不超过30分的概率.
7.(密云一模)某高校在2011年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示.
(Ⅰ)分别求第3,4,5组的频率;
(Ⅱ)若该校决定在笔试成绩高的第3,4,5组中用分层抽样的方法抽取6名学生进入第二轮面试,求第3,4,5组每组各抽取多少名学生进入第二轮面试?
(Ⅲ)在(Ⅱ)的前提下,学校决定在这6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有一名学生被甲考官面试的概率.
8.(门头沟一模)甲、乙两名考生在填报志愿的时候都选中了A、B、C、D四所需要面试的院校,但是它们的面试安排在同一时间了。因此甲、乙只能在这四所院校中选择一个做志愿,假设每个院校被选择的机率相等,试求:
(I)甲乙选择同一所院校的概率;
(II)院校A、B至少有一所被选择的概率;
(III)院校A没有被选择的概率.
9.(海淀一模)某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是,样本数据分组为,,,,.
(Ⅰ)求直方图中的值;
(Ⅱ)如果上学所需时间不少于1小时的学生可申请在学校住宿,请估计学校600名新生中有多少名学生可以申请住宿.
10.(朝阳一模)某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如右图所示.
(Ⅰ)下表是年龄的频数分布表,求正整数的值;
区间
[25,30)
[30,35)
[35,40)
[40,45)
[45,50]
人数
50
50
150
(Ⅱ)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,年龄在第1,2,3组的人数分别是多少?
(Ⅲ)在(Ⅱ)的前提下,从这6人中随机抽取2人参加社区宣传交流活动,求至少有1人年龄在第3组的概率.
1.(东城二模文)某校为了解学生的学科学习兴趣,对初高中学生做了一个喜欢数学和喜欢语文的抽样调查,随机抽取了名学生,相关的数据如下表所示:
数学
语文
总计
初中
高中
总计
(Ⅰ) 用分层抽样的方法从喜欢语文的学生中随机抽取名,高中学生应该抽取几名?
(Ⅱ) 在(Ⅰ)中抽取的名学生中任取名,求恰有名初中学生的概率.
2.(朝阳二模)高三年级进行模拟考试,某班参加考试的40名同学的成绩统计如下:
分数段
(70,90)
[90,100)
[100,120)
[120,150]
人数
5
a
15
b
规定分数在90分及以上为及格,120分及以上为优秀,成绩高于85分低于90分的同学为希望生.已知该班希望生有2名.
(Ⅰ)从该班所有学生中任选一名,求其成绩及格的概率;
(Ⅱ)当a =11时,从该班所有学生中任选一名,求其成绩优秀的概率;
(Ⅲ)从分数在(70,90)的5名学生中,任选2名同学参加辅导,求其中恰有1名希望生
的概率.
3.(丰台二模)某地区农科所为了选择更适应本地区种植的棉花品种,在该地区选择了5块土地,每块土地平均分成面积相等的两部分,分别种植甲、乙两个品种的棉花,收获时测得棉花的亩产量如下图所示:
(Ⅰ)请问甲、乙两种棉花哪种亩产量更稳定,并说明理由;
(Ⅱ)求从种植甲种棉花的5块土地中任选2块土地,这两块土地的亩产量均超过种植甲种棉花的5块土地的总平均亩产量的概率.
4.(怀柔二模)某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的40件产品作为样本称出它们的重量(单位:克),重量的分组区间为/,/,…,/.由此得到样本的频率分布直方图,如图所示:
(Ⅰ)根据频率分布直方图,求重量超过505克的产品数量;
(Ⅱ)在上述抽取的40个产品中任职2件,设/为重量超过505克的产品数量,求/的分布列;
(Ⅲ)从流水线上任取5件产品,估计其中恰
有2件产品的重量超过505克的概率.
5.(东城一模)某班同学利用寒假在5个居民小区内选择两个小区逐户进行一次“低碳生活习惯”的调查,以计算每户的碳月排放量.若月排放量符合低碳标准的称为“低碳族”,否则称为“非低碳族”.若小区内有至少的住户属于“低碳族”,则称这个小区为“低碳小区”,否则称为“非低碳小区” .已知备选的5个居民小区中有三个非低碳小区,两个低碳小区.
(Ⅰ)求所选的两个小区恰有一个为“非低碳小区”的概率;
(Ⅱ)假定选择的“非低碳小区”为小区,调查显示其“低碳族”的比例为,数据如图1所示,经过同学们的大力宣传,三个月后,又进行了一次调查,数据如图2所示,问这时小区是否达到“低碳小区”的标准?
6(石景山一模)我区高三期末统一测试中某校的数学成绩分组统计如下表:
(Ⅰ)求出表中、、、的值,并根据表中所给数据在下面给出的 坐标系中画出频率分布直方图;
分组
频数
频率
合计
(Ⅱ)若我区参加本次考试的学生有600人,试估计这次测试中我区成绩在分以上的人数;
(Ⅲ)若该校教师拟从分数不超过60的学生中选取2人进行个案分析,求被选中2人分数不超过30分的概率.
7.(密云一模)某高校在2011年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示.
(Ⅰ)分别求第3,4,5组的频率;
(Ⅱ)若该校决定在笔试成绩高的第3,4,5组中用分层抽样的方法抽取6名学生进入第二轮面试,求第3,4,5组每组各抽取多少名学生进入第二轮面试?
(Ⅲ)在(Ⅱ)的前提下,学校决定在这6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有一名学生被甲考官面试的概率.
8.(门头沟一模)甲、乙两名考生在填报志愿的时候都选中了A、B、C、D四所需要面试的院校,但是它们的面试安排在同一时间了。因此甲、乙只能在这四所院校中选择一个做志愿,假设每个院校被选择的机率相等,试求:
(I)甲乙选择同一所院校的概率;
(II)院校A、B至少有一所被选择的概率;
(III)院校A没有被选择的概率.
9.(海淀一模)某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是,样本数据分组为,,,,.
(Ⅰ)求直方图中的值;
(Ⅱ)如果上学所需时间不少于1小时的学生可申请在学校住宿,请估计学校600名新生中有多少名学生可以申请住宿.
10.(朝阳一模)某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如右图所示.
(Ⅰ)下表是年龄的频数分布表,求正整数的值;
区间
[25,30)
[30,35)
[35,40)
[40,45)
[45,50]
人数
50
50
150
(Ⅱ)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,年龄在第1,2,3组的人数分别是多少?
(Ⅲ)在(Ⅱ)的前提下,从这6人中随机抽取2人参加社区宣传交流活动,求至少有1人年龄在第3组的概率.
