4.8.1图形的位似(1)(共26张PPT)
文档属性
| 名称 | 4.8.1图形的位似(1)(共26张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 939.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-04 00:00:00 | ||
图片预览




文档简介
(共26张PPT)
4.8.1图形的位似1
第四章
图形的相似
2021-2022学年九年级数学上册同步(北师版)
学习目标
1.理解位似多边形的定义及相关性质.
2.理解相似多边形与位似多边形的联系与区别.
3.初步了解利用图形的位似将一个图形放大或缩小做理论依据.
导入新课
1. 前面我们已经学习了图形的哪些变换?
相似:相似比.
平移:平移的方向,平移的距离.
注:图形这些不同的变换是我们学习几何必不可少的重要工具,它不但装点了我们的生活,而且是学习后续知识的基础.
下面请欣赏如下图形的变换
旋转:(中心对称)旋转中心,旋转方向,旋转角度.
轴对称:对称轴,
导入新课
如图,是幻灯机放映图片的示意图,在幻灯机放映图片的过程中,这些图片之间有什么关系?
连接图片上对应的点,你有什么发现?
位似多边形的概念
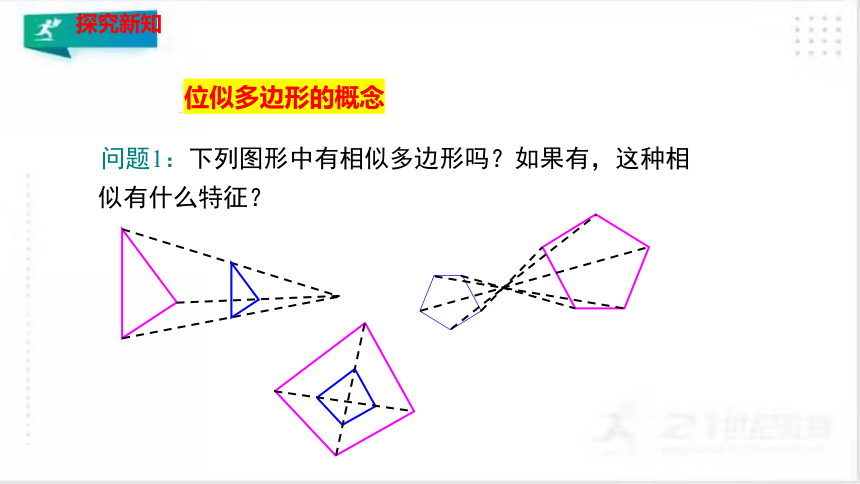
问题1:下列图形中有相似多边形吗?如果有,这种相似有什么特征?
探究新知
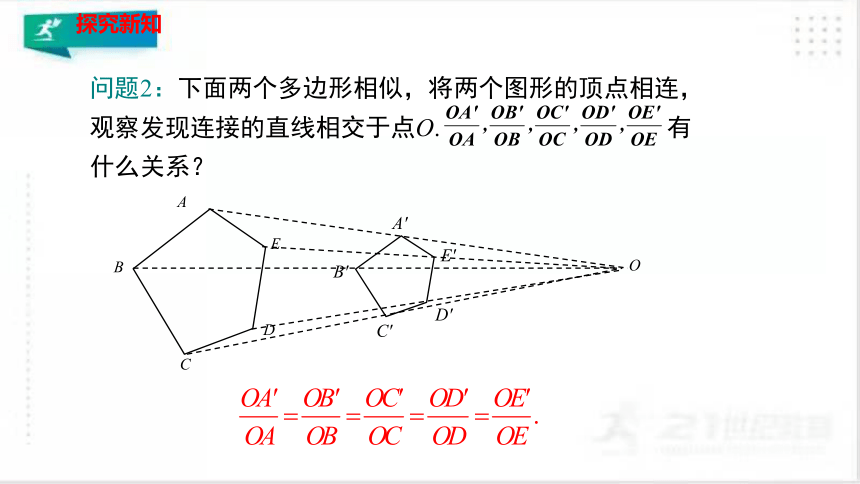
问题2:下面两个多边形相似,将两个图形的顶点相连,观察发现连接的直线相交于点O. 有什么关系?
A
B
C
D
E
E'
D'
C'
B'
A'
O
探究新知
总结
如果两个相似多边形任意一组对应顶点P,P 所在的直线都过同一点O,且OP =k· OP (k≠0),那么这样的两个多边形叫做位似多边形,点O叫做位似中心.其中k为相似多边形的相似比.
探究新知
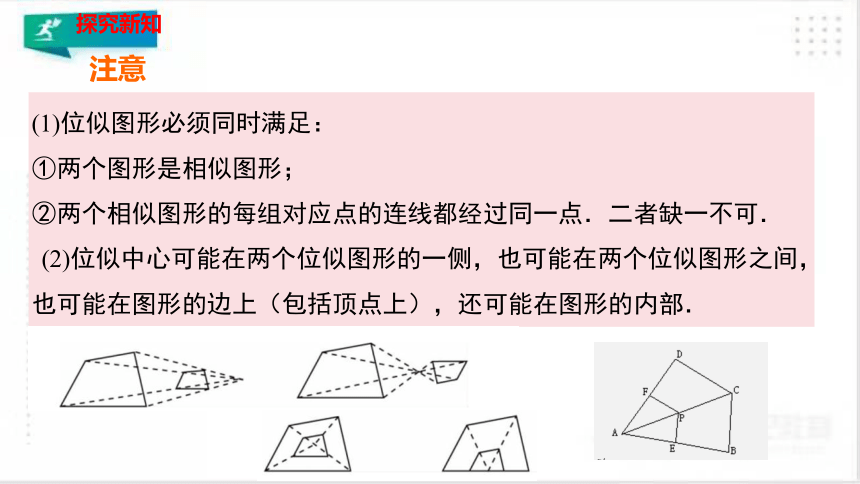
注意
(1)位似图形必须同时满足:
①两个图形是相似图形;
②两个相似图形的每组对应点的连线都经过同一点.二者缺一不可.
(2)位似中心可能在两个位似图形的一侧,也可能在两个位似图形之间,也可能在图形的边上(包括顶点上),还可能在图形的内部.
探究新知
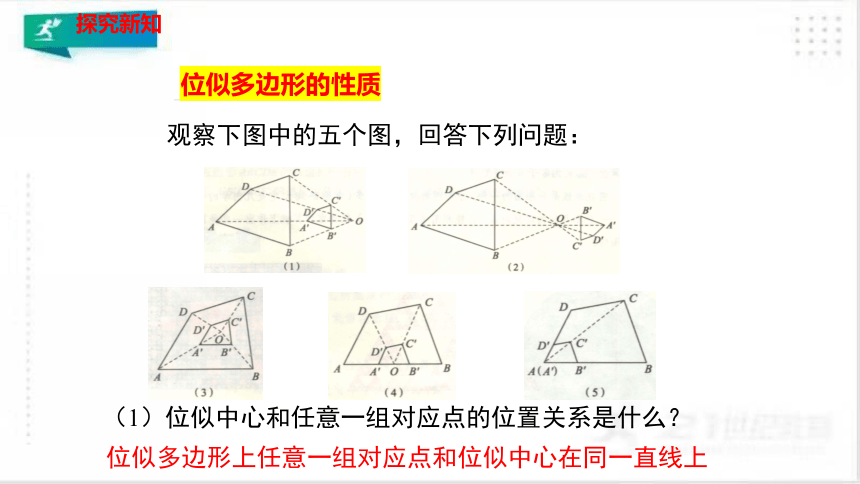
位似多边形的性质
观察下图中的五个图,回答下列问题:
(1)位似中心和任意一组对应点的位置关系是什么?
位似多边形上任意一组对应点和位似中心在同一直线上
探究新知
观察下图中的五个图,回答下列问题:
(2)任意一组对应线段的位置关系是什么?
位似多边形中的对应线段平行(或在一条直线上).
探究新知
观察下图中的五个图,回答下列问题:
(3)任意一组对应点到位似中心的距离比K与相似比有什么关系?
任意一组对应点到位似中心的距离之比k等于相似比.
探究新知
位似图形的性质
(2)位似图形上任意一对对应点到位似中心的距离之比等于相似比.
小结
(4)位似图形中的对应线段平行(或在一条直线上).
(1)位似图形是相似图形,具备相似图形的所有性质
(3) 位似图形上对应点和位似中心在同一直线上。
探究新知
位似多边形的画法
例 如图,已知△ABC,以点O为位似中心画△DEF,使它与△ABC位似,且相似比为2.
解:如图,画射线OA,OB,OC
在射线OA,OB,OC上分别取点
D,E,F,使OD=2OA
OE=2OB,OF=2OC
顺次连接D,E,F,
则△ DEF与△ABC位似
相似比为2
A
B
F
E
D
O
满足条件△DEF可以在点O的另一侧吗?
探究新知
画法二:△ABC与△DEF异侧
解:画射线OA,OB,OC;
沿着射线OA,OB,OC反方向上分别
取点D,E,F,
OD = 2OA,OE = 2OB,OF = 2OC;
顺序连接D,E,F,使△DEF与
△ABC 位似,相似比为2.
B
C
O
E
F
D
A
探究新知
①确定位似中心,位似中心的位置可随意选择;
②确定原图形的关键点,如四边形有四个关键点,即它的四个顶点;
③确定位似比,根据位似比的取值,可以判断是将一个图形放大还是缩小,并连接对应点;
④符合要求的图形不唯一,因为所作的图形与所确定的位似中心的位置有关,并且同一个位似中心的两侧各有一个符合要求的图形。
位似变换的步骤
探究新知
1.下列关于位似图形的三个表述中正确的有( )
①相似图形一定是位似图形,位似图形一定是相似图形;
②位似图形一定有位似中心;
③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么这两个图形是位似图形.
A.0个 B.1个 C.2个 D.3个
C
课堂练习
2.下列各选项的两个图形中,不是位似图形的是( )
C
课堂练习
3. 如图,△ABC与△DEF是位似图形,位似比为2 : 3,已知 AB=4,则 DE 的长为___.
6
课堂练习
是位似图形
位似中心是点A
位似比是1:2
4.如图P,E,F分别是AC,AB,AD的中点,四边形AEPF与四边形ABCD是位似图形吗?如果是位似图形,说出位似中心和位似比.
课堂练习
5.把四边形 ABCD 缩小到原来的 1/2.
(3) 顺次连接点 A' 、B' 、C' 、D' ,所得四边形 A' B' C' D' 就是所要求的图形.
(1) 在四边形外任选一点 O (如图);
(2) 分别在线段 OA、OB、OC、OD (或延长线)上取点 A' 、B' 、C' 、D' ,使得 ;
课堂练习
O
D
A
B
C
A'
B'
C'
D'
O
D
A
B
C
A'
B'
C'
D'
课堂练习
思维拓展
如图,△ABC. 根据要求作△A'B'C',使△A' B' C'∽△ABC,且相似比为 1 : 5.
(1) 位似中心在△ABC的一条边AB上;
假设位似中心点 O 为 AB中点,点 O 位置如图所示.
根据相似比可确定 A′,
B′,C′ 的位置.
A
C
B
O
●
A′
B′
C′
●
●
●
(2) 以点 C 为位似中心.
C
A
B
A′
B′
( C′ )
●
●
●
课堂小结
位似多边形
及其性质
定义
性质
如果两个相似多边形任意一组对应顶点P,
P 所在的直线都过同一点O,且OP =k· OP
(k≠0),那么这样的两个多边形叫做位似多边形.
作位似图形:关键是确定位似中心、
相似比和找关键点的对应点.
① 两个图形相似.
②对应点的连线相较于一点,对应边互相
平行或在同一直线上.
③任意一对对应点到位似中心的距离之比
等于相似比.
画法
https://www.21cnjy.com/help/help_extract.php
4.8.1图形的位似1
第四章
图形的相似
2021-2022学年九年级数学上册同步(北师版)
学习目标
1.理解位似多边形的定义及相关性质.
2.理解相似多边形与位似多边形的联系与区别.
3.初步了解利用图形的位似将一个图形放大或缩小做理论依据.
导入新课
1. 前面我们已经学习了图形的哪些变换?
相似:相似比.
平移:平移的方向,平移的距离.
注:图形这些不同的变换是我们学习几何必不可少的重要工具,它不但装点了我们的生活,而且是学习后续知识的基础.
下面请欣赏如下图形的变换
旋转:(中心对称)旋转中心,旋转方向,旋转角度.
轴对称:对称轴,
导入新课
如图,是幻灯机放映图片的示意图,在幻灯机放映图片的过程中,这些图片之间有什么关系?
连接图片上对应的点,你有什么发现?
位似多边形的概念
问题1:下列图形中有相似多边形吗?如果有,这种相似有什么特征?
探究新知
问题2:下面两个多边形相似,将两个图形的顶点相连,观察发现连接的直线相交于点O. 有什么关系?
A
B
C
D
E
E'
D'
C'
B'
A'
O
探究新知
总结
如果两个相似多边形任意一组对应顶点P,P 所在的直线都过同一点O,且OP =k· OP (k≠0),那么这样的两个多边形叫做位似多边形,点O叫做位似中心.其中k为相似多边形的相似比.
探究新知
注意
(1)位似图形必须同时满足:
①两个图形是相似图形;
②两个相似图形的每组对应点的连线都经过同一点.二者缺一不可.
(2)位似中心可能在两个位似图形的一侧,也可能在两个位似图形之间,也可能在图形的边上(包括顶点上),还可能在图形的内部.
探究新知
位似多边形的性质
观察下图中的五个图,回答下列问题:
(1)位似中心和任意一组对应点的位置关系是什么?
位似多边形上任意一组对应点和位似中心在同一直线上
探究新知
观察下图中的五个图,回答下列问题:
(2)任意一组对应线段的位置关系是什么?
位似多边形中的对应线段平行(或在一条直线上).
探究新知
观察下图中的五个图,回答下列问题:
(3)任意一组对应点到位似中心的距离比K与相似比有什么关系?
任意一组对应点到位似中心的距离之比k等于相似比.
探究新知
位似图形的性质
(2)位似图形上任意一对对应点到位似中心的距离之比等于相似比.
小结
(4)位似图形中的对应线段平行(或在一条直线上).
(1)位似图形是相似图形,具备相似图形的所有性质
(3) 位似图形上对应点和位似中心在同一直线上。
探究新知
位似多边形的画法
例 如图,已知△ABC,以点O为位似中心画△DEF,使它与△ABC位似,且相似比为2.
解:如图,画射线OA,OB,OC
在射线OA,OB,OC上分别取点
D,E,F,使OD=2OA
OE=2OB,OF=2OC
顺次连接D,E,F,
则△ DEF与△ABC位似
相似比为2
A
B
F
E
D
O
满足条件△DEF可以在点O的另一侧吗?
探究新知
画法二:△ABC与△DEF异侧
解:画射线OA,OB,OC;
沿着射线OA,OB,OC反方向上分别
取点D,E,F,
OD = 2OA,OE = 2OB,OF = 2OC;
顺序连接D,E,F,使△DEF与
△ABC 位似,相似比为2.
B
C
O
E
F
D
A
探究新知
①确定位似中心,位似中心的位置可随意选择;
②确定原图形的关键点,如四边形有四个关键点,即它的四个顶点;
③确定位似比,根据位似比的取值,可以判断是将一个图形放大还是缩小,并连接对应点;
④符合要求的图形不唯一,因为所作的图形与所确定的位似中心的位置有关,并且同一个位似中心的两侧各有一个符合要求的图形。
位似变换的步骤
探究新知
1.下列关于位似图形的三个表述中正确的有( )
①相似图形一定是位似图形,位似图形一定是相似图形;
②位似图形一定有位似中心;
③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么这两个图形是位似图形.
A.0个 B.1个 C.2个 D.3个
C
课堂练习
2.下列各选项的两个图形中,不是位似图形的是( )
C
课堂练习
3. 如图,△ABC与△DEF是位似图形,位似比为2 : 3,已知 AB=4,则 DE 的长为___.
6
课堂练习
是位似图形
位似中心是点A
位似比是1:2
4.如图P,E,F分别是AC,AB,AD的中点,四边形AEPF与四边形ABCD是位似图形吗?如果是位似图形,说出位似中心和位似比.
课堂练习
5.把四边形 ABCD 缩小到原来的 1/2.
(3) 顺次连接点 A' 、B' 、C' 、D' ,所得四边形 A' B' C' D' 就是所要求的图形.
(1) 在四边形外任选一点 O (如图);
(2) 分别在线段 OA、OB、OC、OD (或延长线)上取点 A' 、B' 、C' 、D' ,使得 ;
课堂练习
O
D
A
B
C
A'
B'
C'
D'
O
D
A
B
C
A'
B'
C'
D'
课堂练习
思维拓展
如图,△ABC. 根据要求作△A'B'C',使△A' B' C'∽△ABC,且相似比为 1 : 5.
(1) 位似中心在△ABC的一条边AB上;
假设位似中心点 O 为 AB中点,点 O 位置如图所示.
根据相似比可确定 A′,
B′,C′ 的位置.
A
C
B
O
●
A′
B′
C′
●
●
●
(2) 以点 C 为位似中心.
C
A
B
A′
B′
( C′ )
●
●
●
课堂小结
位似多边形
及其性质
定义
性质
如果两个相似多边形任意一组对应顶点P,
P 所在的直线都过同一点O,且OP =k· OP
(k≠0),那么这样的两个多边形叫做位似多边形.
作位似图形:关键是确定位似中心、
相似比和找关键点的对应点.
① 两个图形相似.
②对应点的连线相较于一点,对应边互相
平行或在同一直线上.
③任意一对对应点到位似中心的距离之比
等于相似比.
画法
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
