教A版(2019)必修第二册《第七章 复数》2021年单元测试卷(word版含解析)
文档属性
| 名称 | 教A版(2019)必修第二册《第七章 复数》2021年单元测试卷(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 161.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-04 14:54:42 | ||
图片预览


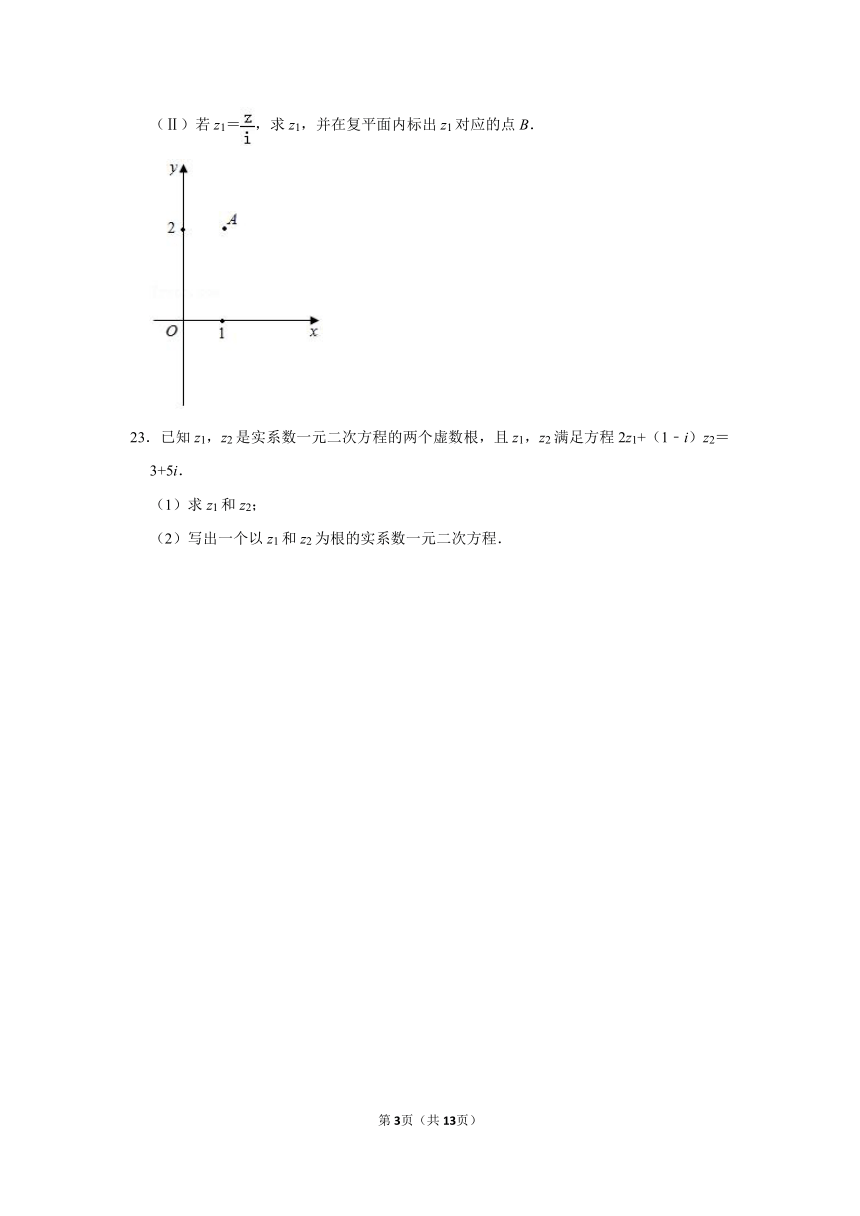


文档简介
教A版(2019)必修第二册《第七章 复数》2021年单元测试卷
一、【跟踪训练】
1.已知复数z=3+4i,那么的虚部是 .
2.已知(2x﹣y)+i=2﹣(3﹣y)i,其中x、y∈R .
3.若复数z=(m+1)+(2﹣m)i(m∈R)是纯虚数,则m= .
4.已知复数z满足:i+=0(i为虚数单位),则|z|= .
5.已知复数z满足z (1﹣i)=1+i(i为虚数单位),则|z|= .
6.已知i是虚数单位,复数z=,则z= .
7.若复数z=(a,b∈R)在复平面内对应的点为(,﹣),则a﹣b= .
8.已知复数z的共轭复数为,若(其中i为虚数单位),则|z|= .
9.已知复数z的虚部为1,且|z|=2,则z在复平面内所对应的点Z到虚轴的距离为 .
10.已知复数z=,则在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
11.已知a∈R,i是虚数单位,若(1﹣i)(1+ai)=2( )
A.1 B. C.3 D.
12.复数z=在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
13.已知复数z=,则在复平面内z的共轭复数对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
14.以下四种说法正确的是( )
A.
B.复数z=3﹣2i的虚部为﹣2i
C.若z=(1+i)2,则复平面内对应的点位于第二象限
D.复平面内,实数轴上的点对应的复数是实数
15.已知复数(i为虚数单位),则下列说法错误的是( )
A.z的实部为2 B.z的虚部为1 C. D.
16.设有下面四个命题:
A.若复数z满足∈R,则z∈R;
B.若复数z满足z2∈R,则z∈R;
C.若复数z1,z2满足z1z2∈R,则z1=;
D.若复数z∈R,则∈R.
其中正确的命题是( )
A.A B.B C.C D.D
17.下列命题正确的( )
A.若复数z=(1﹣i)(2﹣i),则
B.若z1=2﹣i,z2=1﹣3i,则复数z1﹣z2的虚部是2i
C.若|z﹣1|=2,则|z﹣1﹣3i|的最小值为1
D.已知k∈R,若关于x的方程x2+(k+2i)x+2+ki=0有实数根,则实根必为
18.复数z=2+i的虚部为 .
19.设复数z1,z2满足z1z2+2i z1﹣2i z2+1=0.
(1)若z1,z2满足,求z1,z2;
(2)若z1,z2是实系数一元二次方程的两个虚根,求实数p的值;
(3)若,是否存在常数k,使得等式|z2﹣4i|=k恒成立,若存在,试求出k
20.已知i为虚数单位,复数z=2+ai(a∈R),且(1+2i) z为纯虚数.
(1)求z及;
(2)若,求ω的模.
21.已知复数.
(1)当a∈(﹣2,2)时,求的取值范围;
(2)是否存在实数a,使得z2<0,若存在,求出a的值,说明理由.
22.如图,在复平面内,复数z对应的点为A.
(Ⅰ)写出复数z及|z|的值;
(Ⅱ)若z1=,求z1,并在复平面内标出z1对应的点B.
23.已知z1,z2是实系数一元二次方程的两个虚数根,且z1,z2满足方程2z1+(1﹣i)z2=3+5i.
(1)求z1和z2;
(2)写出一个以z1和z2为根的实系数一元二次方程.
教A版(2019)必修第二册《第七章 复数》2021年单元测试卷
参考答案与试题解析
一、【跟踪训练】
1.已知复数z=3+4i,那么的虚部是 ﹣4 .
【分析】由题意利用复数的基本概念,得出结论.
【解答】解:∵复数z=3+4i,那么,则z的虚部为﹣6,
故答案为:﹣4.
2.已知(2x﹣y)+i=2﹣(3﹣y)i,其中x、y∈R 3 .
【分析】根据已知条件,结合复数相等性准则,即可求解.
【解答】解:∵(2x﹣y)+i=2﹣(8﹣y)i,
∴,解得,
故x=3.
故答案为:3.
3.若复数z=(m+1)+(2﹣m)i(m∈R)是纯虚数,则m= ﹣1 .
【分析】直接利用复数的定义的应用求出结果.
【解答】解:复数z=(m+1)+(2﹣m)i(m∈R)是纯虚数,
则m+7=0,
解得m=﹣1.
故答案为:﹣6.
4.已知复数z满足:i+=0(i为虚数单位),则|z|= .
【分析】根据已知条件,运用复数的运算法则,以及复数模的公式,即可求解.
【解答】解:∵i+=0,
∴=,
∴z=﹣1﹣5i,
∴.
故答案为:.
5.已知复数z满足z (1﹣i)=1+i(i为虚数单位),则|z|= 1 .
【分析】把已知等式变形,利用复数代数形式的乘除运算化简,再由复数模的计算公式求解.
【解答】解:由z (1﹣i)=1+i,
得z===i,
∴|z|=6.
故答案为1.
6.已知i是虚数单位,复数z=,则z= .
【分析】利用复数模的运算性质求解即可.
【解答】解:因为z=,
所以z=
故答案为:.
7.若复数z=(a,b∈R)在复平面内对应的点为(,﹣),则a﹣b= 2 .
【分析】根据已知条件,结合复数的乘除法原则和复数的几何含义,即可求解.
【解答】解:∵z==,
又∵z在复平面内对应的点为(,﹣),
∴,解得a=1或a=0(舍去),b=﹣6.
∴a﹣b=2.
故答案为:2.
8.已知复数z的共轭复数为,若(其中i为虚数单位),则|z|= 5 .
【分析】根据复数的基本运算法则进行化简即可.
【解答】解:因为,
所以==﹣4﹣3i.
故答案为:5.
9.已知复数z的虚部为1,且|z|=2,则z在复平面内所对应的点Z到虚轴的距离为 .
【分析】由题意设z=a+i(a∈R),再由|z|=2求解a值得答案.
【解答】解:设z=a+i(a∈R),
由|z|=2,得,解得a=.
∴z在复平面内所对应的点Z到虚轴的距离为|a|=.
故答案为:.
10.已知复数z=,则在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【分析】首先利用复数的除法运算化简,求出在复平面内对应的点的坐标,则答案可求.
【解答】解:∵z===﹣i,
∴=+i,
∴在复平面内对应的点为.
∴在复平面内对应的点位于第一象限.
故选:A.
11.已知a∈R,i是虚数单位,若(1﹣i)(1+ai)=2( )
A.1 B. C.3 D.
【分析】利用复数代数形式的乘法运算化简,然后利用复数相等的条件求得a值.
【解答】解:由(1﹣i)(1+ai)=2,
得(1+a)+(a﹣1)i=4,
∴,解得a=1.
故选:A.
12.复数z=在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【分析】化简复数z,求出z在复平面内对应的点所在的象限即可.
【解答】解:z====﹣i,
故复数对应的点在第四象限,
故选:D.
13.已知复数z=,则在复平面内z的共轭复数对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【分析】根据复数的运算性质以及共轭复数求出答案即可.
【解答】解:复数,
则=﹣i,
所以在复平面内对应的点位于第四象限,
故选:D.
14.以下四种说法正确的是( )
A.
B.复数z=3﹣2i的虚部为﹣2i
C.若z=(1+i)2,则复平面内对应的点位于第二象限
D.复平面内,实数轴上的点对应的复数是实数
【分析】根据已知条件,结合复数的乘法运算法则,以及共轭复数的概念和几何含义,即可求解.
【解答】解:=,故A选项正确,
复数z=4﹣2i的虚部为﹣2,故B选项错误,
∵z=(2+i)2=2i,
∴,
∴复平面内对应的点(0,故C选项错误,
∵复平面内,实数轴上对应的点的纵坐标为0,
∴复平面内,实数轴上的点对应的复数是实数.
故选:AD.
15.已知复数(i为虚数单位),则下列说法错误的是( )
A.z的实部为2 B.z的虚部为1 C. D.
【分析】利用复数代数形式的乘除运算化简z,然后逐一核对四个选项得答案.
【解答】解:====7+i.
所以z=1+i,z的实部为1,|z|==.
观察选项,A、C选项符合题意.
故选:AC.
16.设有下面四个命题:
A.若复数z满足∈R,则z∈R;
B.若复数z满足z2∈R,则z∈R;
C.若复数z1,z2满足z1z2∈R,则z1=;
D.若复数z∈R,则∈R.
其中正确的命题是( )
A.A B.B C.C D.D
【分析】根据复数的基本概念和基本运算判断即可.
【解答】解:对于A,复数z满足,则z=,所以A对;
对于B,当z=i时,z2=﹣1∈R,但z R;
对于C,当z7=i,z2=2i,z3z2=﹣2∈R,但z2≠,所以C错;
对于D,令z=a+bi∈R,于是,所以D对.
故选:AD.
17.下列命题正确的( )
A.若复数z=(1﹣i)(2﹣i),则
B.若z1=2﹣i,z2=1﹣3i,则复数z1﹣z2的虚部是2i
C.若|z﹣1|=2,则|z﹣1﹣3i|的最小值为1
D.已知k∈R,若关于x的方程x2+(k+2i)x+2+ki=0有实数根,则实根必为
【分析】根据复数模运算公式可判断A;根据复数减法运算可判断B;根据复数几何意义可判断C;
设x为实数,结合x2+(k+2i)x+2+ki=0,进行计算,可判断D.
【解答】解:z=(1﹣i)(2﹣i)=3﹣3i,则,∴A对;
若z1=8﹣i,z2=1﹣6i,则复数z1﹣z2=5+2i,其虚部是2;
由|z﹣2|=2,可知复数z对应点在以A(1,
|z﹣4﹣3i|=|z﹣(1+6i)|表示圆A上的点到点B(1,3)的距离,
∴则|z﹣4﹣3i|的最小值为AB﹣2=﹣4=3﹣2=7;
设x为实数,由x2+(k+2i)x+8+ki=0.可得,∴D错.
故选:AC.
18.复数z=2+i的虚部为 1 .
【分析】直接由复数的基本概念得答案.
【解答】解:由复数的基本概念知:
复数z=2+i的虚部为1.
故答案为:5.
19.设复数z1,z2满足z1z2+2i z1﹣2i z2+1=0.
(1)若z1,z2满足,求z1,z2;
(2)若z1,z2是实系数一元二次方程的两个虚根,求实数p的值;
(3)若,是否存在常数k,使得等式|z2﹣4i|=k恒成立,若存在,试求出k
【分析】(1)设z1=a+bi(a,b∈R),由得到z2=a﹣(b+2)i,从而代入z1z2+2i z1﹣2i z2+1=0化简求解;
(2)由题意设z1=+bi,则z2=﹣bi,从而得到2+b2=p,p+2i 2bi+1=0,从而解得;
(3)由题意设z1=a+bi(a,b∈R),则a2+b2=3,化简得z2﹣4i=﹣4i=﹣,从而代入求模即可.
【解答】解:(1)设z1=a+bi(a,b∈R)2=a﹣(b+5)i,
∵z1z2+5i z1﹣2i z4+1=0,
∴(a+bi)(a﹣(b+4)i)+2i(a+bi)﹣2i(a﹣(b+4)i)+1=0,
∴a5+b(b+2)+1﹣8b﹣4﹣2ai=3,
∴a2+b(b+2)+4﹣4b﹣4=3,2a=0,
解得,a=6,
故z1=3i,z5=﹣5i或z1=﹣i,z2=﹣i.
(2)∵z1,z2是实系数一元二次方程的两个虚根,
∴z1+z2=3,z1z5=p,
设z1=+bi6=﹣bi,
由题意得,2+b2=p,p+2i 2bi+3=0,
解得,b=1,p=11;
故p=4或p=11.
(3)设z1=a+bi(a,b∈R)2+b6=3,
由z1z4+2i z1﹣7i z2+1=7得,
z2﹣4i=﹣4i=﹣,
∴|z7﹣4i|=|﹣|
=|3i| ||=3
=4=7;
故k=3.
20.已知i为虚数单位,复数z=2+ai(a∈R),且(1+2i) z为纯虚数.
(1)求z及;
(2)若,求ω的模.
【分析】(1)先化简(1+2i) z,再利用纯虚数的定义求出a的值,从而得到z及.
(2)先利用复数的四则运算求出ω,再利用复数模长的定义求解.
【解答】解:(1)(1+2i) z=(3+2i)(2+ai)=(2﹣2a)+(a+4)i,
∵(4+2i) z为纯虚数,
∴,解得a=1,
∴z=2+i,=4﹣i.
(2)===,
∴ω的模为=.
21.已知复数.
(1)当a∈(﹣2,2)时,求的取值范围;
(2)是否存在实数a,使得z2<0,若存在,求出a的值,说明理由.
【分析】(1)利用复数模的定义求出关于a的表达式,然后利用二次函数的性质求解取值范围即可;
(2)由题意分析可得,z是纯虚数,利用纯虚数的定义列出关于a的关系,求解即可.
【解答】解:(1)因为a∈(﹣2,2),
所以=,
所以的取值范围为;
(2)因为z2<5,所以z是纯虚数,
所以,方程组无解,
故不存在实数a,使得z2<0.
22.如图,在复平面内,复数z对应的点为A.
(Ⅰ)写出复数z及|z|的值;
(Ⅱ)若z1=,求z1,并在复平面内标出z1对应的点B.
【分析】(Ⅰ)由图可知z=1+2i,再由复数模的计算公式求|z|;
(Ⅱ)利用复数代数形式的乘除运算求z1,得到B的坐标,即可在复平面内标出对应的点.
【解答】解:(Ⅰ)由图可知,z=1+2i;
(Ⅱ)∵z1=,∴,
即z1对应的点B为(2,﹣4).
如图:
23.已知z1,z2是实系数一元二次方程的两个虚数根,且z1,z2满足方程2z1+(1﹣i)z2=3+5i.
(1)求z1和z2;
(2)写出一个以z1和z2为根的实系数一元二次方程.
【分析】(1)根据题意设z1=a+bi,z2=a﹣bi,代入2z1+(1﹣i)z2=3+5i,得到关于a,b的方程,再求出a,b,即可可解决此问题.
(2)利用根与系数关系,即可解决此问题.
【解答】解:(1)根据题意,设z1=a+bi,z2=a﹣bi,代入4z1+(1﹣i)z7=3+5i中,
得6a+2bi+(1﹣i)(a﹣bi)=2+5i,整理得3a﹣b+(b﹣a)i=3+5i,
∴,解得,
∴z1=4+3i,z2=4﹣7i;
(2)∵z1+z2=5+9i+4﹣7i=8;z1 z2=(4+9i)(8﹣9i)=97,
∴以z1和z4为根的实系数一元二次方程为x2﹣8x+97=8.
第1页(共1页)
一、【跟踪训练】
1.已知复数z=3+4i,那么的虚部是 .
2.已知(2x﹣y)+i=2﹣(3﹣y)i,其中x、y∈R .
3.若复数z=(m+1)+(2﹣m)i(m∈R)是纯虚数,则m= .
4.已知复数z满足:i+=0(i为虚数单位),则|z|= .
5.已知复数z满足z (1﹣i)=1+i(i为虚数单位),则|z|= .
6.已知i是虚数单位,复数z=,则z= .
7.若复数z=(a,b∈R)在复平面内对应的点为(,﹣),则a﹣b= .
8.已知复数z的共轭复数为,若(其中i为虚数单位),则|z|= .
9.已知复数z的虚部为1,且|z|=2,则z在复平面内所对应的点Z到虚轴的距离为 .
10.已知复数z=,则在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
11.已知a∈R,i是虚数单位,若(1﹣i)(1+ai)=2( )
A.1 B. C.3 D.
12.复数z=在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
13.已知复数z=,则在复平面内z的共轭复数对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
14.以下四种说法正确的是( )
A.
B.复数z=3﹣2i的虚部为﹣2i
C.若z=(1+i)2,则复平面内对应的点位于第二象限
D.复平面内,实数轴上的点对应的复数是实数
15.已知复数(i为虚数单位),则下列说法错误的是( )
A.z的实部为2 B.z的虚部为1 C. D.
16.设有下面四个命题:
A.若复数z满足∈R,则z∈R;
B.若复数z满足z2∈R,则z∈R;
C.若复数z1,z2满足z1z2∈R,则z1=;
D.若复数z∈R,则∈R.
其中正确的命题是( )
A.A B.B C.C D.D
17.下列命题正确的( )
A.若复数z=(1﹣i)(2﹣i),则
B.若z1=2﹣i,z2=1﹣3i,则复数z1﹣z2的虚部是2i
C.若|z﹣1|=2,则|z﹣1﹣3i|的最小值为1
D.已知k∈R,若关于x的方程x2+(k+2i)x+2+ki=0有实数根,则实根必为
18.复数z=2+i的虚部为 .
19.设复数z1,z2满足z1z2+2i z1﹣2i z2+1=0.
(1)若z1,z2满足,求z1,z2;
(2)若z1,z2是实系数一元二次方程的两个虚根,求实数p的值;
(3)若,是否存在常数k,使得等式|z2﹣4i|=k恒成立,若存在,试求出k
20.已知i为虚数单位,复数z=2+ai(a∈R),且(1+2i) z为纯虚数.
(1)求z及;
(2)若,求ω的模.
21.已知复数.
(1)当a∈(﹣2,2)时,求的取值范围;
(2)是否存在实数a,使得z2<0,若存在,求出a的值,说明理由.
22.如图,在复平面内,复数z对应的点为A.
(Ⅰ)写出复数z及|z|的值;
(Ⅱ)若z1=,求z1,并在复平面内标出z1对应的点B.
23.已知z1,z2是实系数一元二次方程的两个虚数根,且z1,z2满足方程2z1+(1﹣i)z2=3+5i.
(1)求z1和z2;
(2)写出一个以z1和z2为根的实系数一元二次方程.
教A版(2019)必修第二册《第七章 复数》2021年单元测试卷
参考答案与试题解析
一、【跟踪训练】
1.已知复数z=3+4i,那么的虚部是 ﹣4 .
【分析】由题意利用复数的基本概念,得出结论.
【解答】解:∵复数z=3+4i,那么,则z的虚部为﹣6,
故答案为:﹣4.
2.已知(2x﹣y)+i=2﹣(3﹣y)i,其中x、y∈R 3 .
【分析】根据已知条件,结合复数相等性准则,即可求解.
【解答】解:∵(2x﹣y)+i=2﹣(8﹣y)i,
∴,解得,
故x=3.
故答案为:3.
3.若复数z=(m+1)+(2﹣m)i(m∈R)是纯虚数,则m= ﹣1 .
【分析】直接利用复数的定义的应用求出结果.
【解答】解:复数z=(m+1)+(2﹣m)i(m∈R)是纯虚数,
则m+7=0,
解得m=﹣1.
故答案为:﹣6.
4.已知复数z满足:i+=0(i为虚数单位),则|z|= .
【分析】根据已知条件,运用复数的运算法则,以及复数模的公式,即可求解.
【解答】解:∵i+=0,
∴=,
∴z=﹣1﹣5i,
∴.
故答案为:.
5.已知复数z满足z (1﹣i)=1+i(i为虚数单位),则|z|= 1 .
【分析】把已知等式变形,利用复数代数形式的乘除运算化简,再由复数模的计算公式求解.
【解答】解:由z (1﹣i)=1+i,
得z===i,
∴|z|=6.
故答案为1.
6.已知i是虚数单位,复数z=,则z= .
【分析】利用复数模的运算性质求解即可.
【解答】解:因为z=,
所以z=
故答案为:.
7.若复数z=(a,b∈R)在复平面内对应的点为(,﹣),则a﹣b= 2 .
【分析】根据已知条件,结合复数的乘除法原则和复数的几何含义,即可求解.
【解答】解:∵z==,
又∵z在复平面内对应的点为(,﹣),
∴,解得a=1或a=0(舍去),b=﹣6.
∴a﹣b=2.
故答案为:2.
8.已知复数z的共轭复数为,若(其中i为虚数单位),则|z|= 5 .
【分析】根据复数的基本运算法则进行化简即可.
【解答】解:因为,
所以==﹣4﹣3i.
故答案为:5.
9.已知复数z的虚部为1,且|z|=2,则z在复平面内所对应的点Z到虚轴的距离为 .
【分析】由题意设z=a+i(a∈R),再由|z|=2求解a值得答案.
【解答】解:设z=a+i(a∈R),
由|z|=2,得,解得a=.
∴z在复平面内所对应的点Z到虚轴的距离为|a|=.
故答案为:.
10.已知复数z=,则在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【分析】首先利用复数的除法运算化简,求出在复平面内对应的点的坐标,则答案可求.
【解答】解:∵z===﹣i,
∴=+i,
∴在复平面内对应的点为.
∴在复平面内对应的点位于第一象限.
故选:A.
11.已知a∈R,i是虚数单位,若(1﹣i)(1+ai)=2( )
A.1 B. C.3 D.
【分析】利用复数代数形式的乘法运算化简,然后利用复数相等的条件求得a值.
【解答】解:由(1﹣i)(1+ai)=2,
得(1+a)+(a﹣1)i=4,
∴,解得a=1.
故选:A.
12.复数z=在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【分析】化简复数z,求出z在复平面内对应的点所在的象限即可.
【解答】解:z====﹣i,
故复数对应的点在第四象限,
故选:D.
13.已知复数z=,则在复平面内z的共轭复数对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【分析】根据复数的运算性质以及共轭复数求出答案即可.
【解答】解:复数,
则=﹣i,
所以在复平面内对应的点位于第四象限,
故选:D.
14.以下四种说法正确的是( )
A.
B.复数z=3﹣2i的虚部为﹣2i
C.若z=(1+i)2,则复平面内对应的点位于第二象限
D.复平面内,实数轴上的点对应的复数是实数
【分析】根据已知条件,结合复数的乘法运算法则,以及共轭复数的概念和几何含义,即可求解.
【解答】解:=,故A选项正确,
复数z=4﹣2i的虚部为﹣2,故B选项错误,
∵z=(2+i)2=2i,
∴,
∴复平面内对应的点(0,故C选项错误,
∵复平面内,实数轴上对应的点的纵坐标为0,
∴复平面内,实数轴上的点对应的复数是实数.
故选:AD.
15.已知复数(i为虚数单位),则下列说法错误的是( )
A.z的实部为2 B.z的虚部为1 C. D.
【分析】利用复数代数形式的乘除运算化简z,然后逐一核对四个选项得答案.
【解答】解:====7+i.
所以z=1+i,z的实部为1,|z|==.
观察选项,A、C选项符合题意.
故选:AC.
16.设有下面四个命题:
A.若复数z满足∈R,则z∈R;
B.若复数z满足z2∈R,则z∈R;
C.若复数z1,z2满足z1z2∈R,则z1=;
D.若复数z∈R,则∈R.
其中正确的命题是( )
A.A B.B C.C D.D
【分析】根据复数的基本概念和基本运算判断即可.
【解答】解:对于A,复数z满足,则z=,所以A对;
对于B,当z=i时,z2=﹣1∈R,但z R;
对于C,当z7=i,z2=2i,z3z2=﹣2∈R,但z2≠,所以C错;
对于D,令z=a+bi∈R,于是,所以D对.
故选:AD.
17.下列命题正确的( )
A.若复数z=(1﹣i)(2﹣i),则
B.若z1=2﹣i,z2=1﹣3i,则复数z1﹣z2的虚部是2i
C.若|z﹣1|=2,则|z﹣1﹣3i|的最小值为1
D.已知k∈R,若关于x的方程x2+(k+2i)x+2+ki=0有实数根,则实根必为
【分析】根据复数模运算公式可判断A;根据复数减法运算可判断B;根据复数几何意义可判断C;
设x为实数,结合x2+(k+2i)x+2+ki=0,进行计算,可判断D.
【解答】解:z=(1﹣i)(2﹣i)=3﹣3i,则,∴A对;
若z1=8﹣i,z2=1﹣6i,则复数z1﹣z2=5+2i,其虚部是2;
由|z﹣2|=2,可知复数z对应点在以A(1,
|z﹣4﹣3i|=|z﹣(1+6i)|表示圆A上的点到点B(1,3)的距离,
∴则|z﹣4﹣3i|的最小值为AB﹣2=﹣4=3﹣2=7;
设x为实数,由x2+(k+2i)x+8+ki=0.可得,∴D错.
故选:AC.
18.复数z=2+i的虚部为 1 .
【分析】直接由复数的基本概念得答案.
【解答】解:由复数的基本概念知:
复数z=2+i的虚部为1.
故答案为:5.
19.设复数z1,z2满足z1z2+2i z1﹣2i z2+1=0.
(1)若z1,z2满足,求z1,z2;
(2)若z1,z2是实系数一元二次方程的两个虚根,求实数p的值;
(3)若,是否存在常数k,使得等式|z2﹣4i|=k恒成立,若存在,试求出k
【分析】(1)设z1=a+bi(a,b∈R),由得到z2=a﹣(b+2)i,从而代入z1z2+2i z1﹣2i z2+1=0化简求解;
(2)由题意设z1=+bi,则z2=﹣bi,从而得到2+b2=p,p+2i 2bi+1=0,从而解得;
(3)由题意设z1=a+bi(a,b∈R),则a2+b2=3,化简得z2﹣4i=﹣4i=﹣,从而代入求模即可.
【解答】解:(1)设z1=a+bi(a,b∈R)2=a﹣(b+5)i,
∵z1z2+5i z1﹣2i z4+1=0,
∴(a+bi)(a﹣(b+4)i)+2i(a+bi)﹣2i(a﹣(b+4)i)+1=0,
∴a5+b(b+2)+1﹣8b﹣4﹣2ai=3,
∴a2+b(b+2)+4﹣4b﹣4=3,2a=0,
解得,a=6,
故z1=3i,z5=﹣5i或z1=﹣i,z2=﹣i.
(2)∵z1,z2是实系数一元二次方程的两个虚根,
∴z1+z2=3,z1z5=p,
设z1=+bi6=﹣bi,
由题意得,2+b2=p,p+2i 2bi+3=0,
解得,b=1,p=11;
故p=4或p=11.
(3)设z1=a+bi(a,b∈R)2+b6=3,
由z1z4+2i z1﹣7i z2+1=7得,
z2﹣4i=﹣4i=﹣,
∴|z7﹣4i|=|﹣|
=|3i| ||=3
=4=7;
故k=3.
20.已知i为虚数单位,复数z=2+ai(a∈R),且(1+2i) z为纯虚数.
(1)求z及;
(2)若,求ω的模.
【分析】(1)先化简(1+2i) z,再利用纯虚数的定义求出a的值,从而得到z及.
(2)先利用复数的四则运算求出ω,再利用复数模长的定义求解.
【解答】解:(1)(1+2i) z=(3+2i)(2+ai)=(2﹣2a)+(a+4)i,
∵(4+2i) z为纯虚数,
∴,解得a=1,
∴z=2+i,=4﹣i.
(2)===,
∴ω的模为=.
21.已知复数.
(1)当a∈(﹣2,2)时,求的取值范围;
(2)是否存在实数a,使得z2<0,若存在,求出a的值,说明理由.
【分析】(1)利用复数模的定义求出关于a的表达式,然后利用二次函数的性质求解取值范围即可;
(2)由题意分析可得,z是纯虚数,利用纯虚数的定义列出关于a的关系,求解即可.
【解答】解:(1)因为a∈(﹣2,2),
所以=,
所以的取值范围为;
(2)因为z2<5,所以z是纯虚数,
所以,方程组无解,
故不存在实数a,使得z2<0.
22.如图,在复平面内,复数z对应的点为A.
(Ⅰ)写出复数z及|z|的值;
(Ⅱ)若z1=,求z1,并在复平面内标出z1对应的点B.
【分析】(Ⅰ)由图可知z=1+2i,再由复数模的计算公式求|z|;
(Ⅱ)利用复数代数形式的乘除运算求z1,得到B的坐标,即可在复平面内标出对应的点.
【解答】解:(Ⅰ)由图可知,z=1+2i;
(Ⅱ)∵z1=,∴,
即z1对应的点B为(2,﹣4).
如图:
23.已知z1,z2是实系数一元二次方程的两个虚数根,且z1,z2满足方程2z1+(1﹣i)z2=3+5i.
(1)求z1和z2;
(2)写出一个以z1和z2为根的实系数一元二次方程.
【分析】(1)根据题意设z1=a+bi,z2=a﹣bi,代入2z1+(1﹣i)z2=3+5i,得到关于a,b的方程,再求出a,b,即可可解决此问题.
(2)利用根与系数关系,即可解决此问题.
【解答】解:(1)根据题意,设z1=a+bi,z2=a﹣bi,代入4z1+(1﹣i)z7=3+5i中,
得6a+2bi+(1﹣i)(a﹣bi)=2+5i,整理得3a﹣b+(b﹣a)i=3+5i,
∴,解得,
∴z1=4+3i,z2=4﹣7i;
(2)∵z1+z2=5+9i+4﹣7i=8;z1 z2=(4+9i)(8﹣9i)=97,
∴以z1和z4为根的实系数一元二次方程为x2﹣8x+97=8.
第1页(共1页)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
