黑龙江省大庆市第四十四中学2021-2022学年七年级(五四学制)上学期期末考试数学试题(Word版无答案)
文档属性
| 名称 | 黑龙江省大庆市第四十四中学2021-2022学年七年级(五四学制)上学期期末考试数学试题(Word版无答案) | 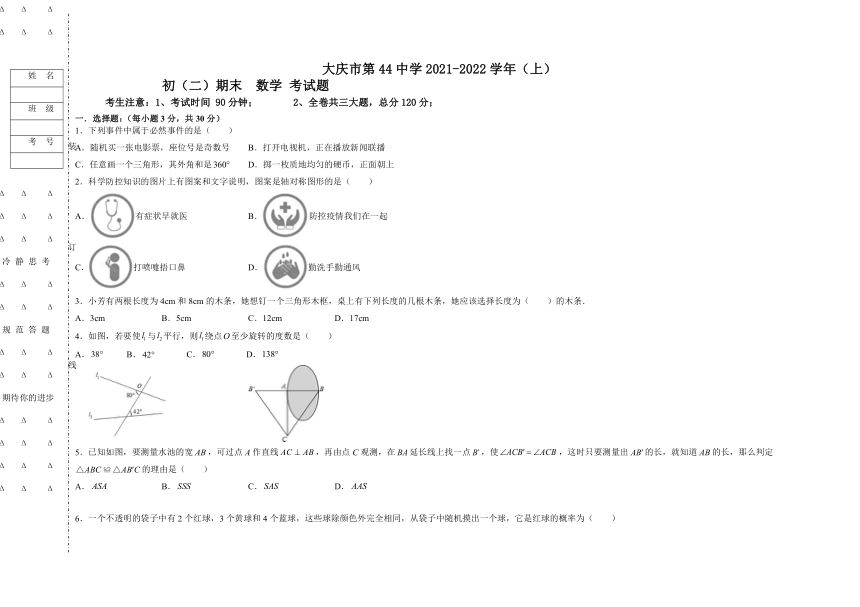 | |
| 格式 | zip | ||
| 文件大小 | 490.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-05 14:11:22 | ||
图片预览

文档简介
大庆市第44中学2021-2022学年(上)
初(二)期末 数学 考试题
考生注意:1、考试时间 90分钟; 2、全卷共三大题,总分120分;
一.选择题:(每小题3分,共30分)
1.下列事件中属于必然事件的是( )
A.随机买一张电影票,座位号是奇数号 B.打开电视机,正在播放新闻联播
C.任意画一个三角形,其外角和是 D.掷一枚质地均匀的硬币,正面朝上
2.科学防控知识的图片上有图案和文字说明,图案是轴对称图形的是( )
A.有症状早就医 B.防控疫情我们在一起
C.打喷嚏捂口鼻 D.勤洗手勤通风
3.小芳有两根长度为4cm和8cm的木条,她想钉一个三角形木框,桌上有下列长度的几根木条,她应该选择长度为( )的木条.
A.3cm B.5cm C.12cm D.17cm
4.如图,若要使与平行,则绕点至少旋转的度数是( )
A. B. C. D.
5.已知如图,要测量水池的宽,可过点A作直线,再由点C观测,在延长线上找一点,使,这时只要测量出的长,就知道的长,那么判定的理由是( )
A. B. C. D.
6.一个不透明的袋子中有2个红球,3个黄球和4个蓝球,这些球除颜色外完全相同,从袋子中随机摸出一个球,它是红球的概率为( )
A. B. C. D.
7.在联合会上,有A、B、C三名选手站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在△ABC的( )
A.三边中线的交点 B.三条角平分线的交点
C.三边垂直平分线的交点 D.三边上高的交点
8.下列有四个结论,其中正确的是( )
①若,则只能是; ②若的运算结果中不含项,则
③若,,则 ④若,,则可表示为
A.①②③④ B.②③④ C.①③④ D.②④
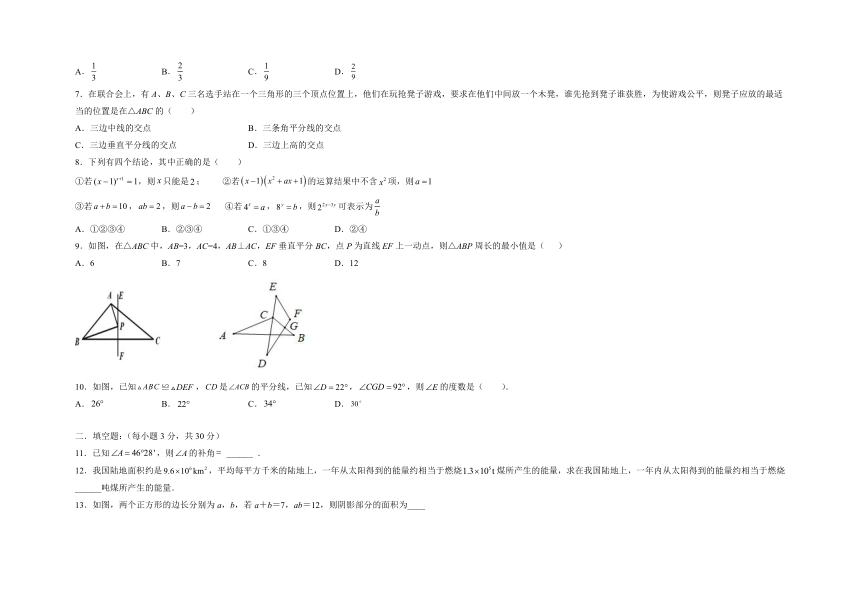
9.如图,在△ABC中,AB=3,AC=4,AB⊥AC,EF垂直平分BC,点P为直线EF上一动点,则△ABP周长的最小值是( )
A.6 B.7 C.8 D.12
10.如图,已知≌,是的平分线,已知,,则的度数是( ).
A. B. C. D.
二.填空题:(每小题3分,共30分)
11.已知,则的补角 ______ .
12.我国陆地面积约是,平均每平方千米的陆地上,一年从太阳得到的能量约相当于燃烧煤所产生的能量,求在我国陆地上,一年内从太阳得到的能量约相当于燃烧______吨煤所产生的能量.
13.如图,两个正方形的边长分别为a,b,若a+b=7,ab=12,则阴影部分的面积为____
14.如图,,,,则∠CAD的度数为____________.
15.如图,一个可以自由转动的圆形转盘,转盘按1:2:3:4的比例分成A,B,C,D四个扇形区域,指针的位置固定,任意转动转盘1次,则停止后指针恰好落在B区域的概率为_______.
16.如图,将△ABC折叠,使点B落在AC边的中点D处,折痕为MN,若BC=3,AC=2,则△CDN的周长为 .
17.如图,在中,已知点、、分别是、、的中点,且,则三角形_________.
18.等腰三角形一腰上的高与另一腰的夹角为40°,则它的底角为 。
19.在一条可以折叠的数轴上,A,B表示的数分别是-16,9,如图,以点C为折点,将此数轴向右对折,若点A在点B的右边,且AB=1,则C点表示的数是_______.
20.如图,直线PQ经过Rt△ABC的直角顶点C,△ABC的边上有两个动点D、E,点D以1cm/s的速度从点A出发,沿AC→CB移动到点B,点E以3cm/s的速度从点B出发,沿BC→CA移动到点A,两动点中有一个点到达终点后另一个点继续移动到终点.过点D、E分别作DM⊥PQ,EN⊥PQ,垂足分别为点M、N,若AC=6cm,BC=8cm,设运动时间为t,则当t=__________ s时,以点D、M、C为顶点的三角形与以点E、N、C为顶点的三角形全等.
3.解答题:(60分)
21.计算:(每小题5分,共15分)
(1);
(2);
(3);
22.(8分)如图,在10×10的正方形网格中,每个小正方形的边长都为1,网格中有一个格点三角形ABC(三角形的顶点都在网格格点上).
(1)在图中画出△ABC关于直线l对称的△A′B′C′(要求:点A与点A′、点B与点B′、点C与点C′相对应);
(2)在(1)的结果下,设AB交直线l于点D,连接AB′,求四边形AB′CD的面积.
23.(8分)已知:整式,整式.
(1)若,求a的值;
(2)若可以分解为,求A+B.
24.(8分)如图,在△ABC中,AF平分∠BAC,AC的垂直平分线交BC于点E,∠B=70°,∠FAE=19°,求∠C的度数。
25.(9分)“一方有难,八方支援”.2020年初武汉受到新型冠状肺炎影响,沈阳某医院准备从甲、乙、丙三位医生和A,B,C三名护士中选取一位医生和一名护士支援武汉.用树状图求恰好选中医生甲和护士A的概率.
26.(12分)(问题)在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAF=60°,试探究图1中线段BE、EF、FD之间的数量关系.
(1)(探索)有同学认为:延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,则可得到BE、EF、FD之间的数量关系是 .
(2)(延伸)在四边形ABCD中如图2,AB=AD,∠B+∠D=180°,E、F分别是BC、CD上的点,∠EAF=∠BAD,上述结论是否仍然成立?说明理由.
(3)(构造运用)如图3,在某次搜救行动中,甲艇在指挥中心(O处)北偏西30°的A处,乙艇在O点的南偏东70°的B处,且AO=BO,接到行动指令后,甲艇向正东方向以60海里/小时的速度前进,乙艇沿北偏东50°的方向以80海里/小时的速度前进1.5小时后,甲、乙两艇分别到达E,F处,∠EOF=70°,试求此时甲、乙两艇之间的距离.
Δ Δ Δ
Δ Δ Δ
姓 名
班 级
考 号
Δ Δ Δ
Δ Δ Δ
Δ Δ Δ
冷 静 思 考
Δ Δ Δ
Δ Δ Δ
规 范 答 题
Δ Δ Δ
Δ Δ Δ
期待你的进步
Δ Δ Δ
Δ Δ Δ
Δ Δ Δ
Δ Δ Δ
装 订 线
初(二)期末 数学 考试题
考生注意:1、考试时间 90分钟; 2、全卷共三大题,总分120分;
一.选择题:(每小题3分,共30分)
1.下列事件中属于必然事件的是( )
A.随机买一张电影票,座位号是奇数号 B.打开电视机,正在播放新闻联播
C.任意画一个三角形,其外角和是 D.掷一枚质地均匀的硬币,正面朝上
2.科学防控知识的图片上有图案和文字说明,图案是轴对称图形的是( )
A.有症状早就医 B.防控疫情我们在一起
C.打喷嚏捂口鼻 D.勤洗手勤通风
3.小芳有两根长度为4cm和8cm的木条,她想钉一个三角形木框,桌上有下列长度的几根木条,她应该选择长度为( )的木条.
A.3cm B.5cm C.12cm D.17cm
4.如图,若要使与平行,则绕点至少旋转的度数是( )
A. B. C. D.
5.已知如图,要测量水池的宽,可过点A作直线,再由点C观测,在延长线上找一点,使,这时只要测量出的长,就知道的长,那么判定的理由是( )
A. B. C. D.
6.一个不透明的袋子中有2个红球,3个黄球和4个蓝球,这些球除颜色外完全相同,从袋子中随机摸出一个球,它是红球的概率为( )
A. B. C. D.
7.在联合会上,有A、B、C三名选手站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在△ABC的( )
A.三边中线的交点 B.三条角平分线的交点
C.三边垂直平分线的交点 D.三边上高的交点
8.下列有四个结论,其中正确的是( )
①若,则只能是; ②若的运算结果中不含项,则
③若,,则 ④若,,则可表示为
A.①②③④ B.②③④ C.①③④ D.②④
9.如图,在△ABC中,AB=3,AC=4,AB⊥AC,EF垂直平分BC,点P为直线EF上一动点,则△ABP周长的最小值是( )
A.6 B.7 C.8 D.12
10.如图,已知≌,是的平分线,已知,,则的度数是( ).
A. B. C. D.
二.填空题:(每小题3分,共30分)
11.已知,则的补角 ______ .
12.我国陆地面积约是,平均每平方千米的陆地上,一年从太阳得到的能量约相当于燃烧煤所产生的能量,求在我国陆地上,一年内从太阳得到的能量约相当于燃烧______吨煤所产生的能量.
13.如图,两个正方形的边长分别为a,b,若a+b=7,ab=12,则阴影部分的面积为____
14.如图,,,,则∠CAD的度数为____________.
15.如图,一个可以自由转动的圆形转盘,转盘按1:2:3:4的比例分成A,B,C,D四个扇形区域,指针的位置固定,任意转动转盘1次,则停止后指针恰好落在B区域的概率为_______.
16.如图,将△ABC折叠,使点B落在AC边的中点D处,折痕为MN,若BC=3,AC=2,则△CDN的周长为 .
17.如图,在中,已知点、、分别是、、的中点,且,则三角形_________.
18.等腰三角形一腰上的高与另一腰的夹角为40°,则它的底角为 。
19.在一条可以折叠的数轴上,A,B表示的数分别是-16,9,如图,以点C为折点,将此数轴向右对折,若点A在点B的右边,且AB=1,则C点表示的数是_______.
20.如图,直线PQ经过Rt△ABC的直角顶点C,△ABC的边上有两个动点D、E,点D以1cm/s的速度从点A出发,沿AC→CB移动到点B,点E以3cm/s的速度从点B出发,沿BC→CA移动到点A,两动点中有一个点到达终点后另一个点继续移动到终点.过点D、E分别作DM⊥PQ,EN⊥PQ,垂足分别为点M、N,若AC=6cm,BC=8cm,设运动时间为t,则当t=__________ s时,以点D、M、C为顶点的三角形与以点E、N、C为顶点的三角形全等.
3.解答题:(60分)
21.计算:(每小题5分,共15分)
(1);
(2);
(3);
22.(8分)如图,在10×10的正方形网格中,每个小正方形的边长都为1,网格中有一个格点三角形ABC(三角形的顶点都在网格格点上).
(1)在图中画出△ABC关于直线l对称的△A′B′C′(要求:点A与点A′、点B与点B′、点C与点C′相对应);
(2)在(1)的结果下,设AB交直线l于点D,连接AB′,求四边形AB′CD的面积.
23.(8分)已知:整式,整式.
(1)若,求a的值;
(2)若可以分解为,求A+B.
24.(8分)如图,在△ABC中,AF平分∠BAC,AC的垂直平分线交BC于点E,∠B=70°,∠FAE=19°,求∠C的度数。
25.(9分)“一方有难,八方支援”.2020年初武汉受到新型冠状肺炎影响,沈阳某医院准备从甲、乙、丙三位医生和A,B,C三名护士中选取一位医生和一名护士支援武汉.用树状图求恰好选中医生甲和护士A的概率.
26.(12分)(问题)在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAF=60°,试探究图1中线段BE、EF、FD之间的数量关系.
(1)(探索)有同学认为:延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,则可得到BE、EF、FD之间的数量关系是 .
(2)(延伸)在四边形ABCD中如图2,AB=AD,∠B+∠D=180°,E、F分别是BC、CD上的点,∠EAF=∠BAD,上述结论是否仍然成立?说明理由.
(3)(构造运用)如图3,在某次搜救行动中,甲艇在指挥中心(O处)北偏西30°的A处,乙艇在O点的南偏东70°的B处,且AO=BO,接到行动指令后,甲艇向正东方向以60海里/小时的速度前进,乙艇沿北偏东50°的方向以80海里/小时的速度前进1.5小时后,甲、乙两艇分别到达E,F处,∠EOF=70°,试求此时甲、乙两艇之间的距离.
Δ Δ Δ
Δ Δ Δ
姓 名
班 级
考 号
Δ Δ Δ
Δ Δ Δ
Δ Δ Δ
冷 静 思 考
Δ Δ Δ
Δ Δ Δ
规 范 答 题
Δ Δ Δ
Δ Δ Δ
期待你的进步
Δ Δ Δ
Δ Δ Δ
Δ Δ Δ
Δ Δ Δ
装 订 线
同课章节目录
