北师大版数学八年级上册《第五章 二元一次方程组》单元测试(word版含解析)
文档属性
| 名称 | 北师大版数学八年级上册《第五章 二元一次方程组》单元测试(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 108.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-05 17:56:43 | ||
图片预览


文档简介
北师大版数学八年级上册《第五章 二元一次方程组》单元测试
一 、单选题(本大题共15小题,共45分)
1.已知有含盐与含盐的盐水,若配制含盐的盐水千克,设需含盐的盐水千克,含盐的盐水千克,则下列方程组中正确的是
A. B.
C. D.
2.一件商品如果按定价打九折出售可以盈利,如果按定价打八折出售可以盈利元,求此商品的进价、定价分别为多少元?若设此商品的进价为元,定价为元,则可列方程组为
A. B.
C. D.
3.机械厂加工车间有名工人,平均每人每天加工大齿轮个或小齿轮个,已知个大齿轮与个小齿轮配成一套,问需分别安排多少名工人加工大、小齿轮,才能使每天加工的大小齿轮刚好配套?设安排名工人加工大齿轮,安排名工人加工小齿轮,可列方程组为
A. B.
C. D.
4.方程组的解是
A. B. C. D.
5.已知和都是方程的解,则的值是
A. B. C. D.
6.中国清代算书《御制数理精蕴》中有这样一题:“马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两.问马、牛各价几何?”设马每匹x两,牛每头y两,根据题意可列方程组为
A. B.
C. D.
7.小岩打算购买气球装扮学校“毕业典礼”活动会场,气球的种类有笑脸和爱心两种,两种气球的价格不同,但同一种气球的价格相同.由于会场布置需要,购买时以一束(4个气球)为单位,已知第一、二束气球的价格如图所示,则第三束气球的价格为 ( )
A. 19元 B. 18元 C. 16元 D. 15元
8.若以二元一次方程的解为坐标的点都在直线上,则常数
A. B. C. D.
9.如图,已知函数和的图象交于点,则根据图象可知,关于,的二元一次方程组的解是
A. B.
C. D.
10.如图,直线对应的函数表达式是
A. B.
C. D.
11.如果一次函数当自变量的取值范围是时,函数值的取值范围是,那么此函数的解析式是
A. B.
C. 或 D. 或
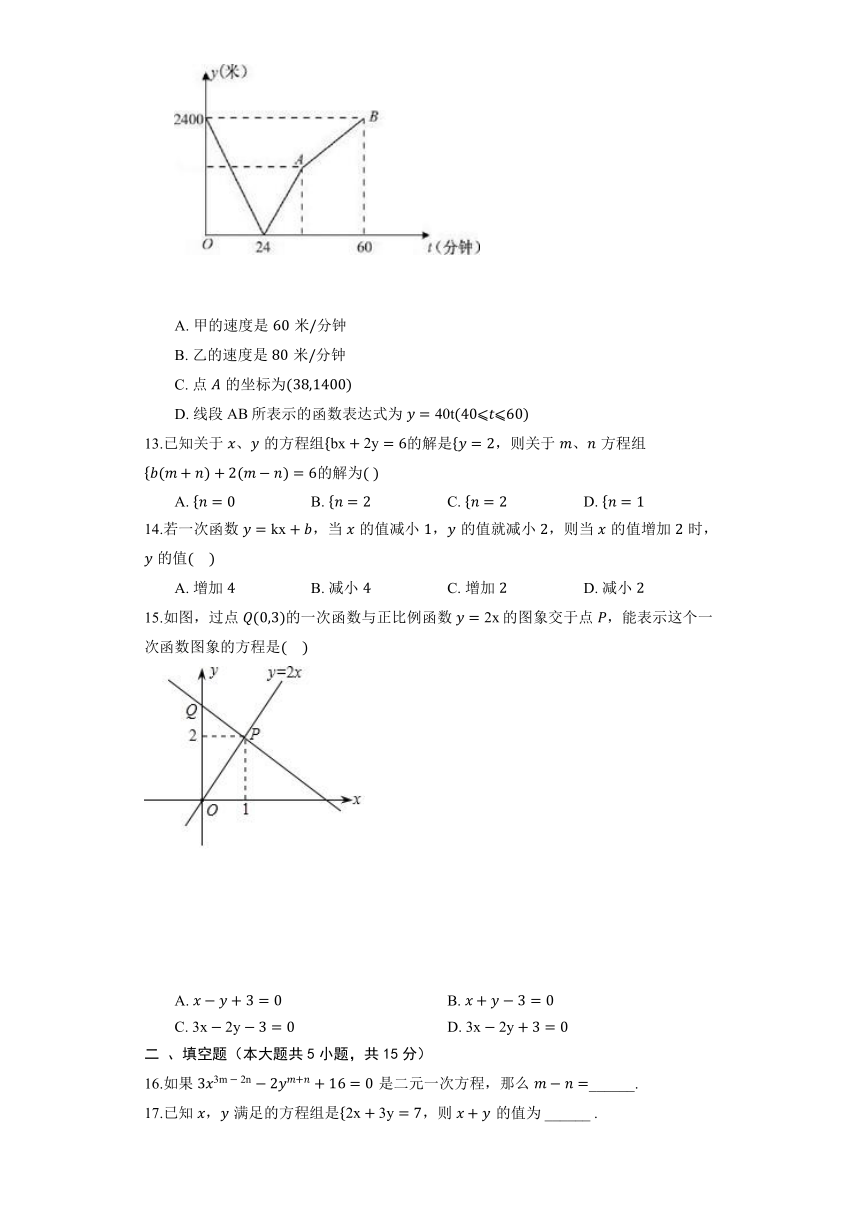
12.学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离米与时间分钟之间的函数关系如图所示,其中说法正确的是
A. 甲的速度是米分钟
B. 乙的速度是米分钟
C. 点的坐标为
D. 线段所表示的函数表达式为
13.已知关于、的方程组的解是,则关于、方程组的解为
A. B. C. D.
14.若一次函数,当的值减小,的值就减小,则当的值增加时,的值
A. 增加 B. 减小 C. 增加 D. 减小
15.如图,过点的一次函数与正比例函数的图象交于点,能表示这个一次函数图象的方程是
A. B.
C. D.
二 、填空题(本大题共5小题,共15分)
16.如果是二元一次方程,那么______.
17.已知,满足的方程组是,则的值为 ______ .
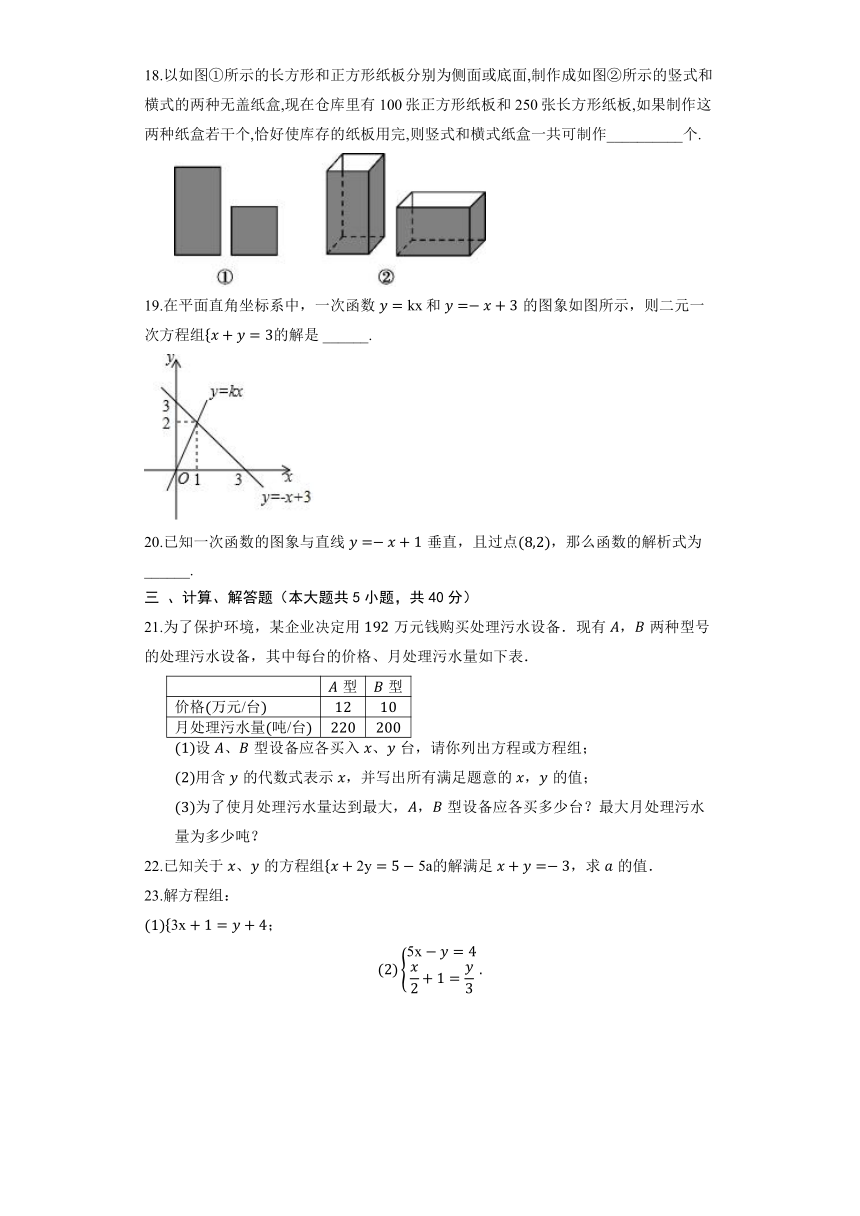
18.以如图①所示的长方形和正方形纸板分别为侧面或底面,制作成如图②所示的竖式和横式的两种无盖纸盒,现在仓库里有100张正方形纸板和250张长方形纸板,如果制作这两种纸盒若干个,恰好使库存的纸板用完,则竖式和横式纸盒一共可制作__________个.
19.在平面直角坐标系中,一次函数和的图象如图所示,则二元一次方程组的解是 ______.
20.已知一次函数的图象与直线垂直,且过点,那么函数的解析式为______.
三 、计算、解答题(本大题共5小题,共40分)
21.为了保护环境,某企业决定用万元钱购买处理污水设备.现有,两种型号的处理污水设备,其中每台的价格、月处理污水量如下表.
型 型
价格万元台
月处理污水量吨台
设、型设备应各买入、台,请你列出方程或方程组;
用含的代数式表示,并写出所有满足题意的,的值;
为了使月处理污水量达到最大,,型设备应各买多少台?最大月处理污水量为多少吨?
22.已知关于、的方程组的解满足,求的值.
23.解方程组:
;
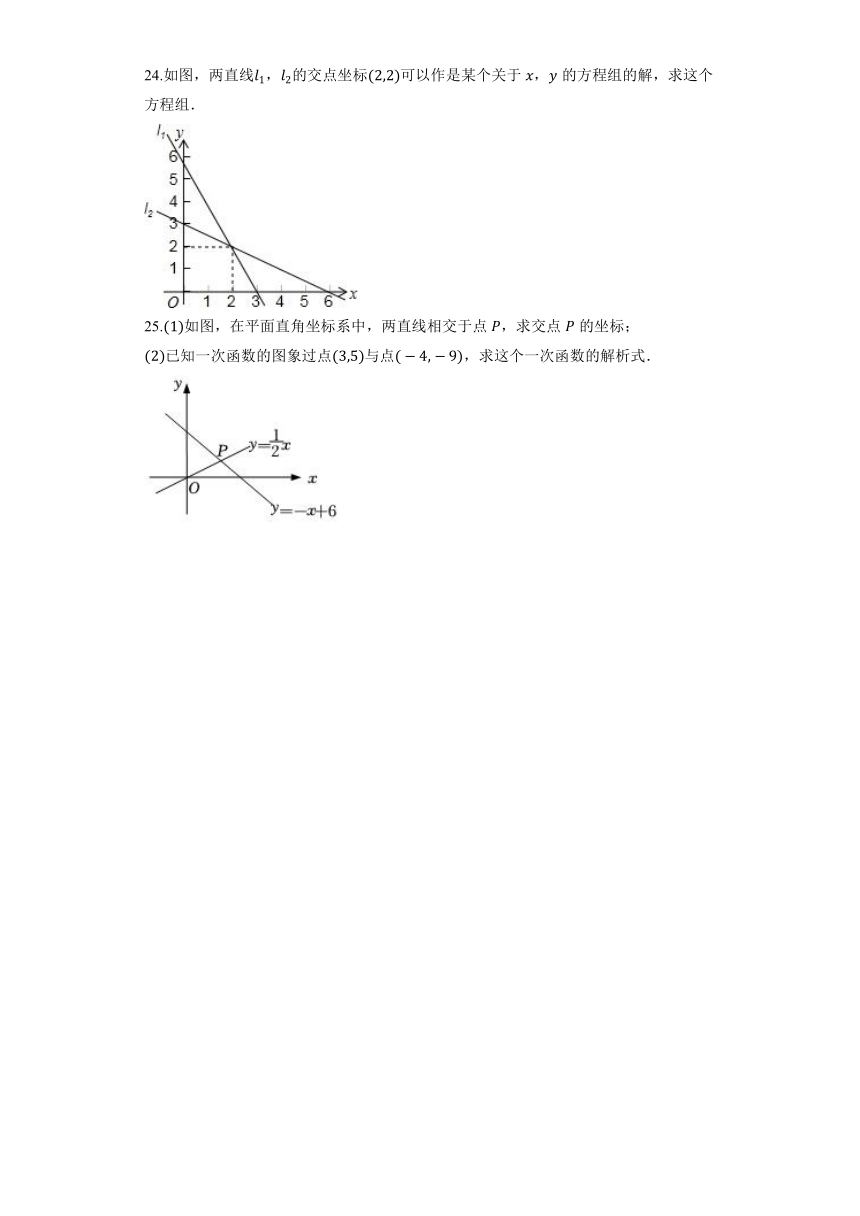
24.如图,两直线,的交点坐标可以作是某个关于,的方程组的解,求这个方程组.
25.如图,在平面直角坐标系中,两直线相交于点,求交点的坐标;
已知一次函数的图象过点与点,求这个一次函数的解析式.
答案和解析
1.【答案】C;
【解析】解:含盐的盐水千克中含盐,含盐的盐水千克中含盐,含盐的盐水千克中含盐,
,
故所列方程组为:,
故选:
易得有个等量关系:含盐的盐水质量含盐的盐水质量;含盐的盐水中的纯盐质量含盐的盐水中的纯盐质量含盐的盐水中的纯盐质量,把相关数值代入即可.
考查列二元一次方程组问题,得到溶液总质量和纯盐总质量的等量关系是解决本题的关键.
2.【答案】B;
【解析】解:设此商品的进价为元,定价为元,
由题意得,
故选:
设此商品的进价为元,定价为元,根据此商品按定价打九折出售可以盈利,如果打八折出售可以盈利元,列出方程组即可.
此题主要考查了由实际问题抽象出二元一次方程组,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列出方程组.
3.【答案】B;
【解析】解:设需安排名工人加工大齿轮,名工人加工小齿轮,根据题意可得:,
故选:
设需安排名工人加工大齿轮,名工人加工小齿轮,根据机械厂加工车间有名工人且加工的大小齿轮刚好配套,即可得出关于,的二元一次方程组,此题得解.
此题主要考查了由实际问题抽象出二元一次方程组,找准等量关系,正确列出二元一次方程组是解答该题的关键.
4.【答案】B;
【解析】解:整理得:,
①②得:,
把代入①得:,
解得:,
方程组的解为:,
故选:
先将原方程组化简整理成,再用①②求出,把代入①求出即可.
此题主要考查了解二元一次方程组的应用,关键是能把二元一次方程组转化成一元一次方程.
5.【答案】A;
【解析】解:根据题意得:,
解得:,
,
故选:
把方程的解代入方程,得到二元一次方程组,可以求出,的值,然后代入求值即可.
此题主要考查了二元一次方程的解,解二元一次方程组,解二元一次方程组的基本思路是消元,把二元方程转化为一元方程是解答该题的关键.
6.【答案】D;
【解析】设马每匹x两,牛每头y两,根据题意可列方程组为:
.
故选:D.
7.【答案】B;
【解析】设笑脸气球元/个,爱心气球元/个,由题意得
∴,∴,故第三束气球的价格为18元.故选B.
8.【答案】B;
【解析】分析
直线解析式乘以后变形和方程是同一个二元一次方程,对应项的系数相等,据此可得答案.
此题主要考查二元一次方程的解与一次函数图象上点的坐标的关系,熟练掌握它们之间的关系是解答该题的关键.
详解
解:因为以二元一次方程的解为坐标的点都在直线上,
所以将变形为:,
对比方程可得,
解得:,
故选B.
9.【答案】A;
【解析】解:函数和的图象交于点,
即,同时满足两个一次函数的解析式.
所以关于,的方程组的解是.
故选:.
由图可知:两个一次函数的交点坐标为;那么交点坐标同时满足两个函数的解析式,而所求的方程组正好是由两个函数的解析式所构成,因此两函数的交点坐标即为方程组的解.
考查了一次函数与二元一次方程组方程组的解就是使方程组中两个方程同时成立的一对未知数的值,而这一对未知数的值也同时满足两个相应的一次函数式,因此方程组的解就是两个相应的一次函数图象的交点坐标.
10.【答案】C;
【解析】
本题要注意利用一次函数的特点,来列出方程组,求出未知数的值从而求得其解析式.
把点,代入直线的方程,用待定系数法求出函数关系式,从而得出结果.
解:设直线对应的函数表达式是,
把,代入,
得,
解得,
故直线对应的函数表达式是.
故选C.
11.【答案】C;
【解析】
此题主要考查了一次函数的性质有关知识,分两种情况讨论:当时,;时,;当时,;时,;据此利用待定系数法求出一次函数解析式即可.
解:设一次函数解析式为,
当时,;时,;
代入解析式得:,
解得,,
函数解析式为;
当时,;时,;
代入解析式得,,
解得,
函数解析式为
故选
12.【答案】D;
【解析】【试题解析】
该题考查了一次函数的应用,路程、速度、时间的关系,用待定系数法确定函数的解析式,属于中考常考题型.
根据图象信息,当分钟时甲乙两人相遇,甲分钟行驶米,根据速度路程时间可得甲的速度;由甲、乙两人的速度和为米分钟,减去甲的速度得出乙的速度,再根据“路程、时间与速度”的关系解答即可;将、两点的坐标代入,利用待定系数法即可求出线段所表示的函数表达式.
解:根据图象信息,当分钟时甲乙两人相遇,甲的速度为米分钟,故选项A不合题意;
甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,分钟时甲乙两人相遇,
甲、乙两人的速度和为米分钟,
乙的速度为米分钟,故选项B不合题意;
乙从图书馆回学校的时间为分钟,
米,
点的坐标为,故选项C不合题意;
设线段所表示的函数表达式为,
,,
解得
线段所表示的函数表达式为,故选项D符合题意.
故选:.
13.【答案】A;
【解析】解:方程组的解是,
方程组的
解方程组得
故选:
由于两个方程的形式相同、常数和对应项的系数都相同,所以两个方程组的解相同.根据解相同,可得含、的二元一次方程组,求解即可.
此题主要考查了二元一次方程组的解法,根据两个方程组的特点,得到解间关系是解决本题的关键.另解决本题亦可先把解代入第一个方程组求出、的值,再把、的值代入第二个方程组,求解关于、的方程组后得结论.
14.【答案】A;
【解析】解:当的值减小,的值就减小,
,
又,
,即,
.
当的值增加时,
,
当的值增加时,的值增加.
故选:.
此题只需根据已知条件分析得到的值,即可求解.
此题主要是能够根据已知条件正确分析得到的值.
15.【答案】B;
【解析】
这道题主要考查了用待定系数法求一次函数的解析式.
设这个一次函数的解析式为,根据这条直线经过点和点,用待定系数法即可得出此一次函数的解析式.
解:设这个一次函数的解析式为.
这条直线经过点和点,
,
解得.
故这个一次函数的解析式为,
即:.
故选B.
16.【答案】;
【解析】解:由题意,得
,
解得,
,
故答案为:
根据二元一次方程的定义求解即可.
此题主要考查了二元一次方程的定义,二元一次方程必须符合以下三个条件:方程中只含有个未知数;含未知数项的最高次数为一次;方程是整式方程.
17.【答案】5;
【解析】解:,
②①得,,
故答案为
将方程组中的两个方程直接相减即可求解.
此题主要考查二元一次方程组的解,熟练掌握二元一次方程组的解法,通过观察方程组中两个方程的特点,灵活计算是解答该题的关键.
18.【答案】70;
【解析】设制作竖式和横式的两种无盖纸盒分别为个、个,
根据题意得
解得
又40+30=70(个),
∴竖式和横式纸盒一共可制作70个.
故答案为70.
19.【答案】;
【解析】解:一次函数和的图象交于点,
二元一次方程组的解是
故答案为:
两个一次函数图象的交点坐标就是两函数组成的方程组的解.
此题主要考查了一次函数与二元一次方程组,关键是掌握二元一次方程组与一次函数的关系.
20.【答案】y=x-6;
【解析】解:设所求的一次函数为,
一次函数的图象与直线垂直,
一次函数经过点
,
,
故答案为
根据两条直线垂直,之间的关系求出,设一次函数为用待定系数法解决.
此题主要考查一次函数的定义、两条直线垂直的乘积为,解决题目的关键是待定系数法.
21.【答案】解:(1)由题意,得
12x+10y=192;
(2)∵12x+10y=192
∴;
∵x,y都是自然数,
∴,
∴,
∴,
∵y是6的倍数,
∴y=0,6,12,18,
∴;;;.
(3)设月污水处理量为W吨,由题意得:
W=220x+200y,
∴W=220(16-y)+200y,
=3520+y,
∵k=>0,
∴W随y的增大而增大,
∴当y=18,x=1时,
∴W最大=3520+300=3820吨
∴当购买A型1台,B型18台时月处理污水量最大为3820吨.;
【解析】
运用型机器的单价型机器的数量型机器的单价型机器的数量就可以得出总价万元建立方程就可以了;
先移项,将不含的项移到等号的右边,再将的系数化为,再根据、为自然数就可以满足条件的、的值;
先求出的取值范围,设月污水处理量为吨,用表示出,根据一次函数的性质可以求出其值.
此题主要考查了列二元一次方程解实际问题的运用,在特定条件下二元一次方程的解的运用,运用一次函数的解析式的性质求最值的而运用.解答时根据取值范围求、的值是关键.
22.【答案】解:,
①+②,得
3x+3y=6-3a,
∴x+y=2-a,
∵x+y=-3,
∴2-a=-3,
∴a=5.;
【解析】
①②可得,然后列出关于的方程求解即可.
此题主要考查了二元一次方程组的特殊解法,在求二元一次方程组中两个未知数的和或差的时候,有时可以采用把两个方程直接相加或相减的方法,而不必求出两个未知数的具体值.
23.【答案】(1),
解:由②得:y=3x-3③,
将③代入①得2x+9x-9=13,
解得x=2,
将x=2代入③得:y=3,
∴原方程的解为;
(2),
解:由①得:③,
将③代入①得:,
解得x=2,
将x=2代入③得:y=6,
∴原方程的解为.;
【解析】
方程组利用代入消元法求出解即可;
方程组利用加减消元法求出解即可.
此题主要考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
24.【答案】解:由图知:两函数的图象经过点(2,2),(3,0),(0,3),
可求得两直线的解析式为:y=-2x+6和y=-x+3,
因而直线,的交点坐标可以看作方程组即的解.;
【解析】
因为函数图象交点坐标为两函数解析式组成的方程组的解.因此本题应该先用待定系数法求出两条直线的解析式,联立两直线解析式所组成的方程组即为所求的方程组.
此题主要考查一次函数和方程组问题,在同一平面直角坐标系中,两个一次函数图象的交点坐标就是相应的二元一次方程组的解.反过来,以二元一次方程组的解为坐标的点,一定是相应的两个一次函数的图象的交点.
25.【答案】解:(1)解方程组得
∴交点P的坐标为(4,2);
(2)设一次函数的解析式为y=kx+b(k≠0).
∵它的图象经过点(3,5),(-4,-9),
∴
解得
∴这个一次函数的解析式为y=2x-1.;
【解析】
由两个一次函数表达式组成的方程组的解就是两条直线的交点的坐标;
设一次函数解析式为把两个已知点的坐标代入得到、的方程组,然后解方程组即可.
此题主要考查了两直线相交或平行问题,待定系数法求函数解析式,两直线的交点就是两直线解析式所组成方程组的解.也考查了解二元一次方程组.
一 、单选题(本大题共15小题,共45分)
1.已知有含盐与含盐的盐水,若配制含盐的盐水千克,设需含盐的盐水千克,含盐的盐水千克,则下列方程组中正确的是
A. B.
C. D.
2.一件商品如果按定价打九折出售可以盈利,如果按定价打八折出售可以盈利元,求此商品的进价、定价分别为多少元?若设此商品的进价为元,定价为元,则可列方程组为
A. B.
C. D.
3.机械厂加工车间有名工人,平均每人每天加工大齿轮个或小齿轮个,已知个大齿轮与个小齿轮配成一套,问需分别安排多少名工人加工大、小齿轮,才能使每天加工的大小齿轮刚好配套?设安排名工人加工大齿轮,安排名工人加工小齿轮,可列方程组为
A. B.
C. D.
4.方程组的解是
A. B. C. D.
5.已知和都是方程的解,则的值是
A. B. C. D.
6.中国清代算书《御制数理精蕴》中有这样一题:“马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两.问马、牛各价几何?”设马每匹x两,牛每头y两,根据题意可列方程组为
A. B.
C. D.
7.小岩打算购买气球装扮学校“毕业典礼”活动会场,气球的种类有笑脸和爱心两种,两种气球的价格不同,但同一种气球的价格相同.由于会场布置需要,购买时以一束(4个气球)为单位,已知第一、二束气球的价格如图所示,则第三束气球的价格为 ( )
A. 19元 B. 18元 C. 16元 D. 15元
8.若以二元一次方程的解为坐标的点都在直线上,则常数
A. B. C. D.
9.如图,已知函数和的图象交于点,则根据图象可知,关于,的二元一次方程组的解是
A. B.
C. D.
10.如图,直线对应的函数表达式是
A. B.
C. D.
11.如果一次函数当自变量的取值范围是时,函数值的取值范围是,那么此函数的解析式是
A. B.
C. 或 D. 或
12.学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离米与时间分钟之间的函数关系如图所示,其中说法正确的是
A. 甲的速度是米分钟
B. 乙的速度是米分钟
C. 点的坐标为
D. 线段所表示的函数表达式为
13.已知关于、的方程组的解是,则关于、方程组的解为
A. B. C. D.
14.若一次函数,当的值减小,的值就减小,则当的值增加时,的值
A. 增加 B. 减小 C. 增加 D. 减小
15.如图,过点的一次函数与正比例函数的图象交于点,能表示这个一次函数图象的方程是
A. B.
C. D.
二 、填空题(本大题共5小题,共15分)
16.如果是二元一次方程,那么______.
17.已知,满足的方程组是,则的值为 ______ .
18.以如图①所示的长方形和正方形纸板分别为侧面或底面,制作成如图②所示的竖式和横式的两种无盖纸盒,现在仓库里有100张正方形纸板和250张长方形纸板,如果制作这两种纸盒若干个,恰好使库存的纸板用完,则竖式和横式纸盒一共可制作__________个.
19.在平面直角坐标系中,一次函数和的图象如图所示,则二元一次方程组的解是 ______.
20.已知一次函数的图象与直线垂直,且过点,那么函数的解析式为______.
三 、计算、解答题(本大题共5小题,共40分)
21.为了保护环境,某企业决定用万元钱购买处理污水设备.现有,两种型号的处理污水设备,其中每台的价格、月处理污水量如下表.
型 型
价格万元台
月处理污水量吨台
设、型设备应各买入、台,请你列出方程或方程组;
用含的代数式表示,并写出所有满足题意的,的值;
为了使月处理污水量达到最大,,型设备应各买多少台?最大月处理污水量为多少吨?
22.已知关于、的方程组的解满足,求的值.
23.解方程组:
;
24.如图,两直线,的交点坐标可以作是某个关于,的方程组的解,求这个方程组.
25.如图,在平面直角坐标系中,两直线相交于点,求交点的坐标;
已知一次函数的图象过点与点,求这个一次函数的解析式.
答案和解析
1.【答案】C;
【解析】解:含盐的盐水千克中含盐,含盐的盐水千克中含盐,含盐的盐水千克中含盐,
,
故所列方程组为:,
故选:
易得有个等量关系:含盐的盐水质量含盐的盐水质量;含盐的盐水中的纯盐质量含盐的盐水中的纯盐质量含盐的盐水中的纯盐质量,把相关数值代入即可.
考查列二元一次方程组问题,得到溶液总质量和纯盐总质量的等量关系是解决本题的关键.
2.【答案】B;
【解析】解:设此商品的进价为元,定价为元,
由题意得,
故选:
设此商品的进价为元,定价为元,根据此商品按定价打九折出售可以盈利,如果打八折出售可以盈利元,列出方程组即可.
此题主要考查了由实际问题抽象出二元一次方程组,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列出方程组.
3.【答案】B;
【解析】解:设需安排名工人加工大齿轮,名工人加工小齿轮,根据题意可得:,
故选:
设需安排名工人加工大齿轮,名工人加工小齿轮,根据机械厂加工车间有名工人且加工的大小齿轮刚好配套,即可得出关于,的二元一次方程组,此题得解.
此题主要考查了由实际问题抽象出二元一次方程组,找准等量关系,正确列出二元一次方程组是解答该题的关键.
4.【答案】B;
【解析】解:整理得:,
①②得:,
把代入①得:,
解得:,
方程组的解为:,
故选:
先将原方程组化简整理成,再用①②求出,把代入①求出即可.
此题主要考查了解二元一次方程组的应用,关键是能把二元一次方程组转化成一元一次方程.
5.【答案】A;
【解析】解:根据题意得:,
解得:,
,
故选:
把方程的解代入方程,得到二元一次方程组,可以求出,的值,然后代入求值即可.
此题主要考查了二元一次方程的解,解二元一次方程组,解二元一次方程组的基本思路是消元,把二元方程转化为一元方程是解答该题的关键.
6.【答案】D;
【解析】设马每匹x两,牛每头y两,根据题意可列方程组为:
.
故选:D.
7.【答案】B;
【解析】设笑脸气球元/个,爱心气球元/个,由题意得
∴,∴,故第三束气球的价格为18元.故选B.
8.【答案】B;
【解析】分析
直线解析式乘以后变形和方程是同一个二元一次方程,对应项的系数相等,据此可得答案.
此题主要考查二元一次方程的解与一次函数图象上点的坐标的关系,熟练掌握它们之间的关系是解答该题的关键.
详解
解:因为以二元一次方程的解为坐标的点都在直线上,
所以将变形为:,
对比方程可得,
解得:,
故选B.
9.【答案】A;
【解析】解:函数和的图象交于点,
即,同时满足两个一次函数的解析式.
所以关于,的方程组的解是.
故选:.
由图可知:两个一次函数的交点坐标为;那么交点坐标同时满足两个函数的解析式,而所求的方程组正好是由两个函数的解析式所构成,因此两函数的交点坐标即为方程组的解.
考查了一次函数与二元一次方程组方程组的解就是使方程组中两个方程同时成立的一对未知数的值,而这一对未知数的值也同时满足两个相应的一次函数式,因此方程组的解就是两个相应的一次函数图象的交点坐标.
10.【答案】C;
【解析】
本题要注意利用一次函数的特点,来列出方程组,求出未知数的值从而求得其解析式.
把点,代入直线的方程,用待定系数法求出函数关系式,从而得出结果.
解:设直线对应的函数表达式是,
把,代入,
得,
解得,
故直线对应的函数表达式是.
故选C.
11.【答案】C;
【解析】
此题主要考查了一次函数的性质有关知识,分两种情况讨论:当时,;时,;当时,;时,;据此利用待定系数法求出一次函数解析式即可.
解:设一次函数解析式为,
当时,;时,;
代入解析式得:,
解得,,
函数解析式为;
当时,;时,;
代入解析式得,,
解得,
函数解析式为
故选
12.【答案】D;
【解析】【试题解析】
该题考查了一次函数的应用,路程、速度、时间的关系,用待定系数法确定函数的解析式,属于中考常考题型.
根据图象信息,当分钟时甲乙两人相遇,甲分钟行驶米,根据速度路程时间可得甲的速度;由甲、乙两人的速度和为米分钟,减去甲的速度得出乙的速度,再根据“路程、时间与速度”的关系解答即可;将、两点的坐标代入,利用待定系数法即可求出线段所表示的函数表达式.
解:根据图象信息,当分钟时甲乙两人相遇,甲的速度为米分钟,故选项A不合题意;
甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,分钟时甲乙两人相遇,
甲、乙两人的速度和为米分钟,
乙的速度为米分钟,故选项B不合题意;
乙从图书馆回学校的时间为分钟,
米,
点的坐标为,故选项C不合题意;
设线段所表示的函数表达式为,
,,
解得
线段所表示的函数表达式为,故选项D符合题意.
故选:.
13.【答案】A;
【解析】解:方程组的解是,
方程组的
解方程组得
故选:
由于两个方程的形式相同、常数和对应项的系数都相同,所以两个方程组的解相同.根据解相同,可得含、的二元一次方程组,求解即可.
此题主要考查了二元一次方程组的解法,根据两个方程组的特点,得到解间关系是解决本题的关键.另解决本题亦可先把解代入第一个方程组求出、的值,再把、的值代入第二个方程组,求解关于、的方程组后得结论.
14.【答案】A;
【解析】解:当的值减小,的值就减小,
,
又,
,即,
.
当的值增加时,
,
当的值增加时,的值增加.
故选:.
此题只需根据已知条件分析得到的值,即可求解.
此题主要是能够根据已知条件正确分析得到的值.
15.【答案】B;
【解析】
这道题主要考查了用待定系数法求一次函数的解析式.
设这个一次函数的解析式为,根据这条直线经过点和点,用待定系数法即可得出此一次函数的解析式.
解:设这个一次函数的解析式为.
这条直线经过点和点,
,
解得.
故这个一次函数的解析式为,
即:.
故选B.
16.【答案】;
【解析】解:由题意,得
,
解得,
,
故答案为:
根据二元一次方程的定义求解即可.
此题主要考查了二元一次方程的定义,二元一次方程必须符合以下三个条件:方程中只含有个未知数;含未知数项的最高次数为一次;方程是整式方程.
17.【答案】5;
【解析】解:,
②①得,,
故答案为
将方程组中的两个方程直接相减即可求解.
此题主要考查二元一次方程组的解,熟练掌握二元一次方程组的解法,通过观察方程组中两个方程的特点,灵活计算是解答该题的关键.
18.【答案】70;
【解析】设制作竖式和横式的两种无盖纸盒分别为个、个,
根据题意得
解得
又40+30=70(个),
∴竖式和横式纸盒一共可制作70个.
故答案为70.
19.【答案】;
【解析】解:一次函数和的图象交于点,
二元一次方程组的解是
故答案为:
两个一次函数图象的交点坐标就是两函数组成的方程组的解.
此题主要考查了一次函数与二元一次方程组,关键是掌握二元一次方程组与一次函数的关系.
20.【答案】y=x-6;
【解析】解:设所求的一次函数为,
一次函数的图象与直线垂直,
一次函数经过点
,
,
故答案为
根据两条直线垂直,之间的关系求出,设一次函数为用待定系数法解决.
此题主要考查一次函数的定义、两条直线垂直的乘积为,解决题目的关键是待定系数法.
21.【答案】解:(1)由题意,得
12x+10y=192;
(2)∵12x+10y=192
∴;
∵x,y都是自然数,
∴,
∴,
∴,
∵y是6的倍数,
∴y=0,6,12,18,
∴;;;.
(3)设月污水处理量为W吨,由题意得:
W=220x+200y,
∴W=220(16-y)+200y,
=3520+y,
∵k=>0,
∴W随y的增大而增大,
∴当y=18,x=1时,
∴W最大=3520+300=3820吨
∴当购买A型1台,B型18台时月处理污水量最大为3820吨.;
【解析】
运用型机器的单价型机器的数量型机器的单价型机器的数量就可以得出总价万元建立方程就可以了;
先移项,将不含的项移到等号的右边,再将的系数化为,再根据、为自然数就可以满足条件的、的值;
先求出的取值范围,设月污水处理量为吨,用表示出,根据一次函数的性质可以求出其值.
此题主要考查了列二元一次方程解实际问题的运用,在特定条件下二元一次方程的解的运用,运用一次函数的解析式的性质求最值的而运用.解答时根据取值范围求、的值是关键.
22.【答案】解:,
①+②,得
3x+3y=6-3a,
∴x+y=2-a,
∵x+y=-3,
∴2-a=-3,
∴a=5.;
【解析】
①②可得,然后列出关于的方程求解即可.
此题主要考查了二元一次方程组的特殊解法,在求二元一次方程组中两个未知数的和或差的时候,有时可以采用把两个方程直接相加或相减的方法,而不必求出两个未知数的具体值.
23.【答案】(1),
解:由②得:y=3x-3③,
将③代入①得2x+9x-9=13,
解得x=2,
将x=2代入③得:y=3,
∴原方程的解为;
(2),
解:由①得:③,
将③代入①得:,
解得x=2,
将x=2代入③得:y=6,
∴原方程的解为.;
【解析】
方程组利用代入消元法求出解即可;
方程组利用加减消元法求出解即可.
此题主要考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
24.【答案】解:由图知:两函数的图象经过点(2,2),(3,0),(0,3),
可求得两直线的解析式为:y=-2x+6和y=-x+3,
因而直线,的交点坐标可以看作方程组即的解.;
【解析】
因为函数图象交点坐标为两函数解析式组成的方程组的解.因此本题应该先用待定系数法求出两条直线的解析式,联立两直线解析式所组成的方程组即为所求的方程组.
此题主要考查一次函数和方程组问题,在同一平面直角坐标系中,两个一次函数图象的交点坐标就是相应的二元一次方程组的解.反过来,以二元一次方程组的解为坐标的点,一定是相应的两个一次函数的图象的交点.
25.【答案】解:(1)解方程组得
∴交点P的坐标为(4,2);
(2)设一次函数的解析式为y=kx+b(k≠0).
∵它的图象经过点(3,5),(-4,-9),
∴
解得
∴这个一次函数的解析式为y=2x-1.;
【解析】
由两个一次函数表达式组成的方程组的解就是两条直线的交点的坐标;
设一次函数解析式为把两个已知点的坐标代入得到、的方程组,然后解方程组即可.
此题主要考查了两直线相交或平行问题,待定系数法求函数解析式,两直线的交点就是两直线解析式所组成方程组的解.也考查了解二元一次方程组.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
