2021-2022学年高一上学期数学北师大版必修2 2.2圆的一般方程 课件(共20张PPT)
文档属性
| 名称 | 2021-2022学年高一上学期数学北师大版必修2 2.2圆的一般方程 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 387.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-05 09:54:53 | ||
图片预览







文档简介
(共20张PPT)
2.2 圆的一般方程
乾县第一中学 陈正东
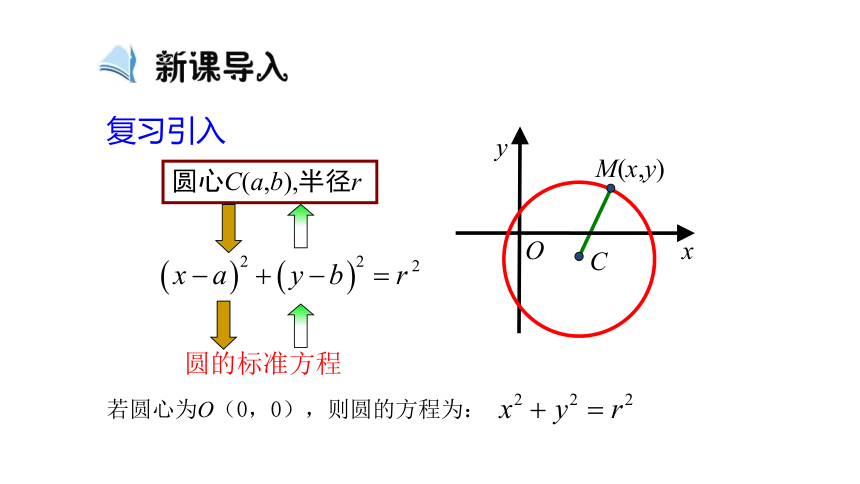
圆的标准方程
x
y
O
C
M(x,y)
圆心C(a,b),半径r
若圆心为O(0,0),则圆的方程为:
复习引入
圆心 (2, -4) ,半径
(1) 圆 (x-2)2+ (y+4)2=2
(2) 圆 (x+1)2+ (y+2)2=m2
圆心 (-1, -2) ,半径|m|
(m≠0)
分别说出下列圆的圆心与半径:
问题引入:
直线方程有五种不同的形式,它们之间可以相互变通,每一种形式都是关于x,y的一次方程,我们学习了圆的标准方程,它的方程形式具备什么特点呢?还有其他形式吗?
x
y
O
C
M(x,y)
展开得
任何一个圆的方程都是二元二次方程
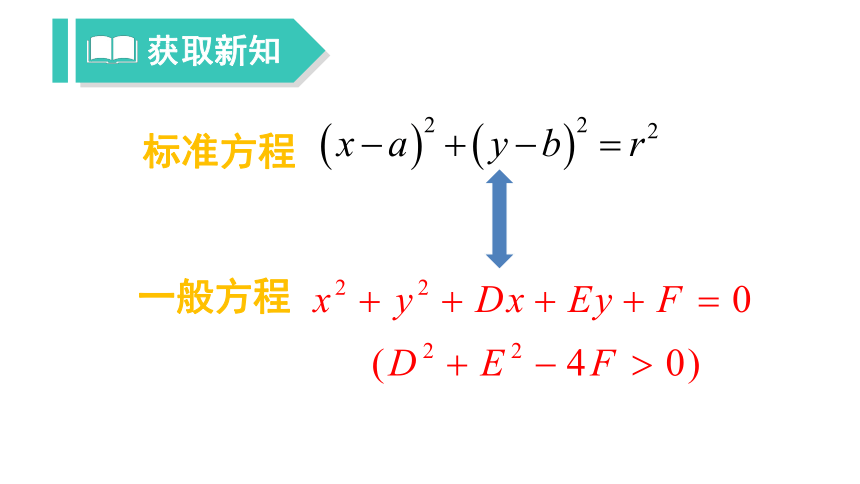
结论:任何一个圆方程可以写成下面形式:
圆的一般方程
1.圆的标准方程
2.是不是任何一个形如
方程表示的曲线是圆呢?
配方得
不一定是圆
以(1,-2)为圆心,以2为半径的圆
配方得
不是圆
结论:
问题提出
(1)当 时,
表示圆,
(2)当 时,
表示点
(3)当 时,
不表示任何图形
圆心
圆的一般方程
配方,得
圆的一般方程
,其中
圆心
注:圆的一般方程的特点:
(2)没有xy项
(3)D2 +E2 -4F>0
(1)x2 , y2 的系数为1
圆的一般方程
圆的标准方程
获取新知
问题探究二当D=0,E=0或F=0时,圆 的位置分别有什么特点?
C
x
O
y
D=0
E=0
F=0
C
x
y
O
C
x
y
O
圆心
(1) x2+y2-2x+4y-4=0
(2) 2x2+2y2-12x+4y=0
(3) x2+2y2-6x+4y-1=0
(4) x2+y2-12x+6y+50=0
(5) x2+y2-3xy+5x+2y=0
是
圆心(1,-2)半径3
是
圆心(3,-1)半径
不是
不是
不是
练习:判断下列方程能否表示圆的方程,若能,写出圆心与半径.
小试牛刀
例1.求过点M(-1,1),且圆心与已知圆C:
x2+y2-4x+6y-3=0
相同的圆的方程。
新知应用
解:将已知圆的方程化为标准方程
,
圆心C的坐标为(2,-3),半径为4,故所求圆的半径为
.
所以求圆的方程 .
例2 求过三点O(0,0),M1(1,1),M2(4,2)的圆的方程,并求圆
的半径长和圆心坐标.
新知应用
分析:根据已知条件,很难直接写出圆的标准方程,而圆的一般方程则需确定三个系数,而条件恰好给出三个点坐标,所以用待定系数法求圆的一般方程.
由已知,点O(0,0),M1(1,1),M2(4,2)的坐标满足上述方程,分别代入方程,可得关于D,E,F的三元一次方程组:
所以所求圆的方程为 .
例2 求过三点O(0,0),M1(1,1),M2(4,2)的圆的方程,并指出这个圆的半径和圆心坐标.
解:设所求圆的方程为 .
圆心坐标为(4,-3),圆的半径r = 5 .
用待定系数法求圆方程的大致步骤:
(1)根据题意,选择标准方程或一般方程。
(2)根据条件列出关于a,b,r或D,E,F的方程组;
(3)解出 a,b,r或D,E,F ,代入标准方程或一般方程。
反思感悟
课堂练习
1. 求下列各圆的半径和圆心坐标:
圆的半径为3,圆心坐标为(3,0);
圆的半径为 ,圆心坐标为 .
圆的半径为 ,圆心坐标为 ;
圆的半径为 ,圆心坐标为 ;
课堂练习
2. 已知圆过点A(1,4),B (3,-2),且圆心到直线AB的距离为 .求这个圆的方程.
一、基本知识
1.圆的标准方程.
2.圆的一般方程.
3.求圆的标准方程的方法:
①待定系数法;②代入法(几何法).
(圆心C(a,b),半径r)
,其中
课堂小结
几何方法
求圆心坐标
(两条直线的交点)
(常用弦的中垂线)
求 半径
(圆心到圆上一点距离)
写出圆的标准方程
待定系数法
列关于a,b,r
(或D,E,F)的方程组
解出a,b,r(或D,E,F),
写出标准方程(或一般方程)
二、数学思想
数形结合思想、方程思想、待定系数法、代入法
1、P82 第2题
2、填写本节资料及课时作业
2.2 圆的一般方程
乾县第一中学 陈正东
圆的标准方程
x
y
O
C
M(x,y)
圆心C(a,b),半径r
若圆心为O(0,0),则圆的方程为:
复习引入
圆心 (2, -4) ,半径
(1) 圆 (x-2)2+ (y+4)2=2
(2) 圆 (x+1)2+ (y+2)2=m2
圆心 (-1, -2) ,半径|m|
(m≠0)
分别说出下列圆的圆心与半径:
问题引入:
直线方程有五种不同的形式,它们之间可以相互变通,每一种形式都是关于x,y的一次方程,我们学习了圆的标准方程,它的方程形式具备什么特点呢?还有其他形式吗?
x
y
O
C
M(x,y)
展开得
任何一个圆的方程都是二元二次方程
结论:任何一个圆方程可以写成下面形式:
圆的一般方程
1.圆的标准方程
2.是不是任何一个形如
方程表示的曲线是圆呢?
配方得
不一定是圆
以(1,-2)为圆心,以2为半径的圆
配方得
不是圆
结论:
问题提出
(1)当 时,
表示圆,
(2)当 时,
表示点
(3)当 时,
不表示任何图形
圆心
圆的一般方程
配方,得
圆的一般方程
,其中
圆心
注:圆的一般方程的特点:
(2)没有xy项
(3)D2 +E2 -4F>0
(1)x2 , y2 的系数为1
圆的一般方程
圆的标准方程
获取新知
问题探究二当D=0,E=0或F=0时,圆 的位置分别有什么特点?
C
x
O
y
D=0
E=0
F=0
C
x
y
O
C
x
y
O
圆心
(1) x2+y2-2x+4y-4=0
(2) 2x2+2y2-12x+4y=0
(3) x2+2y2-6x+4y-1=0
(4) x2+y2-12x+6y+50=0
(5) x2+y2-3xy+5x+2y=0
是
圆心(1,-2)半径3
是
圆心(3,-1)半径
不是
不是
不是
练习:判断下列方程能否表示圆的方程,若能,写出圆心与半径.
小试牛刀
例1.求过点M(-1,1),且圆心与已知圆C:
x2+y2-4x+6y-3=0
相同的圆的方程。
新知应用
解:将已知圆的方程化为标准方程
,
圆心C的坐标为(2,-3),半径为4,故所求圆的半径为
.
所以求圆的方程 .
例2 求过三点O(0,0),M1(1,1),M2(4,2)的圆的方程,并求圆
的半径长和圆心坐标.
新知应用
分析:根据已知条件,很难直接写出圆的标准方程,而圆的一般方程则需确定三个系数,而条件恰好给出三个点坐标,所以用待定系数法求圆的一般方程.
由已知,点O(0,0),M1(1,1),M2(4,2)的坐标满足上述方程,分别代入方程,可得关于D,E,F的三元一次方程组:
所以所求圆的方程为 .
例2 求过三点O(0,0),M1(1,1),M2(4,2)的圆的方程,并指出这个圆的半径和圆心坐标.
解:设所求圆的方程为 .
圆心坐标为(4,-3),圆的半径r = 5 .
用待定系数法求圆方程的大致步骤:
(1)根据题意,选择标准方程或一般方程。
(2)根据条件列出关于a,b,r或D,E,F的方程组;
(3)解出 a,b,r或D,E,F ,代入标准方程或一般方程。
反思感悟
课堂练习
1. 求下列各圆的半径和圆心坐标:
圆的半径为3,圆心坐标为(3,0);
圆的半径为 ,圆心坐标为 .
圆的半径为 ,圆心坐标为 ;
圆的半径为 ,圆心坐标为 ;
课堂练习
2. 已知圆过点A(1,4),B (3,-2),且圆心到直线AB的距离为 .求这个圆的方程.
一、基本知识
1.圆的标准方程.
2.圆的一般方程.
3.求圆的标准方程的方法:
①待定系数法;②代入法(几何法).
(圆心C(a,b),半径r)
,其中
课堂小结
几何方法
求圆心坐标
(两条直线的交点)
(常用弦的中垂线)
求 半径
(圆心到圆上一点距离)
写出圆的标准方程
待定系数法
列关于a,b,r
(或D,E,F)的方程组
解出a,b,r(或D,E,F),
写出标准方程(或一般方程)
二、数学思想
数形结合思想、方程思想、待定系数法、代入法
1、P82 第2题
2、填写本节资料及课时作业
