2021-2022学年高一上学期数学北师大版必修2 2.1圆的标准方程 课件(共21张PPT)
文档属性
| 名称 | 2021-2022学年高一上学期数学北师大版必修2 2.1圆的标准方程 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-05 09:59:45 | ||
图片预览






文档简介
(共21张PPT)
北京天坛
创设
情境
广州珠江边的“广州圆大厦”高138米,共33层,总建筑面积约10.5万平方米,外圆直径146.6米,内圆直径47米,是目前全球最大的圆形建筑。
投篮“篮环”
“五环”造型舞蹈
2.1圆的标准方程
乾县第一中学 陈正东
M
O
x
y
C(a,b)
r
温故知新
平面内与定点距离等于定长的点的集合叫作圆,定点称为圆心,定长称为半径.
问题一:什么是圆?初中时我们是如何给圆下定义的?
定点就是圆心 定长就是半径.
问题二:确定一个圆需要哪几个要素?
圆心:
半径:
确定圆的位置
确定圆的大小
1.回顾在平面直角坐标系中,坐标法求直线的
步骤,如何用坐标法来刻画圆呢?
坐标法求直线的步骤:
1、建系;
2、设点;
3、列式;
4、化简;
5、检验。
2. 学习了两点之间的距离公式:设
则
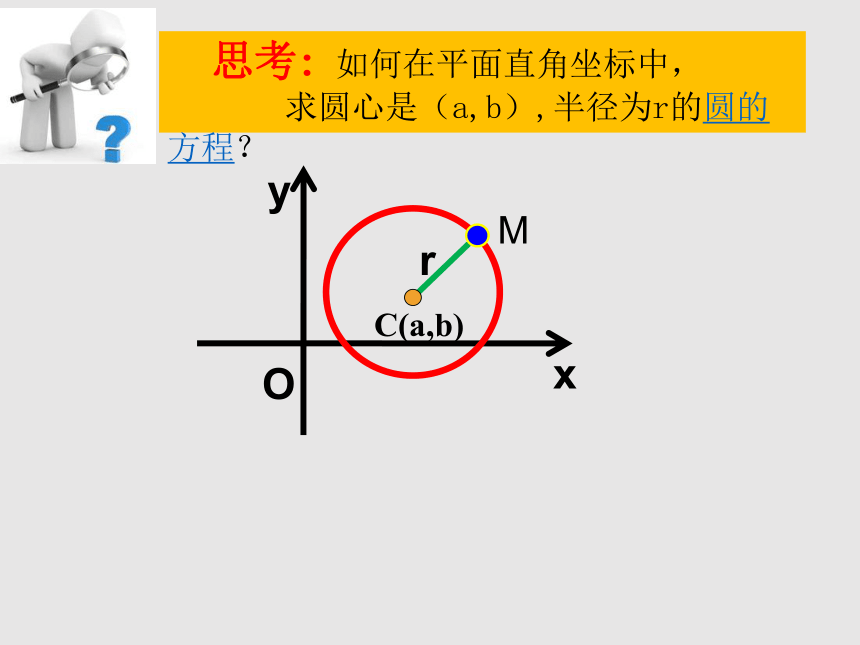
思考:如何在平面直角坐标中,
求圆心是(a,b),半径为r的圆的方程?
M
O
x
y
C(a,b)
r
M(x,y)
O
x
y
C(a,b)
r
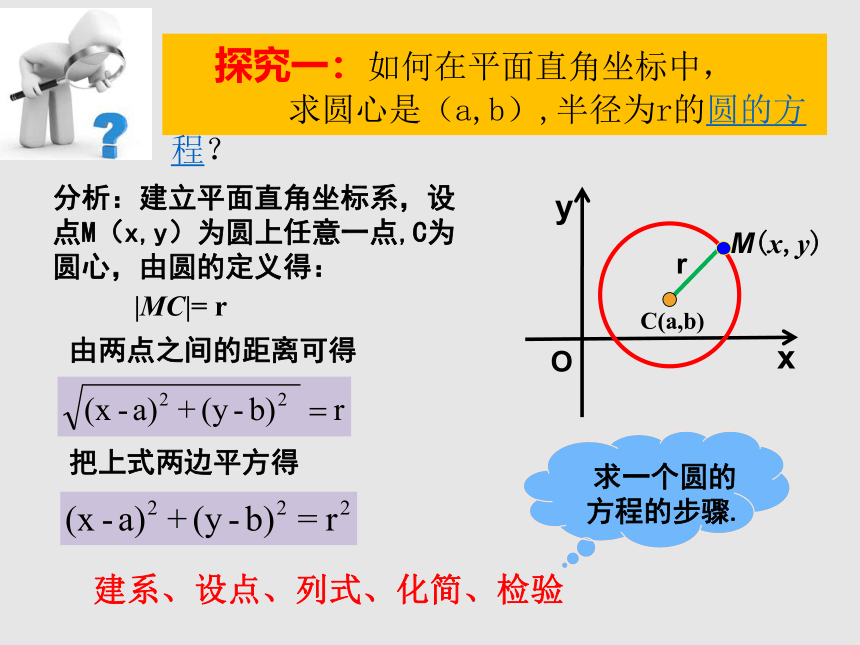
探究一:如何在平面直角坐标中,
求圆心是(a,b),半径为r的圆的方程?
分析:建立平面直角坐标系,设点M(x,y)为圆上任意一点,C为圆心,由圆的定义得:
建系、设点、列式、化简、检验
|MC|= r
由两点之间的距离可得
把上式两边平方得
求一个圆的方程的步骤.
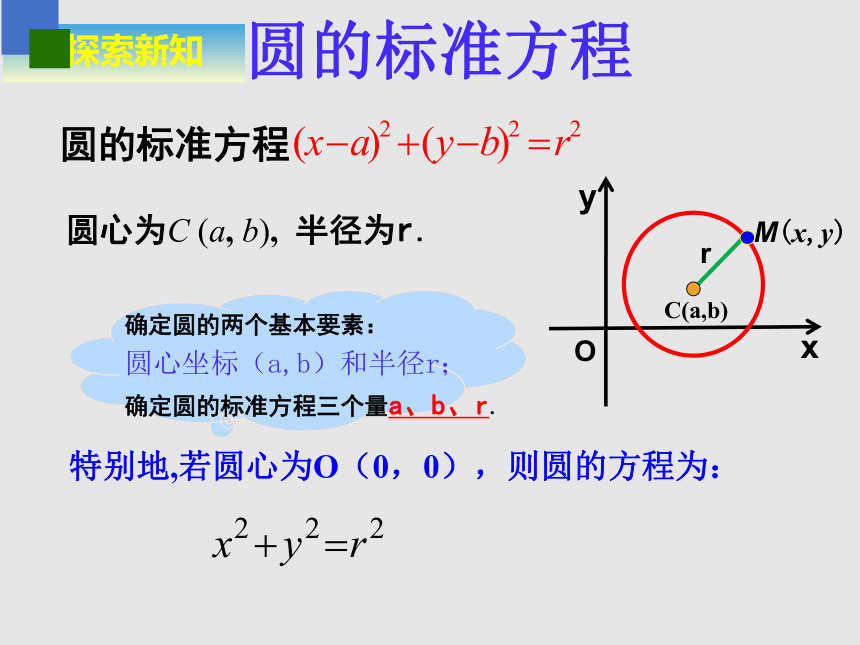
特别地,若圆心为O(0,0),则圆的方程为:
圆的标准方程
M(x,y)
O
x
y
C(a,b)
r
确定圆的两个基本要素:
圆心坐标(a,b)和半径r;
确定圆的标准方程三个量a、b、r.
探索新知
圆的标准方程
圆心为C (a, b), 半径为r.
1.圆心为 A(2, –1),半径长等于5的圆的方程为( )
A.(x – 2 )2+(y – 1 )2=25 B.(x – 2 )2+(y + 1 )2=25
C.(x – 2 )2+(y + 1 )2=5 D.(x + 2 )2+(y – 1 )2=5
2.圆(x-2)2+y2 =4的圆心C的坐标及半径r分别为( )
A. C(2,0) r = 4 B. C(–2,0) r = 2
C. C(0,2) r = 2 D. C(2,0) r = 2
变式:圆(x+1)2+(y– )2=a2,(a 0)的圆心,半径r是?
变式:圆心在C(8,–3),且经过点M(5,1)的圆的方程
小试
牛刀
写出圆心为 ,半径长等于5的圆的方程,并判断点 , 是否在这个圆上。
把 的坐标代入方程 左右两边相等,点 的坐标适合圆的方程,所以点
在这个圆上;
把点 的坐标代入此方程,左右两边不相等,点 的坐标不适合圆的方程,所以点 不在这个圆上.
探究二:点与圆的位置关系
解:圆心是 ,半径长等于5的圆的标准方程 是:
|OM||OM|>r
点在圆外
探究二:点与圆的位置关系
在平面几何中,如何确定点与圆的位置关系?
|OM|=r
点在圆上
M
O
O
M
M
O
点在圆内
|OM|M
O
O
M
M
O
(x0-a)2+(y0-b)2 < r2时,点M在圆C内;
(x0-a)2+(y0-b)2 = r2时,点M在圆C上;
(x0-a)2+(y0-b)2 > r2时,点M在圆C外.
点与圆的位置关系
M
O
O
M
M
O
点P( ,5)与圆x2+y2=25的位置关系
( )
A.在圆外 B.在圆上
C.在圆内 D.在圆上或圆外
A
随堂小练习
m
1
D
例1.求适合下列条件的圆的标准方程:
例题应用
(1)圆心在点C(-2,1),经过点A(2,-2);
x
y
o
.C(-2,1)
.A(2,-2)
解:由题意得,r=
所以,圆的方程为:
(x+2)2+(y-1)2=25
(2)以M(4,9),N(6,3)为直径.
x
y
o
.M(4,9)
.N(6,3)
.C
例1.求适合下列条件的圆的标准方程:
解:根据题意得,圆心C(a,b)是MN的中点,则 a=5, b=6,
根据两点间距离公式,得圆的半径
所以,所求圆的方程为(x-5)2+(y-6)2=10
例2.求以C(1,3)为圆心,并且和直线3x-4y-7=0 相切的圆的方程。
C
y
x
O
解:因为圆C和直线3x-4y-7=0相切
所以圆心C到这条直线的距离等于半径r
根据点到直线的距离公式,得
| 3×1— 4×3 — 7 |
32+(-4)2
=
5
16
r =
因此,所求圆的方程是 (x-1)2+(y-3)2
=
25
256
例3. △ABC的三个顶点的坐标分别A(5,1), B(7,-3),C(2, -8),求它的外接圆的方程.
解:设所求圆的方程是 (1)
因为A(5,1), B(7,-3),C(2, -8) 都在圆上,所以它们的坐标都满足方程(1).于是
待定系数法
所求圆的方程为
例3.△ABC的三个顶点的坐标分别A(5,1), B(7,-3),C(2, -8),求它的外接圆的方程.
B(7,-3)
C(2,-8)
A(5,1)
O
y
x
L2
L1
D
R
几何法
规律归纳:
求圆的标准方程一般有两种思路:
(1) 待定系数法,这种方法体现了方程的思想,思路直接,是通用方法;
(2) 几何法,由圆的几何性质直接求出圆心坐标和半径,然后代入标准方程。
由圆的几何性质易得圆心坐标和半径时,用几何法可以简化运算,其他情况可用待定系数法。
课堂小结
圆心C(a,b),半径r
(1)牢记 圆的标准方程
(2)明确 三个条件 确定一个圆
(3)体会 ①待定系数法
②数形结合法
布置作业
P81 第 1 题
练习:
填写本节资料及课时作业
Goodbye!
谢谢!
北京天坛
创设
情境
广州珠江边的“广州圆大厦”高138米,共33层,总建筑面积约10.5万平方米,外圆直径146.6米,内圆直径47米,是目前全球最大的圆形建筑。
投篮“篮环”
“五环”造型舞蹈
2.1圆的标准方程
乾县第一中学 陈正东
M
O
x
y
C(a,b)
r
温故知新
平面内与定点距离等于定长的点的集合叫作圆,定点称为圆心,定长称为半径.
问题一:什么是圆?初中时我们是如何给圆下定义的?
定点就是圆心 定长就是半径.
问题二:确定一个圆需要哪几个要素?
圆心:
半径:
确定圆的位置
确定圆的大小
1.回顾在平面直角坐标系中,坐标法求直线的
步骤,如何用坐标法来刻画圆呢?
坐标法求直线的步骤:
1、建系;
2、设点;
3、列式;
4、化简;
5、检验。
2. 学习了两点之间的距离公式:设
则
思考:如何在平面直角坐标中,
求圆心是(a,b),半径为r的圆的方程?
M
O
x
y
C(a,b)
r
M(x,y)
O
x
y
C(a,b)
r
探究一:如何在平面直角坐标中,
求圆心是(a,b),半径为r的圆的方程?
分析:建立平面直角坐标系,设点M(x,y)为圆上任意一点,C为圆心,由圆的定义得:
建系、设点、列式、化简、检验
|MC|= r
由两点之间的距离可得
把上式两边平方得
求一个圆的方程的步骤.
特别地,若圆心为O(0,0),则圆的方程为:
圆的标准方程
M(x,y)
O
x
y
C(a,b)
r
确定圆的两个基本要素:
圆心坐标(a,b)和半径r;
确定圆的标准方程三个量a、b、r.
探索新知
圆的标准方程
圆心为C (a, b), 半径为r.
1.圆心为 A(2, –1),半径长等于5的圆的方程为( )
A.(x – 2 )2+(y – 1 )2=25 B.(x – 2 )2+(y + 1 )2=25
C.(x – 2 )2+(y + 1 )2=5 D.(x + 2 )2+(y – 1 )2=5
2.圆(x-2)2+y2 =4的圆心C的坐标及半径r分别为( )
A. C(2,0) r = 4 B. C(–2,0) r = 2
C. C(0,2) r = 2 D. C(2,0) r = 2
变式:圆(x+1)2+(y– )2=a2,(a 0)的圆心,半径r是?
变式:圆心在C(8,–3),且经过点M(5,1)的圆的方程
小试
牛刀
写出圆心为 ,半径长等于5的圆的方程,并判断点 , 是否在这个圆上。
把 的坐标代入方程 左右两边相等,点 的坐标适合圆的方程,所以点
在这个圆上;
把点 的坐标代入此方程,左右两边不相等,点 的坐标不适合圆的方程,所以点 不在这个圆上.
探究二:点与圆的位置关系
解:圆心是 ,半径长等于5的圆的标准方程 是:
|OM|
点在圆外
探究二:点与圆的位置关系
在平面几何中,如何确定点与圆的位置关系?
|OM|=r
点在圆上
M
O
O
M
M
O
点在圆内
|OM|
O
O
M
M
O
(x0-a)2+(y0-b)2 < r2时,点M在圆C内;
(x0-a)2+(y0-b)2 = r2时,点M在圆C上;
(x0-a)2+(y0-b)2 > r2时,点M在圆C外.
点与圆的位置关系
M
O
O
M
M
O
点P( ,5)与圆x2+y2=25的位置关系
( )
A.在圆外 B.在圆上
C.在圆内 D.在圆上或圆外
A
随堂小练习
m
1
D
例1.求适合下列条件的圆的标准方程:
例题应用
(1)圆心在点C(-2,1),经过点A(2,-2);
x
y
o
.C(-2,1)
.A(2,-2)
解:由题意得,r=
所以,圆的方程为:
(x+2)2+(y-1)2=25
(2)以M(4,9),N(6,3)为直径.
x
y
o
.M(4,9)
.N(6,3)
.C
例1.求适合下列条件的圆的标准方程:
解:根据题意得,圆心C(a,b)是MN的中点,则 a=5, b=6,
根据两点间距离公式,得圆的半径
所以,所求圆的方程为(x-5)2+(y-6)2=10
例2.求以C(1,3)为圆心,并且和直线3x-4y-7=0 相切的圆的方程。
C
y
x
O
解:因为圆C和直线3x-4y-7=0相切
所以圆心C到这条直线的距离等于半径r
根据点到直线的距离公式,得
| 3×1— 4×3 — 7 |
32+(-4)2
=
5
16
r =
因此,所求圆的方程是 (x-1)2+(y-3)2
=
25
256
例3. △ABC的三个顶点的坐标分别A(5,1), B(7,-3),C(2, -8),求它的外接圆的方程.
解:设所求圆的方程是 (1)
因为A(5,1), B(7,-3),C(2, -8) 都在圆上,所以它们的坐标都满足方程(1).于是
待定系数法
所求圆的方程为
例3.△ABC的三个顶点的坐标分别A(5,1), B(7,-3),C(2, -8),求它的外接圆的方程.
B(7,-3)
C(2,-8)
A(5,1)
O
y
x
L2
L1
D
R
几何法
规律归纳:
求圆的标准方程一般有两种思路:
(1) 待定系数法,这种方法体现了方程的思想,思路直接,是通用方法;
(2) 几何法,由圆的几何性质直接求出圆心坐标和半径,然后代入标准方程。
由圆的几何性质易得圆心坐标和半径时,用几何法可以简化运算,其他情况可用待定系数法。
课堂小结
圆心C(a,b),半径r
(1)牢记 圆的标准方程
(2)明确 三个条件 确定一个圆
(3)体会 ①待定系数法
②数形结合法
布置作业
P81 第 1 题
练习:
填写本节资料及课时作业
Goodbye!
谢谢!
