沪科版数学九年级上册 相似三角形证明经典类型 教案
文档属性
| 名称 | 沪科版数学九年级上册 相似三角形证明经典类型 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 133.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-05 15:18:54 | ||
图片预览

文档简介
三角形相似的几种常见判定类型
教学目标:
知识与技能:理解并掌握相似三角形的判定方法。
数学思考:以问题的形式,和学生一起动手和探究相似的几种形式,并作归纳。
解决问题:学生动手和探究归纳达到掌握相似三角形判定的方法的目的.
情感态度:培养学生积极的思考、动手、观察的能力,使学生感悟几何知识在生活中的价值.
教学重点:
在学完相似三角形基础上,进一步研究相似三角形的本质,以完成对相似三角形的定义,判定全面研究。相似三角形的判定还是相似三角形性质的基础,是以后研究圆中线段关系的工具。掌握相似三角形的判定方法,总结出几种类型图形
教学难点:
它的难度较大,因为前面所学的知识主要是证明两条线段的相等,两个角相等。两条直线平行、垂直等。借助于图形进行观察比较困难,主要是借助逻辑的体系进行分析、探索,难度较大。理解和应用相似三角形判定,掌握几种特定的模型,有利于以后解决复杂的综合题。
教学过程:
对于几何题,只要条件稍加变化,或者图形稍作改动,就会成为一个新的题目,但若能抓住要点,进行归纳分类,就能抓准其中解答的关键,从而理清思路,简化证明的步骤.
相似三角形常见基本类型有:平行型、斜交型、垂直型、旋转型和“M”型五类.针对不同类型,在解答时应掌握以下几种常见思路:
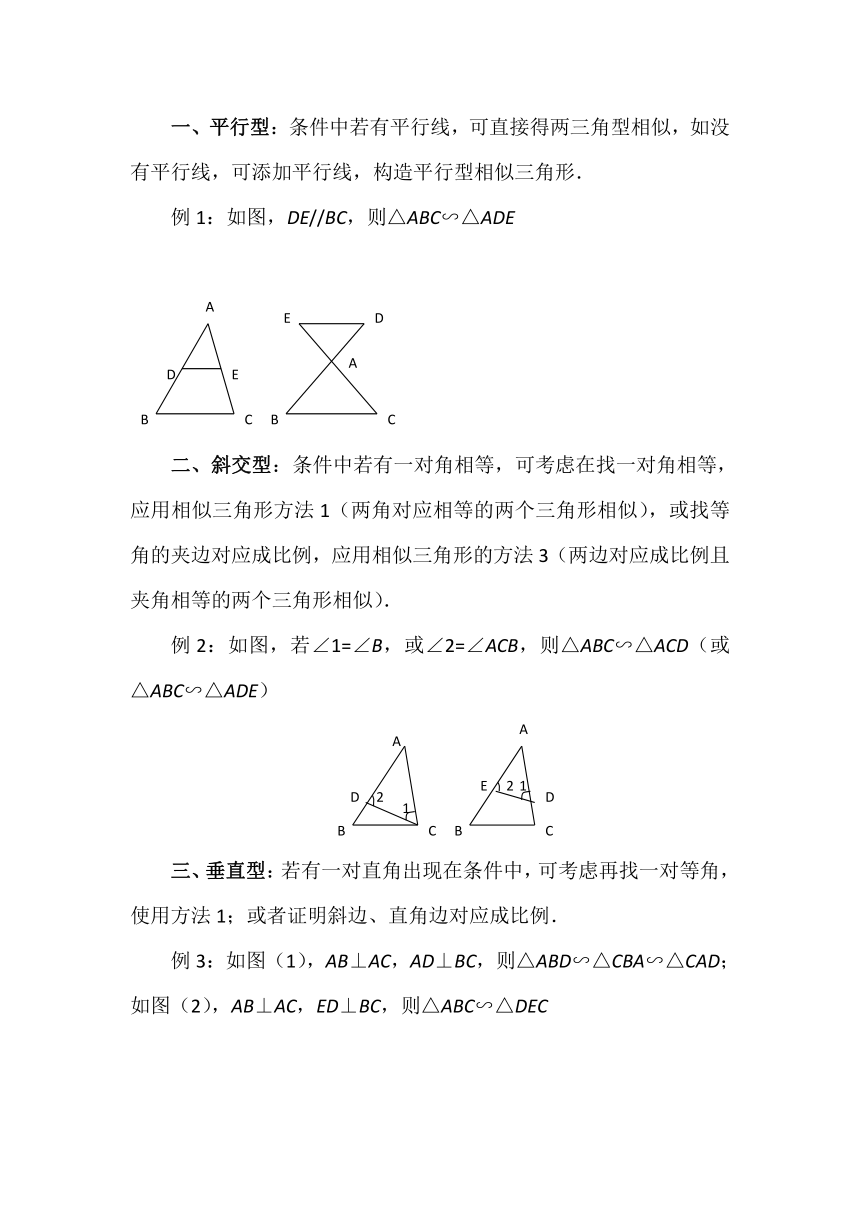
一、平行型:条件中若有平行线,可直接得两三角型相似,如没有平行线,可添加平行线,构造平行型相似三角形.
例1:如图,DE//BC,则△ABC∽△ADE
二、斜交型:条件中若有一对角相等,可考虑在找一对角相等,应用相似三角形方法1(两角对应相等的两个三角形相似),或找等角的夹边对应成比例,应用相似三角形的方法3(两边对应成比例且夹角相等的两个三角形相似).
例2:如图,若∠1=∠B,或∠2=∠ACB,则△ABC∽△ACD(或△ABC∽△ADE)
三、垂直型:若有一对直角出现在条件中,可考虑再找一对等角,使用方法1;或者证明斜边、直角边对应成比例.
例3:如图(1),AB⊥AC,AD⊥BC,则△ABD∽△CBA∽△CAD;如图(2),AB⊥AC,ED⊥BC,则△ABC∽△DEC
四、旋转型:条件中若有两边对应成比例,可寻找夹角相等,应用相似三角形的方法3,常见于旋转型题目中;或设法证明第三对边与其他两边对应成比例,应用相似三角形方法2(三边对应成比例的两个三角形相似).
例4:如图,∠1=∠2,∠3=∠4,则△ABD∽△ACE.
五、“M”型:若有三个角相等出现在如图的条件中,我们可以考虑,两个三角形相似,从而求线段的长。
如图1,∠B=∠C=∠AED, 则△ABE∽△ECD.
如图2,∠B=∠C=∠AED=α,则△ABE∽△ECD.
例: 已知:D为BC上一点, ∠B= ∠C= ∠EDF=60°,BE=6,CD=3,CF=4,
则AF=_______
对于上述基本图形,在不同题目中尽管可采用不同方法,但其中的思考方式是完全一致的.
A
B
D
E
C
A
B
C
D
E
A
B
C
D
1
2
A
B
C
D
1
2
E
A
B
C
D
(1)
A
B
C
D
(2)
E
A
B
C
D
E
1
2
3
4
D
A
C
B
E
D
B
C
E
α
α
α
A
A
F
E
D
C
B
教学目标:
知识与技能:理解并掌握相似三角形的判定方法。
数学思考:以问题的形式,和学生一起动手和探究相似的几种形式,并作归纳。
解决问题:学生动手和探究归纳达到掌握相似三角形判定的方法的目的.
情感态度:培养学生积极的思考、动手、观察的能力,使学生感悟几何知识在生活中的价值.
教学重点:
在学完相似三角形基础上,进一步研究相似三角形的本质,以完成对相似三角形的定义,判定全面研究。相似三角形的判定还是相似三角形性质的基础,是以后研究圆中线段关系的工具。掌握相似三角形的判定方法,总结出几种类型图形
教学难点:
它的难度较大,因为前面所学的知识主要是证明两条线段的相等,两个角相等。两条直线平行、垂直等。借助于图形进行观察比较困难,主要是借助逻辑的体系进行分析、探索,难度较大。理解和应用相似三角形判定,掌握几种特定的模型,有利于以后解决复杂的综合题。
教学过程:
对于几何题,只要条件稍加变化,或者图形稍作改动,就会成为一个新的题目,但若能抓住要点,进行归纳分类,就能抓准其中解答的关键,从而理清思路,简化证明的步骤.
相似三角形常见基本类型有:平行型、斜交型、垂直型、旋转型和“M”型五类.针对不同类型,在解答时应掌握以下几种常见思路:
一、平行型:条件中若有平行线,可直接得两三角型相似,如没有平行线,可添加平行线,构造平行型相似三角形.
例1:如图,DE//BC,则△ABC∽△ADE
二、斜交型:条件中若有一对角相等,可考虑在找一对角相等,应用相似三角形方法1(两角对应相等的两个三角形相似),或找等角的夹边对应成比例,应用相似三角形的方法3(两边对应成比例且夹角相等的两个三角形相似).
例2:如图,若∠1=∠B,或∠2=∠ACB,则△ABC∽△ACD(或△ABC∽△ADE)
三、垂直型:若有一对直角出现在条件中,可考虑再找一对等角,使用方法1;或者证明斜边、直角边对应成比例.
例3:如图(1),AB⊥AC,AD⊥BC,则△ABD∽△CBA∽△CAD;如图(2),AB⊥AC,ED⊥BC,则△ABC∽△DEC
四、旋转型:条件中若有两边对应成比例,可寻找夹角相等,应用相似三角形的方法3,常见于旋转型题目中;或设法证明第三对边与其他两边对应成比例,应用相似三角形方法2(三边对应成比例的两个三角形相似).
例4:如图,∠1=∠2,∠3=∠4,则△ABD∽△ACE.
五、“M”型:若有三个角相等出现在如图的条件中,我们可以考虑,两个三角形相似,从而求线段的长。
如图1,∠B=∠C=∠AED, 则△ABE∽△ECD.
如图2,∠B=∠C=∠AED=α,则△ABE∽△ECD.
例: 已知:D为BC上一点, ∠B= ∠C= ∠EDF=60°,BE=6,CD=3,CF=4,
则AF=_______
对于上述基本图形,在不同题目中尽管可采用不同方法,但其中的思考方式是完全一致的.
A
B
D
E
C
A
B
C
D
E
A
B
C
D
1
2
A
B
C
D
1
2
E
A
B
C
D
(1)
A
B
C
D
(2)
E
A
B
C
D
E
1
2
3
4
D
A
C
B
E
D
B
C
E
α
α
α
A
A
F
E
D
C
B
