沪科版数学九年级上册 21.1 二次函数课件(共18张PPT)
文档属性
| 名称 | 沪科版数学九年级上册 21.1 二次函数课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 182.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-05 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
21.1 二次函数
1. 函数的定义:
(在某个变化过程中,有两个变量x和y,对于x在某一范围内的每一个确定的值,变量y都有一个唯一确定的值与它对应,那么我们称y是x的函数,其中x是自变量,y是x的函数.)
2. 大家还记得我们学过哪些函数吗
( 正比例函数,一次函数)
打开你的记忆
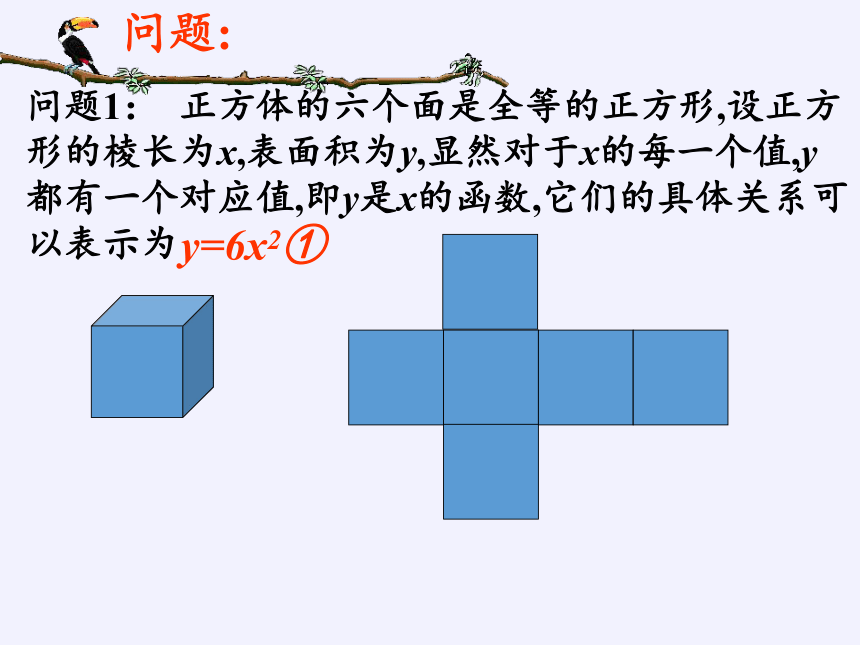
问题1: 正方体的六个面是全等的正方形,设正方形的棱长为x,表面积为y,显然对于x的每一个值,y都有一个对应值,即y是x的函数,它们的具体关系可以表示为
问题:
y=6x2①
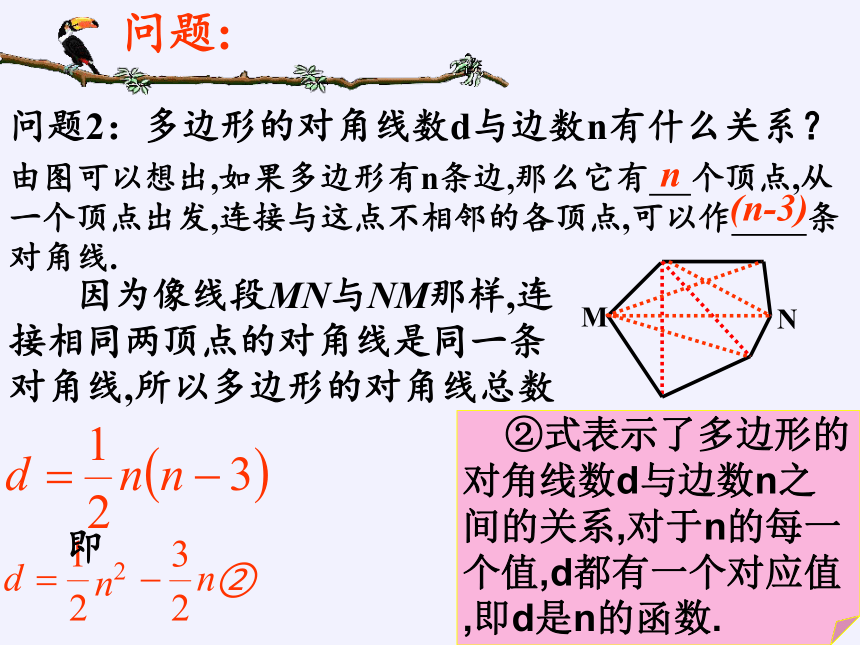
问题2:多边形的对角线数d与边数n有什么关系?
问题:
由图可以想出,如果多边形有n条边,那么它有 个顶点,从一个顶点出发,连接与这点不相邻的各顶点,可以作 条对角线.
n
(n-3)
因为像线段MN与NM那样,连接相同两顶点的对角线是同一条对角线,所以多边形的对角线总数
M
N
即
②式表示了多边形的对角线数d与边数n之间的关系,对于n的每一个值,d都有一个对应值,即d是n的函数.
问题3: 某工厂一种产品今年的年产量是20件,计划明后两年增加产量.如果每年的增长率为x,那么两年后这种产品的产量y将随计划所定的x的值而确定,y与x之间的关系应怎样表示?
问题:
这种产品的原产量是20件, 一年后的产量是
件,再经过一年后的产量是 件,即两年后的产量为
20(1+x)
20(1+x)2
即
③式表示了两年后的产量y与增长率x之间的关系,对于x的每一个值, y都有一个对应值,即y是x的函数.
y是x的函数吗 y是x的一次函数?
2、定义:一般地,形如y=ax +bx+c(a,b,c是常数,a≠ 0)的函数叫做二次函数。
观察与总结
y=6x2①
我们把形如y=ax +bx+c(其中a,b,c是常数,a≠0)的函数叫做二次函数
知识归纳
为什么a ≠0呢
称:a为二次项系数,
ax2叫做二次项
b为一次项系数,
bx叫做一次项
c为常数项,
2、定义:一般地,形如y=ax +bx+c(a,b,c是常数,a≠ 0)的函数叫做x的二次函数。
(1)等号左边是变量y,右边是关于自变量x的
(3 )等式的右边最高次数为 ,可以没有一次项和常数项,但不能没有二次项。
注意:
(2)a,b,c为常数,且
(4)x的取值范围是 。
整式
a≠0.
2
任意实数
二次函数的一般形式:
y=ax2+bx+c (其中a、b、c是常数,a≠0)
二次函数的特殊形式:
当b=0时, y=ax2+c
当c=0时, y=ax2+bx
当b=0,c=0时, y=ax2
观察与总结
函数解析式 二次项系数a 一次项系数b 常数项 c
0
0
2
4
2
-1
58
-112
13
0
说出下列二次函数的二次项系数、一次项系数和常数项:
试一试:
二次函数y=ax +bx+c中a≠0,而b、c可以为0.
例1、下列函数中,哪些是二次函数?若是,分别指出二次项系数,一次项系数,常数项.
(1) y=3(x-1) +1
(2)y=x+
(3)s=3-2t
(4)y=(x+3) -x
(5)y= -x
(6)v= r
1
x
__
例题与练习
(7) y=x +x +25
(8)y=2 +2x
(是)
(否)
(是)
(否)
(否)
(是)
(否)
(否)
例题与练习
例2. y=(m+3)x (1) m取什么值时,此函数是正比例函数 (2) m取什么值时,此函数是二次函数
m2-7
看谁算得快!
1.函数 是一次函数,求k的值。
0
2.函数 是二次函数,
求m的值。
2
3.函数 是二次函数,
求m的值
2
1、下列函数中,(x是自变量),是二次函数的为( )
A y=ax2+bx+c B y2=x2-4x+1
C y=x2 D y=2+ √x2 +1
随堂练习
2.函数 y=(m-n)x2+ mx+n 是二次函数的条件是( )
A m,n是常数,且m≠0
B m,n是常数,且n≠0
C m,n是常数,且m≠n
D m,n为任何实数
3、圆的半径是1cm,假设半径增加xcm
时,圆的面积增加ycm 。
(1)写出y与x之间的函数关系表达式;
(2)当圆的半径分别增加1cm,2cm时,
圆的面积增加多少?
随堂练习
回味无穷
小结 拓展
1.定义:一般地,形如y=ax +bx+c(a,b,c是常数,a≠0)的函数叫做x的二次函数.其中,是x自变量,a,b,c分别是函数表达式的二次项系数、一次项系数和常数项.
y=ax +bx+c(a,b,c是常数,a≠0)的几种不同表示形式:
(1)y=ax (a≠0,b=0,c=0,).
(2)y=ax +c(a≠0,b=0,c≠0).
(3)y=ax +bx(a≠0,b≠0,c=0).
2.定义的实质是:ax +bx+c是整式,自变量x的最高次数是二次,自变量x的取值范围是全体实数.
作业:
习题21.1
第1,2题
谢 谢
21.1 二次函数
1. 函数的定义:
(在某个变化过程中,有两个变量x和y,对于x在某一范围内的每一个确定的值,变量y都有一个唯一确定的值与它对应,那么我们称y是x的函数,其中x是自变量,y是x的函数.)
2. 大家还记得我们学过哪些函数吗
( 正比例函数,一次函数)
打开你的记忆
问题1: 正方体的六个面是全等的正方形,设正方形的棱长为x,表面积为y,显然对于x的每一个值,y都有一个对应值,即y是x的函数,它们的具体关系可以表示为
问题:
y=6x2①
问题2:多边形的对角线数d与边数n有什么关系?
问题:
由图可以想出,如果多边形有n条边,那么它有 个顶点,从一个顶点出发,连接与这点不相邻的各顶点,可以作 条对角线.
n
(n-3)
因为像线段MN与NM那样,连接相同两顶点的对角线是同一条对角线,所以多边形的对角线总数
M
N
即
②式表示了多边形的对角线数d与边数n之间的关系,对于n的每一个值,d都有一个对应值,即d是n的函数.
问题3: 某工厂一种产品今年的年产量是20件,计划明后两年增加产量.如果每年的增长率为x,那么两年后这种产品的产量y将随计划所定的x的值而确定,y与x之间的关系应怎样表示?
问题:
这种产品的原产量是20件, 一年后的产量是
件,再经过一年后的产量是 件,即两年后的产量为
20(1+x)
20(1+x)2
即
③式表示了两年后的产量y与增长率x之间的关系,对于x的每一个值, y都有一个对应值,即y是x的函数.
y是x的函数吗 y是x的一次函数?
2、定义:一般地,形如y=ax +bx+c(a,b,c是常数,a≠ 0)的函数叫做二次函数。
观察与总结
y=6x2①
我们把形如y=ax +bx+c(其中a,b,c是常数,a≠0)的函数叫做二次函数
知识归纳
为什么a ≠0呢
称:a为二次项系数,
ax2叫做二次项
b为一次项系数,
bx叫做一次项
c为常数项,
2、定义:一般地,形如y=ax +bx+c(a,b,c是常数,a≠ 0)的函数叫做x的二次函数。
(1)等号左边是变量y,右边是关于自变量x的
(3 )等式的右边最高次数为 ,可以没有一次项和常数项,但不能没有二次项。
注意:
(2)a,b,c为常数,且
(4)x的取值范围是 。
整式
a≠0.
2
任意实数
二次函数的一般形式:
y=ax2+bx+c (其中a、b、c是常数,a≠0)
二次函数的特殊形式:
当b=0时, y=ax2+c
当c=0时, y=ax2+bx
当b=0,c=0时, y=ax2
观察与总结
函数解析式 二次项系数a 一次项系数b 常数项 c
0
0
2
4
2
-1
58
-112
13
0
说出下列二次函数的二次项系数、一次项系数和常数项:
试一试:
二次函数y=ax +bx+c中a≠0,而b、c可以为0.
例1、下列函数中,哪些是二次函数?若是,分别指出二次项系数,一次项系数,常数项.
(1) y=3(x-1) +1
(2)y=x+
(3)s=3-2t
(4)y=(x+3) -x
(5)y= -x
(6)v= r
1
x
__
例题与练习
(7) y=x +x +25
(8)y=2 +2x
(是)
(否)
(是)
(否)
(否)
(是)
(否)
(否)
例题与练习
例2. y=(m+3)x (1) m取什么值时,此函数是正比例函数 (2) m取什么值时,此函数是二次函数
m2-7
看谁算得快!
1.函数 是一次函数,求k的值。
0
2.函数 是二次函数,
求m的值。
2
3.函数 是二次函数,
求m的值
2
1、下列函数中,(x是自变量),是二次函数的为( )
A y=ax2+bx+c B y2=x2-4x+1
C y=x2 D y=2+ √x2 +1
随堂练习
2.函数 y=(m-n)x2+ mx+n 是二次函数的条件是( )
A m,n是常数,且m≠0
B m,n是常数,且n≠0
C m,n是常数,且m≠n
D m,n为任何实数
3、圆的半径是1cm,假设半径增加xcm
时,圆的面积增加ycm 。
(1)写出y与x之间的函数关系表达式;
(2)当圆的半径分别增加1cm,2cm时,
圆的面积增加多少?
随堂练习
回味无穷
小结 拓展
1.定义:一般地,形如y=ax +bx+c(a,b,c是常数,a≠0)的函数叫做x的二次函数.其中,是x自变量,a,b,c分别是函数表达式的二次项系数、一次项系数和常数项.
y=ax +bx+c(a,b,c是常数,a≠0)的几种不同表示形式:
(1)y=ax (a≠0,b=0,c=0,).
(2)y=ax +c(a≠0,b=0,c≠0).
(3)y=ax +bx(a≠0,b≠0,c=0).
2.定义的实质是:ax +bx+c是整式,自变量x的最高次数是二次,自变量x的取值范围是全体实数.
作业:
习题21.1
第1,2题
谢 谢
