沪科版数学九年级上册 22.3 相似三角形的性质(课件)(共18张PPT)
文档属性
| 名称 | 沪科版数学九年级上册 22.3 相似三角形的性质(课件)(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 194.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-05 15:56:25 | ||
图片预览



文档简介
(共18张PPT)
22.3 相似三角形的性质
(1)什么叫相似三角形?什么是他们的相似比?
对应角相等、对应边成比例的三角形,叫做
相似三角形.
相似多边形对应边长度的比叫相似比
(2)如何判定两个三角形相似?
①两个角对应相等;
②两边对应成比例,且夹角相等;
③三边对应成比例.
回顾与复习
A
B
C
A/
B/
C/
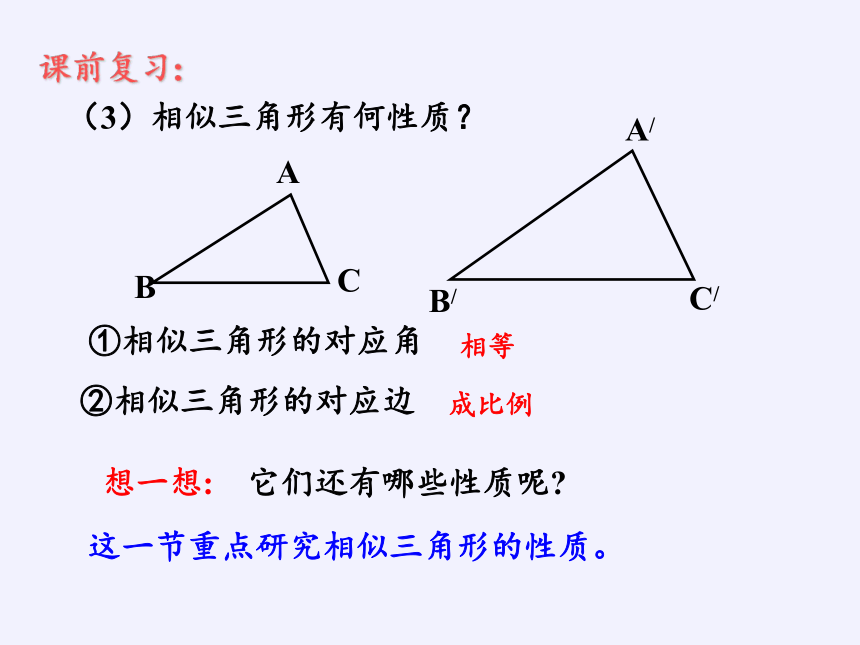
①相似三角形的对应角
②相似三角形的对应边
想一想: 它们还有哪些性质呢
课前复习:
(3)相似三角形有何性质?
这一节重点研究相似三角形的性质。
相等
成比例
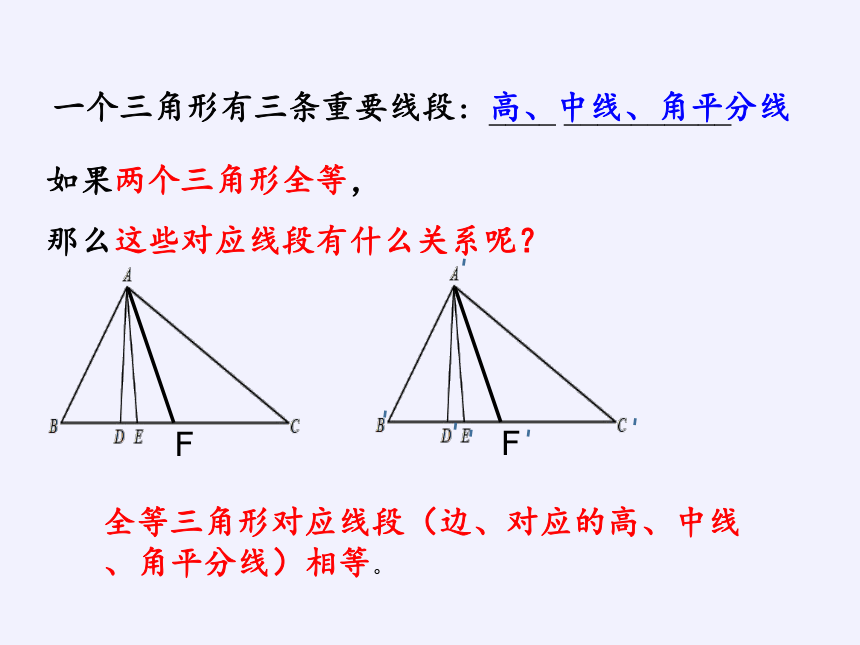
一个三角形有三条重要线段:____ __________
如果两个三角形全等,
那么这些对应线段有什么关系呢?
高、中线、角平分线
F
F
全等三角形对应线段(边、对应的高、中线、角平分线)相等。
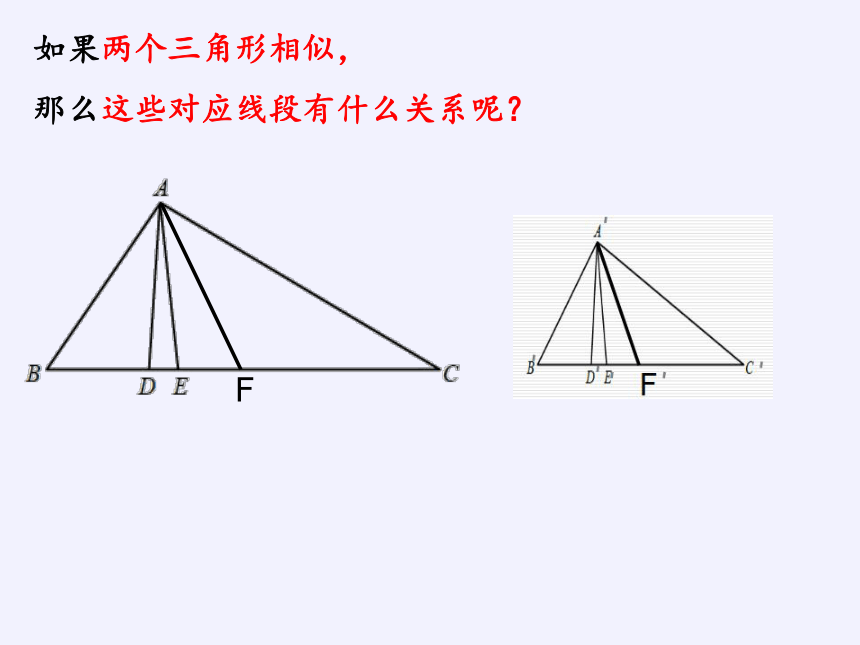
如果两个三角形相似,
那么这些对应线段有什么关系呢?
F
在生活中,我们经常利用相似的知识解决建筑类问题.如图,小王依据图纸上的△ABC,以1:2的比例建造了模型房梁△A’B’C’,CD和C’D’分别是它们的立柱。
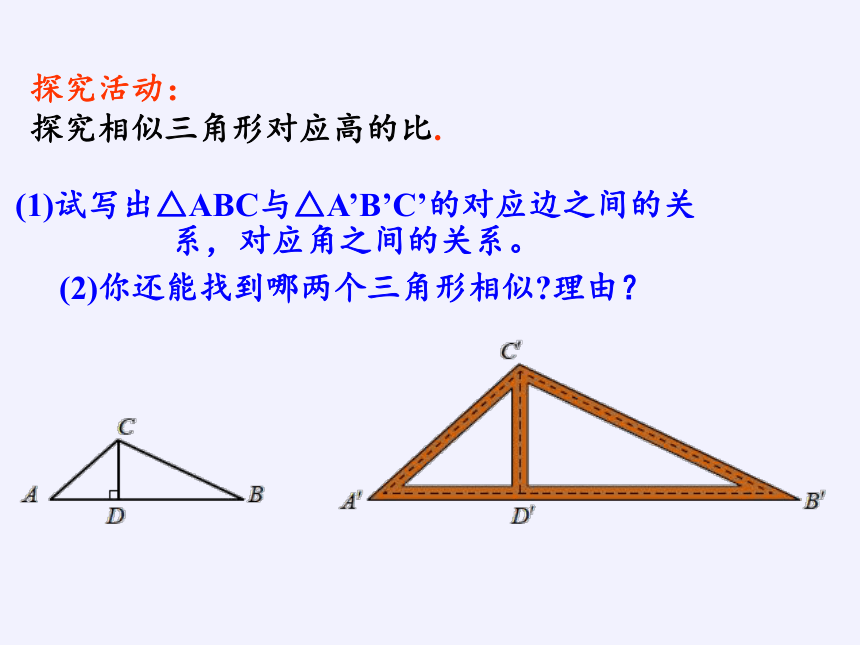
探究活动:
探究相似三角形对应高的比.
(1)试写出△ABC与△A’B’C’的对应边之间的关系,对应角之间的关系。
(2)你还能找到哪两个三角形相似 理由?
探究活动:
探究相似三角形对应高的比.
(3)如果CD=1.5cm,那么模型房的房梁立柱有多高?
(4)据此,你可以发现相似三角形怎样的性质?
探究活动:
探究相似三角形对应高的比.
猜想:相似三角形对应高的比等于相似比.
D'
C'
B'
A'
D
C
B
A
∽
推理及猜想:
结论:相似三角形对应高的比等于相似比.
类似结论
自主思考---
结论:相似三角形对应角的角平分线的比等于相似比.
类似结论
D'
C'
B'
A'
D
C
B
A
∽
自主思考---
结论:相似三角形对应中线的比等于相似比.
对应高的比
对应中线的比
对应角平分线的比
相
似
三
角
形
都等于相似比.
相似三角形的性质
定理 相似三角形对应高的比、对应角平分线的比、对应中线的比都等于相似比.
1.若两个相似三角形对应高的比为1:3,则这两个三角形的相似比是______
小试牛刀
1:3
2.△ABC∽△A’B’C’,AD和A’D’是
它们的对应角平分线,已知AD=4cm,
A’D’=10cm,那么对应高的比
是________
2:5
3、已知△ABC∽△DEF,BG、EH分△ABC和 △DEF的角平分线,BC=6cm,EF=4cm,BG=4.8cm.求EH的长.
小试牛刀
B
A
C
G
D
E
F
H
4.如图是一个照相机成像的示意图。如果底片AB宽35mm,焦距是70mm,拍摄5m外的景物A′B ′有多宽?
70mm
5m
A
B
A′
O
B′
解:由题可知,
△ABO∽△A B O
∴
=
AB
A B
OD
OD
A B
=
35
70
5000
即
∴ A B =2500mm=2.5m
答:A B 的长为2.5m。
总结:
全等三角形与相似三角形性质比较
全等三角形 相似三角形
对应边________ 对应边______
对应角 _________ 对应角_______
对应中线 ____ 对应中线之比等于 ______
对应角平分线______ 对应角平分线之比等于____
对应高__________ 对应高之比等于 _______
定理 相似三角形对应高的比、对应角平分线的比、
对应中线的比都等于相似比.
相等
相等
相等
相等
相等
相等
成比例
相似比
相似比
相似比
作业:
名师测控22.3第1课时
谢 谢
22.3 相似三角形的性质
(1)什么叫相似三角形?什么是他们的相似比?
对应角相等、对应边成比例的三角形,叫做
相似三角形.
相似多边形对应边长度的比叫相似比
(2)如何判定两个三角形相似?
①两个角对应相等;
②两边对应成比例,且夹角相等;
③三边对应成比例.
回顾与复习
A
B
C
A/
B/
C/
①相似三角形的对应角
②相似三角形的对应边
想一想: 它们还有哪些性质呢
课前复习:
(3)相似三角形有何性质?
这一节重点研究相似三角形的性质。
相等
成比例
一个三角形有三条重要线段:____ __________
如果两个三角形全等,
那么这些对应线段有什么关系呢?
高、中线、角平分线
F
F
全等三角形对应线段(边、对应的高、中线、角平分线)相等。
如果两个三角形相似,
那么这些对应线段有什么关系呢?
F
在生活中,我们经常利用相似的知识解决建筑类问题.如图,小王依据图纸上的△ABC,以1:2的比例建造了模型房梁△A’B’C’,CD和C’D’分别是它们的立柱。
探究活动:
探究相似三角形对应高的比.
(1)试写出△ABC与△A’B’C’的对应边之间的关系,对应角之间的关系。
(2)你还能找到哪两个三角形相似 理由?
探究活动:
探究相似三角形对应高的比.
(3)如果CD=1.5cm,那么模型房的房梁立柱有多高?
(4)据此,你可以发现相似三角形怎样的性质?
探究活动:
探究相似三角形对应高的比.
猜想:相似三角形对应高的比等于相似比.
D'
C'
B'
A'
D
C
B
A
∽
推理及猜想:
结论:相似三角形对应高的比等于相似比.
类似结论
自主思考---
结论:相似三角形对应角的角平分线的比等于相似比.
类似结论
D'
C'
B'
A'
D
C
B
A
∽
自主思考---
结论:相似三角形对应中线的比等于相似比.
对应高的比
对应中线的比
对应角平分线的比
相
似
三
角
形
都等于相似比.
相似三角形的性质
定理 相似三角形对应高的比、对应角平分线的比、对应中线的比都等于相似比.
1.若两个相似三角形对应高的比为1:3,则这两个三角形的相似比是______
小试牛刀
1:3
2.△ABC∽△A’B’C’,AD和A’D’是
它们的对应角平分线,已知AD=4cm,
A’D’=10cm,那么对应高的比
是________
2:5
3、已知△ABC∽△DEF,BG、EH分△ABC和 △DEF的角平分线,BC=6cm,EF=4cm,BG=4.8cm.求EH的长.
小试牛刀
B
A
C
G
D
E
F
H
4.如图是一个照相机成像的示意图。如果底片AB宽35mm,焦距是70mm,拍摄5m外的景物A′B ′有多宽?
70mm
5m
A
B
A′
O
B′
解:由题可知,
△ABO∽△A B O
∴
=
AB
A B
OD
OD
A B
=
35
70
5000
即
∴ A B =2500mm=2.5m
答:A B 的长为2.5m。
总结:
全等三角形与相似三角形性质比较
全等三角形 相似三角形
对应边________ 对应边______
对应角 _________ 对应角_______
对应中线 ____ 对应中线之比等于 ______
对应角平分线______ 对应角平分线之比等于____
对应高__________ 对应高之比等于 _______
定理 相似三角形对应高的比、对应角平分线的比、
对应中线的比都等于相似比.
相等
相等
相等
相等
相等
相等
成比例
相似比
相似比
相似比
作业:
名师测控22.3第1课时
谢 谢
