华东师大版数学九年级上册 25.2.1 概率及其意义课件(共22张PPT)
文档属性
| 名称 | 华东师大版数学九年级上册 25.2.1 概率及其意义课件(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-05 21:02:12 | ||
图片预览








文档简介
(共22张PPT)
九年级数学上册·华师
第25章 随机事件的概率
25.2.1概率及其意义
第一课时
复习引入
(1)在地球上,水往低处流;
必然事件
不可能事件
(3)明天降雨
随机事件
如果天气预报说:“明天降雨的可能性是80%”,你出门会带雨具吗?
(2)某人的体温是100℃;
请指出下列事件是什么事件
(4)买到合格的足球
同一型号足球,甲厂合格率为99.9%,乙厂合格率为98.9%,若两产在价格等其它方面都相同,你愿意买哪个厂的产品?
复习引入
随机事件
知道了随机事件发生可能性的大小,对我们的生活有很大的指导作用!
探索新知
概率:一个事件发生的可能性就叫做该事件的概率
用P(事件)表示.
说明:
必然事件发生的概率为1,记作P(必然事件)=1;
不可能事件发生的概率为0,记作P(不可能事件)=0;
思考:
如果A为随机事件,你能确定P(A)的取值范围吗?
怎么来的?
0< P(A) <1
比如,抛掷一枚硬币,“正面向上”的概率为 ,记为:
P(正面向上)=
1
2
1
2
探索新知
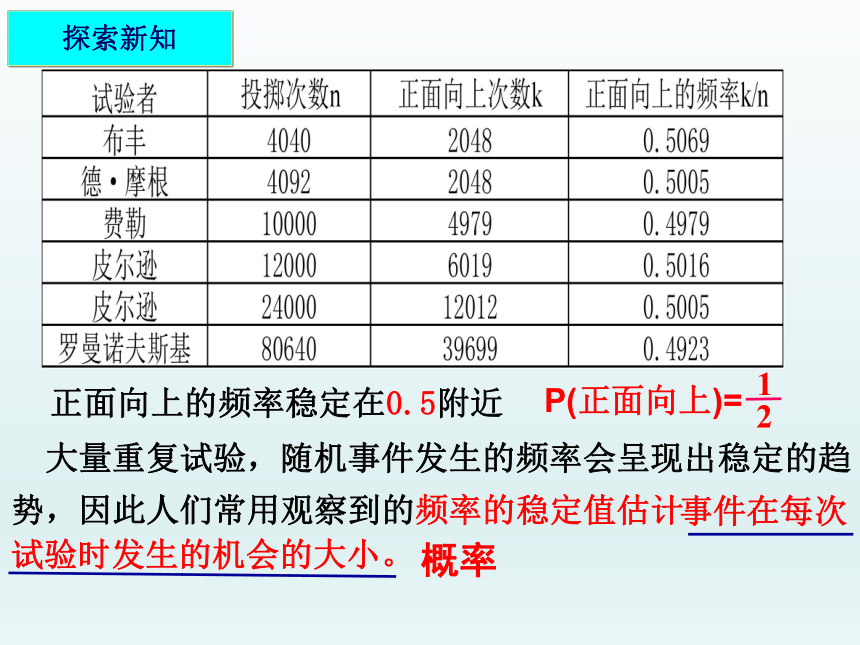
正面向上的频率稳定在0.5附近
大量重复试验,随机事件发生的频率会呈现出稳定的趋
势,因此人们常用观察到的频率的稳定值估计
事件在每次
试验时发生的机会的大小。
概率
P(正面向上)=
1
2
探索新知
需要大量重复试验
无法预测
缺点
思考:
在简单的问题情境下,我们能不能不实验,运用分析的方法预测概率?
求一个事件概率的基本方法是大量的重复试验,用频率稳定值估计概率
试验1:掷一枚 的硬币,落地后:
(2)每种结果出现的机会相等吗?
相等
两种
试验分析
(1)会出现几种结果?
质地均匀
(3)试分析:“正面向上”的概率为多少?
(3)试分析:掷得“6”的概率为多少?
6种
相等
(2)各结果出现的机会相等吗?
试验2:掷一枚 的正方体骰子,落地后:
(1)它落地时向上的点数有几种可能的结果?
质地均匀
所有结果可数,出现机会均等
试验分析
试验 关注的结果发生的概率 频率稳定值
掷一枚
硬币
投掷一正方体骰子
掷得“6”
关注的结果
所有 的结果
机会均等
正面向上
反面向上
正面向上
有2个
1个
掷得“1”,“2”,“3” “4”,“5”,
有6个
1个
“6”
一致
0.5
0.17
一致
小组探究
试验分析
试分析:抛掷一个质地均匀的正方体骰子,掷得点数是偶数的概率是多少?
试验3 关注的结果发生的概率 频率稳定值
投掷一正方体骰子 偶数
关注的结果
所有 的结果
机会均等
掷得“1”, ,“3”,
,“5”,
“2”
“6”
“4”
有6个
3个
试验分析
小组实验探究
小组内2人为一组,做投掷骰子的实验,要求:
(1)1个同学投掷骰子,1个同学记录;
(2)投掷骰子的同学每人每次只投掷一个,再由
记录的同学记下每次掷得的点数;
(3)骰子掉地不要捡,重新拿一个骰子继续投;
(4)一直做到老师喊结束为止。
试验分析
整理实验数据
1.数一数总共投掷骰子多少次,并把结果
填入表格最下面的汇总处;
2.在数据中找到并标出偶数点(2、4、6);
3.数一数偶数点共出现多少次,并把结果
填入表格最下面的汇总处;
4.小组内的三个数据汇总,即把掷骰子的总
数相加,出偶数点次数的总数相加。
表格1
试验3 关注的结果发生的概率
频率稳定值
投掷一正方体骰子 偶数
关注的结果
所有 的结果
机会均等
掷得“1”,“2”,“3”“4”,“5”,“6”
试验分析结论
0.5
一致
分析的方法预测概率
有6个
3个
概率公式
试验 关注的结果发生的概率
掷一枚
硬币
投掷一正方体骰子
掷得“6”
投掷一正方体骰子
偶数
正面向上
反面向上
反面向上
有2个
有6个
掷得“1”,“2”,“3”“4”,“5”,“6”
有1个
有1个
关注的
结果
所有机会均等的结果
掷得“1”,“2”,“3”“4”,“5”,“6”
有3个
有6个
你能找到计算概率的公式吗
个数
个数
方法归纳
概率的计算公式
P(关注的结果)=
关注结果的个数
所有机会均等结果的个数
概率公式
可能出现的结果只有有限个
各种结果出现的机会均等
前提条件
前提条件
关键点
清楚关注的结果是什么,个数有多少
清楚所有机会均等的结果有哪些,
个数是多少
练一练
1.袋中有3个红球,2个白球,从袋中任意摸
出1个球,则摸出白球的概率是
(2)P(抽到黑桃)=
把分数要化为最简形式
52张
2.从一副没有大小王的扑克牌中随机抽一张
(1)P(抽到A)=
4张
13张
2
5
4
52
1
13
13
52
1
4
=
=
也有同学说:正方体骰子质地均匀,出现各面的结果是等可能的,而“6”是其中一面,所以出现“6”的概率是 ,你同意这种说法吗?
有同学说:它表示每6次就有1次掷得“6”,你同意这种说法吗?
想一想:抛掷一枚正方形骰子,掷得“6”的概率等于 表示什么意思?
概率意义
错误.概率表示的是事件发生的可能性,并不是掷6次,就一定掷得点数“6”.
正确
这个同学用分析的方法得到掷得“6”的概率等于 ,但有解释它表示什么意思吗?
概率意义
实验探究
拿出刚才的实验数据,小组内三个负责记录的同学,分别找到第一次出现点数“6”的位置,然后数一数你是投掷几次才出现一次点数“6”的。
表格2
一旦掷得点数“6”就算完成一次试验
从实验结果看,掷得“6”的概率等于 的意义是:
如果买这个彩票很多很多张,那么平均每100张彩票有1张中奖。
概率意义
实验结论
例:彩票中奖的概率是 ,表示的意义是:
如果掷很多很多次,那么平均每6次有1次掷
得的点数是“6”
习题巩固
某小商店开展购物抽奖活动,规则:购物时每消费2元摸一次奖,每次摸奖时购物者从标有数字1、2、3、4、5的5个小球(小球之间只有号码不同)中摸出一球,若号码是2就中奖,奖品为一张精美图片。
(1)摸奖一次就得到一张精美图片的可能性是多少?
从大小形状一样的标有数字1、2、3、4、5的5个小球中摸出一球,摸到2号球的概率为
转化为数学问题
1
5
习题巩固
(2)小聪购买了10元的物品,前四次摸奖没有摸中,他想“第五次摸奖我一定能摸中”,你同意他的想法吗?说说你的看法?
(2)不同意,第五次摸到2号球是随机事件。
如果摸奖很多很多次,那么平均每5次有1次中奖
P(中奖)= 的意义是:
1
5
课堂小结
概率
概率的
概念
概率的
取值范围
0≤P(A)≤1
P(不可能事件)=0
P(必然事件)=1
概率的
意义
若A表示一个事件,则P(A)的范围是?
如果掷很多很多次的话,那么平均每2次有1次掷得正面
如:抛一枚硬币出现正面向上的概率等于
表示的意义是:
获得概率的方法
大量重复实验,频率的稳定值估计概率
分析
一个事件发生的可能性就叫做该事件的概率
用P(事件)表示.P要大写,事件要写清楚
布置作业
作 业
1、完成导学案
2、预习课本例1、例2、例3
3、课本P139练习(作业本)
请同学们认真完成作业!
九年级数学上册·华师
第25章 随机事件的概率
25.2.1概率及其意义
第一课时
复习引入
(1)在地球上,水往低处流;
必然事件
不可能事件
(3)明天降雨
随机事件
如果天气预报说:“明天降雨的可能性是80%”,你出门会带雨具吗?
(2)某人的体温是100℃;
请指出下列事件是什么事件
(4)买到合格的足球
同一型号足球,甲厂合格率为99.9%,乙厂合格率为98.9%,若两产在价格等其它方面都相同,你愿意买哪个厂的产品?
复习引入
随机事件
知道了随机事件发生可能性的大小,对我们的生活有很大的指导作用!
探索新知
概率:一个事件发生的可能性就叫做该事件的概率
用P(事件)表示.
说明:
必然事件发生的概率为1,记作P(必然事件)=1;
不可能事件发生的概率为0,记作P(不可能事件)=0;
思考:
如果A为随机事件,你能确定P(A)的取值范围吗?
怎么来的?
0< P(A) <1
比如,抛掷一枚硬币,“正面向上”的概率为 ,记为:
P(正面向上)=
1
2
1
2
探索新知
正面向上的频率稳定在0.5附近
大量重复试验,随机事件发生的频率会呈现出稳定的趋
势,因此人们常用观察到的频率的稳定值估计
事件在每次
试验时发生的机会的大小。
概率
P(正面向上)=
1
2
探索新知
需要大量重复试验
无法预测
缺点
思考:
在简单的问题情境下,我们能不能不实验,运用分析的方法预测概率?
求一个事件概率的基本方法是大量的重复试验,用频率稳定值估计概率
试验1:掷一枚 的硬币,落地后:
(2)每种结果出现的机会相等吗?
相等
两种
试验分析
(1)会出现几种结果?
质地均匀
(3)试分析:“正面向上”的概率为多少?
(3)试分析:掷得“6”的概率为多少?
6种
相等
(2)各结果出现的机会相等吗?
试验2:掷一枚 的正方体骰子,落地后:
(1)它落地时向上的点数有几种可能的结果?
质地均匀
所有结果可数,出现机会均等
试验分析
试验 关注的结果发生的概率 频率稳定值
掷一枚
硬币
投掷一正方体骰子
掷得“6”
关注的结果
所有 的结果
机会均等
正面向上
反面向上
正面向上
有2个
1个
掷得“1”,“2”,“3” “4”,“5”,
有6个
1个
“6”
一致
0.5
0.17
一致
小组探究
试验分析
试分析:抛掷一个质地均匀的正方体骰子,掷得点数是偶数的概率是多少?
试验3 关注的结果发生的概率 频率稳定值
投掷一正方体骰子 偶数
关注的结果
所有 的结果
机会均等
掷得“1”, ,“3”,
,“5”,
“2”
“6”
“4”
有6个
3个
试验分析
小组实验探究
小组内2人为一组,做投掷骰子的实验,要求:
(1)1个同学投掷骰子,1个同学记录;
(2)投掷骰子的同学每人每次只投掷一个,再由
记录的同学记下每次掷得的点数;
(3)骰子掉地不要捡,重新拿一个骰子继续投;
(4)一直做到老师喊结束为止。
试验分析
整理实验数据
1.数一数总共投掷骰子多少次,并把结果
填入表格最下面的汇总处;
2.在数据中找到并标出偶数点(2、4、6);
3.数一数偶数点共出现多少次,并把结果
填入表格最下面的汇总处;
4.小组内的三个数据汇总,即把掷骰子的总
数相加,出偶数点次数的总数相加。
表格1
试验3 关注的结果发生的概率
频率稳定值
投掷一正方体骰子 偶数
关注的结果
所有 的结果
机会均等
掷得“1”,“2”,“3”“4”,“5”,“6”
试验分析结论
0.5
一致
分析的方法预测概率
有6个
3个
概率公式
试验 关注的结果发生的概率
掷一枚
硬币
投掷一正方体骰子
掷得“6”
投掷一正方体骰子
偶数
正面向上
反面向上
反面向上
有2个
有6个
掷得“1”,“2”,“3”“4”,“5”,“6”
有1个
有1个
关注的
结果
所有机会均等的结果
掷得“1”,“2”,“3”“4”,“5”,“6”
有3个
有6个
你能找到计算概率的公式吗
个数
个数
方法归纳
概率的计算公式
P(关注的结果)=
关注结果的个数
所有机会均等结果的个数
概率公式
可能出现的结果只有有限个
各种结果出现的机会均等
前提条件
前提条件
关键点
清楚关注的结果是什么,个数有多少
清楚所有机会均等的结果有哪些,
个数是多少
练一练
1.袋中有3个红球,2个白球,从袋中任意摸
出1个球,则摸出白球的概率是
(2)P(抽到黑桃)=
把分数要化为最简形式
52张
2.从一副没有大小王的扑克牌中随机抽一张
(1)P(抽到A)=
4张
13张
2
5
4
52
1
13
13
52
1
4
=
=
也有同学说:正方体骰子质地均匀,出现各面的结果是等可能的,而“6”是其中一面,所以出现“6”的概率是 ,你同意这种说法吗?
有同学说:它表示每6次就有1次掷得“6”,你同意这种说法吗?
想一想:抛掷一枚正方形骰子,掷得“6”的概率等于 表示什么意思?
概率意义
错误.概率表示的是事件发生的可能性,并不是掷6次,就一定掷得点数“6”.
正确
这个同学用分析的方法得到掷得“6”的概率等于 ,但有解释它表示什么意思吗?
概率意义
实验探究
拿出刚才的实验数据,小组内三个负责记录的同学,分别找到第一次出现点数“6”的位置,然后数一数你是投掷几次才出现一次点数“6”的。
表格2
一旦掷得点数“6”就算完成一次试验
从实验结果看,掷得“6”的概率等于 的意义是:
如果买这个彩票很多很多张,那么平均每100张彩票有1张中奖。
概率意义
实验结论
例:彩票中奖的概率是 ,表示的意义是:
如果掷很多很多次,那么平均每6次有1次掷
得的点数是“6”
习题巩固
某小商店开展购物抽奖活动,规则:购物时每消费2元摸一次奖,每次摸奖时购物者从标有数字1、2、3、4、5的5个小球(小球之间只有号码不同)中摸出一球,若号码是2就中奖,奖品为一张精美图片。
(1)摸奖一次就得到一张精美图片的可能性是多少?
从大小形状一样的标有数字1、2、3、4、5的5个小球中摸出一球,摸到2号球的概率为
转化为数学问题
1
5
习题巩固
(2)小聪购买了10元的物品,前四次摸奖没有摸中,他想“第五次摸奖我一定能摸中”,你同意他的想法吗?说说你的看法?
(2)不同意,第五次摸到2号球是随机事件。
如果摸奖很多很多次,那么平均每5次有1次中奖
P(中奖)= 的意义是:
1
5
课堂小结
概率
概率的
概念
概率的
取值范围
0≤P(A)≤1
P(不可能事件)=0
P(必然事件)=1
概率的
意义
若A表示一个事件,则P(A)的范围是?
如果掷很多很多次的话,那么平均每2次有1次掷得正面
如:抛一枚硬币出现正面向上的概率等于
表示的意义是:
获得概率的方法
大量重复实验,频率的稳定值估计概率
分析
一个事件发生的可能性就叫做该事件的概率
用P(事件)表示.P要大写,事件要写清楚
布置作业
作 业
1、完成导学案
2、预习课本例1、例2、例3
3、课本P139练习(作业本)
请同学们认真完成作业!
