2021-2022学年高一下学期数学人教A版必修4 1.1.2弧度制 课件(共18张PPT)
文档属性
| 名称 | 2021-2022学年高一下学期数学人教A版必修4 1.1.2弧度制 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-05 11:05:55 | ||
图片预览




文档简介
(共18张PPT)
普通高中课程标准实验教科书(人教A版)必修4
1.1.2弧度制
你知道我们校园的占地面积吗?
“大糖衣”占地约255亩
总建筑面积约12.7万平方米
1公顷=15亩
1亩≈666.67平方米
度量单位是一个不变的量
不同的度量单位之间可以相互换算
根据实际情况,采用合适的度量单位
度量的本质
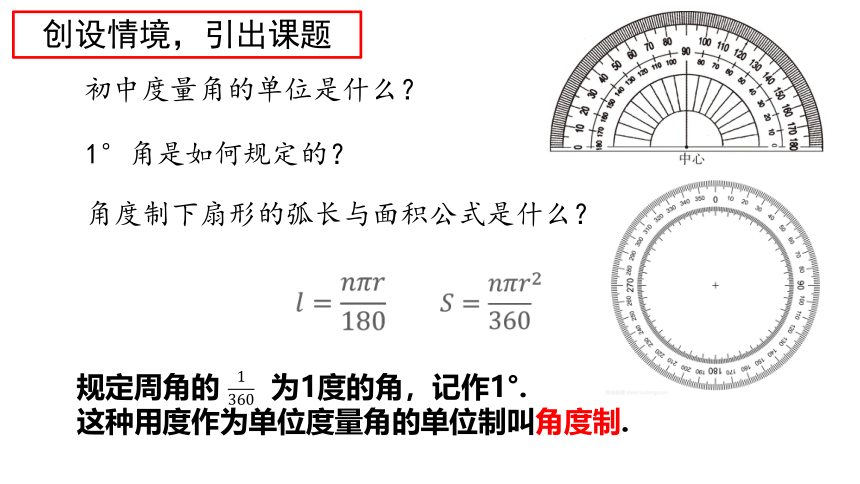
初中度量角的单位是什么?
1°角是如何规定的?
规定周角的 为1度的角,记作1°.
这种用度作为单位度量角的单位制叫角度制.
角度制下扇形的弧长与面积公式是什么?
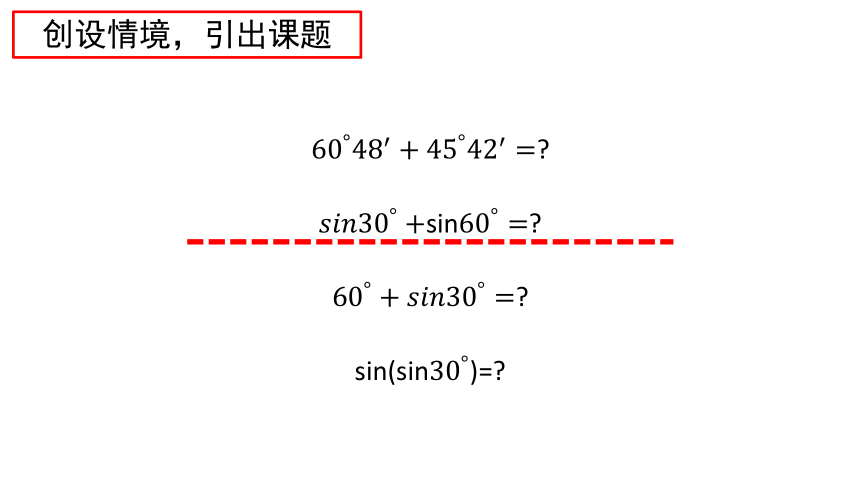
创设情境,引出课题
sin
sin(sin)=
创设情境,引出课题
sin
sin(sin)=
创设情境,引出课题
圆心角 半径r 弧长
1
2
3
圆心角 半径r 弧长
1
2
3
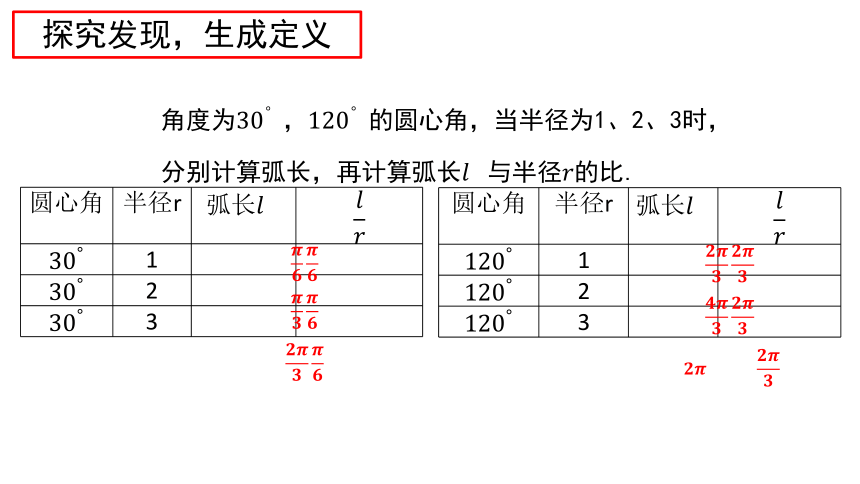
角度为的圆心角,当半径为1、2、3时,分别计算弧长,再计算弧长与半径的比.
探究发现,生成定义
圆心角固定,所对弧长与半径的比值是一个唯一确定的常数.
问题2:这个性质可以作为度量角的依据吗?
问题1:有什么发现?
圆心角所对弧长与半径的比值就是圆心角的弧度,
单位圆中就是圆心角的弧度就是所对弧的长度.
问题3:如何定义1弧度的角?
探究发现,生成定义
把长度等于半径长的弧所对的圆心角叫做1弧度的角,
记作1rad.
用“弧度”作为单位度量角制度叫弧度制.
1弧度角的定义
探究发现,生成定义
利用手中工具,做出1rad的圆心角
再做出2rad,
探索联系,巩固定义
问题4:角度制和弧度制都是角的度量制度,它们应该可以换算,
如何换算呢?
半径为r的圆的圆心与原点重合,角α的始边与x轴的非负半轴重合,交圆于点A,终边与圆交于点B.请在下列表格中填空.
x
y
O
弧长 OB旋转的方向 ∠AOB的弧度数 ∠AOB的角度数
r 逆时针方向
2r 逆时针方向
顺时针方向
顺时针方向
-180°
540°
新旧融合,知识建构
弧长 OB旋转的方向 ∠AOB的弧度数 ∠AOB的角度数
r 逆时针方向 180°
2r 逆时针方向 2 360°
顺时针方向 -1
顺时针方向 -2
0 不旋转 0
r 顺时针方向 - -180°
3r 逆时针方向 3 540°
问题5:如果
,
新旧融合,知识建构
角的集合与实数集R之间建立起了一一对应的关系
(1)把化成弧度(2)将rad换成角度
练习应用,理解定义
填写下列特殊角的度数和弧度数的对应表
练习应用,理解定义
利用弧度制证明下列关于扇形的公式:
(1) (2); (3).
已知扇形的半径为r,圆心角为,弧长为,面积为S
练习应用,理解定义
1.用自己的语言说一说弧度制的定义.
2.想一想弧度制和角度制的区别和联系
联系 区别 小提示
单位度(°)不能省略,而单位弧度(rad)通常省略不写
角度制 角的度量制度 可以相互换算 度量方法 进制 单位 弧度制 小结反思,形成思想
作业:
1.已知角α=1.5rad,β=85°,比较α与β的大小.
2.已知50cm的弧所对的圆心角为200°,求这条弧所在的圆的半径以及这个扇形的面积(可用计算器,结果保留一位小数).
3.(选做)每人准备一把扇子(自己做),然后与本小组其他同学对比,从中选出一把展开后看上去形状较为美观的扇子,并用计算器算出它的面积.
(1)假设这把扇子是从一个圆面中剪下的,而剩余部分的面积是,求与的比值;
(2)要使与的比值为0.618,则扇子的圆心角应为几度(精确到10°)?
普通高中课程标准实验教科书(人教A版)必修4
1.1.2弧度制
你知道我们校园的占地面积吗?
“大糖衣”占地约255亩
总建筑面积约12.7万平方米
1公顷=15亩
1亩≈666.67平方米
度量单位是一个不变的量
不同的度量单位之间可以相互换算
根据实际情况,采用合适的度量单位
度量的本质
初中度量角的单位是什么?
1°角是如何规定的?
规定周角的 为1度的角,记作1°.
这种用度作为单位度量角的单位制叫角度制.
角度制下扇形的弧长与面积公式是什么?
创设情境,引出课题
sin
sin(sin)=
创设情境,引出课题
sin
sin(sin)=
创设情境,引出课题
圆心角 半径r 弧长
1
2
3
圆心角 半径r 弧长
1
2
3
角度为的圆心角,当半径为1、2、3时,分别计算弧长,再计算弧长与半径的比.
探究发现,生成定义
圆心角固定,所对弧长与半径的比值是一个唯一确定的常数.
问题2:这个性质可以作为度量角的依据吗?
问题1:有什么发现?
圆心角所对弧长与半径的比值就是圆心角的弧度,
单位圆中就是圆心角的弧度就是所对弧的长度.
问题3:如何定义1弧度的角?
探究发现,生成定义
把长度等于半径长的弧所对的圆心角叫做1弧度的角,
记作1rad.
用“弧度”作为单位度量角制度叫弧度制.
1弧度角的定义
探究发现,生成定义
利用手中工具,做出1rad的圆心角
再做出2rad,
探索联系,巩固定义
问题4:角度制和弧度制都是角的度量制度,它们应该可以换算,
如何换算呢?
半径为r的圆的圆心与原点重合,角α的始边与x轴的非负半轴重合,交圆于点A,终边与圆交于点B.请在下列表格中填空.
x
y
O
弧长 OB旋转的方向 ∠AOB的弧度数 ∠AOB的角度数
r 逆时针方向
2r 逆时针方向
顺时针方向
顺时针方向
-180°
540°
新旧融合,知识建构
弧长 OB旋转的方向 ∠AOB的弧度数 ∠AOB的角度数
r 逆时针方向 180°
2r 逆时针方向 2 360°
顺时针方向 -1
顺时针方向 -2
0 不旋转 0
r 顺时针方向 - -180°
3r 逆时针方向 3 540°
问题5:如果
,
新旧融合,知识建构
角的集合与实数集R之间建立起了一一对应的关系
(1)把化成弧度(2)将rad换成角度
练习应用,理解定义
填写下列特殊角的度数和弧度数的对应表
练习应用,理解定义
利用弧度制证明下列关于扇形的公式:
(1) (2); (3).
已知扇形的半径为r,圆心角为,弧长为,面积为S
练习应用,理解定义
1.用自己的语言说一说弧度制的定义.
2.想一想弧度制和角度制的区别和联系
联系 区别 小提示
单位度(°)不能省略,而单位弧度(rad)通常省略不写
角度制 角的度量制度 可以相互换算 度量方法 进制 单位 弧度制 小结反思,形成思想
作业:
1.已知角α=1.5rad,β=85°,比较α与β的大小.
2.已知50cm的弧所对的圆心角为200°,求这条弧所在的圆的半径以及这个扇形的面积(可用计算器,结果保留一位小数).
3.(选做)每人准备一把扇子(自己做),然后与本小组其他同学对比,从中选出一把展开后看上去形状较为美观的扇子,并用计算器算出它的面积.
(1)假设这把扇子是从一个圆面中剪下的,而剩余部分的面积是,求与的比值;
(2)要使与的比值为0.618,则扇子的圆心角应为几度(精确到10°)?
