2021-2022学年高一上学期数学人教A版(2019)必修第一册-5.1.2弧度制 课件(共31张PPT)
文档属性
| 名称 | 2021-2022学年高一上学期数学人教A版(2019)必修第一册-5.1.2弧度制 课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 22.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-05 11:07:54 | ||
图片预览








文档简介
(共31张PPT)
5.1.2 弧度制
人教版高中数学必修第一册
一、创设情境,提出问题
问题1:某一黑洞距离太阳系约为5000万光年,请问能否用千米表示这个距离
5000 万光年 千米
千米.
1光年 千米
问题2:
一、创设情境,提出问题
问题3: 角怎么定义的?
二、问题驱动,探索新知
问题3: 角怎么定义的?
二、问题驱动,探索新知
问题3: 角怎么定义的?
二、问题驱动,探索新知
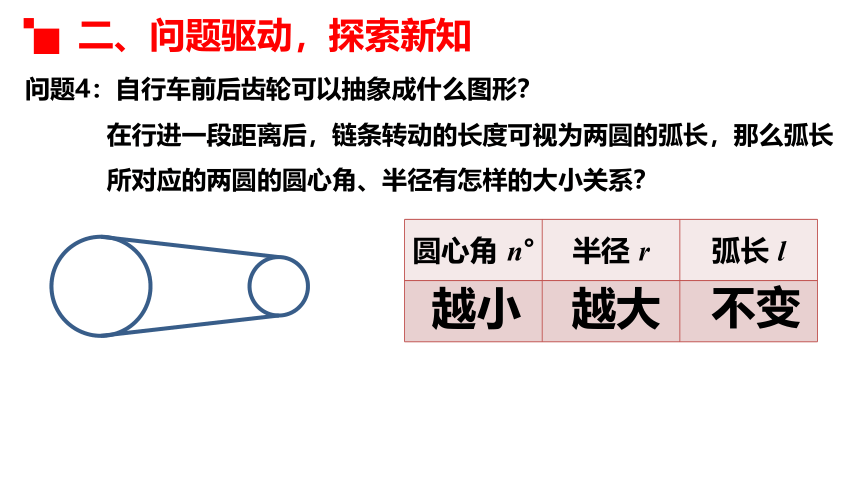
问题4:自行车前后齿轮可以抽象成什么图形?
二、问题驱动,探索新知
二、问题驱动,探索新知
圆心角 n° 半径 r 弧长 l
在行进一段距离后,链条转动的长度可视为两圆的弧长,那么弧长所对应的两圆的圆心角、半径有怎样的大小关系?
问题4:自行车前后齿轮可以抽象成什么图形?
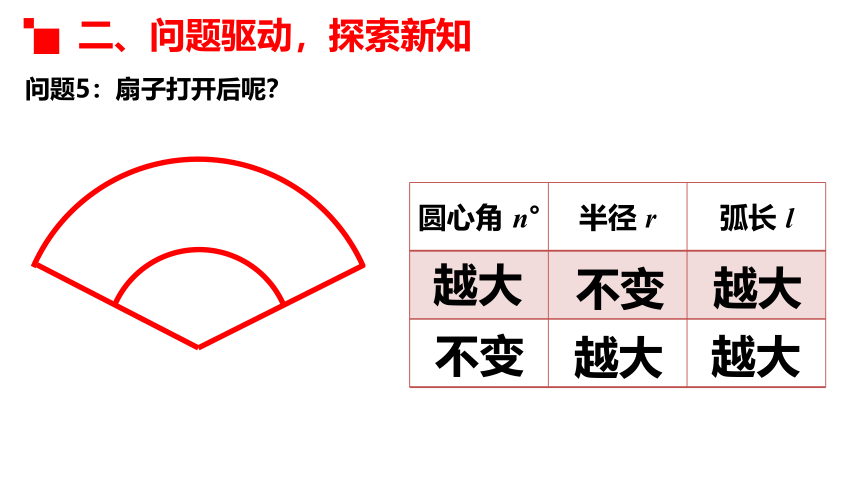
问题5:扇子打开过程中可以抽象成什么图形?
二、问题驱动,探索新知
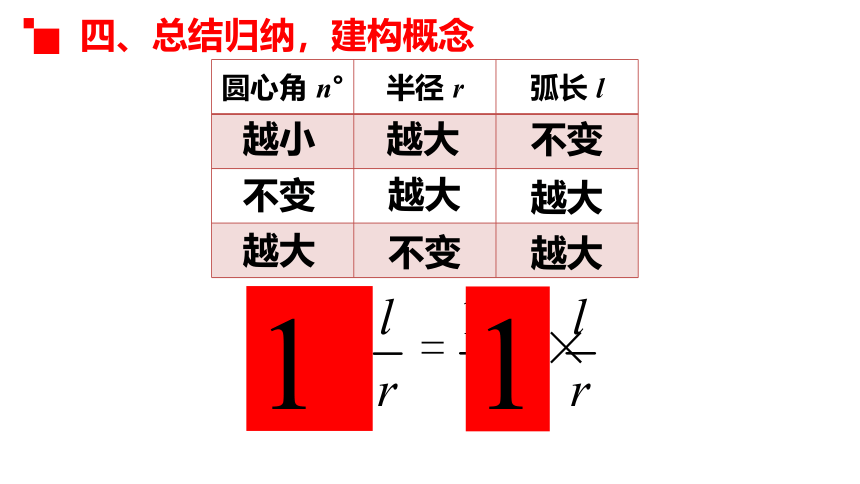
圆心角、半径、弧长中哪些没有变化?哪些变化?怎样变化?
圆心角 n° 半径 r 弧长 l
问题5:扇子打开后呢?
二、问题驱动,探索新知
圆心角 n° 半径 r 弧长 l
三、引入技术,科学验证
四、总结归纳,建构概念
圆心角 n° 半径 r 弧长 l
长度等于半径长的圆弧所对应的圆心角叫为1弧度(radian),单位用符号rad表示,读作弧度。
O
l=r
1rad
四、归纳总结,建构概念
1748年欧拉在它的著作《无穷小分析概论》中提出把圆的半径作为弧长的度量单位,这一思想将线段与弧的度量统一起来, 大大简化了三角的运算。
数学教师汤姆生首先使用了“弧度”一词,将“半径” (radius) 的前四个字母与“角”(angle)的前两个字母合在一起,构成radian,并被人们广泛接受和引用.
四、归纳总结,建构概念
O
l=r
四、归纳总结,建构概念
问题6:1rad ≈
1rad
60°
五、灵活转化,完善认知
弧长 l 圆心角 α
l=r 1
l=2r
2
五、灵活转化,完善认知
弧长 l 圆心角 α
l=r 1
l=2r 2
l=πr
π
五、灵活转化,完善认知
弧长 l 圆心角 α
l=r 1
l=2r 2
l=πr π
l=2πr
2π
五、灵活转化,完善认知
弧长 l 圆心角 α
l=r 1
l=2r 2
l=πr π
l=2πr 2π
l
l/r
弧长 l 圆心角 α
l=r 1
l=2r 2
l=πr π
l=2πr 2π
l
l/r
五、灵活转化,完善认知
写出一些特殊角对应的角度和弧度.
角度 -60° 0° 30° 60°
弧度
角度 120° 135° 270°
弧度
五、灵活转化,完善认知
正角
负角
零角
正实数
负实数
0
问题2:
六、回归情境,解决问题
>
问题6 若己知圆心角的弧度数 α 与半径 ,如何求扇形面积
六、回归情境,解决问题
六、回归情境,解决问题
角 角度制 弧度制
度量单位
单位规定
换算关系
弧长公式
扇形面积公式
弧度(10进制)
度(60进制)
长度等于半径的弧所对的圆心角叫做1弧度
圆周角的1/360叫做1°
问题7 用20cm长的铁丝围成一个扇形,应怎样设计才能使扇形的面积最大?最大面积是多少?
七、联系实际,学以致用
解:设扇形半径为rcm,
则弧长为(20-2r)cm
当且仅当r=5时,Smax=25
解:设扇形弧长为lcm,
则弧长为 cm
当且仅当l=10时,Smax=25
八、总结归纳,提炼概念
本节课你有哪些体会和收获?
八、总结归纳,提炼概念
九、课后检测,拓展延伸
一、基础过关
1、一条弦的长等于半径,这条弦所对的圆心角等于1弧度么?为什么?
2、把下列角度化成弧度
(1)36° (2)-150° (3)1095° (4)1440°
3、把下列弧度化成角度
(1) (2) (3) (4)
九、课后检测,拓展延伸
能力提升
4、已知互相啮合的两个齿轮,大轮有48齿,小轮有20齿.
(1)当大轮转动一周时,求小轮转动的角度;
(2)如果大轮的转速为 180r/min(转/分),小轮的半径为10.5cm,那么小轮周上一点每 1s 转过的弧长是多少?
九、课后检测,拓展延伸
二、实践创新
请同学们自主组建兴趣小组,上网查阅资料,根据不同材质的价格、产生的风量大小等,设计一把优秀的扇子,开展一次数学建模和数学探究的活动,每个人把研究成果和心得撰写成一篇数学建模小论文。
谢 谢!
5.1.2 弧度制
人教版高中数学必修第一册
一、创设情境,提出问题
问题1:某一黑洞距离太阳系约为5000万光年,请问能否用千米表示这个距离
5000 万光年 千米
千米.
1光年 千米
问题2:
一、创设情境,提出问题
问题3: 角怎么定义的?
二、问题驱动,探索新知
问题3: 角怎么定义的?
二、问题驱动,探索新知
问题3: 角怎么定义的?
二、问题驱动,探索新知
问题4:自行车前后齿轮可以抽象成什么图形?
二、问题驱动,探索新知
二、问题驱动,探索新知
圆心角 n° 半径 r 弧长 l
在行进一段距离后,链条转动的长度可视为两圆的弧长,那么弧长所对应的两圆的圆心角、半径有怎样的大小关系?
问题4:自行车前后齿轮可以抽象成什么图形?
问题5:扇子打开过程中可以抽象成什么图形?
二、问题驱动,探索新知
圆心角、半径、弧长中哪些没有变化?哪些变化?怎样变化?
圆心角 n° 半径 r 弧长 l
问题5:扇子打开后呢?
二、问题驱动,探索新知
圆心角 n° 半径 r 弧长 l
三、引入技术,科学验证
四、总结归纳,建构概念
圆心角 n° 半径 r 弧长 l
长度等于半径长的圆弧所对应的圆心角叫为1弧度(radian),单位用符号rad表示,读作弧度。
O
l=r
1rad
四、归纳总结,建构概念
1748年欧拉在它的著作《无穷小分析概论》中提出把圆的半径作为弧长的度量单位,这一思想将线段与弧的度量统一起来, 大大简化了三角的运算。
数学教师汤姆生首先使用了“弧度”一词,将“半径” (radius) 的前四个字母与“角”(angle)的前两个字母合在一起,构成radian,并被人们广泛接受和引用.
四、归纳总结,建构概念
O
l=r
四、归纳总结,建构概念
问题6:1rad ≈
1rad
60°
五、灵活转化,完善认知
弧长 l 圆心角 α
l=r 1
l=2r
2
五、灵活转化,完善认知
弧长 l 圆心角 α
l=r 1
l=2r 2
l=πr
π
五、灵活转化,完善认知
弧长 l 圆心角 α
l=r 1
l=2r 2
l=πr π
l=2πr
2π
五、灵活转化,完善认知
弧长 l 圆心角 α
l=r 1
l=2r 2
l=πr π
l=2πr 2π
l
l/r
弧长 l 圆心角 α
l=r 1
l=2r 2
l=πr π
l=2πr 2π
l
l/r
五、灵活转化,完善认知
写出一些特殊角对应的角度和弧度.
角度 -60° 0° 30° 60°
弧度
角度 120° 135° 270°
弧度
五、灵活转化,完善认知
正角
负角
零角
正实数
负实数
0
问题2:
六、回归情境,解决问题
>
问题6 若己知圆心角的弧度数 α 与半径 ,如何求扇形面积
六、回归情境,解决问题
六、回归情境,解决问题
角 角度制 弧度制
度量单位
单位规定
换算关系
弧长公式
扇形面积公式
弧度(10进制)
度(60进制)
长度等于半径的弧所对的圆心角叫做1弧度
圆周角的1/360叫做1°
问题7 用20cm长的铁丝围成一个扇形,应怎样设计才能使扇形的面积最大?最大面积是多少?
七、联系实际,学以致用
解:设扇形半径为rcm,
则弧长为(20-2r)cm
当且仅当r=5时,Smax=25
解:设扇形弧长为lcm,
则弧长为 cm
当且仅当l=10时,Smax=25
八、总结归纳,提炼概念
本节课你有哪些体会和收获?
八、总结归纳,提炼概念
九、课后检测,拓展延伸
一、基础过关
1、一条弦的长等于半径,这条弦所对的圆心角等于1弧度么?为什么?
2、把下列角度化成弧度
(1)36° (2)-150° (3)1095° (4)1440°
3、把下列弧度化成角度
(1) (2) (3) (4)
九、课后检测,拓展延伸
能力提升
4、已知互相啮合的两个齿轮,大轮有48齿,小轮有20齿.
(1)当大轮转动一周时,求小轮转动的角度;
(2)如果大轮的转速为 180r/min(转/分),小轮的半径为10.5cm,那么小轮周上一点每 1s 转过的弧长是多少?
九、课后检测,拓展延伸
二、实践创新
请同学们自主组建兴趣小组,上网查阅资料,根据不同材质的价格、产生的风量大小等,设计一把优秀的扇子,开展一次数学建模和数学探究的活动,每个人把研究成果和心得撰写成一篇数学建模小论文。
谢 谢!
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
