黑龙江省哈尔滨市第一六二中学2021-2022学年高三上学期第三次月考(12月)数学(理)试题(Word版含答案)
文档属性
| 名称 | 黑龙江省哈尔滨市第一六二中学2021-2022学年高三上学期第三次月考(12月)数学(理)试题(Word版含答案) | 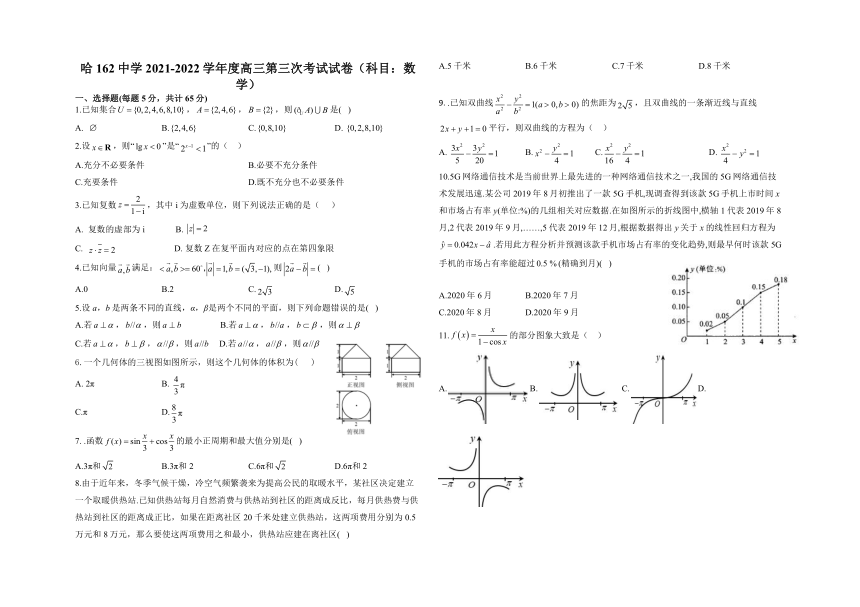 | |
| 格式 | docx | ||
| 文件大小 | 526.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-04 20:45:01 | ||
图片预览


文档简介
哈162中学2021-2022学年度高三第三次考试试卷(科目:数学)
一、选择题(每题5分,共计65分)
1.已知集合,,,则是( )
A. B. C. D.
2.设,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.已知复数,其中i为虚数单位,则下列说法正确的是( )
A. 复数的虚部为i B.
C. D. 复数Z在复平面内对应的点在第四象限
4.已知向量满足:则( )
A.0 B.2 C. D.
5.设a,b是两条不同的直线,α,β是两个不同的平面,则下列命题错误的是( )
A.若,,则 B.若,,,则
C.若,,,则 D.若,,则
6.一个几何体的三视图如图所示,则这个几何体的体积为( )
A. 2π B.
C.π D.
7. .函数的最小正周期和最大值分别是( )
A.3π和 B.3π和2 C.6π和 D.6π和2
8.由于近年来,冬季气候干燥,冷空气频繁袭来为提高公民的取暖水平,某社区决定建立一个取暖供热站.已知供热站每月自然消费与供热站到社区的距离成反比,每月供热费与供热站到社区的距离成正比,如果在距离社区20千米处建立供热站,这两项费用分别为0.5万元和8万元,那么要使这两项费用之和最小,供热站应建在离社区( )
A.5千米 B.6千米 C.7千米 D.8千米
9. .已知双曲线的焦距为,且双曲线的一条渐近线与直线平行,则双曲线的方程为( )
A. B. C. D.
10.5G网络通信技术是当前世界上最先进的一种网络通信技术之一,我国的5G网络通信技术发展迅速.某公司2019年8月初推出了一款5G手机,现调查得到该款5G手机上市时间x和市场占有率y(单位:%)的几组相关对应数据.在如图所示的折线图中,横轴1代表2019年8月,2代表2019年9月,……,5代表2019年12月,根据数据得出y关于x的线性回归方程为.若用此方程分析并预测该款手机市场占有率的变化趋势,则最早何时该款5G手机的市场占有率能超过(精确到月)( )
A.2020年6月 B.2020年7月
C.2020年8月 D.2020年9月
11.的部分图象大致是( )
A.B.C.D.
12.已知椭圆的左,右焦点分别为,,过且与x轴垂直的直线交椭圆于A,B两点,直线与椭圆的另一个交点为C,若,则椭圆的离心率为( )
A. B. C. D.
13.已知函数,若函数恰有3个零点,则实数m的取值范围是( )
A. B. C. D.
二、填空题(每题5分,共计25分)
14.曲线在点处的切线方程是__________.
15.自2019年12月以来,在湖北省武汉市发现多起病毒性肺炎病例,研究表明,该新型冠状病毒具有很强的传染性各级政府反应迅速,采取了有效的防控阻击措施,把疫情控制在最低范围之内.某社区按上级要求做好在鄂返乡人员体格检查登记,有3个不同的住户属在鄂返乡住户,负责该小区体格检查的社区诊所共有4名医生,现要求这4名医生都要分配出去,且每个住户家里都要有医生去检查登记,则不同的分配方案共有_________种.(用数字作答)
16.的展开式中含的系数为,则的值为__________
17.设等差数列的前n项和为.若,,则__________
已知三棱锥中,平面ABC,且,,,则三棱的外接球的表面积为_________.
三.解答题
19.(满分12分)的内角A,B,C的对边分别为a,b,c,已知.
(1)求B;(2)若,的面积为,求的周长.
20.(满分12分)已知等比数列的前项和为,且,.
(1)求的通项公式;
(2)求.
21.(满分14分)如图,在三棱柱中,侧面为正方形,,分别是,的中点,平面.
(1)求证:平面平面;
(2)求证:平面;
(3)若是边长为2的菱形,求直线与平面所成角的正弦值.
22.(满分12分)年支付宝“集五福”活动从月日开始,持续到月11日.用户打开支付宝最新版,通过AR扫描“福”字集福卡(爱国福、富强福、和谐福、友善福和敬业福).在除夕夜前集齐“五福”的用户将获得一个现金红包.为调查居民参与“集五福”活动的情况,现对某一社区的居民进行抽样调查,并按年龄(单位:岁)分成,,,,五组,得到如图所示的频率分布直方图,其中年龄在内的人数为.
集齐“五福”卡 没有集齐“五福”卡 合计
男
女
合计
(1)假设未参与的视为未集齐“五福”者,请根据样本数据补充完整上述列联表,并判断是否有的把握认为是否集齐“五福”与性别相关.
(2)为了解该社区居民明年是否愿意继续参与此活动,现从样本中年龄在和内的人中,采用分层抽样的方法抽取人,再从中随机抽取人进行调查,求抽取到的人中恰好有人的年龄在内的概率.
参考公式:,其中.
参考数据:
23.(满分10分)在直角坐标系xOy中,直线l的参数方程为(t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为.
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)若直线l与曲线C交于M,N两点,设,求的值.
参考答案
1-13DACBD BCABC AAB
14.x-y-2=0
15.36
16.-1
17.32
18.32
19.解:(1),
由正弦定理得:,
整理得:,
∵在中,,∴,
即,∴,即;
(2)由余弦定理得:,
∴,∵,
∴,∴,∴,∴的周长为.
20解:设的公比为,
因为,,则,
又因为,解得,
所以的通项公式为.
(2)解:由,可得,
则,
所以.
21.证明:(1)平面,平面,,
正方形,,
,平面,
平面,平面平面.
(2)设中点为,连结,,
,分别是,的中点,,且,
又,,,且
,且,四边形为平行四边形,,
平面,平面,平面.
(3)由(1)知,,两两互相垂直,以为原点,
,,分别为轴,轴,轴,建立空间直角坐标系,
是边长为2的菱形,为的中点,且,
,,0,,,0,,,,,,0,,
,,,,,,,,,,0,,
,,,,0,,,,,
设平面的法向量,,,
则,令,则,
设直线与平面所成角为,
则.
直线与平面所成角的正弦值为.
22(1)由题意可知参与“集五福”活动的人数为.
列联表补充如下:
集齐“五福”卡 没有集齐“五福”卡 合计
男
女
合计
因为,所以有的把握认为是否集齐“五福”与性别相关.
(2)由频率分布直方图可知,年龄在内的人数是,
年龄在内的人数是.
从中随机抽取名,年龄在内的人数是,记为;
年龄在内的人数是,记为,,.
从这人中随机抽取人的情况有,,,,,,共种;
其中符合条件的情况有,,,共种.
故所求概率.
23. (1),
(2)
一、选择题(每题5分,共计65分)
1.已知集合,,,则是( )
A. B. C. D.
2.设,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.已知复数,其中i为虚数单位,则下列说法正确的是( )
A. 复数的虚部为i B.
C. D. 复数Z在复平面内对应的点在第四象限
4.已知向量满足:则( )
A.0 B.2 C. D.
5.设a,b是两条不同的直线,α,β是两个不同的平面,则下列命题错误的是( )
A.若,,则 B.若,,,则
C.若,,,则 D.若,,则
6.一个几何体的三视图如图所示,则这个几何体的体积为( )
A. 2π B.
C.π D.
7. .函数的最小正周期和最大值分别是( )
A.3π和 B.3π和2 C.6π和 D.6π和2
8.由于近年来,冬季气候干燥,冷空气频繁袭来为提高公民的取暖水平,某社区决定建立一个取暖供热站.已知供热站每月自然消费与供热站到社区的距离成反比,每月供热费与供热站到社区的距离成正比,如果在距离社区20千米处建立供热站,这两项费用分别为0.5万元和8万元,那么要使这两项费用之和最小,供热站应建在离社区( )
A.5千米 B.6千米 C.7千米 D.8千米
9. .已知双曲线的焦距为,且双曲线的一条渐近线与直线平行,则双曲线的方程为( )
A. B. C. D.
10.5G网络通信技术是当前世界上最先进的一种网络通信技术之一,我国的5G网络通信技术发展迅速.某公司2019年8月初推出了一款5G手机,现调查得到该款5G手机上市时间x和市场占有率y(单位:%)的几组相关对应数据.在如图所示的折线图中,横轴1代表2019年8月,2代表2019年9月,……,5代表2019年12月,根据数据得出y关于x的线性回归方程为.若用此方程分析并预测该款手机市场占有率的变化趋势,则最早何时该款5G手机的市场占有率能超过(精确到月)( )
A.2020年6月 B.2020年7月
C.2020年8月 D.2020年9月
11.的部分图象大致是( )
A.B.C.D.
12.已知椭圆的左,右焦点分别为,,过且与x轴垂直的直线交椭圆于A,B两点,直线与椭圆的另一个交点为C,若,则椭圆的离心率为( )
A. B. C. D.
13.已知函数,若函数恰有3个零点,则实数m的取值范围是( )
A. B. C. D.
二、填空题(每题5分,共计25分)
14.曲线在点处的切线方程是__________.
15.自2019年12月以来,在湖北省武汉市发现多起病毒性肺炎病例,研究表明,该新型冠状病毒具有很强的传染性各级政府反应迅速,采取了有效的防控阻击措施,把疫情控制在最低范围之内.某社区按上级要求做好在鄂返乡人员体格检查登记,有3个不同的住户属在鄂返乡住户,负责该小区体格检查的社区诊所共有4名医生,现要求这4名医生都要分配出去,且每个住户家里都要有医生去检查登记,则不同的分配方案共有_________种.(用数字作答)
16.的展开式中含的系数为,则的值为__________
17.设等差数列的前n项和为.若,,则__________
已知三棱锥中,平面ABC,且,,,则三棱的外接球的表面积为_________.
三.解答题
19.(满分12分)的内角A,B,C的对边分别为a,b,c,已知.
(1)求B;(2)若,的面积为,求的周长.
20.(满分12分)已知等比数列的前项和为,且,.
(1)求的通项公式;
(2)求.
21.(满分14分)如图,在三棱柱中,侧面为正方形,,分别是,的中点,平面.
(1)求证:平面平面;
(2)求证:平面;
(3)若是边长为2的菱形,求直线与平面所成角的正弦值.
22.(满分12分)年支付宝“集五福”活动从月日开始,持续到月11日.用户打开支付宝最新版,通过AR扫描“福”字集福卡(爱国福、富强福、和谐福、友善福和敬业福).在除夕夜前集齐“五福”的用户将获得一个现金红包.为调查居民参与“集五福”活动的情况,现对某一社区的居民进行抽样调查,并按年龄(单位:岁)分成,,,,五组,得到如图所示的频率分布直方图,其中年龄在内的人数为.
集齐“五福”卡 没有集齐“五福”卡 合计
男
女
合计
(1)假设未参与的视为未集齐“五福”者,请根据样本数据补充完整上述列联表,并判断是否有的把握认为是否集齐“五福”与性别相关.
(2)为了解该社区居民明年是否愿意继续参与此活动,现从样本中年龄在和内的人中,采用分层抽样的方法抽取人,再从中随机抽取人进行调查,求抽取到的人中恰好有人的年龄在内的概率.
参考公式:,其中.
参考数据:
23.(满分10分)在直角坐标系xOy中,直线l的参数方程为(t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为.
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)若直线l与曲线C交于M,N两点,设,求的值.
参考答案
1-13DACBD BCABC AAB
14.x-y-2=0
15.36
16.-1
17.32
18.32
19.解:(1),
由正弦定理得:,
整理得:,
∵在中,,∴,
即,∴,即;
(2)由余弦定理得:,
∴,∵,
∴,∴,∴,∴的周长为.
20解:设的公比为,
因为,,则,
又因为,解得,
所以的通项公式为.
(2)解:由,可得,
则,
所以.
21.证明:(1)平面,平面,,
正方形,,
,平面,
平面,平面平面.
(2)设中点为,连结,,
,分别是,的中点,,且,
又,,,且
,且,四边形为平行四边形,,
平面,平面,平面.
(3)由(1)知,,两两互相垂直,以为原点,
,,分别为轴,轴,轴,建立空间直角坐标系,
是边长为2的菱形,为的中点,且,
,,0,,,0,,,,,,0,,
,,,,,,,,,,0,,
,,,,0,,,,,
设平面的法向量,,,
则,令,则,
设直线与平面所成角为,
则.
直线与平面所成角的正弦值为.
22(1)由题意可知参与“集五福”活动的人数为.
列联表补充如下:
集齐“五福”卡 没有集齐“五福”卡 合计
男
女
合计
因为,所以有的把握认为是否集齐“五福”与性别相关.
(2)由频率分布直方图可知,年龄在内的人数是,
年龄在内的人数是.
从中随机抽取名,年龄在内的人数是,记为;
年龄在内的人数是,记为,,.
从这人中随机抽取人的情况有,,,,,,共种;
其中符合条件的情况有,,,共种.
故所求概率.
23. (1),
(2)
同课章节目录
