沪科版数学九年级上册 21.5 反比例函数教学设计
文档属性
| 名称 | 沪科版数学九年级上册 21.5 反比例函数教学设计 |
|
|
| 格式 | docx | ||
| 文件大小 | 75.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-05 00:00:00 | ||
图片预览

文档简介
反比例函数教学设计
一、自我检测,激活旧知归
1、点(3,-1)在反比例函数y=(k≠0)的图像上,则k的值是( )
A、3 B、-3 C、 D、-
2、若双曲线y=的图像:
(1)位于第二、四象限,则k的取值范围是_________________
(2)在每个象限内,y随x的增大而减小,则k的取值范围是___________
3、已知点A(2,y1)、B(4,y2)都在反比例函数y=的图像上,则y1与y2的大小关系为_______________
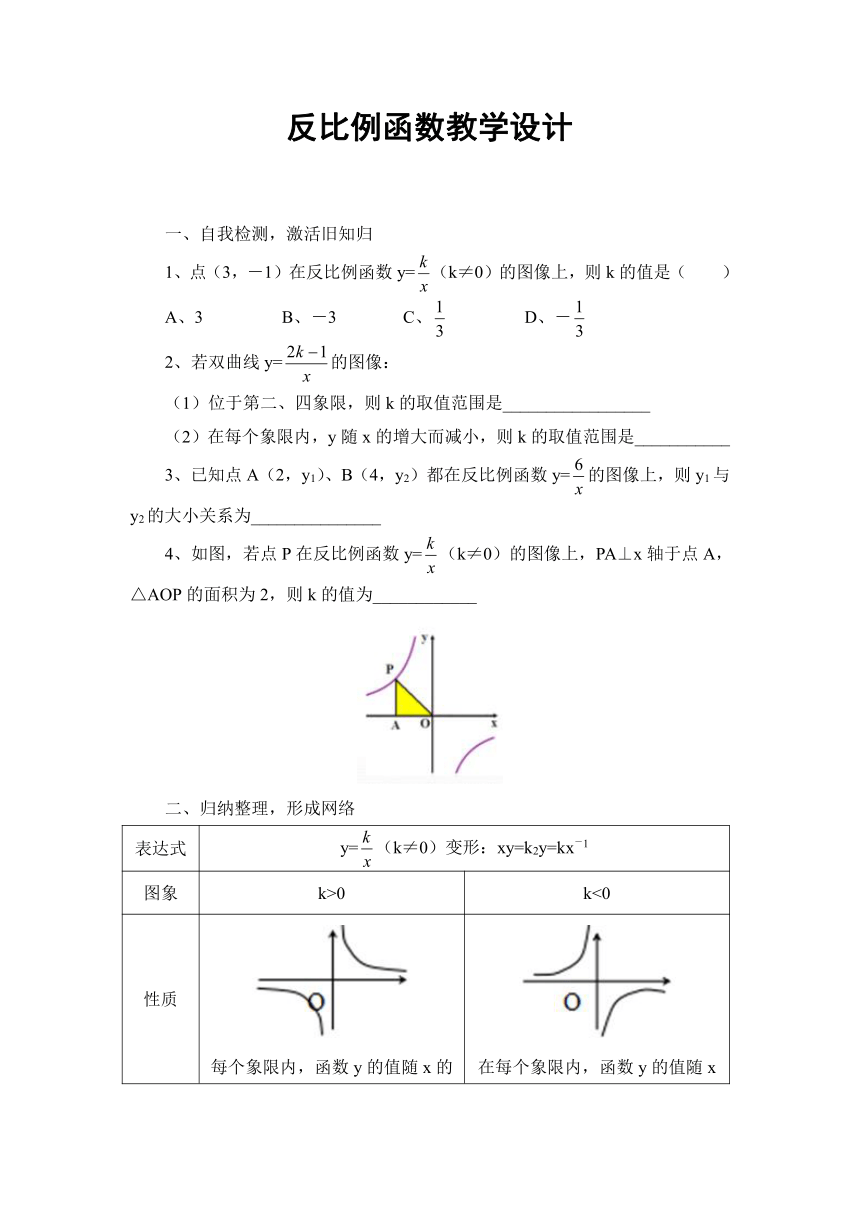
4、如图,若点P在反比例函数y=(k≠0)的图像上,PA⊥x轴于点A,△AOP的面积为2,则k的值为____________
二、归纳整理,形成网络
表达式 y=(k≠0)变形:xy=k2y=kx-1
图象 k>0 k<0
性质 每个象限内,函数y的值随x的增大而减小。 在每个象限内,函数y的值随x的增大而增大。
k的几何意义:S矩=|k|,S△=|k|
反比例函数的图象是中心对称图形,以坐标原点为对称中心。反比例函数的图象是轴对称图形。
三、例题讲解,感受方法
例1.如图,已知反比例函数y1=与一次函数y2=k2x+b的图象交于点A(1,8)、B(-4,m).
(1)求k1、k2、b的值;
(2)写出y1>y2时,x的取值范围;
(3)求△AOB的面积.
例2.工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800℃,然后停止煅烧进行锻造操作,经过8min时,材料温度降为600℃。煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系(如图).已知该材料初始温度是32℃。
(1)分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于480℃时,须停止操作.那么锻造的操作时间有多长?
四、巩固练习,形成能力
1、在一个可以改变改变体积的密闭容器内装有一定质量的某种气体,当改变容器的体积时,气体的密度也会随之改变,密度ρ(单位:kg/m2)与体积V(单位:m3)满足函数关系式ρ=(k为常数,k≠0),其图像如图所示,则k的值为( )
A、9 B、-9
C、4 D、-4
2、已知反比例函数y=,当-4≤x≤-1时,y的取值范围是___________
3、已知直线y=-4x与双曲线y=的一个交点的坐标为(m,-2),则它们的另一个交点坐标是____________
4、已知一次函数y1=-x-1的图像与反比例函数y2=的图像交于点交于A点,A点的横坐标为2,求A点的坐标及反比例函数的解析式.
五、课堂总结,归纳提升
1、通过本节课复习,你回顾了哪些知识?
2、你有什么感悟和体会?例
一、自我检测,激活旧知归
1、点(3,-1)在反比例函数y=(k≠0)的图像上,则k的值是( )
A、3 B、-3 C、 D、-
2、若双曲线y=的图像:
(1)位于第二、四象限,则k的取值范围是_________________
(2)在每个象限内,y随x的增大而减小,则k的取值范围是___________
3、已知点A(2,y1)、B(4,y2)都在反比例函数y=的图像上,则y1与y2的大小关系为_______________
4、如图,若点P在反比例函数y=(k≠0)的图像上,PA⊥x轴于点A,△AOP的面积为2,则k的值为____________
二、归纳整理,形成网络
表达式 y=(k≠0)变形:xy=k2y=kx-1
图象 k>0 k<0
性质 每个象限内,函数y的值随x的增大而减小。 在每个象限内,函数y的值随x的增大而增大。
k的几何意义:S矩=|k|,S△=|k|
反比例函数的图象是中心对称图形,以坐标原点为对称中心。反比例函数的图象是轴对称图形。
三、例题讲解,感受方法
例1.如图,已知反比例函数y1=与一次函数y2=k2x+b的图象交于点A(1,8)、B(-4,m).
(1)求k1、k2、b的值;
(2)写出y1>y2时,x的取值范围;
(3)求△AOB的面积.
例2.工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800℃,然后停止煅烧进行锻造操作,经过8min时,材料温度降为600℃。煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系(如图).已知该材料初始温度是32℃。
(1)分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于480℃时,须停止操作.那么锻造的操作时间有多长?
四、巩固练习,形成能力
1、在一个可以改变改变体积的密闭容器内装有一定质量的某种气体,当改变容器的体积时,气体的密度也会随之改变,密度ρ(单位:kg/m2)与体积V(单位:m3)满足函数关系式ρ=(k为常数,k≠0),其图像如图所示,则k的值为( )
A、9 B、-9
C、4 D、-4
2、已知反比例函数y=,当-4≤x≤-1时,y的取值范围是___________
3、已知直线y=-4x与双曲线y=的一个交点的坐标为(m,-2),则它们的另一个交点坐标是____________
4、已知一次函数y1=-x-1的图像与反比例函数y2=的图像交于点交于A点,A点的横坐标为2,求A点的坐标及反比例函数的解析式.
五、课堂总结,归纳提升
1、通过本节课复习,你回顾了哪些知识?
2、你有什么感悟和体会?例
