2021-2022学年人教版数学七年级上册3.3解一元一次方程(二)-去括号与去分母(1)课件(18张)
文档属性
| 名称 | 2021-2022学年人教版数学七年级上册3.3解一元一次方程(二)-去括号与去分母(1)课件(18张) |  | |
| 格式 | zip | ||
| 文件大小 | 51.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-05 19:29:54 | ||
图片预览




文档简介
(共18张PPT)
复习旧知
解下列方程:
1. 3x+5=4x+1
2. 9-3y=5y+5
解得:x=4
解得:y=
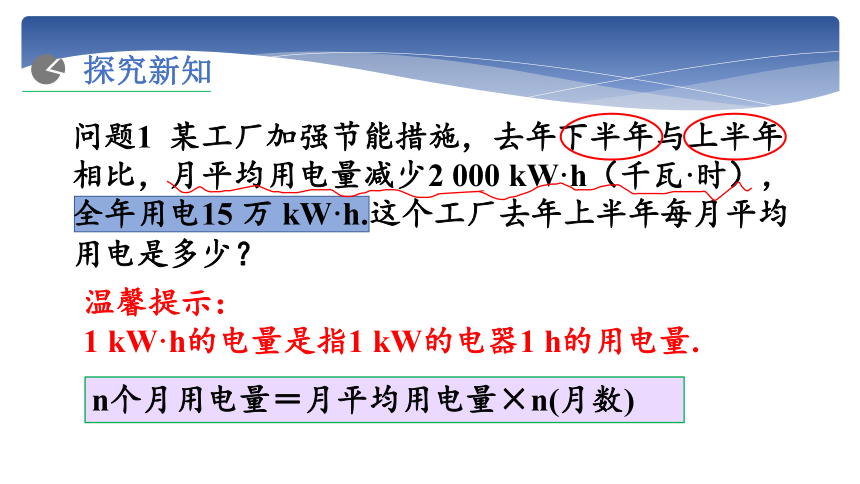
问题1 某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2 000 kW·h(千瓦·时),全年用电15 万 kW·h.这个工厂去年上半年每月平均用电是多少?
温馨提示:
1 kW·h的电量是指1 kW的电器1 h的用电量.
n个月用电量=月平均用电量×n(月数)
探究新知
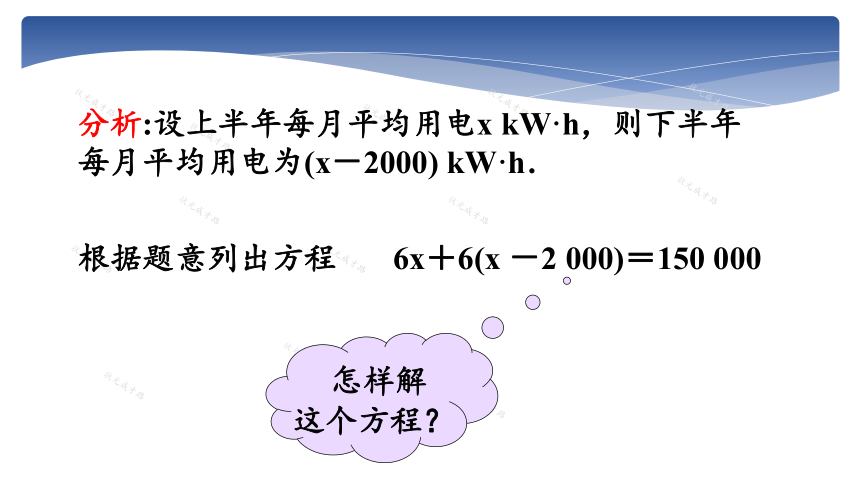
分析:设上半年每月平均用电x kW·h,则下半年每月平均用电为(x-2000) kW·h.
6x+6(x -2 000)=150 000
根据题意列出方程
怎样解这个方程?
教师:白帆
新疆教科研
微信公众号
3.3 解一元一次方程(二)
——去括号与去分母
第1课时 去括号
6x+6(x-2 000)=150 000
6x+6x-12 000=150 000
6x+6x=150 000+12 000
12x=162 000
x=13 500
去括号
合并同类项
移项
系数化为1
本题还有其他列方程的方法吗?用其他方法列出的方程应怎样解?
合作交流
思考
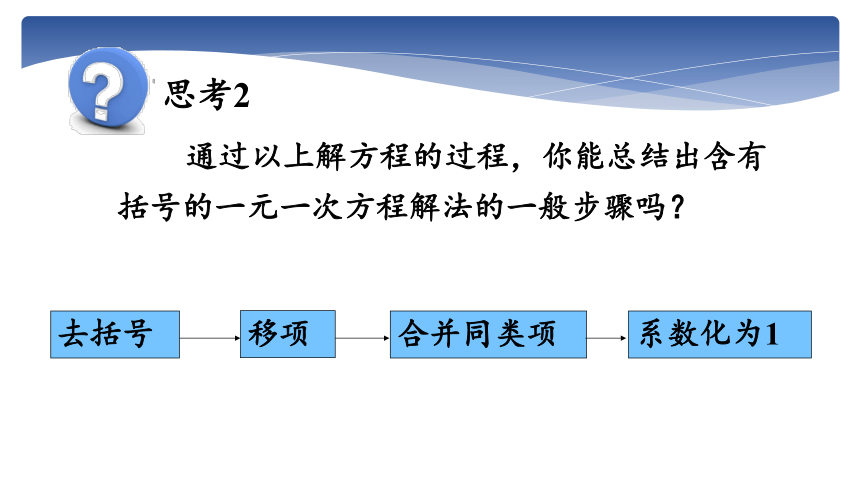
通过以上解方程的过程,你能总结出含有括号的一元一次方程解法的一般步骤吗?
去括号
移项
合并同类项
系数化为1
思考2
例1 解下列方程:
(1)2x –(x + 10)= 5x + 2(x – 1);
解:去括号,得
2x – x – 10 = 5x +2x – 2
移项,得
2x – x – 5x – 2x = – 2 + 10
合并同类项,得
– 6x = 8
系数化为1,得
探究新知
(2)3x – 7(x – 1)= 3 – 2(x + 3)
解:去括号,得
移项,得
合并同类项,得
–2x = –10
系数化为1,得
3x – 7x + 7= 3 – 2x – 6
3x – 7x + 2x= 3 – 6 – 7
x = 5
巩固练习
解:去括号,得
移项,得
合并同类项,得
–2x=0
系数化为1,得
x=0
(2)2–3(x+1)=1–2(1+0.5x)
2–3x–3=1–2–x
–3x+x=1–2–2+3
解下列方程
解:去括号,得
2x + 6 = 5x
移项,得
2x–5x = –6
合并同类项,得
–3x = –6
系数化为1,得
x = 2
(1)2(x+3)=5x
例2 一艘船从甲码头到乙码头顺流而行,用了2 h;从乙码头返回甲码头逆流而行,用了2.5 h.已知水流的速度是3 km/h,求船在静水中的速度.
分析:找等量关系这艘船往返的路程相等,
顺流速度__顺流时间__逆流速度__逆流时间 .
解:设船在静水中的平均速度为x km/h,则顺流的速度为(x+3) km/h,逆流速度为(x-3) km/h.
探究新知
×
×
=
根据往返路程相等,列得
去括号,得
移项及合并同类项,得
系数化为1,得
答:船在静水中的平均速度为 27 km/h.
2(x + 3)= 2.5(x – 3).
2x + 6 = 2.5x – 7.5.
0.5x = 13.5.
x = 27.
基础检测
1. 解方程3-(x+6)=-5(x-1)时,去括号正确的是( ).
A.3-x+6=-5x+5 B.3-x-6=-5x+5
C.3-x+6=-5x-5 D.3-x-6=-5x+1
2. 对方程 25b–(b–5)=29
去括号,得_____________________,
移项,得___________________,
合并同类项,得______________,
系数化为1,得____________.
25b – b + 5 = 29
25b – b = 29-5
24b = 24
b = 1
B
今年“双十一”,小红用8.8元钱购买了甲、乙两种礼物,甲礼物每件1.2元,乙礼物每件0.8元,其中甲礼物比乙礼物少1件,问甲、乙两种礼物各买了多少件?
解:设小红购买甲礼物x件,则购买乙礼物(x+1)件,
根据题意,得 1.2x+0.8(x+1)=8.8,
解得, x=4,
所以 x+1=5.
答:甲种礼物买了4件,乙种礼物买了5件.
综合应用
当x为何值时,式子3(x-2)和4(x+3)-4相等.
能力提升
3(x-2)=4(x+3)-4
步骤
去括号→移项→合并同类项→系数化为1.
理 论 依 据
(等式的性质1) (等式的性质2)
课堂小结
去括号解一元一次方程
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
谢谢倾听
敬请指导
复习旧知
解下列方程:
1. 3x+5=4x+1
2. 9-3y=5y+5
解得:x=4
解得:y=
问题1 某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2 000 kW·h(千瓦·时),全年用电15 万 kW·h.这个工厂去年上半年每月平均用电是多少?
温馨提示:
1 kW·h的电量是指1 kW的电器1 h的用电量.
n个月用电量=月平均用电量×n(月数)
探究新知
分析:设上半年每月平均用电x kW·h,则下半年每月平均用电为(x-2000) kW·h.
6x+6(x -2 000)=150 000
根据题意列出方程
怎样解这个方程?
教师:白帆
新疆教科研
微信公众号
3.3 解一元一次方程(二)
——去括号与去分母
第1课时 去括号
6x+6(x-2 000)=150 000
6x+6x-12 000=150 000
6x+6x=150 000+12 000
12x=162 000
x=13 500
去括号
合并同类项
移项
系数化为1
本题还有其他列方程的方法吗?用其他方法列出的方程应怎样解?
合作交流
思考
通过以上解方程的过程,你能总结出含有括号的一元一次方程解法的一般步骤吗?
去括号
移项
合并同类项
系数化为1
思考2
例1 解下列方程:
(1)2x –(x + 10)= 5x + 2(x – 1);
解:去括号,得
2x – x – 10 = 5x +2x – 2
移项,得
2x – x – 5x – 2x = – 2 + 10
合并同类项,得
– 6x = 8
系数化为1,得
探究新知
(2)3x – 7(x – 1)= 3 – 2(x + 3)
解:去括号,得
移项,得
合并同类项,得
–2x = –10
系数化为1,得
3x – 7x + 7= 3 – 2x – 6
3x – 7x + 2x= 3 – 6 – 7
x = 5
巩固练习
解:去括号,得
移项,得
合并同类项,得
–2x=0
系数化为1,得
x=0
(2)2–3(x+1)=1–2(1+0.5x)
2–3x–3=1–2–x
–3x+x=1–2–2+3
解下列方程
解:去括号,得
2x + 6 = 5x
移项,得
2x–5x = –6
合并同类项,得
–3x = –6
系数化为1,得
x = 2
(1)2(x+3)=5x
例2 一艘船从甲码头到乙码头顺流而行,用了2 h;从乙码头返回甲码头逆流而行,用了2.5 h.已知水流的速度是3 km/h,求船在静水中的速度.
分析:找等量关系这艘船往返的路程相等,
顺流速度__顺流时间__逆流速度__逆流时间 .
解:设船在静水中的平均速度为x km/h,则顺流的速度为(x+3) km/h,逆流速度为(x-3) km/h.
探究新知
×
×
=
根据往返路程相等,列得
去括号,得
移项及合并同类项,得
系数化为1,得
答:船在静水中的平均速度为 27 km/h.
2(x + 3)= 2.5(x – 3).
2x + 6 = 2.5x – 7.5.
0.5x = 13.5.
x = 27.
基础检测
1. 解方程3-(x+6)=-5(x-1)时,去括号正确的是( ).
A.3-x+6=-5x+5 B.3-x-6=-5x+5
C.3-x+6=-5x-5 D.3-x-6=-5x+1
2. 对方程 25b–(b–5)=29
去括号,得_____________________,
移项,得___________________,
合并同类项,得______________,
系数化为1,得____________.
25b – b + 5 = 29
25b – b = 29-5
24b = 24
b = 1
B
今年“双十一”,小红用8.8元钱购买了甲、乙两种礼物,甲礼物每件1.2元,乙礼物每件0.8元,其中甲礼物比乙礼物少1件,问甲、乙两种礼物各买了多少件?
解:设小红购买甲礼物x件,则购买乙礼物(x+1)件,
根据题意,得 1.2x+0.8(x+1)=8.8,
解得, x=4,
所以 x+1=5.
答:甲种礼物买了4件,乙种礼物买了5件.
综合应用
当x为何值时,式子3(x-2)和4(x+3)-4相等.
能力提升
3(x-2)=4(x+3)-4
步骤
去括号→移项→合并同类项→系数化为1.
理 论 依 据
(等式的性质1) (等式的性质2)
课堂小结
去括号解一元一次方程
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
谢谢倾听
敬请指导
