2021-2022学年苏科版数学八年级下册9.4.2菱形课件(38张)
文档属性
| 名称 | 2021-2022学年苏科版数学八年级下册9.4.2菱形课件(38张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-05 19:33:55 | ||
图片预览









文档简介
(共38张PPT)
9.4.2 菱形
第9章 中心对称图形——平行四边形
新知一 菱形的定义及其性质
1. 定义
有一组邻边相等的平行四边形叫做菱形.
合作探究
2. 特殊性质如下表
图形 文字语言(性质) 符号语言
菱形的四条边都相等 ∵四边形ABCD 是菱形,
∴ AB=BC=CD=AD
菱形的两条对角线互相垂直 ∵四边形ABCD 是菱形,
∴ BD ⊥ AC
菱形既是轴对称图形,有两条对称轴,又是中心对称图形
(1)菱形的性质可以用来证明线段相等,角相等,直线平行、垂直以及进行相关的计算;
(2)菱形的性质与勾股定理联系,可得对角线长与边长之间的关系,即边长的平方等于两条对角线长一半的平方和;
(3)如果菱形的一个内角为60°,那么菱形的两条边与较短的对角线构成的三角形为等边三角形;
(4)菱形的面积= 底× 高= 两条对角线长乘积的一半(填空题、选择题直接运用).
特别提醒:
1. 菱形必须满足两个条件:一是平行四边形;二是一组邻边相等.二者必须同时具备,缺一不可.
2. 菱形的定义既是菱形的基本性质,也是菱形的基本判定方法.
3. 菱形是特殊的平行四边形,它具有平行四边形的一切性质,如对边平行且相等,对角相等,对角线互相平分.
3. 矩形和菱形的区别
(1)矩形和菱形都是建立在平行四边形的基础上,矩形是附加一直角,而菱形是附加一组邻边相等;
(2)矩形的两条对角线把矩形分割成四个面积相等的等腰三角形,而菱形的两条对角线把菱形分割成四个全等的直角三角形;
(3)矩形的对称轴是两条过两组对边中点的直线,而菱形的对称轴是两条对角线所在的直线.
例 1
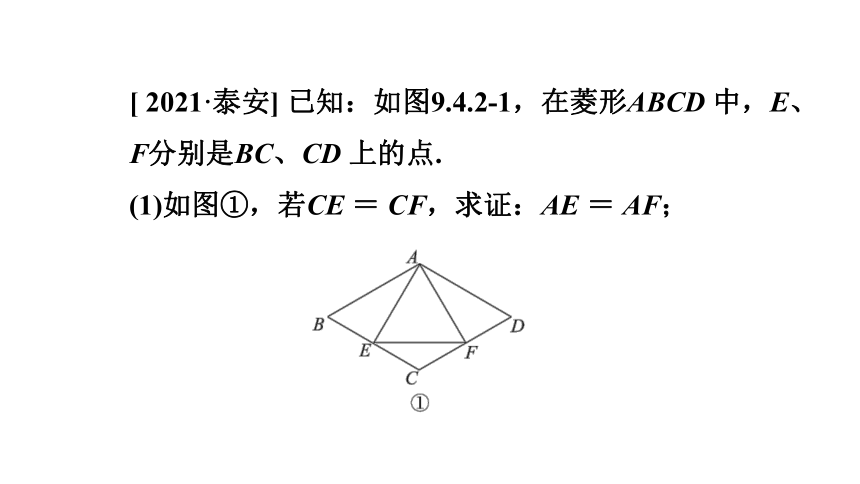
[ 2021·泰安] 已知:如图9.4.2-1,在菱形ABCD 中,E、F分别是BC、CD 上的点.
(1)如图①,若CE = CF,求证:AE = AF;
证明:∵四边形ABCD 为菱形,
∴∠ B =∠ D,AB = BC = CD = DA(菱形的对角相等,四条边相等).又∵ CE = CF,∴ BE = DF.
在△ ABE 和△ ADF 中,
AB=AD,
∠ B= ∠ D,
BE=DF,
∴△ ABE ≌△ ADF.∴ AE = AF.
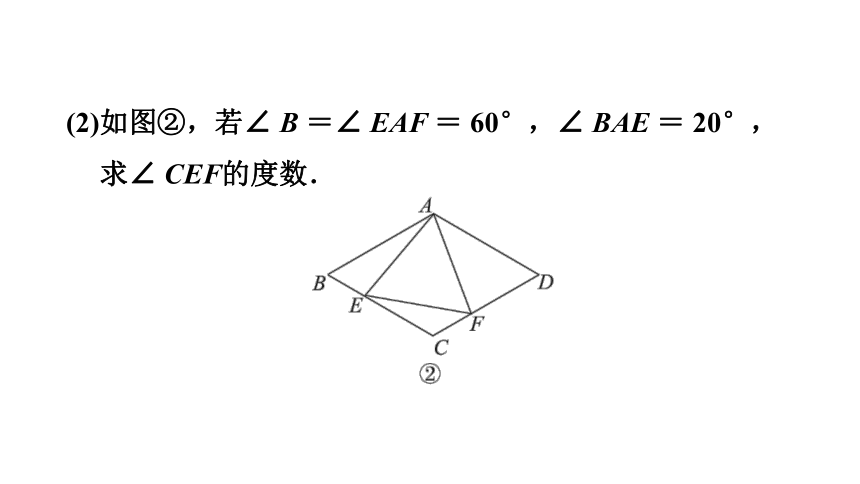
(2)如图②,若∠ B =∠ EAF = 60°,∠ BAE = 20°,求∠ CEF的度数.
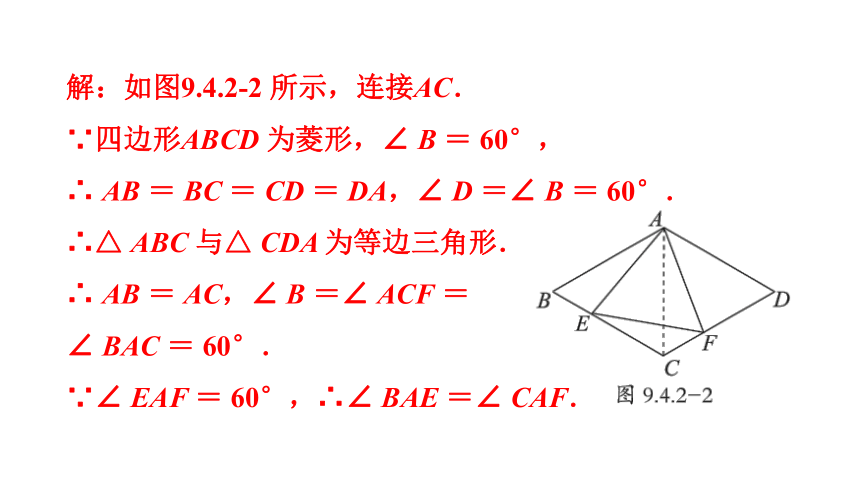
解:如图9.4.2-2 所示,连接AC.
∵四边形ABCD 为菱形,∠ B = 60°,
∴ AB = BC = CD = DA,∠ D =∠ B = 60°.
∴△ ABC 与△ CDA 为等边三角形.
∴ AB = AC,∠ B =∠ ACF =
∠ BAC = 60°.
∵∠ EAF = 60°,∴∠ BAE =∠ CAF.
在△ ABE 和△ ACF 中,
∠ BAE= ∠ CAF,
AB=AC,
∠ B= ∠ ACF,
∴△ ABE ≌△ ACF.∴ AE = AF.∵∠ EAF = 60°,∴△ EAF 为等边三角形.∴∠ AEF = 60°.
∵∠ AEC =∠ B+ ∠ BAE =∠ AEF+ ∠ CEF,
∴ 60° +20°= 60° + ∠ CEF.∴∠ CEF = 20°.
在菱形中如果出现“30 °“”60 °“”120 °“”一边等于最短对角线”这些词语时,往往都指向等边三角形,我们需用等边三角形的知识来解决.
新知二 菱形的判定
1. 判定
图形 文字语言(判定) 符号语言
有一组邻边相等的平行四边形叫做菱形(定义法) ∵ AB=BC(或AB=AD 或AD=CD 或BC=CD)
∴ ABCD 是菱形
四边相等的四边形是菱形(判定1) ∵ AB=BC=AD=CD,
∴四边形ABCD 是菱形
对角线互相垂直的平行四边形是菱形(判定2) ∵ AC ⊥ BD.
∴ ABCD 是菱形
2. 易错警示 判定菱形时,一定要明确前提是从“四边形”出发的,还是从“平行四边形”出发的:(1)若从“四边形”出发,则还需四条边相等;(2)若从“平行四边形”出发,则还需一组邻边相等或对角线互相垂直.
特别提醒:
1.菱形的判定定理和性质定理是互逆定理.
2.判定菱形的常见思路
四
边
形
可依据题目特点选取不同的方法.
四条边都相等→菱形对角线互相垂直且平分→菱形
平行四边形
对角线互相垂直→菱形
有一组邻边相等→菱形
例2
已知:如图9.4.2-3,在△ ABC 中,CD 平分∠ ACB 交AB 于点D,DE ∥ AC 交BC 于点E,DF ∥ BC 交AC 于点F. 四边形DECF 是菱形吗?为什么?
解:四边形DECF 是菱形. 理由如下:
∵ DE ∥ FC,DF ∥ EC,
∴四边形DECF 为平行四边形.∵ AC ∥ DE,∴∠ 2= ∠ 3.
∵ CD 平分∠ ACB,∴∠ 1= ∠ 2. ∴∠ 1= ∠ 3.
∴ DE=EC.
∴平行四边形DECF 为菱形(有一组邻边相等的平行四边形是菱形).
解法提醒:
菱形的定义既是菱形的性质,也是菱形的一种判定方法.
在用菱形的定义判定一个四边形是菱形时,首先判定这个四边形是平行四边形,再证一组邻边相等.
平行
四边形
一组邻边相等
菱形
例 3
如图9.4.2-4,在平行四边形ABCD 中,对角线AC、BD 相交于点O,过点O 作直线EF ⊥ BD,分别交AD、BC 于点E 和点F,连接BE、DF. 求证:四边形BEDF 是菱形.
证明:∵四边形ABCD 是平行四边形,
∴ OB=OD,AD ∥ BC.
∴∠ EDO= ∠ FBO,∠ OED= ∠ OFB.
∴△ OED ≌△ OFB. ∴ DE=BF.
又∵ DE ∥ BF,∴四边形BEDF 是平行四边形.
∵ EF ⊥ BD,
∴平行四边形BEDF 是菱形(对角线互相垂直的平行四边形是菱形).
解法点拨:
证明一个四边形是菱形的方法:
若已知要证的四边形的对角线互相垂直,则要考虑证明这个四边形是平行四边形,用“对角线互相垂直的平行四边形是菱形”进行证明.
平行
四边形
对角线互
相垂直
菱形
例4
如图9.4.2-5,在Rt △ ACB 中,∠ ACB=90°,
∠ BAC=60°,DE 垂直平分BC,垂足为D,交AB 于点E,点F 在DE 的延长线上,且AF=CE. 求证:四边形ACEF 是菱形.
证明:∵ DE 垂直平分BC,∴ BE=CE.
∵∠ ACB=90° , ∠ BAC=60° ,
∴∠ BCE= ∠ B=30° . ∴∠ ACE=60° .
∴△ ACE 为等边三角形. ∴ AE=CE=AC.
∵∠ AEF= ∠ BED=90° - ∠ B=60°,AF=CE=AE,
∴△ AEF 为等边三角形.
∴ AE=AF=EF. ∴ AC=CE=EF=AF.
∴四边形ACEF 是菱形(四条边相等的四边形是菱形).
方法点拨:
有较多线段相等的条件时,我们可考虑通过证明四条边相等来证明这个四边形是菱形.注意:本例也可以先证四边形ACEF是平行四边形,再证一组邻边相等,只不过步骤复杂一点,读者不妨试一试.
如图,若要使 ABCD成为菱形,则需要添加的条件是( )
A.AB=CD
B.AD=AC
C.AB=BC
D.AC=BD
1
C
巩固新知
【2020·武威】如图所示的木制活动衣帽架由三个全等的菱形构成,根据实际需要可以调节A,E间的距离.若A,E间的距离调节到60 cm,菱形的边长AB=20 cm,则∠DAB的度数是( )
A.90°
B.100°
C.120°
D.150°
C
2
如图,菱形ABCD的周长是4 cm,∠ABC=60°,那么这个菱形的对角线AC的长是( )
A.1 cm
B.2 cm
C.3 cm
D.4 cm
3
A
【2021·河南】关于菱形的性质,以下说法不正确的是( )
A.四条边相等 B.对角线相等
C.对角线互相垂直 D.是轴对称图形
4
B
如图,菱形ABCD的对角线AC,BD相交于点O,过点D作DH⊥AB于点H,连接OH,若OA=6,OH=4,则菱形ABCD的面积为( )
A.72
B.24
C.48
D.96
5
C
6
D
7
B
【2021·广安】如图,四边形ABCD是菱形,点E,F分别在边AB,AD的延长线上,且BE=DF.连接CE,CF.
求证:CE=CF.
8
如图,在菱形ABCD中,点P是BC边上一点,连接AP,点E,F是AP上的两点,连接DE,BF,使得∠AED=∠ABC,∠ABF=∠BPF.
9
求证:(1)△ABF≌△DAE;
证明:∵四边形ABCD是菱形,
∴AB=AD,AD∥BC.∴∠BPA=∠DAE.
∵∠ABC=∠AED,∴∠BAF=∠ADE.
∵∠ABF=∠BPF,∴∠ABF=∠DAE.
∴△ABF≌△DAE(ASA).
(2)DE=BF+EF.
证明:∵△ABF≌△DAE,
∴BF=AE,AF=DE.
∴AF=AE+EF=BF+EF.∴DE=BF+EF.
菱形
菱形
边的性质
性质
角的性质
对角线的性质
定义
判定
边的关系
对称性
对角线关系
归纳新知
再见
9.4.2 菱形
第9章 中心对称图形——平行四边形
新知一 菱形的定义及其性质
1. 定义
有一组邻边相等的平行四边形叫做菱形.
合作探究
2. 特殊性质如下表
图形 文字语言(性质) 符号语言
菱形的四条边都相等 ∵四边形ABCD 是菱形,
∴ AB=BC=CD=AD
菱形的两条对角线互相垂直 ∵四边形ABCD 是菱形,
∴ BD ⊥ AC
菱形既是轴对称图形,有两条对称轴,又是中心对称图形
(1)菱形的性质可以用来证明线段相等,角相等,直线平行、垂直以及进行相关的计算;
(2)菱形的性质与勾股定理联系,可得对角线长与边长之间的关系,即边长的平方等于两条对角线长一半的平方和;
(3)如果菱形的一个内角为60°,那么菱形的两条边与较短的对角线构成的三角形为等边三角形;
(4)菱形的面积= 底× 高= 两条对角线长乘积的一半(填空题、选择题直接运用).
特别提醒:
1. 菱形必须满足两个条件:一是平行四边形;二是一组邻边相等.二者必须同时具备,缺一不可.
2. 菱形的定义既是菱形的基本性质,也是菱形的基本判定方法.
3. 菱形是特殊的平行四边形,它具有平行四边形的一切性质,如对边平行且相等,对角相等,对角线互相平分.
3. 矩形和菱形的区别
(1)矩形和菱形都是建立在平行四边形的基础上,矩形是附加一直角,而菱形是附加一组邻边相等;
(2)矩形的两条对角线把矩形分割成四个面积相等的等腰三角形,而菱形的两条对角线把菱形分割成四个全等的直角三角形;
(3)矩形的对称轴是两条过两组对边中点的直线,而菱形的对称轴是两条对角线所在的直线.
例 1
[ 2021·泰安] 已知:如图9.4.2-1,在菱形ABCD 中,E、F分别是BC、CD 上的点.
(1)如图①,若CE = CF,求证:AE = AF;
证明:∵四边形ABCD 为菱形,
∴∠ B =∠ D,AB = BC = CD = DA(菱形的对角相等,四条边相等).又∵ CE = CF,∴ BE = DF.
在△ ABE 和△ ADF 中,
AB=AD,
∠ B= ∠ D,
BE=DF,
∴△ ABE ≌△ ADF.∴ AE = AF.
(2)如图②,若∠ B =∠ EAF = 60°,∠ BAE = 20°,求∠ CEF的度数.
解:如图9.4.2-2 所示,连接AC.
∵四边形ABCD 为菱形,∠ B = 60°,
∴ AB = BC = CD = DA,∠ D =∠ B = 60°.
∴△ ABC 与△ CDA 为等边三角形.
∴ AB = AC,∠ B =∠ ACF =
∠ BAC = 60°.
∵∠ EAF = 60°,∴∠ BAE =∠ CAF.
在△ ABE 和△ ACF 中,
∠ BAE= ∠ CAF,
AB=AC,
∠ B= ∠ ACF,
∴△ ABE ≌△ ACF.∴ AE = AF.∵∠ EAF = 60°,∴△ EAF 为等边三角形.∴∠ AEF = 60°.
∵∠ AEC =∠ B+ ∠ BAE =∠ AEF+ ∠ CEF,
∴ 60° +20°= 60° + ∠ CEF.∴∠ CEF = 20°.
在菱形中如果出现“30 °“”60 °“”120 °“”一边等于最短对角线”这些词语时,往往都指向等边三角形,我们需用等边三角形的知识来解决.
新知二 菱形的判定
1. 判定
图形 文字语言(判定) 符号语言
有一组邻边相等的平行四边形叫做菱形(定义法) ∵ AB=BC(或AB=AD 或AD=CD 或BC=CD)
∴ ABCD 是菱形
四边相等的四边形是菱形(判定1) ∵ AB=BC=AD=CD,
∴四边形ABCD 是菱形
对角线互相垂直的平行四边形是菱形(判定2) ∵ AC ⊥ BD.
∴ ABCD 是菱形
2. 易错警示 判定菱形时,一定要明确前提是从“四边形”出发的,还是从“平行四边形”出发的:(1)若从“四边形”出发,则还需四条边相等;(2)若从“平行四边形”出发,则还需一组邻边相等或对角线互相垂直.
特别提醒:
1.菱形的判定定理和性质定理是互逆定理.
2.判定菱形的常见思路
四
边
形
可依据题目特点选取不同的方法.
四条边都相等→菱形对角线互相垂直且平分→菱形
平行四边形
对角线互相垂直→菱形
有一组邻边相等→菱形
例2
已知:如图9.4.2-3,在△ ABC 中,CD 平分∠ ACB 交AB 于点D,DE ∥ AC 交BC 于点E,DF ∥ BC 交AC 于点F. 四边形DECF 是菱形吗?为什么?
解:四边形DECF 是菱形. 理由如下:
∵ DE ∥ FC,DF ∥ EC,
∴四边形DECF 为平行四边形.∵ AC ∥ DE,∴∠ 2= ∠ 3.
∵ CD 平分∠ ACB,∴∠ 1= ∠ 2. ∴∠ 1= ∠ 3.
∴ DE=EC.
∴平行四边形DECF 为菱形(有一组邻边相等的平行四边形是菱形).
解法提醒:
菱形的定义既是菱形的性质,也是菱形的一种判定方法.
在用菱形的定义判定一个四边形是菱形时,首先判定这个四边形是平行四边形,再证一组邻边相等.
平行
四边形
一组邻边相等
菱形
例 3
如图9.4.2-4,在平行四边形ABCD 中,对角线AC、BD 相交于点O,过点O 作直线EF ⊥ BD,分别交AD、BC 于点E 和点F,连接BE、DF. 求证:四边形BEDF 是菱形.
证明:∵四边形ABCD 是平行四边形,
∴ OB=OD,AD ∥ BC.
∴∠ EDO= ∠ FBO,∠ OED= ∠ OFB.
∴△ OED ≌△ OFB. ∴ DE=BF.
又∵ DE ∥ BF,∴四边形BEDF 是平行四边形.
∵ EF ⊥ BD,
∴平行四边形BEDF 是菱形(对角线互相垂直的平行四边形是菱形).
解法点拨:
证明一个四边形是菱形的方法:
若已知要证的四边形的对角线互相垂直,则要考虑证明这个四边形是平行四边形,用“对角线互相垂直的平行四边形是菱形”进行证明.
平行
四边形
对角线互
相垂直
菱形
例4
如图9.4.2-5,在Rt △ ACB 中,∠ ACB=90°,
∠ BAC=60°,DE 垂直平分BC,垂足为D,交AB 于点E,点F 在DE 的延长线上,且AF=CE. 求证:四边形ACEF 是菱形.
证明:∵ DE 垂直平分BC,∴ BE=CE.
∵∠ ACB=90° , ∠ BAC=60° ,
∴∠ BCE= ∠ B=30° . ∴∠ ACE=60° .
∴△ ACE 为等边三角形. ∴ AE=CE=AC.
∵∠ AEF= ∠ BED=90° - ∠ B=60°,AF=CE=AE,
∴△ AEF 为等边三角形.
∴ AE=AF=EF. ∴ AC=CE=EF=AF.
∴四边形ACEF 是菱形(四条边相等的四边形是菱形).
方法点拨:
有较多线段相等的条件时,我们可考虑通过证明四条边相等来证明这个四边形是菱形.注意:本例也可以先证四边形ACEF是平行四边形,再证一组邻边相等,只不过步骤复杂一点,读者不妨试一试.
如图,若要使 ABCD成为菱形,则需要添加的条件是( )
A.AB=CD
B.AD=AC
C.AB=BC
D.AC=BD
1
C
巩固新知
【2020·武威】如图所示的木制活动衣帽架由三个全等的菱形构成,根据实际需要可以调节A,E间的距离.若A,E间的距离调节到60 cm,菱形的边长AB=20 cm,则∠DAB的度数是( )
A.90°
B.100°
C.120°
D.150°
C
2
如图,菱形ABCD的周长是4 cm,∠ABC=60°,那么这个菱形的对角线AC的长是( )
A.1 cm
B.2 cm
C.3 cm
D.4 cm
3
A
【2021·河南】关于菱形的性质,以下说法不正确的是( )
A.四条边相等 B.对角线相等
C.对角线互相垂直 D.是轴对称图形
4
B
如图,菱形ABCD的对角线AC,BD相交于点O,过点D作DH⊥AB于点H,连接OH,若OA=6,OH=4,则菱形ABCD的面积为( )
A.72
B.24
C.48
D.96
5
C
6
D
7
B
【2021·广安】如图,四边形ABCD是菱形,点E,F分别在边AB,AD的延长线上,且BE=DF.连接CE,CF.
求证:CE=CF.
8
如图,在菱形ABCD中,点P是BC边上一点,连接AP,点E,F是AP上的两点,连接DE,BF,使得∠AED=∠ABC,∠ABF=∠BPF.
9
求证:(1)△ABF≌△DAE;
证明:∵四边形ABCD是菱形,
∴AB=AD,AD∥BC.∴∠BPA=∠DAE.
∵∠ABC=∠AED,∴∠BAF=∠ADE.
∵∠ABF=∠BPF,∴∠ABF=∠DAE.
∴△ABF≌△DAE(ASA).
(2)DE=BF+EF.
证明:∵△ABF≌△DAE,
∴BF=AE,AF=DE.
∴AF=AE+EF=BF+EF.∴DE=BF+EF.
菱形
菱形
边的性质
性质
角的性质
对角线的性质
定义
判定
边的关系
对称性
对角线关系
归纳新知
再见
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
