2021-2022学年苏科版数学八年级下册9.4.3正方形课件(30张)
文档属性
| 名称 | 2021-2022学年苏科版数学八年级下册9.4.3正方形课件(30张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-05 19:37:16 | ||
图片预览











文档简介
(共30张PPT)
9.4.3 正方形
第9章 中心对称图形——平行四边形
新知一 正方形的定义及其性质
1. 正方形的定义
有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.
合作探究
2. 正方形的性质如下表
图形 文字语言(性质) 符号语言
边 对边平行,四条边都相等 ∵四边形ABCD 是正方形,
∴ AB ∥ CD,AD ∥ BC,
AB=BC=CD=AD
角 四个角都是直角 ∵四边形ABCD 是正方形,∴∠ A= ∠ B= ∠ C= ∠ D=90°
图形 文字语言(性质) 符号语言
对角线 对角线互相垂直平分且相等 ∵四边形ABCD 是正方形,∴ AC ⊥ BD,AC=BD,OA=OC=OB=OD
对称性 既是轴对称图形,又是中心对称图形
3. 特别提醒 正方形具有四边形、平行四边形、矩形、菱形的一切性质.
特别提醒:
1.矩形、菱形、正方形都是特殊的平行
四边形,它们之间的关系如图9.4.3-1
所示.
2. 正方形的特殊性质:
(1)正方形的一条对角线把正方形分成两个全等的等腰直角三角形;两条对角线把正方形分成四个全等的小等腰直角三角形;
(2)周长相等的四边形中,正方形的面积最大;
(3)面积为边长的平方或对角线平方的一半.
例 1
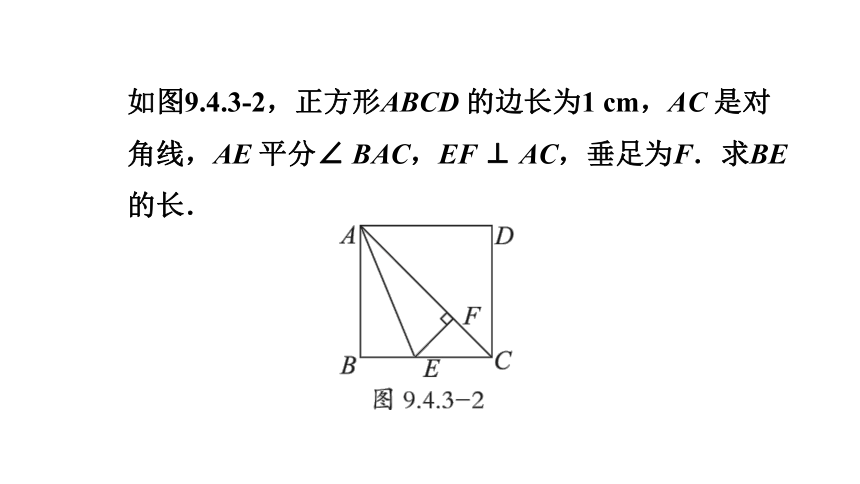
如图9.4.3-2,正方形ABCD 的边长为1 cm,AC 是对角线,AE 平分∠ BAC,EF ⊥ AC,垂足为F.求BE 的长.
解:∵四边形ABCD是边长为1cm的正方形,AC是对角线,
∴ AB ⊥ BC,AB = BC = 1 cm,∠ ACB = 45°.
∵ EF ⊥ AC,∴△ EFC是等腰直角三角形.
∴ FE = CF.
∵ AE 平分∠ BAC,EF ⊥ AC,∴ BE = FE = CF.
在Rt △ ABC 中,∠ ABC = 90°,
新知二 正方形的判定及特殊四边形间的关系
1. 正方形的判定如下表
图形 文字语言(判定) 符号语言
有一组邻边相等并且有一个角是直角的平行四边形叫做正方形(定义法) ∵ AB=BC(或AB=AD 或AD=CD 或BC=CD),
∠ A=90°(或∠ B=90°或∠ C=90 °或∠D=90 °),
∴ ABCD 是正方形
图形 文字语言(判定) 符号语言
有一组邻边相等的矩形是正方形(判定1) ∵ AB=BC(或AB=AD 或AD=CD或BC=CD),
∴矩形ABCD 是正方形
有一个角是直角的菱形是正方形(判定2) ∵∠ A=90°(或∠ B=90°或∠ C=90°或∠ D=90°),
∴菱形ABCD 是正方形
常见的判定思路:
(1)从四边形出发:①先证明四边形是平行四边形;②再证明平行四边形是正方形;
(2)从平行四边形出发:有一组邻边相等并且有一个角是直角的平行四边形是正方形;
(3)从矩形出发:有一组邻边相等的矩形是正方形;
(4)从菱形出发:有一个角是直角的菱形是正方形.
2. 特殊四边形间的关系
四边形、平行四边形、矩形、菱形、正方形间的转化关系如下所示.
例2
如图9.4.3-3,在Rt △ ABC 与Rt △ ABD 中,∠ABC=∠BAD=90°,AC=BD,AC、BD 相交于点G, 过点A 作AE ∥ DB 交CB 的延长线于点E, 过点B 作BF ∥ CA 交DA 的延长线于点F,AE、BF 相交于点H.
(1)证明:△ ABD ≌△ BAC;
证明:在Rt △ BAC 与Rt △ ABD 中,
∠ ABC =∠ BAD = 90°,
AB=BA,
AC=BD,
∴ Rt △ BAC ≌ Rt △ ABD.
(2)证明:四边形AHBG 是菱形;
证明:∵ AH ∥ GB,BH ∥ GA,
∴四边形AHBG 是平行四边形.
∵△ ABC ≌△ BAD,
∴∠ BAC =∠ ABD.∴ GA = GB.
∴平行四边形AHBG 是菱形(有一组邻边相等的平行四边形是菱形).
(3)若AB = BC,证明四边形AHBG 是正方形.
证明:∵ AB = BC,∠ ABC = 90°,
∴△ ABC 是等腰直角三角形.∴∠ BAG = 45°.
∴∠ ABG =∠ BAG = 45°.
∴∠AGB=90°.
∴菱形AHBG是正方形(有一个角是直角的菱形是正方形).
思路点拨:
(1)根据“HL”即可证明结论;
(2)先证明四边形AHBG是平行四边形,再由(1)中的全等易得GA = GB, 从而证明平行四边形AHBG 是菱形;
(3)根据“△ABC是等腰直角三角形”,得出∠BAG= 45°,再由(2)可知“∠ABG=∠BAG=45°”,根据三角形的内角和定理易得∠AGB=90°,最后根据判定2即可证明结论.
ABCD的对角线AC与BD相交于点O,且AC⊥BD,请添加一个条件:____________________,使得 ABCD为正方形.
1
AC=BD(答案不唯一)
巩固新知
【2021·无锡】下列说法中,正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.对角线相等的四边形是矩形
C.有一组邻边相等的矩形是正方形
D.对角线互相垂直的四边形是菱形
C
2
如图,四边形OBCD是正方形,O,D两点的坐标分别是(0,0),(0,6),点C在第一象限,则点C的坐标是( )
A.(6,3)
B.(3,6)
C.(0,6)
D.(6,6)
3
D
4
C
如图,在正方形ABCD中,点E,F分别在BC,CD上,BE=CF,则图中与∠AEB相等的角的个数是( )
A.1
B.2
C.3
D.4
5
C
下列命题是真命题的是( )
A.对角线相等的四边形是矩形
B.对角线互相垂直的四边形是矩形
C.对角线互相垂直的矩形是正方形
D.四边相等的平行四边形是正方形
6
C
【2021·玉林】如图,一个四边形顺次添加下列中的三个条件便得到正方形:
a.两组对边分别相等 b.一组对边平行且相等 c.一组邻边相等 d.一个角是直角
顺次添加的条件:①a→c→d;②b→d→c;③a→b→c,则正确的是( )
A.仅① B.仅③
C.①② D.②③
7
C
【2021·恩施州】如图,正方形ABCD的边长为4,点E在AB上且BE=1,F为对角线AC上一动点,则△BFE周长的最小值为( )
A.5
B.6
C.7
D.8
8
B
如图,在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证:△BED≌△CFD;
9
证明:∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.
∵AB=AC,∴∠B=∠C.
∵D是BC的中点,∴BD=CD.
∴△BED≌△CFD.
(2)若∠A=90°,求证:四边形DFAE是正方形.
证明:∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°.
又∵∠A=90°,∴四边形DFAE为矩形.
由(1)知,△BED≌△CFD,
∴DE=DF.
∴四边形DFAE是正方形.
正方形
正
方
形
性质
判定
特殊的平行四边形
特殊的矩形
特殊的菱形
边、角、对角线、对称性
一组邻边相等
且一个角是直角
一组邻边相等
一个角是直角
归纳新知
再见
9.4.3 正方形
第9章 中心对称图形——平行四边形
新知一 正方形的定义及其性质
1. 正方形的定义
有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.
合作探究
2. 正方形的性质如下表
图形 文字语言(性质) 符号语言
边 对边平行,四条边都相等 ∵四边形ABCD 是正方形,
∴ AB ∥ CD,AD ∥ BC,
AB=BC=CD=AD
角 四个角都是直角 ∵四边形ABCD 是正方形,∴∠ A= ∠ B= ∠ C= ∠ D=90°
图形 文字语言(性质) 符号语言
对角线 对角线互相垂直平分且相等 ∵四边形ABCD 是正方形,∴ AC ⊥ BD,AC=BD,OA=OC=OB=OD
对称性 既是轴对称图形,又是中心对称图形
3. 特别提醒 正方形具有四边形、平行四边形、矩形、菱形的一切性质.
特别提醒:
1.矩形、菱形、正方形都是特殊的平行
四边形,它们之间的关系如图9.4.3-1
所示.
2. 正方形的特殊性质:
(1)正方形的一条对角线把正方形分成两个全等的等腰直角三角形;两条对角线把正方形分成四个全等的小等腰直角三角形;
(2)周长相等的四边形中,正方形的面积最大;
(3)面积为边长的平方或对角线平方的一半.
例 1
如图9.4.3-2,正方形ABCD 的边长为1 cm,AC 是对角线,AE 平分∠ BAC,EF ⊥ AC,垂足为F.求BE 的长.
解:∵四边形ABCD是边长为1cm的正方形,AC是对角线,
∴ AB ⊥ BC,AB = BC = 1 cm,∠ ACB = 45°.
∵ EF ⊥ AC,∴△ EFC是等腰直角三角形.
∴ FE = CF.
∵ AE 平分∠ BAC,EF ⊥ AC,∴ BE = FE = CF.
在Rt △ ABC 中,∠ ABC = 90°,
新知二 正方形的判定及特殊四边形间的关系
1. 正方形的判定如下表
图形 文字语言(判定) 符号语言
有一组邻边相等并且有一个角是直角的平行四边形叫做正方形(定义法) ∵ AB=BC(或AB=AD 或AD=CD 或BC=CD),
∠ A=90°(或∠ B=90°或∠ C=90 °或∠D=90 °),
∴ ABCD 是正方形
图形 文字语言(判定) 符号语言
有一组邻边相等的矩形是正方形(判定1) ∵ AB=BC(或AB=AD 或AD=CD或BC=CD),
∴矩形ABCD 是正方形
有一个角是直角的菱形是正方形(判定2) ∵∠ A=90°(或∠ B=90°或∠ C=90°或∠ D=90°),
∴菱形ABCD 是正方形
常见的判定思路:
(1)从四边形出发:①先证明四边形是平行四边形;②再证明平行四边形是正方形;
(2)从平行四边形出发:有一组邻边相等并且有一个角是直角的平行四边形是正方形;
(3)从矩形出发:有一组邻边相等的矩形是正方形;
(4)从菱形出发:有一个角是直角的菱形是正方形.
2. 特殊四边形间的关系
四边形、平行四边形、矩形、菱形、正方形间的转化关系如下所示.
例2
如图9.4.3-3,在Rt △ ABC 与Rt △ ABD 中,∠ABC=∠BAD=90°,AC=BD,AC、BD 相交于点G, 过点A 作AE ∥ DB 交CB 的延长线于点E, 过点B 作BF ∥ CA 交DA 的延长线于点F,AE、BF 相交于点H.
(1)证明:△ ABD ≌△ BAC;
证明:在Rt △ BAC 与Rt △ ABD 中,
∠ ABC =∠ BAD = 90°,
AB=BA,
AC=BD,
∴ Rt △ BAC ≌ Rt △ ABD.
(2)证明:四边形AHBG 是菱形;
证明:∵ AH ∥ GB,BH ∥ GA,
∴四边形AHBG 是平行四边形.
∵△ ABC ≌△ BAD,
∴∠ BAC =∠ ABD.∴ GA = GB.
∴平行四边形AHBG 是菱形(有一组邻边相等的平行四边形是菱形).
(3)若AB = BC,证明四边形AHBG 是正方形.
证明:∵ AB = BC,∠ ABC = 90°,
∴△ ABC 是等腰直角三角形.∴∠ BAG = 45°.
∴∠ ABG =∠ BAG = 45°.
∴∠AGB=90°.
∴菱形AHBG是正方形(有一个角是直角的菱形是正方形).
思路点拨:
(1)根据“HL”即可证明结论;
(2)先证明四边形AHBG是平行四边形,再由(1)中的全等易得GA = GB, 从而证明平行四边形AHBG 是菱形;
(3)根据“△ABC是等腰直角三角形”,得出∠BAG= 45°,再由(2)可知“∠ABG=∠BAG=45°”,根据三角形的内角和定理易得∠AGB=90°,最后根据判定2即可证明结论.
ABCD的对角线AC与BD相交于点O,且AC⊥BD,请添加一个条件:____________________,使得 ABCD为正方形.
1
AC=BD(答案不唯一)
巩固新知
【2021·无锡】下列说法中,正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.对角线相等的四边形是矩形
C.有一组邻边相等的矩形是正方形
D.对角线互相垂直的四边形是菱形
C
2
如图,四边形OBCD是正方形,O,D两点的坐标分别是(0,0),(0,6),点C在第一象限,则点C的坐标是( )
A.(6,3)
B.(3,6)
C.(0,6)
D.(6,6)
3
D
4
C
如图,在正方形ABCD中,点E,F分别在BC,CD上,BE=CF,则图中与∠AEB相等的角的个数是( )
A.1
B.2
C.3
D.4
5
C
下列命题是真命题的是( )
A.对角线相等的四边形是矩形
B.对角线互相垂直的四边形是矩形
C.对角线互相垂直的矩形是正方形
D.四边相等的平行四边形是正方形
6
C
【2021·玉林】如图,一个四边形顺次添加下列中的三个条件便得到正方形:
a.两组对边分别相等 b.一组对边平行且相等 c.一组邻边相等 d.一个角是直角
顺次添加的条件:①a→c→d;②b→d→c;③a→b→c,则正确的是( )
A.仅① B.仅③
C.①② D.②③
7
C
【2021·恩施州】如图,正方形ABCD的边长为4,点E在AB上且BE=1,F为对角线AC上一动点,则△BFE周长的最小值为( )
A.5
B.6
C.7
D.8
8
B
如图,在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证:△BED≌△CFD;
9
证明:∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.
∵AB=AC,∴∠B=∠C.
∵D是BC的中点,∴BD=CD.
∴△BED≌△CFD.
(2)若∠A=90°,求证:四边形DFAE是正方形.
证明:∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°.
又∵∠A=90°,∴四边形DFAE为矩形.
由(1)知,△BED≌△CFD,
∴DE=DF.
∴四边形DFAE是正方形.
正方形
正
方
形
性质
判定
特殊的平行四边形
特殊的矩形
特殊的菱形
边、角、对角线、对称性
一组邻边相等
且一个角是直角
一组邻边相等
一个角是直角
归纳新知
再见
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
