2021—2022学年人教版数学八年级下册第19章一次函数复习课件(32张)
文档属性
| 名称 | 2021—2022学年人教版数学八年级下册第19章一次函数复习课件(32张) |  | |
| 格式 | zip | ||
| 文件大小 | 844.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-05 19:39:08 | ||
图片预览










文档简介
(共32张PPT)
一次函数
目录
01
教学目标
02
知识点框架
03
例题练习
04
作业布置
教学目标
01
教学目标
1.理解函数的定义及表示法,能求简单问题中的函数关系及自变量的取值范围;
2.理解一次函数及正比例函数的定义;
3.会画一次函数的图象,并能结合一次函数的图象和解析式说出其性质;
4.能根据具体情境确定一次函数的解析式
5.体会一次函数与一次方程(组)、一元一次不等式之间的联系,并能解决简单问题;
6.能从具体问题情境中抽象出一次函数的模型,并能解决简单的实际问题.
知识点框架
02
知识点框架
一、变量与函数
1、在一个变化过程中,数值发生变化的量为 ,数值始终不变的量为 。
2、一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是 ,y是x的 。如果当x=a时y=b,那么b叫做当自变量的值为a时的 。
3、用关于自变量的数学式子表示函数与自变量之间的关系,这种式子叫做函数的 。
4、函数的图象:对于一个函数,如果把自变量与函数的每对对应值分别作为点的横坐标和纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象。
5、描点法画函数图象的步骤: 、 、 。
6、函数的表示方法: , , 。
知识点框架
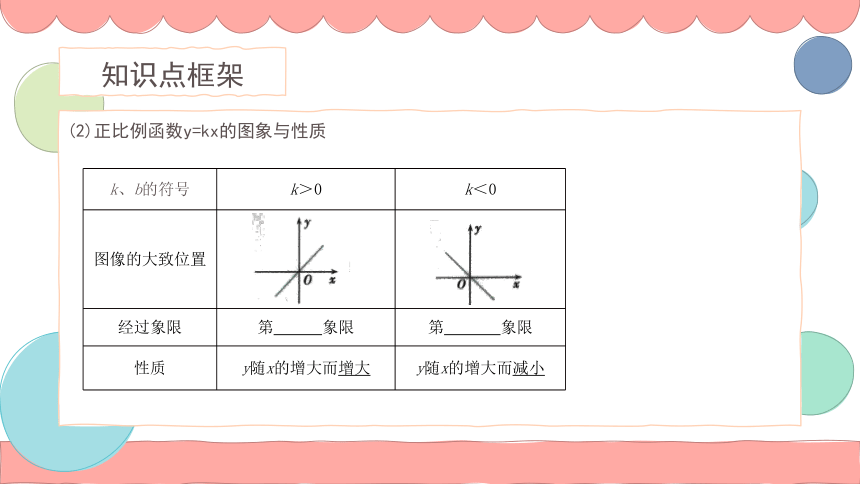
(2)正比例函数y=kx的图象与性质
k、b的符号 k>0 k<0
图像的大致位置
经过象限 第 象限 第 象限
性质 y随x的增大而增大 y随x的增大而减小
知识点框架
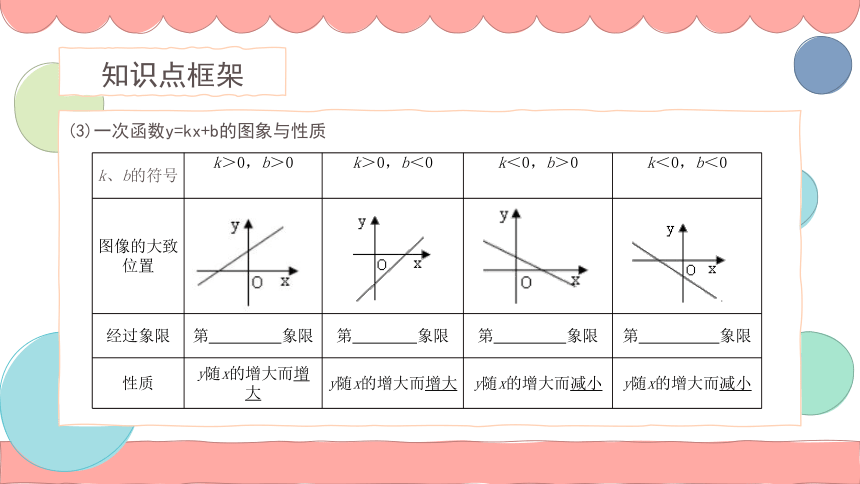
(3)一次函数y=kx+b的图象与性质
k、b的符号 k>0,b>0 k>0,b<0 k<0,b>0 k<0,b<0
图像的大致位置
经过象限 第 象限 第 象限 第 象限 第 象限
性质 y随x的增大而增大 y随x的增大而增大 y随x的增大而减小 y随x的增大而减小
知识点框架
(4)一次函数图象的平移
比较一次函数y=kx+b(k≠0)与正比例函数y=kx(k≠0)的解析式,容易得出:一次函数y=kx+b(k≠0)的图象可以由直线y=kx(k≠0)平移|b|个单位长度得到,当b>0时,向上平移,当b<0时,向下平移
3.用待定系数法求函数解析式
常用待定系数法求一次函数的解析式,待定系数法的一般步骤是:
(1)设出函数解析式;
(2)根据已知条件列出关于待定系数的方程或方程组;
(3)求出k、b的值;
(4)写出这个解析式.
知识点框架
4.一次函数与方程、方程组及不等式的关系
(1)y=kx+b与kx+b=0
直线y=kx+b与x轴交点的横坐标是方程kx+b=0的解,方程kx+b=0的解是直线y=kx+b与x轴交点的横坐标.
(2)一次函数与方程组
两个一次函数图象的交点坐标就是它们的解析式所组成的二元一次方程组的解;以二元一次方程组的解为坐标的点是两个二元一次方程所对应的一次函数图象的交点.
(3)y=kx+b与不等式kx+b>0
从函数值的角度看,不等式kx+b>0的解集为使函数值大于零(即kx+b>0)的x的取值范围;从图象的角度看,由于一次函数的图象在x轴上方时,y>0,因此kx+b>0的解集为一次函数在x轴上方的图象所对应的x的取值范围.类似可知y=kx+b与不等式kx+b<0的关系.
例题练习
03
例题
例5.一次函数y=-0.5x+1的图像不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
例6.一次函数y=-2x+4的图象与y轴的交点坐标是( )
A.(0,4) B.(4,0) C.(2,0) D.(0,2)
例7.直线y=(2-5k)x+3k-2若经过原点,则k= 。
例8.如图一次函数y=kx+b的图象与正比例函数y=2x的图象平行
且经过点A(1,-2),则kb=________.
例题
例9.正比例函数的图像如图,则这个函数的解析式为( )
A.y=x B.y=-2x C.y=-x D.
例10.直线AB与x轴交于点A(-,0),与y轴交于点B(0,1),求直线AB的解析式;
例11. 一次函数y=kx+b(k、b为常数,且k≠0)的图象如图所示.根据图象
信息可求得关于x的方程kx+b=0的解为______________.
练习
4.当自变量x增大时,下列函数值反而减小的是( )
A.y= B.y=2x C.y= D.y=-2+5x
5.直线y=(2-5k)x+3k-2不过第一象限,则k需满足 ,写出一个满足上述条件的一个函数的解析式 .
6.已知关于x的一次函数y=(2k-3)x+k-1的图像与y轴交点在x轴的上方,且y随x的增大而减小,求k的取值范围;
练习
7.根据所给函数图象,写出函数关系式
8.在坐标平面上,若点(3, b)在方程3y=2x-9的图象上,则b的值为( )
A.-1 B.2 C.3 D.9
总结
一次函数
作业布置
04
作业布置
1.一次函数y=2x+1的图像不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.关于一次函数y=2x﹣1的图象,下列说法正确的是( )
A.图象经过第一、二、三象限 B.图象经过第一、三、四象限
C.图象经过第一、二、四象限 D.图象经过第二、三、四象限
3.函数y=x﹣2的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
作业布置
8.一次函数y=mx+∣m-1∣的图象过点(0,2)且y随x的增大而增大,则m=( )
A.-1 B.3 C.1 D.-1或3
9.同一温度的华氏度数y(℉)与摄氏度数x(℃)之间的函数关系是y= x+32.如果某一温度的摄氏度数是25℃,那么它的华氏度数是________℉.
10.把直线y=-x-1沿x轴向右平移2个单位,所得直线的函数解析式为 .
11.直线y=-3x+5不经过的象限为 .
12.已知直线y=2x+(3-a)与x轴的交点在A(2,0),B(3,0)之间(包括A、B两点)则a的取值范围是 .
作业布置
13.一次函数y=2x﹣6的图象与x轴的交点坐标为 .
14.已知关于x的一次函数y=kx+4k﹣2(k≠0).若其图象经过原点,则k= ,若y随着x的增大而减小,则k的取值范围是 .
15.已知一次函数y=kx+3的图象经过点(1,4).
(1)求这个一次函数的解析式.
(2)求关于x的不等式kx+3≤6的解集
下节课见!
一次函数
目录
01
教学目标
02
知识点框架
03
例题练习
04
作业布置
教学目标
01
教学目标
1.理解函数的定义及表示法,能求简单问题中的函数关系及自变量的取值范围;
2.理解一次函数及正比例函数的定义;
3.会画一次函数的图象,并能结合一次函数的图象和解析式说出其性质;
4.能根据具体情境确定一次函数的解析式
5.体会一次函数与一次方程(组)、一元一次不等式之间的联系,并能解决简单问题;
6.能从具体问题情境中抽象出一次函数的模型,并能解决简单的实际问题.
知识点框架
02
知识点框架
一、变量与函数
1、在一个变化过程中,数值发生变化的量为 ,数值始终不变的量为 。
2、一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是 ,y是x的 。如果当x=a时y=b,那么b叫做当自变量的值为a时的 。
3、用关于自变量的数学式子表示函数与自变量之间的关系,这种式子叫做函数的 。
4、函数的图象:对于一个函数,如果把自变量与函数的每对对应值分别作为点的横坐标和纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象。
5、描点法画函数图象的步骤: 、 、 。
6、函数的表示方法: , , 。
知识点框架
(2)正比例函数y=kx的图象与性质
k、b的符号 k>0 k<0
图像的大致位置
经过象限 第 象限 第 象限
性质 y随x的增大而增大 y随x的增大而减小
知识点框架
(3)一次函数y=kx+b的图象与性质
k、b的符号 k>0,b>0 k>0,b<0 k<0,b>0 k<0,b<0
图像的大致位置
经过象限 第 象限 第 象限 第 象限 第 象限
性质 y随x的增大而增大 y随x的增大而增大 y随x的增大而减小 y随x的增大而减小
知识点框架
(4)一次函数图象的平移
比较一次函数y=kx+b(k≠0)与正比例函数y=kx(k≠0)的解析式,容易得出:一次函数y=kx+b(k≠0)的图象可以由直线y=kx(k≠0)平移|b|个单位长度得到,当b>0时,向上平移,当b<0时,向下平移
3.用待定系数法求函数解析式
常用待定系数法求一次函数的解析式,待定系数法的一般步骤是:
(1)设出函数解析式;
(2)根据已知条件列出关于待定系数的方程或方程组;
(3)求出k、b的值;
(4)写出这个解析式.
知识点框架
4.一次函数与方程、方程组及不等式的关系
(1)y=kx+b与kx+b=0
直线y=kx+b与x轴交点的横坐标是方程kx+b=0的解,方程kx+b=0的解是直线y=kx+b与x轴交点的横坐标.
(2)一次函数与方程组
两个一次函数图象的交点坐标就是它们的解析式所组成的二元一次方程组的解;以二元一次方程组的解为坐标的点是两个二元一次方程所对应的一次函数图象的交点.
(3)y=kx+b与不等式kx+b>0
从函数值的角度看,不等式kx+b>0的解集为使函数值大于零(即kx+b>0)的x的取值范围;从图象的角度看,由于一次函数的图象在x轴上方时,y>0,因此kx+b>0的解集为一次函数在x轴上方的图象所对应的x的取值范围.类似可知y=kx+b与不等式kx+b<0的关系.
例题练习
03
例题
例5.一次函数y=-0.5x+1的图像不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
例6.一次函数y=-2x+4的图象与y轴的交点坐标是( )
A.(0,4) B.(4,0) C.(2,0) D.(0,2)
例7.直线y=(2-5k)x+3k-2若经过原点,则k= 。
例8.如图一次函数y=kx+b的图象与正比例函数y=2x的图象平行
且经过点A(1,-2),则kb=________.
例题
例9.正比例函数的图像如图,则这个函数的解析式为( )
A.y=x B.y=-2x C.y=-x D.
例10.直线AB与x轴交于点A(-,0),与y轴交于点B(0,1),求直线AB的解析式;
例11. 一次函数y=kx+b(k、b为常数,且k≠0)的图象如图所示.根据图象
信息可求得关于x的方程kx+b=0的解为______________.
练习
4.当自变量x增大时,下列函数值反而减小的是( )
A.y= B.y=2x C.y= D.y=-2+5x
5.直线y=(2-5k)x+3k-2不过第一象限,则k需满足 ,写出一个满足上述条件的一个函数的解析式 .
6.已知关于x的一次函数y=(2k-3)x+k-1的图像与y轴交点在x轴的上方,且y随x的增大而减小,求k的取值范围;
练习
7.根据所给函数图象,写出函数关系式
8.在坐标平面上,若点(3, b)在方程3y=2x-9的图象上,则b的值为( )
A.-1 B.2 C.3 D.9
总结
一次函数
作业布置
04
作业布置
1.一次函数y=2x+1的图像不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.关于一次函数y=2x﹣1的图象,下列说法正确的是( )
A.图象经过第一、二、三象限 B.图象经过第一、三、四象限
C.图象经过第一、二、四象限 D.图象经过第二、三、四象限
3.函数y=x﹣2的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
作业布置
8.一次函数y=mx+∣m-1∣的图象过点(0,2)且y随x的增大而增大,则m=( )
A.-1 B.3 C.1 D.-1或3
9.同一温度的华氏度数y(℉)与摄氏度数x(℃)之间的函数关系是y= x+32.如果某一温度的摄氏度数是25℃,那么它的华氏度数是________℉.
10.把直线y=-x-1沿x轴向右平移2个单位,所得直线的函数解析式为 .
11.直线y=-3x+5不经过的象限为 .
12.已知直线y=2x+(3-a)与x轴的交点在A(2,0),B(3,0)之间(包括A、B两点)则a的取值范围是 .
作业布置
13.一次函数y=2x﹣6的图象与x轴的交点坐标为 .
14.已知关于x的一次函数y=kx+4k﹣2(k≠0).若其图象经过原点,则k= ,若y随着x的增大而减小,则k的取值范围是 .
15.已知一次函数y=kx+3的图象经过点(1,4).
(1)求这个一次函数的解析式.
(2)求关于x的不等式kx+3≤6的解集
下节课见!
