2021-2022学年鲁教版(五四制)七年级数学上册第5章位置与坐标 期末综合复习训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)七年级数学上册第5章位置与坐标 期末综合复习训练(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 154.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-05 20:33:32 | ||
图片预览


文档简介
2021-2022学年鲁教版七年级数学上册《第5章位置与坐标》期末综合复习训练(附答案)
1.平面直角坐标系中,点A(﹣3,5)关于x轴对称的点的坐标为( )
A.(﹣3,5) B.(﹣3,﹣5) C.(3,﹣5) D.(3,5)
2.已知点A(m+2,3)与点B(﹣4,n+5)关于y轴对称,则m+n的值为( )
A.﹣8 B.0 C.﹣6 D.﹣14
3.在平面直角坐标系中,下列各点中到x轴的距离是4,且在第四象限的是( )
A.(4,﹣5) B.(﹣4,5) C.(﹣5,4) D.(5,﹣4)
4.在平面直角坐标系中,把点A(﹣1,﹣3)先向右平移2个单位,再向上平移3个单位,所得点的坐标是( )
A.(﹣3,0) B.(1,0) C.(﹣3,﹣6) D.(1,﹣6)
5.如图是棋盘的一部分,建立适当的平面直角坐标系,已知棋子“车”的坐标为(﹣2,1),棋子“马”的坐标为(3,﹣1),则棋子“炮”的坐标为( )
A.(1,1) B.(2,1) C.(2,2) D.(3,1)
6.已知点A(4,2),B(﹣2,2),则直线AB( )
A.平行于x轴 B.平行于y轴
C.经过原点 D.以上都有可能
7.在平面直角坐标系中,已知点A的坐标是(3,a),将点A向下平移4个单位得到点A'.若点A与点A'关于x轴对称,则a的值为( )
A.﹣2 B.2 C.﹣1 D.1
8.在平面直角坐标系中,下列说法正确的是( )
A.点P(3,2)到x轴的距离是3
B.若ab=0,则点P(a,b)表示原点
C.若A(2,﹣2)、B(2,2),则直线AB∥x轴
D.第三象限内点的坐标,横纵坐标同号
9.已知在平面直角坐标系中,点P在第二象限且点P到x轴和y轴的距离分别6和5,那么点P的坐标为( )
A.(﹣5,﹣6) B.(﹣6,﹣5) C.(﹣5,6) D.(﹣6,5)
10.已知点A的坐标为(a+1,3﹣a),下列说法正确的是( )
A.若点A在y轴上,则a=3 B.若点A在一三象限角平分线上,则a=1
C.若点A到x轴的距离是3,则a=±6 D.若点A在第四象限,则a的值可以为﹣2
11.平面直角坐标系中,点A(﹣3,2),B(3,4),C(x,y),若AC∥x轴,则线段BC的最小值及此时点C的坐标分别为( )
A.6,(﹣3,4) B.2,(3,2) C.2,(3,0) D.1,(4,2)
12.已知点P(1,y),Q(x,2),若PQ∥x轴,且线段PQ=3,则x= ,y= .
13.已知点(a+1,2a+5)在y轴上,则该点坐标为 .
14.已知线段AB=4,AB∥x轴,若点A坐标为(﹣1,2),且点B在第一象限,则B点坐标为 .
15.在平面直角坐标系中,点A(﹣5,4)到y轴的距离是 ,点A关于x轴的对称点A′的坐标为 .
16.点P是第一象限内的点,若点P(2+a,3a+4)到x轴和y轴的距离相等,则点P的坐标为 .
17.若把点A(5m,2m﹣1)向上平移3个单位长度后,得到的点在x轴上,则点A的坐标为 .
18.已知平面直角坐标系中有一点M(m﹣1,2m+3)
(1)当m为何值时,点M到x轴的距离为1?
(2)当m为何值时,点M到y轴的距离为2?
19.如图,A(﹣1,0),C(1,4),点B在x轴上,且AB=3.
(1)求点B的坐标;
(2)求△ABC的面积;
(3)在y轴上是否存在点P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请直接写出点P的坐标;若不存在,请说明理由.
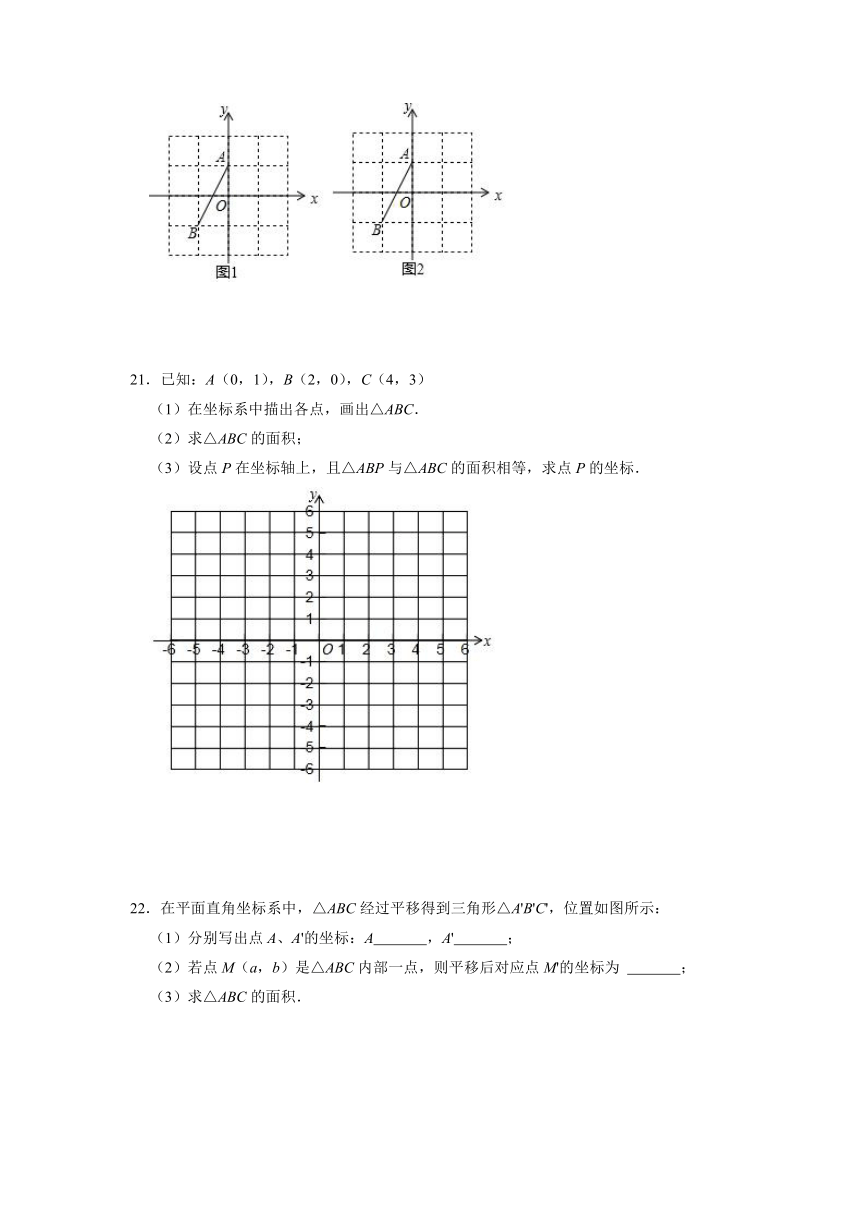
20.在4×4的正方形网格中建立如图1、2所示的直角坐标系,其中格点A,B的坐标分别是(0,1),(﹣1,﹣1).(1)请图1中添加一个格点C,使得△ABC是轴对称图形,且对称轴经过点(0,﹣1).
(2)请图2中添加一个格点D,使得△ABD也是轴对称图形,且对称轴经过点(1,1).
21.已知:A(0,1),B(2,0),C(4,3)
(1)在坐标系中描出各点,画出△ABC.
(2)求△ABC的面积;
(3)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.
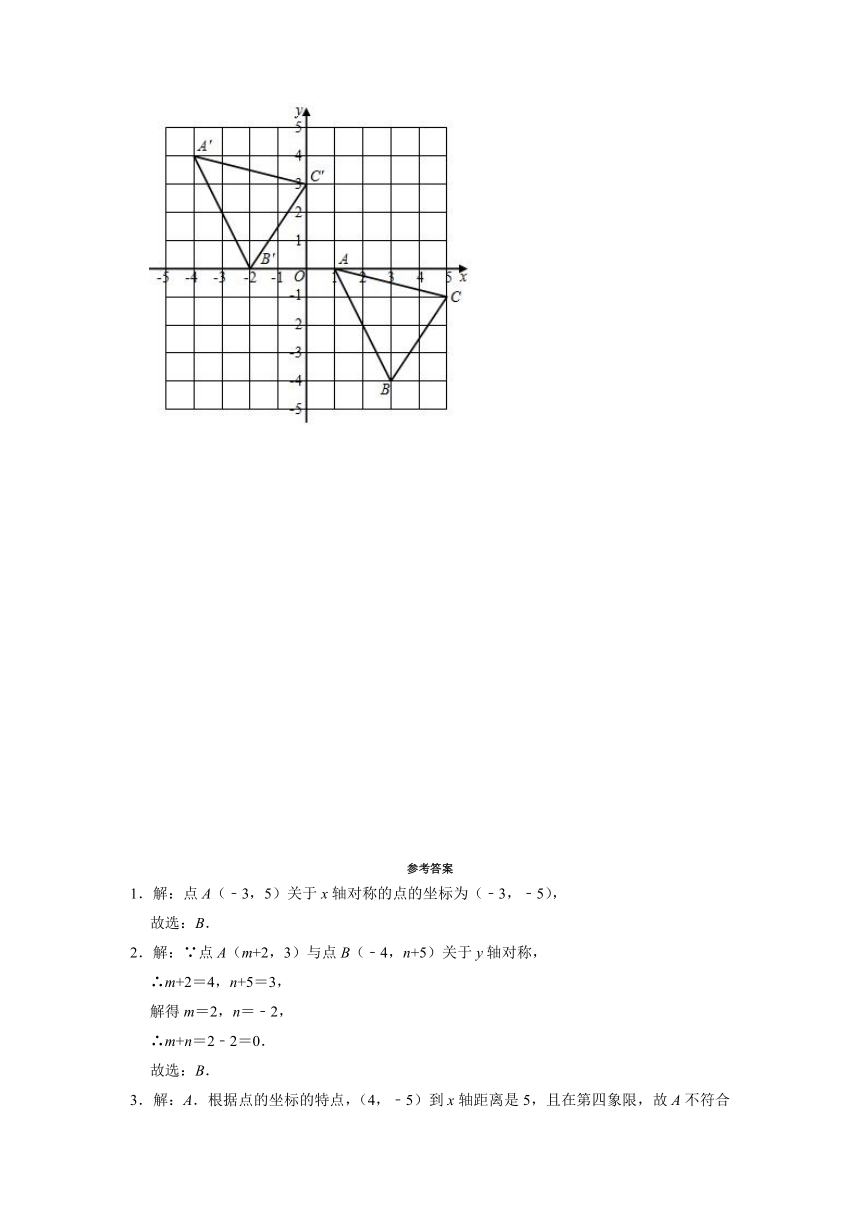
22.在平面直角坐标系中,△ABC经过平移得到三角形△A'B'C',位置如图所示:
(1)分别写出点A、A'的坐标:A ,A' ;
(2)若点M(a,b)是△ABC内部一点,则平移后对应点M'的坐标为 ;
(3)求△ABC的面积.
参考答案
1.解:点A(﹣3,5)关于x轴对称的点的坐标为(﹣3,﹣5),
故选:B.
2.解:∵点A(m+2,3)与点B(﹣4,n+5)关于y轴对称,
∴m+2=4,n+5=3,
解得m=2,n=﹣2,
∴m+n=2﹣2=0.
故选:B.
3.解:A.根据点的坐标的特点,(4,﹣5)到x轴距离是5,且在第四象限,故A不符合题意.
B.根据点的坐标的特点,(﹣4,5)到x轴距离是5,且在第二象限,故B不符合题意.
C.根据点的坐标的特点,(﹣5,4)到x轴距离是4,且在第二象限,故C不符合题意.
D.根据点的坐标的特点,(5,﹣4)到x轴距离是4,且在第四象限,故D符合题意.
故选:D.
4.解:平移后点A的坐标为(﹣1+2,﹣3+3),即A(1,0),
故选:B.
5.解:根据题意可建立如图所示的平面直角坐标系:
则棋子“炮”的坐标为(2,1),
故选:B.
6.解:∵A(4,2),B(﹣2,2),
∴点A到x轴的距离为2,点B到x轴的距离为2,且A、B都在x轴上方,
∴AB平行于x轴,
故选:A.
7.解:∵点A的坐标是(3,a),将点A向下平移4个单位得到点A',
∴A'的坐标为(3,a﹣4),
∵点A与点A'关于x轴对称,
∴a+a﹣4=0,
解得:a=2.
故选:B.
8.解:A、点P(3,2)到x轴的距离是2,故本选项不符合题意.
B、若ab=0,则点P(a,b)表示原点或坐标轴上的点,故本选项不符合题意.
C、若A(2,﹣2)、B(2,2),则直线AB∥y轴,故本选项不符合题意.
D、第三象限内点的坐标,横纵坐标都是负号,故本选项符合题意.
故选:D.
9.解:第二象限内的点横坐标小于0,纵坐标大于0;
到x轴的距离是6,说明其纵坐标为6,到y轴的距离为5,说明其横坐标为﹣5,
因而点P的坐标是(﹣5,6).
故选:C.
10.解:A.若点A在y轴上,则a+1=0,解得a=﹣1,故本选项错误;
B.若点A在一三象限角平分线上,则a+1=3﹣a,解得a=1,故本选项正确;
C.若点A到x轴的距离是3,则|3﹣a|=3,解得a=6或0,故本选项错误;
D.若点A在第四象限,则a+1>0,且3﹣a<0,解得a>3,故a的值不可以为﹣2;
故选:B.
11.解:如图所示:
由垂线段最短可知:当BC⊥AC时,BC有最小值.
∴点C的坐标为(3,2),线段的最小值为2.
故选:B.
12.解:∵P(1,y),Q(x,2),且PQ∥x轴,
∴y=2,
又∵PQ=3,
∴|x﹣1|=3
∴x=4或﹣2,
故答案为:4或﹣2,2.
13.解:∵点(a+1,2a+5)在y轴上,
∴a+1=0,
解得:a=﹣1,
∴2a+5=3,
∴该点坐标为:(0,3).
故答案为:(0,3).
14.解:∵AB∥x轴,点A坐标为(﹣1,2),
∴A、B两点纵坐标都为2,
又∵AB=4,且点B在第一象限,点A坐标为(﹣1,2),
∴B点在A点右边,B(3,2).
故答案为:(3,2).
15.解:根据坐标的定义可知,
点A(﹣5,4)到y轴的距离是|﹣5|=5,
由关于x轴的对称点坐标之间的关系可得,
点A关于x轴的对称点A′的坐标为(﹣5,﹣4),
故答案为:5,(﹣5,﹣4).
16.解:∵点P是第一象限内的点,点P(2+a,3a+4)到x轴和y轴的距离相等,
∴2+a=3a+4,
解得a=﹣1,
∴点P的坐标为(1,1),
故答案为(1,1).
17.解:∵把点A(5m,2m﹣1)向上平移3个单位后得到的点在x轴上,
∴2m﹣1+3=0,
解得m=﹣1,
∴点A坐标为(﹣5,﹣3),
故答案为:(﹣5,﹣3).
18.解:(1)∵|2m+3|=1
2m+3=1或2m+3=﹣1
∴m=﹣1或m=﹣2;
(2)∵|m﹣1|=2
m﹣1=2或m﹣1=﹣2
∴m=3或m=﹣1.
19.解:(1)点B在点A的右边时,﹣1+3=2,
点B在点A的左边时,﹣1﹣3=﹣4,
所以,B的坐标为(2,0)或(﹣4,0);
(2)△ABC的面积=×3×4=6;
(3)设点P到x轴的距离为h,
则×3h=10,
解得h=,
点P在y轴正半轴时,P(0,),
点P在y轴负半轴时,P(0,﹣),
综上所述,点P的坐标为(0,)或(0,﹣).
20.解:(1)如图,点C即为所求.
(2)如图,点D即为所求.
21.解:(1)如图所示:
(2)过点C向x、y轴作垂线,垂足为D、E.
∴四边形DOEC的面积=3×4=12,△BCD的面积==3,△ACE的面积==4,△AOB的面积==1.
∴△ABC的面积=四边形DOEC的面积﹣△ACE的面积﹣△BCD的面积﹣△AOB的面积
=12﹣3﹣4﹣1=4.
(3)当点p在x轴上时,△ABP的面积==4,即:,解得:BP=8,
所以点P的坐标为(10,0)或(﹣6,0);
当点P在y轴上时,△ABP的面积==4,即,解得:AP=4.
所以点P的坐标为(0,5)或(0,﹣3).
所以点P的坐标为(0,5)或(0,﹣3)或(10,0)或(﹣6,0).
22.解:(1)观察图象可知,A(1,0),A′(﹣4,4),
故答案为:(1,0),(﹣4,4);
(2)∵△ABC向左平移5个单位,向上平移4个单位得到△A′B′C′.
∴M(a,b),平移后的坐标为(a﹣5,b+4),
故答案为:(a﹣5,b+4);
(3)S△ABC=4×4﹣×2×4﹣×1×4﹣×2×3=7.
1.平面直角坐标系中,点A(﹣3,5)关于x轴对称的点的坐标为( )
A.(﹣3,5) B.(﹣3,﹣5) C.(3,﹣5) D.(3,5)
2.已知点A(m+2,3)与点B(﹣4,n+5)关于y轴对称,则m+n的值为( )
A.﹣8 B.0 C.﹣6 D.﹣14
3.在平面直角坐标系中,下列各点中到x轴的距离是4,且在第四象限的是( )
A.(4,﹣5) B.(﹣4,5) C.(﹣5,4) D.(5,﹣4)
4.在平面直角坐标系中,把点A(﹣1,﹣3)先向右平移2个单位,再向上平移3个单位,所得点的坐标是( )
A.(﹣3,0) B.(1,0) C.(﹣3,﹣6) D.(1,﹣6)
5.如图是棋盘的一部分,建立适当的平面直角坐标系,已知棋子“车”的坐标为(﹣2,1),棋子“马”的坐标为(3,﹣1),则棋子“炮”的坐标为( )
A.(1,1) B.(2,1) C.(2,2) D.(3,1)
6.已知点A(4,2),B(﹣2,2),则直线AB( )
A.平行于x轴 B.平行于y轴
C.经过原点 D.以上都有可能
7.在平面直角坐标系中,已知点A的坐标是(3,a),将点A向下平移4个单位得到点A'.若点A与点A'关于x轴对称,则a的值为( )
A.﹣2 B.2 C.﹣1 D.1
8.在平面直角坐标系中,下列说法正确的是( )
A.点P(3,2)到x轴的距离是3
B.若ab=0,则点P(a,b)表示原点
C.若A(2,﹣2)、B(2,2),则直线AB∥x轴
D.第三象限内点的坐标,横纵坐标同号
9.已知在平面直角坐标系中,点P在第二象限且点P到x轴和y轴的距离分别6和5,那么点P的坐标为( )
A.(﹣5,﹣6) B.(﹣6,﹣5) C.(﹣5,6) D.(﹣6,5)
10.已知点A的坐标为(a+1,3﹣a),下列说法正确的是( )
A.若点A在y轴上,则a=3 B.若点A在一三象限角平分线上,则a=1
C.若点A到x轴的距离是3,则a=±6 D.若点A在第四象限,则a的值可以为﹣2
11.平面直角坐标系中,点A(﹣3,2),B(3,4),C(x,y),若AC∥x轴,则线段BC的最小值及此时点C的坐标分别为( )
A.6,(﹣3,4) B.2,(3,2) C.2,(3,0) D.1,(4,2)
12.已知点P(1,y),Q(x,2),若PQ∥x轴,且线段PQ=3,则x= ,y= .
13.已知点(a+1,2a+5)在y轴上,则该点坐标为 .
14.已知线段AB=4,AB∥x轴,若点A坐标为(﹣1,2),且点B在第一象限,则B点坐标为 .
15.在平面直角坐标系中,点A(﹣5,4)到y轴的距离是 ,点A关于x轴的对称点A′的坐标为 .
16.点P是第一象限内的点,若点P(2+a,3a+4)到x轴和y轴的距离相等,则点P的坐标为 .
17.若把点A(5m,2m﹣1)向上平移3个单位长度后,得到的点在x轴上,则点A的坐标为 .
18.已知平面直角坐标系中有一点M(m﹣1,2m+3)
(1)当m为何值时,点M到x轴的距离为1?
(2)当m为何值时,点M到y轴的距离为2?
19.如图,A(﹣1,0),C(1,4),点B在x轴上,且AB=3.
(1)求点B的坐标;
(2)求△ABC的面积;
(3)在y轴上是否存在点P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请直接写出点P的坐标;若不存在,请说明理由.
20.在4×4的正方形网格中建立如图1、2所示的直角坐标系,其中格点A,B的坐标分别是(0,1),(﹣1,﹣1).(1)请图1中添加一个格点C,使得△ABC是轴对称图形,且对称轴经过点(0,﹣1).
(2)请图2中添加一个格点D,使得△ABD也是轴对称图形,且对称轴经过点(1,1).
21.已知:A(0,1),B(2,0),C(4,3)
(1)在坐标系中描出各点,画出△ABC.
(2)求△ABC的面积;
(3)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.
22.在平面直角坐标系中,△ABC经过平移得到三角形△A'B'C',位置如图所示:
(1)分别写出点A、A'的坐标:A ,A' ;
(2)若点M(a,b)是△ABC内部一点,则平移后对应点M'的坐标为 ;
(3)求△ABC的面积.
参考答案
1.解:点A(﹣3,5)关于x轴对称的点的坐标为(﹣3,﹣5),
故选:B.
2.解:∵点A(m+2,3)与点B(﹣4,n+5)关于y轴对称,
∴m+2=4,n+5=3,
解得m=2,n=﹣2,
∴m+n=2﹣2=0.
故选:B.
3.解:A.根据点的坐标的特点,(4,﹣5)到x轴距离是5,且在第四象限,故A不符合题意.
B.根据点的坐标的特点,(﹣4,5)到x轴距离是5,且在第二象限,故B不符合题意.
C.根据点的坐标的特点,(﹣5,4)到x轴距离是4,且在第二象限,故C不符合题意.
D.根据点的坐标的特点,(5,﹣4)到x轴距离是4,且在第四象限,故D符合题意.
故选:D.
4.解:平移后点A的坐标为(﹣1+2,﹣3+3),即A(1,0),
故选:B.
5.解:根据题意可建立如图所示的平面直角坐标系:
则棋子“炮”的坐标为(2,1),
故选:B.
6.解:∵A(4,2),B(﹣2,2),
∴点A到x轴的距离为2,点B到x轴的距离为2,且A、B都在x轴上方,
∴AB平行于x轴,
故选:A.
7.解:∵点A的坐标是(3,a),将点A向下平移4个单位得到点A',
∴A'的坐标为(3,a﹣4),
∵点A与点A'关于x轴对称,
∴a+a﹣4=0,
解得:a=2.
故选:B.
8.解:A、点P(3,2)到x轴的距离是2,故本选项不符合题意.
B、若ab=0,则点P(a,b)表示原点或坐标轴上的点,故本选项不符合题意.
C、若A(2,﹣2)、B(2,2),则直线AB∥y轴,故本选项不符合题意.
D、第三象限内点的坐标,横纵坐标都是负号,故本选项符合题意.
故选:D.
9.解:第二象限内的点横坐标小于0,纵坐标大于0;
到x轴的距离是6,说明其纵坐标为6,到y轴的距离为5,说明其横坐标为﹣5,
因而点P的坐标是(﹣5,6).
故选:C.
10.解:A.若点A在y轴上,则a+1=0,解得a=﹣1,故本选项错误;
B.若点A在一三象限角平分线上,则a+1=3﹣a,解得a=1,故本选项正确;
C.若点A到x轴的距离是3,则|3﹣a|=3,解得a=6或0,故本选项错误;
D.若点A在第四象限,则a+1>0,且3﹣a<0,解得a>3,故a的值不可以为﹣2;
故选:B.
11.解:如图所示:
由垂线段最短可知:当BC⊥AC时,BC有最小值.
∴点C的坐标为(3,2),线段的最小值为2.
故选:B.
12.解:∵P(1,y),Q(x,2),且PQ∥x轴,
∴y=2,
又∵PQ=3,
∴|x﹣1|=3
∴x=4或﹣2,
故答案为:4或﹣2,2.
13.解:∵点(a+1,2a+5)在y轴上,
∴a+1=0,
解得:a=﹣1,
∴2a+5=3,
∴该点坐标为:(0,3).
故答案为:(0,3).
14.解:∵AB∥x轴,点A坐标为(﹣1,2),
∴A、B两点纵坐标都为2,
又∵AB=4,且点B在第一象限,点A坐标为(﹣1,2),
∴B点在A点右边,B(3,2).
故答案为:(3,2).
15.解:根据坐标的定义可知,
点A(﹣5,4)到y轴的距离是|﹣5|=5,
由关于x轴的对称点坐标之间的关系可得,
点A关于x轴的对称点A′的坐标为(﹣5,﹣4),
故答案为:5,(﹣5,﹣4).
16.解:∵点P是第一象限内的点,点P(2+a,3a+4)到x轴和y轴的距离相等,
∴2+a=3a+4,
解得a=﹣1,
∴点P的坐标为(1,1),
故答案为(1,1).
17.解:∵把点A(5m,2m﹣1)向上平移3个单位后得到的点在x轴上,
∴2m﹣1+3=0,
解得m=﹣1,
∴点A坐标为(﹣5,﹣3),
故答案为:(﹣5,﹣3).
18.解:(1)∵|2m+3|=1
2m+3=1或2m+3=﹣1
∴m=﹣1或m=﹣2;
(2)∵|m﹣1|=2
m﹣1=2或m﹣1=﹣2
∴m=3或m=﹣1.
19.解:(1)点B在点A的右边时,﹣1+3=2,
点B在点A的左边时,﹣1﹣3=﹣4,
所以,B的坐标为(2,0)或(﹣4,0);
(2)△ABC的面积=×3×4=6;
(3)设点P到x轴的距离为h,
则×3h=10,
解得h=,
点P在y轴正半轴时,P(0,),
点P在y轴负半轴时,P(0,﹣),
综上所述,点P的坐标为(0,)或(0,﹣).
20.解:(1)如图,点C即为所求.
(2)如图,点D即为所求.
21.解:(1)如图所示:
(2)过点C向x、y轴作垂线,垂足为D、E.
∴四边形DOEC的面积=3×4=12,△BCD的面积==3,△ACE的面积==4,△AOB的面积==1.
∴△ABC的面积=四边形DOEC的面积﹣△ACE的面积﹣△BCD的面积﹣△AOB的面积
=12﹣3﹣4﹣1=4.
(3)当点p在x轴上时,△ABP的面积==4,即:,解得:BP=8,
所以点P的坐标为(10,0)或(﹣6,0);
当点P在y轴上时,△ABP的面积==4,即,解得:AP=4.
所以点P的坐标为(0,5)或(0,﹣3).
所以点P的坐标为(0,5)或(0,﹣3)或(10,0)或(﹣6,0).
22.解:(1)观察图象可知,A(1,0),A′(﹣4,4),
故答案为:(1,0),(﹣4,4);
(2)∵△ABC向左平移5个单位,向上平移4个单位得到△A′B′C′.
∴M(a,b),平移后的坐标为(a﹣5,b+4),
故答案为:(a﹣5,b+4);
(3)S△ABC=4×4﹣×2×4﹣×1×4﹣×2×3=7.
