2021-2022学年华东师大版七年级数学上册第5章相交线与平行线 期末综合复习训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大版七年级数学上册第5章相交线与平行线 期末综合复习训练(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 386.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-05 20:33:35 | ||
图片预览


文档简介
2021-2022学年华师大版七年级数学上册《第5章相交线与平行线》
期末综合复习训练(附答案)
1.如图,a∥b,点B在直线b上,且AB⊥BC,若∠1=34°,则∠2的大小为( )
A.34° B.54° C.56° D.66°
2.如图,直线AB、CD相交于点O,∠DOF=90°,OF平分∠AOE,若∠BOD=32°,则∠EOF的度数为( )
A.32° B.48° C.58° D.64°
3.如图,如果AB∥CD,CD∥EF,那么∠BCE等于( )
A.∠1+∠2 B.∠2﹣∠1 C.180°﹣∠2+∠1 D.180°﹣∠1+∠2
4.点P为直线l外一点,点A、B、C为直线l上的三点,PA=2cm,PB=3cm,PC=4cm,那么点P到直线l的距离是( )
A.2cm B.小于2cm
C.不大于2cm D.大于2cm,且小于5cm
5.如图,直线a∥b,直角三角形如图放置,∠DCB=90°,若∠1+∠B=65°,则∠2的度数为( )
A.20° B.25° C.30° D.35°
6.下列命题中,是真命题的是( )
A.过一点有且只有一条直线与已知直线平行
B.相等的角是对顶角
C.两条直线被第三条直线所截,同旁内角互补
D.在同一平面内,垂直于同一直线的两条直线平行
7.下列图形中,线段AD的长表示点A到直线BC距离的是( )
A. B.
C. D.
8.如图,DH∥EG∥BC,且DC∥EF,那么图中和∠1相等的角有( )个.
A.2 B.4 C.5 D.6
9.如图,AB∥CD,有图中α,β,γ三角之间的关系是( )
A.α+β+γ=180° B.α﹣β+γ=180° C.α+β﹣γ=180° D.α+β+γ=360°
10.将一副三角板的直角顶点重合按如图所示方式放置,其中BC∥AE,则∠ACD的度数为( )
A.20° B.25° C.30° D.35°
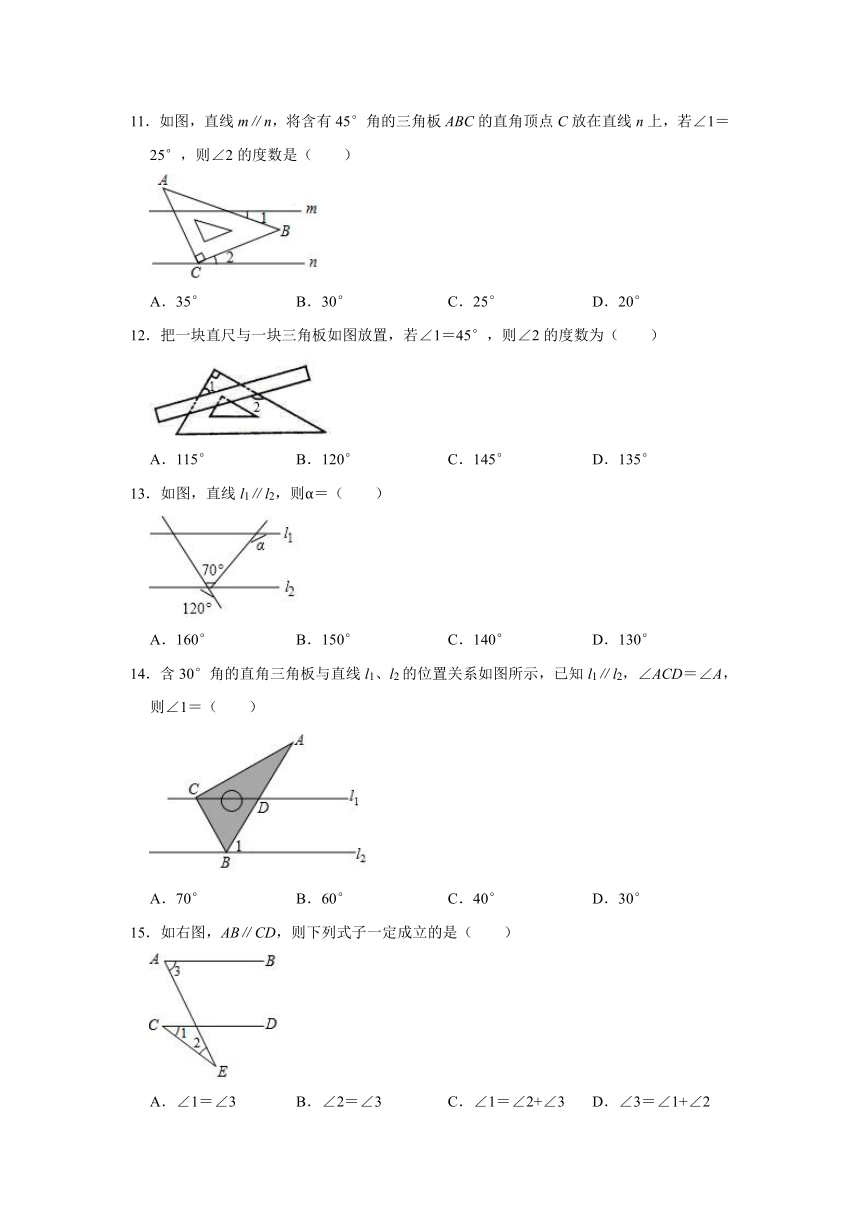
11.如图,直线m∥n,将含有45°角的三角板ABC的直角顶点C放在直线n上,若∠1=25°,则∠2的度数是( )
A.35° B.30° C.25° D.20°
12.把一块直尺与一块三角板如图放置,若∠1=45°,则∠2的度数为( )
A.115° B.120° C.145° D.135°
13.如图,直线l1∥l2,则α=( )
A.160° B.150° C.140° D.130°
14.含30°角的直角三角板与直线l1、l2的位置关系如图所示,已知l1∥l2,∠ACD=∠A,则∠1=( )
A.70° B.60° C.40° D.30°
15.如右图,AB∥CD,则下列式子一定成立的是( )
A.∠1=∠3 B.∠2=∠3 C.∠1=∠2+∠3 D.∠3=∠1+∠2
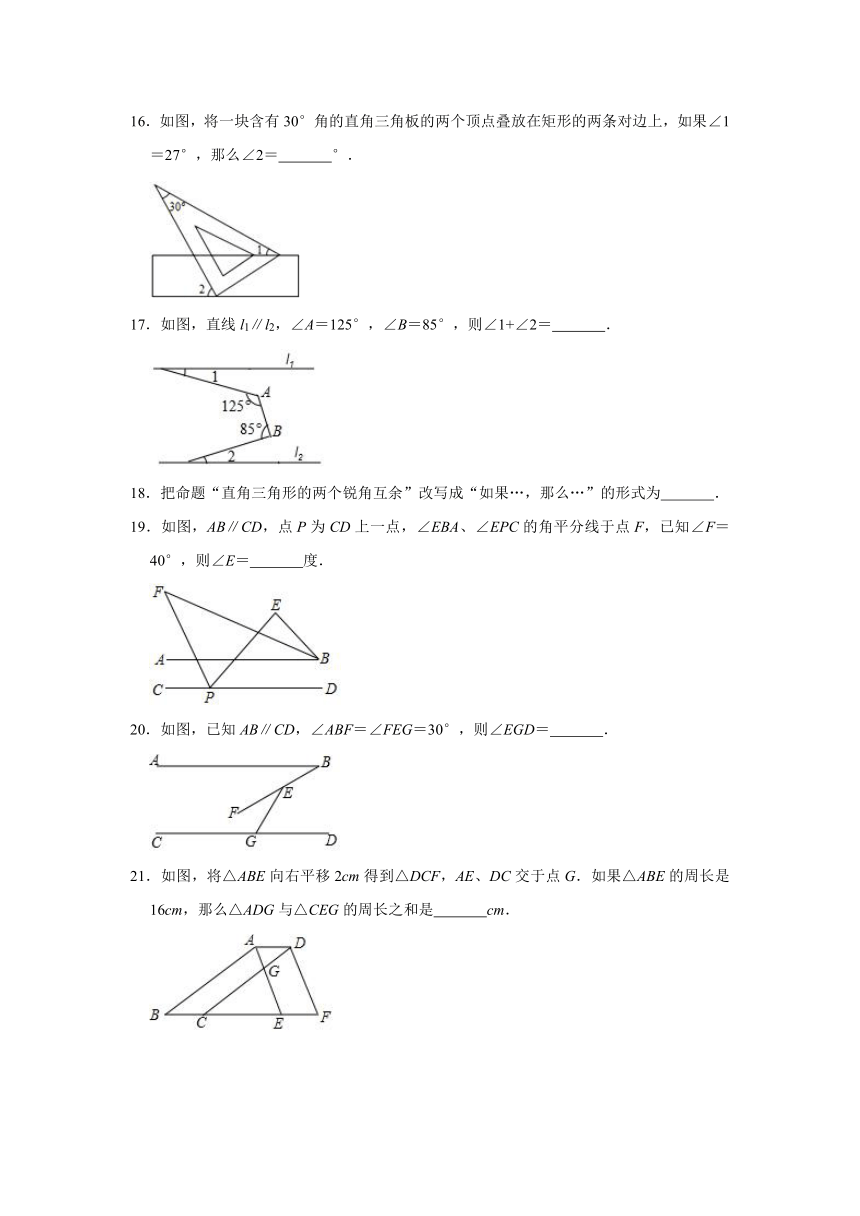
16.如图,将一块含有30°角的直角三角板的两个顶点叠放在矩形的两条对边上,如果∠1=27°,那么∠2= °.
17.如图,直线l1∥l2,∠A=125°,∠B=85°,则∠1+∠2= .
18.把命题“直角三角形的两个锐角互余”改写成“如果…,那么…”的形式为 .
19.如图,AB∥CD,点P为CD上一点,∠EBA、∠EPC的角平分线于点F,已知∠F=40°,则∠E= 度.
20.如图,已知AB∥CD,∠ABF=∠FEG=30°,则∠EGD= .
21.如图,将△ABE向右平移2cm得到△DCF,AE、DC交于点G.如果△ABE的周长是16cm,那么△ADG与△CEG的周长之和是 cm.
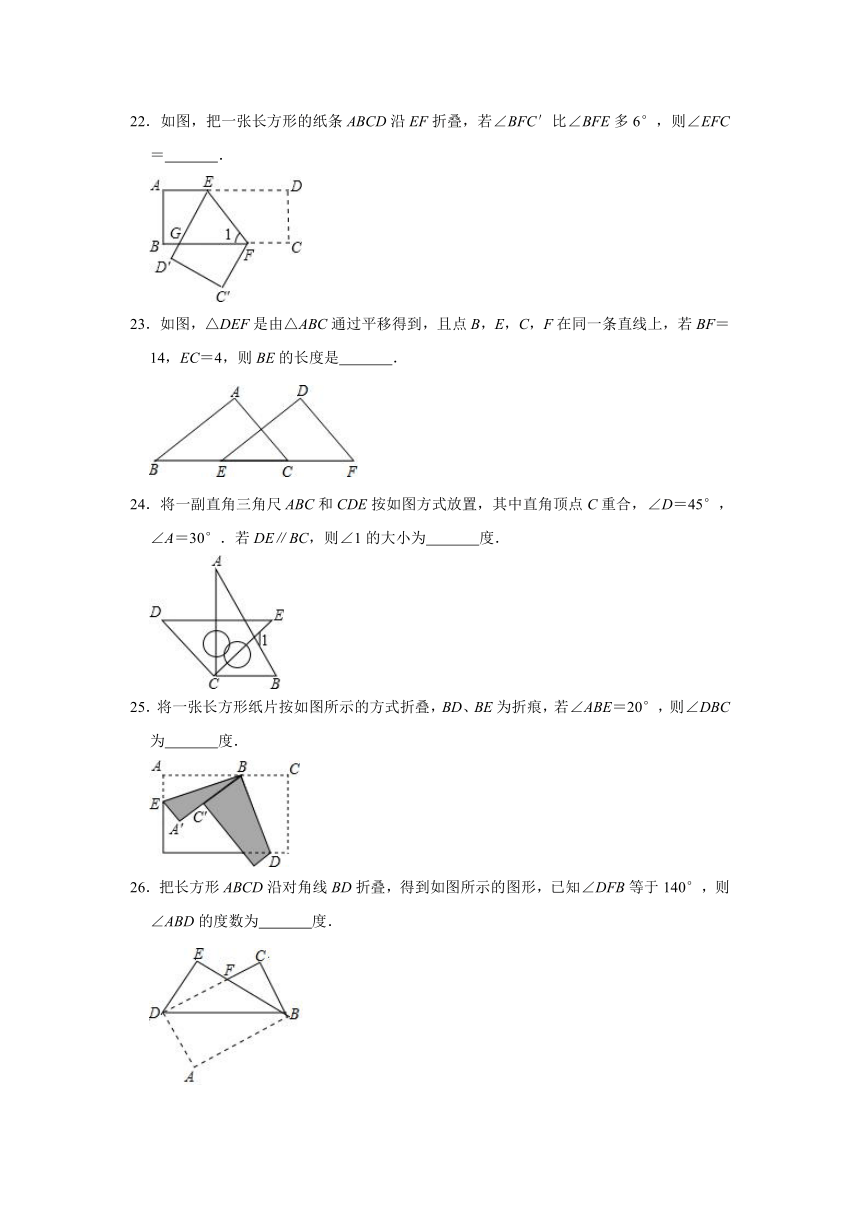
22.如图,把一张长方形的纸条ABCD沿EF折叠,若∠BFC′比∠BFE多6°,则∠EFC= .
23.如图,△DEF是由△ABC通过平移得到,且点B,E,C,F在同一条直线上,若BF=14,EC=4,则BE的长度是 .
24.将一副直角三角尺ABC和CDE按如图方式放置,其中直角顶点C重合,∠D=45°,∠A=30°.若DE∥BC,则∠1的大小为 度.
25.将一张长方形纸片按如图所示的方式折叠,BD、BE为折痕,若∠ABE=20°,则∠DBC为 度.
26.把长方形ABCD沿对角线BD折叠,得到如图所示的图形,已知∠DFB等于140°,则∠ABD的度数为 度.
27.将一直角三角板与两边平行的纸条如图所示放置,请你根据图示写出正确的信息或结论,要求至少写出两个,你写出的是 .
28.如图,把一张长方形ABCD的纸片沿EF折叠后,ED与BC的交点G,点D,C分别落在D′,C′的位置上,若∠EFG=55°,则∠GFC′= °.
29.如图,已知l1∥l2,直线l与l1、l2相交于C、D两点,把一块含30°角的三角尺按如图位置摆放.若∠1=130°,则∠2= .
30.将一副三角尺按如图所示方式摆放,若斜边DF∥AB,则∠1的度数为 .
31.如图,O为直线AB上一点,OC⊥OD.已知∠AOC的度数比∠BOD的度数的2倍多6°.
(1)求∠BOD的度数.
(2)若OE平分∠BOD,OF平分∠BOC,求∠EOF的度数.
32.完成下面的证明:
如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,连接DE,DF,DE∥AB,∠BFD=∠CED,连接BE交DF于点G,求证:∠EGF+∠AEG=180°.
证明:∵DE∥AB(已知),
∴∠A=∠CED( )
又∵∠BFD=∠CED(已知),
∴∠A=∠BFD( )
∴DF∥AE( )
∴∠EGF+∠AEG=180°( )
33.如图,直线AB∥CD,并且被直线MN所截,MN分别交AB和CD于点E与F,点Q在PM上,且∠EPM=∠FQM,求证:∠DFQ=∠BEP.
34.如图,已知∠1+∠2=180°,∠B=∠3,判断∠C与∠AED的大小关系,并说明理由.
35.已知,如图,AB∥CD,BD平分∠ABC,CE平分∠DCF,∠ACE=90°
(1)判断BD和CE的位置关系并说明理由;
(2)判断AC和BD是否垂直并说明理由.
36.已知:点A在射线CE上,∠C=∠D.
(1)如图1,若AC∥BD,求证:AD∥BC;
(2)如图2,若∠BAC=∠BAD,BD⊥BC,请探究∠DAE与∠C的数量关系,写出你的探究结论,并加以证明;
(3)如图3,在(2)的条件下,过点D作DF∥BC交射线于点F,当∠DFE=8∠DAE时,求∠BAD的度数.
38.如图1,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.
(1)探究猜想:①∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③猜想图1中∠AED、∠EAB、∠EDC的关系并说明理由.
(2)拓展应用,如图2,线段FE与长方形ABCD的边AB交于点E,与边CD 交于点F.图2中①②分别是被线段FE隔开的2个区域(不含边界),P是位于以上两个区域内的一点,猜想∠PEB,∠PFC,∠EPF的关系(不要求说明理由)
参考答案
1.解:∵a∥b,
∴∠1=∠3=34°,
又∵AB⊥BC,
∴∠2=90°﹣34°=56°,
故选:C.
2.解:∵∠DOF=90°,∠BOD=32°,
∴∠AOF=90°﹣32°=58°,
∵OF平分∠AOE,
∴∠AOF=∠EOF=58°.
故选:C.
3.解:∵AB∥CD,CD∥EF.
∴∠BCD=∠1,∠ECD=180°﹣∠2.
∴∠BCE=180°﹣∠2+∠1.
故选:C.
4.解:因为垂线段最短,
所以点P到直线l的距离为不大于2cm.
故选:C.
5.解:由三角形的外角性质可得,∠3=∠1+∠B=65°,
∵a∥b,∠DCB=90°,
∴∠2=180°﹣∠3﹣90°=180°﹣65°﹣90°=25°.
故选:B.
6.解:A、过直线外一点有且只有一条直线与已知直线平行,所以A选项错误;
B、相等的角不一定为对顶角,所以B选项错误;
C、两条平行直线被第三条直线所截,同旁内角互补,所以C选项错误;
D、在同一平面内,垂直于同一直线的两条直线平行,所以D选项正确.
故选:D.
7.解:线段AD的长表示点A到直线BC距离的是图D,
故选:D.
8.解:根据两直线平行,同位角相等、内错角相等,与∠1相等的角有:
∠2、∠3、∠4、∠5、∠6共5个.
故选:C.
9.解:如图,延长AE交直线CD于F,
∵AB∥CD,
∴∠α+∠AFD=180°,
∵∠AFD=∠β﹣∠γ,
∴∠α+∠β﹣∠γ=180°,
故选:C.
10.解:∵BC∥AE,
∴∠BCE=∠E=30°,
又∵∠BCD=90°=∠ACE,
∴∠ACD=∠BCE=30°,
故选:C.
11.解:过点B作BD∥l,
∵直线l∥m,
∴BD∥l∥m,
∴∠4=∠1=25°,
∵∠ABC=45°,
∴∠3=∠ABC﹣∠4=45°﹣25°=20°,
∴∠2=∠3=20°.
故选:D.
12.解:在Rt△ABC中,∠A=90°,
∵∠1=45°(已知),
∴∠3=90°﹣∠1=45°(三角形的内角和定理),
∴∠4=180°﹣∠3=135°(平角定义),
∵EF∥MN(已知),
∴∠2=∠4=135°(两直线平行,同位角相等).
故选:D.
13.解:如图,∵∠β=180°﹣120°=60°,
∴∠ACB=60°+70°=130°,
∵直线l1∥l2,
∴∠α=∠ACB=130°,
故选:D.
14.解:∵∠ACD=∠A=30°,
∴∠CDB=∠A+∠ACD=60°,
∵l1∥l2,
∴∠1=∠CDB=60°,
故选:B.
15.解:∵AB∥CD,
∴∠DFE=∠3,
∵∠DEF=∠1+∠2,
∴∠3=∠1+∠2.
故选:D.
16.解:∵将一块含有30°角的直角三角板的两个顶点叠放在矩形的两条对边上,∠1=27°,
∴∠4=90°﹣30°﹣27°=33°,
∵AD∥BC,
∴∠3=∠4=33°,
∴∠2=180°﹣90°﹣33°=57°,
故答案为:57°.
17.解:如图,
∵∠1+∠3=125°,∠2+∠4=85°,
∴∠1+∠3+∠2+∠4=210°,
∵l1∥l2,
∴∠3+∠4=180°,
∴∠1+∠2=210°﹣180°=30°.
故答案为30°.
18.解:如果一个三角形是直角三角形,那么它的两个锐角互余.
19.解:设∠EPC=2x,∠EBA=2y,
∵∠EBA、∠EPC的角平分线交于点F
∴∠CPF=∠EPF=x,∠EBF=∠FBA=y,
∵∠1=∠F+∠ABF=40°+y,
∠2=∠EBA+∠E=2y+∠E,
∵AB∥CD,
∴∠1=∠CPF=x,∠2=∠EPC=2x,
∴∠2=2∠1,
∴2y+∠E=2(40°+y),
∴∠E=80°.
故答案为:80.
20.解:过点E作EM∥AB,
∵AB∥CD,
∴EM∥CD,
∴∠ABF=∠BEM,
∴∠EGD+∠GEM=180°,
∵∠ABF=∠FEG=30°,
∴∠BEM=30°,
∵∠BEM+∠GEM+∠FEG=180°,
∴∠EGD=∠BEM+∠FEG=30°+30°=60°;
故答案为:60°.
21.解:∵△ABE向右平移2cm得到△DCF,
∴DF=AE,
∴△ADG与△CEG的周长之和=AD+CE+CD+AE=BE+AB+AE=16,
故答案为:16;
22.解:设∠EFC=x,∠1=y,则∠BFC′=x﹣y,
∵∠BFC′比∠BFE多6°,
∴x﹣2y=6,
∵x+y=180°,
可得x=122°
故答案为122°.
23.解:∵△DEF是由△ABC通过平移得到,
∴BE=CF,
∴BE=(BF﹣EC),
∵BF=14,EC=4,
∴BE=(14﹣4)=5.故答案为:5
24.解:∵DE∥BC,
∴∠E=∠ECB=45°,
∴∠1=∠ECB+∠B=45°+60°=105°,故答案为:105
25.解:根据翻折的性质可知,∠ABE=∠A′BE,∠DBC=∠DBC′,
又∵∠ABE+∠A′BE+∠DBC+∠DBC′=180°,
∴∠ABE+∠DBC=90°,
又∵∠ABE=20°,
∴∠DBC=70°.故答案为:70.
26.解:∵四边形ABCD是矩形,
∴AB∥CD,
∴∠CDB=∠ABD,
∵△BDE是由△BDA翻折得到,
∴∠ABD=∠DBE,
∴∠FDB=∠FBD,
∵∠DFB=140°,
∴∠DBF=(180°﹣140°)=20°,
∴∠ABD=20°故答案为20.
27.解:∠1=∠2,∠5+∠4=180°,
理由是:
∵AB⊥CD,
∴∠1=∠2,∠5+∠4=180°,
故答案为:∠1=∠2,∠5+∠4=180°.
28.解:根据题意得:∠GEF=∠DEF,
∵AD∥BC,
∴∠DEF=∠EFG=55°,∠EGF+∠DEG=180°,
∴∠GEF=55°,
∴∠DEG=110°,
∴∠EGF=70°,
∵C'F∥D'E,
∴∠GFC'=70°.故答案为:70.
29.解:∵∠1=130°,
∴∠3=50°,
又∵l1∥l2,
∴∠BDC=50°,
又∵∠ADB=30°,
∴∠2=20°,故答案为:20°.
30.解:∵DF∥AB,
∴∠F=∠BEF=45°,
又∵∠1=∠BEF+∠B,
∴∠1=45°+30°=75°,
故答案为:75°.
31.解:(1)设∠BOD=x,则∠AOC=2x+6,
∵OC⊥OD
∴∠COD=90°.
∵∠AOC+∠COD+∠BOD=180°
∴2x+6+90+x=180°,
解得x=28,即:∠BOD=28°.
(2)∵OE平分∠BOD
∴∠BOE=∠BOD=14°,
∵OF平分∠BOC,
∴∠BOF=∠BOC=(90+28)=59°,
∴∠EOF=∠BOF﹣∠BOE=59°﹣14°=45°.
32.证明:∵DE∥AB(已知),
∴∠A=∠CED(两直线平行,同位角相等)
又∵∠BFD=∠CED(已知),
∴∠A=∠BFD(等量代换)
∴DF∥AE(同位角相等,两直线平行)
∴∠EGF+∠AEG=180°(两直线平行,同旁内角互补)
故答案为:两直线平行,同位角相等;等量代换;同位角相等,两直线平行;两直线平行,同旁内角互补.
33.证明:∵∠EPM=∠FQM,
∴FQ∥EP,
∴∠MFQ=∠MEP,
又∵AB∥CD,
∴∠MFD=∠MEB,
∴∠MFQ﹣∠MFD=∠MEP﹣∠MEB,
∴∠DFQ=∠BEP.
34.解:∠C=∠AED,理由是:
∵∠1+∠2=180°,∠1+∠EFD=180°,
∴∠2=∠EFD,
∴AB∥EF,
∴∠3=∠ADE,
∵∠B=∠3,
∴∠ADE=∠B,
∴DE∥BC,
∴∠C=∠AED.
35.解:(1)BD∥CE.
理由:∵AB∥CD,
∴∠ABC=∠DCF,
∴BD平分∠ABC,CE平分∠DCF,
∴∠2=∠ABC,∠4=∠DCF,
∴∠2=∠4,
∴BD∥CE(同位角相等,两直线平行);
(2)AC⊥BD,
理由:∵BD∥CE,
∴∠DGC+∠ACE=180°,
∵∠ACE=90°,
∴∠DGC=180°﹣90°=90°,
即AC⊥BD.
36.解:(1)如图1,∵AC∥BD,
∴∠DAE=∠D,
又∵∠C=∠D,
∴∠DAE=∠C,
∴AD∥BC;
(2)∠EAD+2∠C=90°.
证明:如图2,设CE与BD交点为G,
∵∠CGB是△ADG是外角,
∴∠CGB=∠D+∠DAE,
∵BD⊥BC,
∴∠CBD=90°,
∴△BCG中,∠CGB+∠C=90°,
∴∠D+∠DAE+∠C=90°,
又∵∠D=∠C,
∴2∠C+∠DAE=90°;
(3)如图3,设∠DAE=α,则∠DFE=8α,
∵∠DFE+∠AFD=180°,
∴∠AFD=180°﹣8α,
∵DF∥BC,
∴∠C=∠AFD=180°﹣8α,
又∵2∠C+∠DAE=90°,
∴2(180°﹣8α)+α=90°,
∴α=18°,
∴∠C=180°﹣8α=36°=∠ADB,
又∵∠C=∠BDA,∠BAC=∠BAD,
∴∠ABC=∠ABD=∠CBD=45°,
∴△ABD中,∠BAD=180°﹣45°﹣36°=99°.
38.解:(1)①过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∵∠A=30°,∠D=40°,
∴∠1=∠A=30°,∠2=∠D=40°,
∴∠AED=∠1+∠2=70°;
②过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∵∠A=20°,∠D=60°,
∴∠1=∠A=20°,∠2=∠D=60°,
∴∠AED=∠1+∠2=80°;
③猜想:∠AED=∠EAB+∠EDC.
理由:过点E作EF∥CD,
∵AB∥DC∴EF∥AB(平行于同一条直线的两直线平行),
∴∠1=∠EAB,∠2=∠EDC(两直线平行,内错角相等),
∴∠AED=∠1+∠2=∠EAB+∠EDC(等量代换).
(2)如图2,当点P在①区域时,
∵AB∥CD,
∴∠BEF+∠CFE=180°,
∴∠PEF+∠PFE=(∠PEB+∠PFC)﹣180°.
∵∠PEF+∠PFE+∠EPF=180°,
∴∠EPF=180°﹣(∠PEF+∠PFE)=180°﹣(∠PEB+∠PFC)+180°=360°﹣(∠PEB+∠PFC);
当点P在区域②时,如图3所示,
∵AB∥CD,
∴∠BEF+∠CFE=180°,
∵∠EPF+∠FEP+∠PFE=180°,
∴∠EPF=∠PEB+∠PFC.
期末综合复习训练(附答案)
1.如图,a∥b,点B在直线b上,且AB⊥BC,若∠1=34°,则∠2的大小为( )
A.34° B.54° C.56° D.66°
2.如图,直线AB、CD相交于点O,∠DOF=90°,OF平分∠AOE,若∠BOD=32°,则∠EOF的度数为( )
A.32° B.48° C.58° D.64°
3.如图,如果AB∥CD,CD∥EF,那么∠BCE等于( )
A.∠1+∠2 B.∠2﹣∠1 C.180°﹣∠2+∠1 D.180°﹣∠1+∠2
4.点P为直线l外一点,点A、B、C为直线l上的三点,PA=2cm,PB=3cm,PC=4cm,那么点P到直线l的距离是( )
A.2cm B.小于2cm
C.不大于2cm D.大于2cm,且小于5cm
5.如图,直线a∥b,直角三角形如图放置,∠DCB=90°,若∠1+∠B=65°,则∠2的度数为( )
A.20° B.25° C.30° D.35°
6.下列命题中,是真命题的是( )
A.过一点有且只有一条直线与已知直线平行
B.相等的角是对顶角
C.两条直线被第三条直线所截,同旁内角互补
D.在同一平面内,垂直于同一直线的两条直线平行
7.下列图形中,线段AD的长表示点A到直线BC距离的是( )
A. B.
C. D.
8.如图,DH∥EG∥BC,且DC∥EF,那么图中和∠1相等的角有( )个.
A.2 B.4 C.5 D.6
9.如图,AB∥CD,有图中α,β,γ三角之间的关系是( )
A.α+β+γ=180° B.α﹣β+γ=180° C.α+β﹣γ=180° D.α+β+γ=360°
10.将一副三角板的直角顶点重合按如图所示方式放置,其中BC∥AE,则∠ACD的度数为( )
A.20° B.25° C.30° D.35°
11.如图,直线m∥n,将含有45°角的三角板ABC的直角顶点C放在直线n上,若∠1=25°,则∠2的度数是( )
A.35° B.30° C.25° D.20°
12.把一块直尺与一块三角板如图放置,若∠1=45°,则∠2的度数为( )
A.115° B.120° C.145° D.135°
13.如图,直线l1∥l2,则α=( )
A.160° B.150° C.140° D.130°
14.含30°角的直角三角板与直线l1、l2的位置关系如图所示,已知l1∥l2,∠ACD=∠A,则∠1=( )
A.70° B.60° C.40° D.30°
15.如右图,AB∥CD,则下列式子一定成立的是( )
A.∠1=∠3 B.∠2=∠3 C.∠1=∠2+∠3 D.∠3=∠1+∠2
16.如图,将一块含有30°角的直角三角板的两个顶点叠放在矩形的两条对边上,如果∠1=27°,那么∠2= °.
17.如图,直线l1∥l2,∠A=125°,∠B=85°,则∠1+∠2= .
18.把命题“直角三角形的两个锐角互余”改写成“如果…,那么…”的形式为 .
19.如图,AB∥CD,点P为CD上一点,∠EBA、∠EPC的角平分线于点F,已知∠F=40°,则∠E= 度.
20.如图,已知AB∥CD,∠ABF=∠FEG=30°,则∠EGD= .
21.如图,将△ABE向右平移2cm得到△DCF,AE、DC交于点G.如果△ABE的周长是16cm,那么△ADG与△CEG的周长之和是 cm.
22.如图,把一张长方形的纸条ABCD沿EF折叠,若∠BFC′比∠BFE多6°,则∠EFC= .
23.如图,△DEF是由△ABC通过平移得到,且点B,E,C,F在同一条直线上,若BF=14,EC=4,则BE的长度是 .
24.将一副直角三角尺ABC和CDE按如图方式放置,其中直角顶点C重合,∠D=45°,∠A=30°.若DE∥BC,则∠1的大小为 度.
25.将一张长方形纸片按如图所示的方式折叠,BD、BE为折痕,若∠ABE=20°,则∠DBC为 度.
26.把长方形ABCD沿对角线BD折叠,得到如图所示的图形,已知∠DFB等于140°,则∠ABD的度数为 度.
27.将一直角三角板与两边平行的纸条如图所示放置,请你根据图示写出正确的信息或结论,要求至少写出两个,你写出的是 .
28.如图,把一张长方形ABCD的纸片沿EF折叠后,ED与BC的交点G,点D,C分别落在D′,C′的位置上,若∠EFG=55°,则∠GFC′= °.
29.如图,已知l1∥l2,直线l与l1、l2相交于C、D两点,把一块含30°角的三角尺按如图位置摆放.若∠1=130°,则∠2= .
30.将一副三角尺按如图所示方式摆放,若斜边DF∥AB,则∠1的度数为 .
31.如图,O为直线AB上一点,OC⊥OD.已知∠AOC的度数比∠BOD的度数的2倍多6°.
(1)求∠BOD的度数.
(2)若OE平分∠BOD,OF平分∠BOC,求∠EOF的度数.
32.完成下面的证明:
如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,连接DE,DF,DE∥AB,∠BFD=∠CED,连接BE交DF于点G,求证:∠EGF+∠AEG=180°.
证明:∵DE∥AB(已知),
∴∠A=∠CED( )
又∵∠BFD=∠CED(已知),
∴∠A=∠BFD( )
∴DF∥AE( )
∴∠EGF+∠AEG=180°( )
33.如图,直线AB∥CD,并且被直线MN所截,MN分别交AB和CD于点E与F,点Q在PM上,且∠EPM=∠FQM,求证:∠DFQ=∠BEP.
34.如图,已知∠1+∠2=180°,∠B=∠3,判断∠C与∠AED的大小关系,并说明理由.
35.已知,如图,AB∥CD,BD平分∠ABC,CE平分∠DCF,∠ACE=90°
(1)判断BD和CE的位置关系并说明理由;
(2)判断AC和BD是否垂直并说明理由.
36.已知:点A在射线CE上,∠C=∠D.
(1)如图1,若AC∥BD,求证:AD∥BC;
(2)如图2,若∠BAC=∠BAD,BD⊥BC,请探究∠DAE与∠C的数量关系,写出你的探究结论,并加以证明;
(3)如图3,在(2)的条件下,过点D作DF∥BC交射线于点F,当∠DFE=8∠DAE时,求∠BAD的度数.
38.如图1,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.
(1)探究猜想:①∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③猜想图1中∠AED、∠EAB、∠EDC的关系并说明理由.
(2)拓展应用,如图2,线段FE与长方形ABCD的边AB交于点E,与边CD 交于点F.图2中①②分别是被线段FE隔开的2个区域(不含边界),P是位于以上两个区域内的一点,猜想∠PEB,∠PFC,∠EPF的关系(不要求说明理由)
参考答案
1.解:∵a∥b,
∴∠1=∠3=34°,
又∵AB⊥BC,
∴∠2=90°﹣34°=56°,
故选:C.
2.解:∵∠DOF=90°,∠BOD=32°,
∴∠AOF=90°﹣32°=58°,
∵OF平分∠AOE,
∴∠AOF=∠EOF=58°.
故选:C.
3.解:∵AB∥CD,CD∥EF.
∴∠BCD=∠1,∠ECD=180°﹣∠2.
∴∠BCE=180°﹣∠2+∠1.
故选:C.
4.解:因为垂线段最短,
所以点P到直线l的距离为不大于2cm.
故选:C.
5.解:由三角形的外角性质可得,∠3=∠1+∠B=65°,
∵a∥b,∠DCB=90°,
∴∠2=180°﹣∠3﹣90°=180°﹣65°﹣90°=25°.
故选:B.
6.解:A、过直线外一点有且只有一条直线与已知直线平行,所以A选项错误;
B、相等的角不一定为对顶角,所以B选项错误;
C、两条平行直线被第三条直线所截,同旁内角互补,所以C选项错误;
D、在同一平面内,垂直于同一直线的两条直线平行,所以D选项正确.
故选:D.
7.解:线段AD的长表示点A到直线BC距离的是图D,
故选:D.
8.解:根据两直线平行,同位角相等、内错角相等,与∠1相等的角有:
∠2、∠3、∠4、∠5、∠6共5个.
故选:C.
9.解:如图,延长AE交直线CD于F,
∵AB∥CD,
∴∠α+∠AFD=180°,
∵∠AFD=∠β﹣∠γ,
∴∠α+∠β﹣∠γ=180°,
故选:C.
10.解:∵BC∥AE,
∴∠BCE=∠E=30°,
又∵∠BCD=90°=∠ACE,
∴∠ACD=∠BCE=30°,
故选:C.
11.解:过点B作BD∥l,
∵直线l∥m,
∴BD∥l∥m,
∴∠4=∠1=25°,
∵∠ABC=45°,
∴∠3=∠ABC﹣∠4=45°﹣25°=20°,
∴∠2=∠3=20°.
故选:D.
12.解:在Rt△ABC中,∠A=90°,
∵∠1=45°(已知),
∴∠3=90°﹣∠1=45°(三角形的内角和定理),
∴∠4=180°﹣∠3=135°(平角定义),
∵EF∥MN(已知),
∴∠2=∠4=135°(两直线平行,同位角相等).
故选:D.
13.解:如图,∵∠β=180°﹣120°=60°,
∴∠ACB=60°+70°=130°,
∵直线l1∥l2,
∴∠α=∠ACB=130°,
故选:D.
14.解:∵∠ACD=∠A=30°,
∴∠CDB=∠A+∠ACD=60°,
∵l1∥l2,
∴∠1=∠CDB=60°,
故选:B.
15.解:∵AB∥CD,
∴∠DFE=∠3,
∵∠DEF=∠1+∠2,
∴∠3=∠1+∠2.
故选:D.
16.解:∵将一块含有30°角的直角三角板的两个顶点叠放在矩形的两条对边上,∠1=27°,
∴∠4=90°﹣30°﹣27°=33°,
∵AD∥BC,
∴∠3=∠4=33°,
∴∠2=180°﹣90°﹣33°=57°,
故答案为:57°.
17.解:如图,
∵∠1+∠3=125°,∠2+∠4=85°,
∴∠1+∠3+∠2+∠4=210°,
∵l1∥l2,
∴∠3+∠4=180°,
∴∠1+∠2=210°﹣180°=30°.
故答案为30°.
18.解:如果一个三角形是直角三角形,那么它的两个锐角互余.
19.解:设∠EPC=2x,∠EBA=2y,
∵∠EBA、∠EPC的角平分线交于点F
∴∠CPF=∠EPF=x,∠EBF=∠FBA=y,
∵∠1=∠F+∠ABF=40°+y,
∠2=∠EBA+∠E=2y+∠E,
∵AB∥CD,
∴∠1=∠CPF=x,∠2=∠EPC=2x,
∴∠2=2∠1,
∴2y+∠E=2(40°+y),
∴∠E=80°.
故答案为:80.
20.解:过点E作EM∥AB,
∵AB∥CD,
∴EM∥CD,
∴∠ABF=∠BEM,
∴∠EGD+∠GEM=180°,
∵∠ABF=∠FEG=30°,
∴∠BEM=30°,
∵∠BEM+∠GEM+∠FEG=180°,
∴∠EGD=∠BEM+∠FEG=30°+30°=60°;
故答案为:60°.
21.解:∵△ABE向右平移2cm得到△DCF,
∴DF=AE,
∴△ADG与△CEG的周长之和=AD+CE+CD+AE=BE+AB+AE=16,
故答案为:16;
22.解:设∠EFC=x,∠1=y,则∠BFC′=x﹣y,
∵∠BFC′比∠BFE多6°,
∴x﹣2y=6,
∵x+y=180°,
可得x=122°
故答案为122°.
23.解:∵△DEF是由△ABC通过平移得到,
∴BE=CF,
∴BE=(BF﹣EC),
∵BF=14,EC=4,
∴BE=(14﹣4)=5.故答案为:5
24.解:∵DE∥BC,
∴∠E=∠ECB=45°,
∴∠1=∠ECB+∠B=45°+60°=105°,故答案为:105
25.解:根据翻折的性质可知,∠ABE=∠A′BE,∠DBC=∠DBC′,
又∵∠ABE+∠A′BE+∠DBC+∠DBC′=180°,
∴∠ABE+∠DBC=90°,
又∵∠ABE=20°,
∴∠DBC=70°.故答案为:70.
26.解:∵四边形ABCD是矩形,
∴AB∥CD,
∴∠CDB=∠ABD,
∵△BDE是由△BDA翻折得到,
∴∠ABD=∠DBE,
∴∠FDB=∠FBD,
∵∠DFB=140°,
∴∠DBF=(180°﹣140°)=20°,
∴∠ABD=20°故答案为20.
27.解:∠1=∠2,∠5+∠4=180°,
理由是:
∵AB⊥CD,
∴∠1=∠2,∠5+∠4=180°,
故答案为:∠1=∠2,∠5+∠4=180°.
28.解:根据题意得:∠GEF=∠DEF,
∵AD∥BC,
∴∠DEF=∠EFG=55°,∠EGF+∠DEG=180°,
∴∠GEF=55°,
∴∠DEG=110°,
∴∠EGF=70°,
∵C'F∥D'E,
∴∠GFC'=70°.故答案为:70.
29.解:∵∠1=130°,
∴∠3=50°,
又∵l1∥l2,
∴∠BDC=50°,
又∵∠ADB=30°,
∴∠2=20°,故答案为:20°.
30.解:∵DF∥AB,
∴∠F=∠BEF=45°,
又∵∠1=∠BEF+∠B,
∴∠1=45°+30°=75°,
故答案为:75°.
31.解:(1)设∠BOD=x,则∠AOC=2x+6,
∵OC⊥OD
∴∠COD=90°.
∵∠AOC+∠COD+∠BOD=180°
∴2x+6+90+x=180°,
解得x=28,即:∠BOD=28°.
(2)∵OE平分∠BOD
∴∠BOE=∠BOD=14°,
∵OF平分∠BOC,
∴∠BOF=∠BOC=(90+28)=59°,
∴∠EOF=∠BOF﹣∠BOE=59°﹣14°=45°.
32.证明:∵DE∥AB(已知),
∴∠A=∠CED(两直线平行,同位角相等)
又∵∠BFD=∠CED(已知),
∴∠A=∠BFD(等量代换)
∴DF∥AE(同位角相等,两直线平行)
∴∠EGF+∠AEG=180°(两直线平行,同旁内角互补)
故答案为:两直线平行,同位角相等;等量代换;同位角相等,两直线平行;两直线平行,同旁内角互补.
33.证明:∵∠EPM=∠FQM,
∴FQ∥EP,
∴∠MFQ=∠MEP,
又∵AB∥CD,
∴∠MFD=∠MEB,
∴∠MFQ﹣∠MFD=∠MEP﹣∠MEB,
∴∠DFQ=∠BEP.
34.解:∠C=∠AED,理由是:
∵∠1+∠2=180°,∠1+∠EFD=180°,
∴∠2=∠EFD,
∴AB∥EF,
∴∠3=∠ADE,
∵∠B=∠3,
∴∠ADE=∠B,
∴DE∥BC,
∴∠C=∠AED.
35.解:(1)BD∥CE.
理由:∵AB∥CD,
∴∠ABC=∠DCF,
∴BD平分∠ABC,CE平分∠DCF,
∴∠2=∠ABC,∠4=∠DCF,
∴∠2=∠4,
∴BD∥CE(同位角相等,两直线平行);
(2)AC⊥BD,
理由:∵BD∥CE,
∴∠DGC+∠ACE=180°,
∵∠ACE=90°,
∴∠DGC=180°﹣90°=90°,
即AC⊥BD.
36.解:(1)如图1,∵AC∥BD,
∴∠DAE=∠D,
又∵∠C=∠D,
∴∠DAE=∠C,
∴AD∥BC;
(2)∠EAD+2∠C=90°.
证明:如图2,设CE与BD交点为G,
∵∠CGB是△ADG是外角,
∴∠CGB=∠D+∠DAE,
∵BD⊥BC,
∴∠CBD=90°,
∴△BCG中,∠CGB+∠C=90°,
∴∠D+∠DAE+∠C=90°,
又∵∠D=∠C,
∴2∠C+∠DAE=90°;
(3)如图3,设∠DAE=α,则∠DFE=8α,
∵∠DFE+∠AFD=180°,
∴∠AFD=180°﹣8α,
∵DF∥BC,
∴∠C=∠AFD=180°﹣8α,
又∵2∠C+∠DAE=90°,
∴2(180°﹣8α)+α=90°,
∴α=18°,
∴∠C=180°﹣8α=36°=∠ADB,
又∵∠C=∠BDA,∠BAC=∠BAD,
∴∠ABC=∠ABD=∠CBD=45°,
∴△ABD中,∠BAD=180°﹣45°﹣36°=99°.
38.解:(1)①过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∵∠A=30°,∠D=40°,
∴∠1=∠A=30°,∠2=∠D=40°,
∴∠AED=∠1+∠2=70°;
②过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∵∠A=20°,∠D=60°,
∴∠1=∠A=20°,∠2=∠D=60°,
∴∠AED=∠1+∠2=80°;
③猜想:∠AED=∠EAB+∠EDC.
理由:过点E作EF∥CD,
∵AB∥DC∴EF∥AB(平行于同一条直线的两直线平行),
∴∠1=∠EAB,∠2=∠EDC(两直线平行,内错角相等),
∴∠AED=∠1+∠2=∠EAB+∠EDC(等量代换).
(2)如图2,当点P在①区域时,
∵AB∥CD,
∴∠BEF+∠CFE=180°,
∴∠PEF+∠PFE=(∠PEB+∠PFC)﹣180°.
∵∠PEF+∠PFE+∠EPF=180°,
∴∠EPF=180°﹣(∠PEF+∠PFE)=180°﹣(∠PEB+∠PFC)+180°=360°﹣(∠PEB+∠PFC);
当点P在区域②时,如图3所示,
∵AB∥CD,
∴∠BEF+∠CFE=180°,
∵∠EPF+∠FEP+∠PFE=180°,
∴∠EPF=∠PEB+∠PFC.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
