2021-2022学年华东师大版九年级数学上册第21章二次根式期末综合复习训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大版九年级数学上册第21章二次根式期末综合复习训练(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 307.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-05 20:40:54 | ||
图片预览
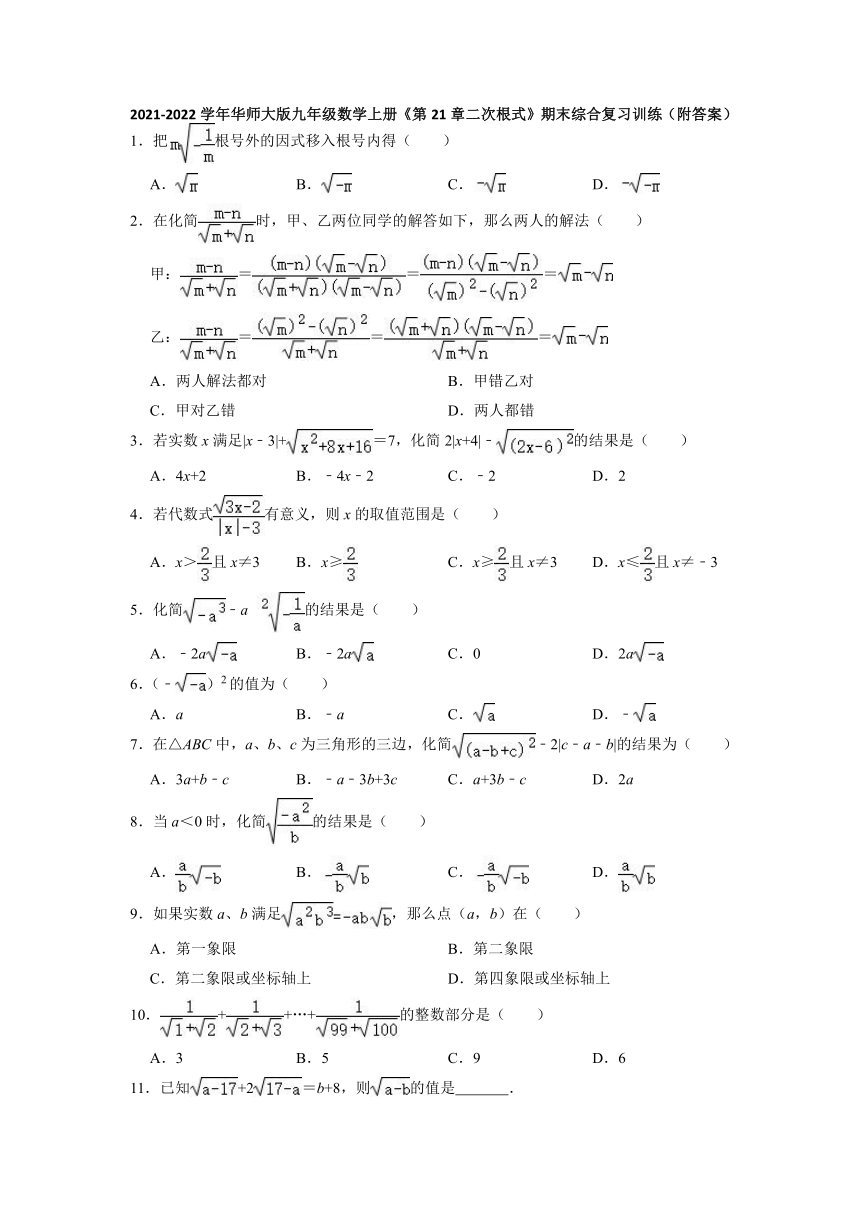



文档简介
2021-2022学年华师大版九年级数学上册《第21章二次根式》期末综合复习训练(附答案)
1.把根号外的因式移入根号内得( )
A. B. C. D.
2.在化简时,甲、乙两位同学的解答如下,那么两人的解法( )
甲:===
乙:===
A.两人解法都对 B.甲错乙对
C.甲对乙错 D.两人都错
3.若实数x满足|x﹣3|+=7,化简2|x+4|﹣的结果是( )
A.4x+2 B.﹣4x﹣2 C.﹣2 D.2
4.若代数式有意义,则x的取值范围是( )
A.x>且x≠3 B.x≥ C.x≥且x≠3 D.x≤且x≠﹣3
5.化简﹣a的结果是( )
A.﹣2a B.﹣2a C.0 D.2a
6.(﹣)2的值为( )
A.a B.﹣a C. D.﹣
7.在△ABC中,a、b、c为三角形的三边,化简﹣2|c﹣a﹣b|的结果为( )
A.3a+b﹣c B.﹣a﹣3b+3c C.a+3b﹣c D.2a
8.当a<0时,化简的结果是( )
A. B. C. D.
9.如果实数a、b满足,那么点(a,b)在( )
A.第一象限 B.第二象限
C.第二象限或坐标轴上 D.第四象限或坐标轴上
10.++…+的整数部分是( )
A.3 B.5 C.9 D.6
11.已知+2=b+8,则的值是 .
12.若最简根式和可以合并,则a b的值是 .
13.若a=1,b=1﹣,则代数式的值为
14.如图,在长方形内有两个相邻的正方形A,B,正方形A的面积为2,正方形B的面积为4,则图中阴影部分的面积是 .
15.计算:()2022()2021= .
16.当﹣1<a<0时,则= .
17.计算= .
18.已知是整数,则满足条件的最小正整数n为 .
19.已知:m+n=10,mn=9,则= .
20.化简:2<x<4时,﹣= .
21.计算:
(1)﹣
(2)(+3)(3﹣)﹣(﹣1)2
22.已知a=,求的值.
23.(1)9÷×
(2)﹣2﹣2÷2﹣2+﹣1﹣(﹣1)0
(3)(π﹣1)0+()﹣1+|5﹣|﹣
(4)(2+3)2021(2﹣3)222﹣4﹣
24.已知x=,y=,求:(1)x2y﹣xy2的值;(2)x2﹣xy+y2的值.
25.计算:+﹣3﹣.
参考答案
1.解:∵成立,
∴﹣>0,即m<0,
∴原式=﹣=﹣.
故选:D.
2.解:甲同学在计算时,将分子和分母都乘以(﹣),而﹣是有可能等于0,此时变形后分式没有意义,
所以甲同学的解法错误;
乙同学的解法正确;
故选:B.
3.解:∵|x﹣3|+=7,
∴|x﹣3|+|x+4|=7,
∴﹣4≤x≤3,
∴2|x+4|﹣
=2(x+4)﹣|2x﹣6|
=2(x+4)﹣(6﹣2x)
=4x+2,
故选:A.
4.解:∵代数式有意义,
∴3x﹣2≥0,|x|﹣3≠0,
解得:x≥且x≠3.
故选:C.
5.解:﹣a
=﹣a﹣a2
=﹣a+a
=0.
故选:C.
6.解:∵有意义,
∴a≤0,
∴(﹣)2=﹣a.
故选:B.
7.解:∵a、b、c为三角形的三边,
∴a+c>b,a+b>c,
即a﹣b+c>0,c﹣a﹣b<0;
∴﹣2|c﹣a﹣b|=(a﹣b+c)+2(c﹣a﹣b)=﹣a﹣3b+3c.
故选:B.
8.解:根据a<0,
∴===,
故选:A.
9.解:∵实数a、b满足,
∴a、b异号,且b>0;
故a<0,或者a、b中有一个为0或均为0.
于是点(a,b)在第二象限或坐标轴上.故选C.
解:原式=+…+
=++…+
=++…+
=++…+
=﹣1
=﹣1+10
=9.故选C.
11.解:由题可得,
解得,
即a=17,
∴0=b+8,
∴b=﹣8,
∴==5,
故答案为:5.
12.解:∵最简根式和可以合并∴,
解得:,
∴a b=18,
故答案为:18.
13.解:∵a=1,b=1﹣,
∴a﹣b=2,ab=﹣1,
∴
=
=
=3,
故答案为:3.
14.解:设两个正方形A,B的边长是x、y(x<y),
则x2=2,y2=4,
x=,y=2,
则阴影部分的面积是(y﹣x)x=(2﹣)×=2﹣2,
故答案为:2﹣2.
15.解:()2022()2021
=[()()]2021 ()
=(﹣1)2021 ()
=﹣﹣,
故答案为:﹣﹣.
16.解:∵﹣1<a<0,
∴a+<0,a﹣>0,
原式=﹣
=a﹣+a+
=2a,
故答案为:2a.
17.解:原式===﹣1,
故答案为:﹣1.
18.解:∵==2,且是整数;
∴2是整数,即5n是完全平方数;
∴n的最小正整数值为5.
故答案是:5.
19.解:∵m+n=10,mn=9,
∴()2
=
=
=
=,
∴=±.
故答案是:.
20.解:∵2<x<4,
∴x﹣2>0,x﹣4<0,
∴原式=﹣
=|x﹣2|﹣|x﹣4|
=x﹣2﹣(4﹣x)
=x﹣2﹣4+x
=2x﹣6.
故答案为:2x﹣6.
21.解:(1)原式=﹣
=2﹣﹣
=2﹣;
(2)原式=32﹣()2﹣(3﹣2+1)
=9﹣5﹣4+2
=2.
22.解:∵a===2﹣,
∴a﹣2=2﹣﹣2=﹣<0,
则原式=﹣
=a+3+
=2﹣+3+2+
=7.
23.解:(1)9÷×
=
=
=54;
(2)﹣2﹣2÷2﹣2+﹣1﹣(﹣1)0
=3﹣1+﹣1﹣1
=4﹣3;
(3)(π﹣1)0+()﹣1+|5﹣|﹣
=1++3﹣5﹣8
=﹣12+;
(4)(2+3)2021(2﹣3)2022﹣4﹣
=[(2+3)(2﹣3)]2021×(2﹣3)﹣﹣(﹣1)
=(8﹣9)2021×(2﹣3)﹣﹣+1
=(﹣1)2021×(2﹣3)﹣﹣+1
=﹣(2﹣3)﹣﹣+1
=﹣2+3﹣﹣+1
=﹣4+4.
24.解:∵x===3+2,y===3﹣2,
∴xy==1,x+y=3+2+3﹣2=6,
∴(1)x2y﹣xy2,
=xy(x﹣y),
=1×,
=4;
(2)x2﹣xy+y2,
=(x+y)2﹣3xy,
=62﹣3×1,
=36﹣3,
=33.
25.解:原式=2+﹣3×﹣
=2+﹣﹣3+3
=﹣2+.
1.把根号外的因式移入根号内得( )
A. B. C. D.
2.在化简时,甲、乙两位同学的解答如下,那么两人的解法( )
甲:===
乙:===
A.两人解法都对 B.甲错乙对
C.甲对乙错 D.两人都错
3.若实数x满足|x﹣3|+=7,化简2|x+4|﹣的结果是( )
A.4x+2 B.﹣4x﹣2 C.﹣2 D.2
4.若代数式有意义,则x的取值范围是( )
A.x>且x≠3 B.x≥ C.x≥且x≠3 D.x≤且x≠﹣3
5.化简﹣a的结果是( )
A.﹣2a B.﹣2a C.0 D.2a
6.(﹣)2的值为( )
A.a B.﹣a C. D.﹣
7.在△ABC中,a、b、c为三角形的三边,化简﹣2|c﹣a﹣b|的结果为( )
A.3a+b﹣c B.﹣a﹣3b+3c C.a+3b﹣c D.2a
8.当a<0时,化简的结果是( )
A. B. C. D.
9.如果实数a、b满足,那么点(a,b)在( )
A.第一象限 B.第二象限
C.第二象限或坐标轴上 D.第四象限或坐标轴上
10.++…+的整数部分是( )
A.3 B.5 C.9 D.6
11.已知+2=b+8,则的值是 .
12.若最简根式和可以合并,则a b的值是 .
13.若a=1,b=1﹣,则代数式的值为
14.如图,在长方形内有两个相邻的正方形A,B,正方形A的面积为2,正方形B的面积为4,则图中阴影部分的面积是 .
15.计算:()2022()2021= .
16.当﹣1<a<0时,则= .
17.计算= .
18.已知是整数,则满足条件的最小正整数n为 .
19.已知:m+n=10,mn=9,则= .
20.化简:2<x<4时,﹣= .
21.计算:
(1)﹣
(2)(+3)(3﹣)﹣(﹣1)2
22.已知a=,求的值.
23.(1)9÷×
(2)﹣2﹣2÷2﹣2+﹣1﹣(﹣1)0
(3)(π﹣1)0+()﹣1+|5﹣|﹣
(4)(2+3)2021(2﹣3)222﹣4﹣
24.已知x=,y=,求:(1)x2y﹣xy2的值;(2)x2﹣xy+y2的值.
25.计算:+﹣3﹣.
参考答案
1.解:∵成立,
∴﹣>0,即m<0,
∴原式=﹣=﹣.
故选:D.
2.解:甲同学在计算时,将分子和分母都乘以(﹣),而﹣是有可能等于0,此时变形后分式没有意义,
所以甲同学的解法错误;
乙同学的解法正确;
故选:B.
3.解:∵|x﹣3|+=7,
∴|x﹣3|+|x+4|=7,
∴﹣4≤x≤3,
∴2|x+4|﹣
=2(x+4)﹣|2x﹣6|
=2(x+4)﹣(6﹣2x)
=4x+2,
故选:A.
4.解:∵代数式有意义,
∴3x﹣2≥0,|x|﹣3≠0,
解得:x≥且x≠3.
故选:C.
5.解:﹣a
=﹣a﹣a2
=﹣a+a
=0.
故选:C.
6.解:∵有意义,
∴a≤0,
∴(﹣)2=﹣a.
故选:B.
7.解:∵a、b、c为三角形的三边,
∴a+c>b,a+b>c,
即a﹣b+c>0,c﹣a﹣b<0;
∴﹣2|c﹣a﹣b|=(a﹣b+c)+2(c﹣a﹣b)=﹣a﹣3b+3c.
故选:B.
8.解:根据a<0,
∴===,
故选:A.
9.解:∵实数a、b满足,
∴a、b异号,且b>0;
故a<0,或者a、b中有一个为0或均为0.
于是点(a,b)在第二象限或坐标轴上.故选C.
解:原式=+…+
=++…+
=++…+
=++…+
=﹣1
=﹣1+10
=9.故选C.
11.解:由题可得,
解得,
即a=17,
∴0=b+8,
∴b=﹣8,
∴==5,
故答案为:5.
12.解:∵最简根式和可以合并∴,
解得:,
∴a b=18,
故答案为:18.
13.解:∵a=1,b=1﹣,
∴a﹣b=2,ab=﹣1,
∴
=
=
=3,
故答案为:3.
14.解:设两个正方形A,B的边长是x、y(x<y),
则x2=2,y2=4,
x=,y=2,
则阴影部分的面积是(y﹣x)x=(2﹣)×=2﹣2,
故答案为:2﹣2.
15.解:()2022()2021
=[()()]2021 ()
=(﹣1)2021 ()
=﹣﹣,
故答案为:﹣﹣.
16.解:∵﹣1<a<0,
∴a+<0,a﹣>0,
原式=﹣
=a﹣+a+
=2a,
故答案为:2a.
17.解:原式===﹣1,
故答案为:﹣1.
18.解:∵==2,且是整数;
∴2是整数,即5n是完全平方数;
∴n的最小正整数值为5.
故答案是:5.
19.解:∵m+n=10,mn=9,
∴()2
=
=
=
=,
∴=±.
故答案是:.
20.解:∵2<x<4,
∴x﹣2>0,x﹣4<0,
∴原式=﹣
=|x﹣2|﹣|x﹣4|
=x﹣2﹣(4﹣x)
=x﹣2﹣4+x
=2x﹣6.
故答案为:2x﹣6.
21.解:(1)原式=﹣
=2﹣﹣
=2﹣;
(2)原式=32﹣()2﹣(3﹣2+1)
=9﹣5﹣4+2
=2.
22.解:∵a===2﹣,
∴a﹣2=2﹣﹣2=﹣<0,
则原式=﹣
=a+3+
=2﹣+3+2+
=7.
23.解:(1)9÷×
=
=
=54;
(2)﹣2﹣2÷2﹣2+﹣1﹣(﹣1)0
=3﹣1+﹣1﹣1
=4﹣3;
(3)(π﹣1)0+()﹣1+|5﹣|﹣
=1++3﹣5﹣8
=﹣12+;
(4)(2+3)2021(2﹣3)2022﹣4﹣
=[(2+3)(2﹣3)]2021×(2﹣3)﹣﹣(﹣1)
=(8﹣9)2021×(2﹣3)﹣﹣+1
=(﹣1)2021×(2﹣3)﹣﹣+1
=﹣(2﹣3)﹣﹣+1
=﹣2+3﹣﹣+1
=﹣4+4.
24.解:∵x===3+2,y===3﹣2,
∴xy==1,x+y=3+2+3﹣2=6,
∴(1)x2y﹣xy2,
=xy(x﹣y),
=1×,
=4;
(2)x2﹣xy+y2,
=(x+y)2﹣3xy,
=62﹣3×1,
=36﹣3,
=33.
25.解:原式=2+﹣3×﹣
=2+﹣﹣3+3
=﹣2+.
